高一数学必修4课件：1-2-1单位圆中的三角函数线
合集下载
人教版高中数学数学必修四1.2.1+单位圆与三角函数线第一课时+教案
第二学期高一教案主备人：使用人：时间：1.单位圆的概念有向线段的概念用正弦线、余弦线、正切线表示任意角的三角函数值一、知识目标知识目标：1.说出单位圆的概念2.说出有向线段的概念3.用正弦线、余弦线、正切线表示任意角的三角函数值二、能力目标：正确利用与单位圆有关的有向线段，将任意角α的正弦、余弦、正切函数值表示出来，即用正弦线、余弦线、正切线表示出来，经历知识产生的过程，培养分析问题、解决问题的能力。
精美句子1、善思则能“从无字句处读书”。
读沙漠，读出了它坦荡豪放的胸怀；读太阳，读出了它普照万物的无私；读春雨，读出了它润物无声的柔情。
读大海，读出了它气势磅礴的豪情。
读石灰，读出了它粉身碎骨不变色的清白。
2、幸福幸福是“临行密密缝，意恐迟迟归”的牵挂；幸福是“春种一粒粟，秋收千颗子”的收获. 幸福是“采菊东篱下，悠然见南山”的闲适；幸福是“奇闻共欣赏，疑义相与析”的愉悦。
幸福是“随风潜入夜，润物细无声”的奉献；幸福是“夜来风雨声，花落知多少”的恬淡。
幸福是“零落成泥碾作尘，只有香如故”的圣洁。
幸福是“壮志饥餐胡虏肉，笑谈渴饮匈奴血”的豪壮。
幸福是“先天下之忧而忧，后天下之乐而乐”的胸怀。
幸福是“人生自古谁无死，留取丹心照汗青”的气节。
3、大自然的语言丰富多彩：从秋叶的飘零中，我们读出了季节的变换；从归雁的行列中，我读出了集体的力量；从冰雪的消融中，我们读出了春天的脚步；从穿石的滴水中，我们读出了坚持的可贵；从蜂蜜的浓香中，我们读出了勤劳的甜美。
4、成功与失败种子，如果害怕埋没，那它永远不能发芽。
鲜花，如果害怕凋谢，那它永远不能开放。
矿石，如果害怕焚烧（熔炉），那它永远不能成钢（炼成金子）。
蜡烛，如果害怕熄灭（燃烧），那它永远不能发光。
航船，如果害怕风浪，那它永远不能到达彼岸。
5、墙角的花，当你孤芳自赏时，天地便小了。
井底的蛙，当你自我欢唱时，视野便窄了。
笼中的鸟，当你安于供养时，自由便没了。
山中的石！当你背靠群峰时，意志就坚了。
人教B版高中数学必修四《1.2.2 单位圆与三角函数线》课件
的终边 叫做单位圆．
P cxo,sy ,sin cos
x
x, sin
y
y
x MA1, 0
r
r
P cos,sin
三角函数定义：
角 的余弦和正弦分别等于角的终
边与c单os位圆交O点M的横s坐in标和纵O坐N标
在结任论意：角向 的量终O边M上，,M任OPN取分一点别P叫做x,y的(原余点弦除外线)，和点正P弦到原线
切线变成了一点，它的数量为零． tan 0
②当角 的终边在y轴上时，正切线不存在．
例2 作出 2 的正切线
3
2
y
的终边
3
解：在直角坐标系中作单位圆如图，以 Ox 轴
正方向为始边作
2 3
的终边，由单位圆与
Ox
o
正方向的交点 A 作 Ox 轴的垂线与 OP 的反
2
向延长线交于T 点，则 tan 3
角 的终边在坐标轴上的情况： ①当角 的终边在x轴上时，点P与点M重合，这时正弦线变成 了一点，它的数量为零，而余弦线的数量OM=1或-1 ．
sin 0,cos 1或 1
②当角 的终边在y轴上时，正弦线的数量MP=1或-1，余弦线 变成了一点，它表示的数量为零．
sin 1或 1,cos 0
，余弦线为 OM
MP OM
反馈练习：分别作出 和- 3 的正弦线和余弦线
并比较其数量的大小。3 4
tan y y
x
x, y x 1 1, y
的终边 y
1,tan
T 1,tan T1,tan
o
tan AT或AT
1.2.1(2)单位圆与三角函数线(高中数学人教A版必修四).ppt
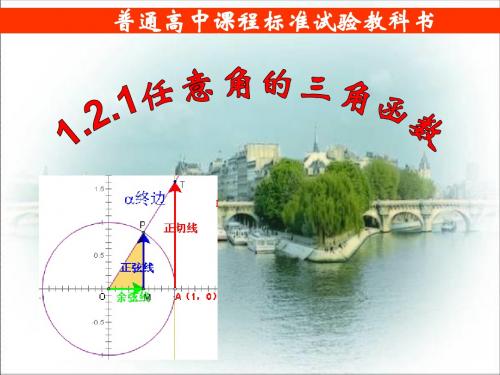
π 5π (2)如图所示，在 0～2π 内作出正切值等于 1 的角：4和 4 ， 则在图中所示的阴影区域内的每个角 x(不包括终边在 y 轴上的 角)均满足 tanx≤1.
π 5π π 所以所求的角 x 的集合为： {x|2kπ＋2<x≤ 4 ＋2kπ 或－2＋ π π π 2kπ<x≤4＋2kπ，k∈Z}＝{x|kπ－2<x≤kπ＋4，k∈Z}．
cos OM tan AT
O P
A(1,0)
α的终边
终边落在第四象限
y
α
sin MP
M A(1,0)
O
P
T
x
cos OM tan AT
α的终边
α的终边 y P α
M
三角函数线
y α的终边 P T x
A(1,0) T
α
O y
O
M A(1,0)
x
sin MP cos OM
3. 特殊情况： ① 当角的终边在x轴上时，点P与点M重合， 点T与点A重合，这时正弦线与正切线都变成 了一点，数量为零，而余弦线OM=1或－1。 ② 当角的终边在y轴上时，正弦线MP=1或－1 余弦线变成了一点，它表示的数量为零，正切 线不存在。
用 途
三角函数线的具体作用 :
1.比较两个三角函数值的大小
实例
剖析
3π 例1、作出 2π 的正弦线、余弦线和正切线.. 4 3
解：在直角坐标系中作单位圆如图示 2
y y
以x轴的正半轴为始边作出 的角， 3 其终边与单位圆交于P点，作PM x轴，垂足
为M，由单位圆与x轴的正半轴的交点A作 x轴的垂线, 与OP的反向延长线交于T点，
P
2021版高中数学人教A必修4课件：1.2.1.2 三角函数线
M 第2课时 三角函数线
目标导航
UBIAODAOHANG
Z 知识梳理 HISHI SHULI
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
【做一做1】 如图,P是角α的终边与单位圆的交点,PM⊥x轴于
M,AT和A'T'均是单位圆的切线,则角α的( )
A.正弦线是PM,正切线是A'T' B.正弦线是MP,正切线是A'T' C.正弦线是MP,正切线是AT D.正弦线是PM,正切线是AT 答案:C
-7-
M 第2课时 三角函数线
目标导航
UBIAODAOHANG
Z 知识梳理 HISHI SHULI
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
三角函数线的应用 剖析:三角函数线是三角函数值的直观表达形式,从三角函数线
的方向可以看出三角函数值的符号,从三角函数线的长度可以看出 三角函数值的绝对值的大小.三角函数线的主要作用是解三角方程 和不等式、证明三角不等式、求函数的定义域及其比较大小,同时 它也是以后画三角函数图象的基础.
-13-
M 第2课时 三角函数线
目标导航
UBIAODAOHANG
Z 知识梳理 HISHI SHULI
题型一 题型二 题型三
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
-14-
M 第2课时 三角函数线
目标导航
UBIAODAOHANG
Z 知识梳理 HISHI SHULI
题型一 题型二 题型三
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
高中数学 1.2.2《单位圆与三角函数线》(1) 新人教B版必修4
ppt课件
练习
1.函数y=
| sin x | sin x
+ cos x
|cos x |
+
|
ta n ta n
x x
| 的值域是
(
C
)
(A) {－1，1}
(B) {－1，1，3}
(C) {－1，3}
(D) {1，3}
ppt课件
2.已知角θ的终边上有一点P(－4a, 3a)(a≠0),则
2sinθ+cosθ的值是 ( C)
证明：sinα=|ON|=|MP|,
α= AP
tanα=|AT|.
y
N
PT
x
又 S扇形OAPSOAT
O
MA
所以 1OA1OAAT
2
2
即sinα<α<tanα .
ppt课件
小结： 1. 给定任意一个角α，都能在单位圆中作出它
的正弦线、余弦线、正切线。 2. 三角函数线的位置 ： 正弦线为从原点到α的终边与单位圆的交点
在y轴上的射影的有向线段； 余弦线为从原点到α的终边与单位圆的交点
在x轴上的射影的有向线段； 正切线在过单位圆与x轴正方向的交点的切 线上，为有向线段 A T
ppt课件
3. 特殊情况： ① 当角的终边在x轴上时，点P与点M重合， 点T与点A重合，这时正弦线与正切线都变成 了一点，数量为零，而余弦线OM=1或－1。 ② 当角的终边在y轴上时，正弦线MP=1或－1 余弦线变成了一点，它表示的数量为零，正切 线不存在。
sin y 5 解得y=－1.
4 y2
5
所以cosθ= － 2 5 . 5
ppt课件
x
其反向延长线)相交于点
练习
1.函数y=
| sin x | sin x
+ cos x
|cos x |
+
|
ta n ta n
x x
| 的值域是
(
C
)
(A) {－1，1}
(B) {－1，1，3}
(C) {－1，3}
(D) {1，3}
ppt课件
2.已知角θ的终边上有一点P(－4a, 3a)(a≠0),则
2sinθ+cosθ的值是 ( C)
证明：sinα=|ON|=|MP|,
α= AP
tanα=|AT|.
y
N
PT
x
又 S扇形OAPSOAT
O
MA
所以 1OA1OAAT
2
2
即sinα<α<tanα .
ppt课件
小结： 1. 给定任意一个角α，都能在单位圆中作出它
的正弦线、余弦线、正切线。 2. 三角函数线的位置 ： 正弦线为从原点到α的终边与单位圆的交点
在y轴上的射影的有向线段； 余弦线为从原点到α的终边与单位圆的交点
在x轴上的射影的有向线段； 正切线在过单位圆与x轴正方向的交点的切 线上，为有向线段 A T
ppt课件
3. 特殊情况： ① 当角的终边在x轴上时，点P与点M重合， 点T与点A重合，这时正弦线与正切线都变成 了一点，数量为零，而余弦线OM=1或－1。 ② 当角的终边在y轴上时，正弦线MP=1或－1 余弦线变成了一点，它表示的数量为零，正切 线不存在。
sin y 5 解得y=－1.
4 y2
5
所以cosθ= － 2 5 . 5
ppt课件
x
其反向延长线)相交于点
高中数学第一单元基本初等函数Ⅱ1.2.2单位圆与三角函数线课件新人教B版必修4
跟踪训练2 比较sin 1 155°与sin(－1 654°)的大小. 解 sin 1 155°＝sin(3×360°＋75°)＝sin 75°，
sin(－1 654°)＝sin(－5×360°＋146°)＝sin 146°.
如图，在单位圆中，分别作出sin 75°和sin 146°的
正弦线M1P1，M2P2.
思考2
点的射影是如何定义的？ 答案 过点P作PM垂直x轴于点M，作PN垂直于y轴于点N，
则点M，N分别是点P在x轴、y轴上的正射影(简称射影).
答案
梳理
(1)单位圆 把 半径为1 的圆叫做单位圆. (2)单位圆中角α的坐标 角α的余弦和正弦分别等于角α终边与单位圆交点的 横坐标 和 纵坐标 .
知识点二
第一章 §1.2
任意角的三角函数
1.2.2 单位圆与三角函数线
学习目标
1. 了解三角函数线的意义，能用三角函数线表示一个
角的正弦、余弦和正切.
2.能利用三角函数线解决一些简单的三角函数问题.
内容索引
问题导学
题型探究 当堂训练
问题导学
Байду номын сангаас
知识点一
单位圆
思考1
什么叫单位圆？
答案 把半径为1的圆叫做单位圆.
1 1 解 已知角 α 的正弦值，可知 MP＝2，则 P 点纵坐标为2. 1 所以在 y 轴上取点0，2 过该点作 x 轴的平行线， 交单位圆于 P1， P2 两点， ，
则OP1，OP2是角α的终边，
π 因而角 α 的取值集合为{α|α＝2kπ＋6或 5π α＝2kπ＋ 6 ，k∈Z}.
1 解 作直线x＝－ 交单位圆于C，D两点， 2 连接OC与OD，
2019版数学人教B版必修4课件：1.2.2 单位圆与三角函数线 .pdf
点分别为A(1,0),A'(-1,0),而与y轴的交点分别为B(0,1),B'(0,-1).
设角α的顶点在圆心O,始边与x轴的正半轴重合,终边与单位圆相
交于点P(如图①),过点P作PM垂直x轴于点M,作PN垂直y轴于点N,
则点M,N分别是点P在x轴、y轴上的正射影(简称射影).由三角函数 的定义可知,点P的坐标为(cos α,sin α),即P(cos α,sin α).其中cos α
=OM,sin α=ON.
-4-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
12
这就是说,角α的余弦和正弦分别等于角α终边与单位圆交点的横 坐标和纵坐标.
1.2.2 单位圆与三角函数线
-1-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
1.会利用单位圆中的有向线段表示正弦、余弦和正切. 2.能使用三角函数线求三角函数值、比较大小、解简单的三角 方程或三角不等式、证明相关的命题等.
答案:B
-3-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
设角α的顶点在圆心O,始边与x轴的正半轴重合,终边与单位圆相
交于点P(如图①),过点P作PM垂直x轴于点M,作PN垂直y轴于点N,
则点M,N分别是点P在x轴、y轴上的正射影(简称射影).由三角函数 的定义可知,点P的坐标为(cos α,sin α),即P(cos α,sin α).其中cos α
=OM,sin α=ON.
-4-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
12
这就是说,角α的余弦和正弦分别等于角α终边与单位圆交点的横 坐标和纵坐标.
1.2.2 单位圆与三角函数线
-1-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
1.会利用单位圆中的有向线段表示正弦、余弦和正切. 2.能使用三角函数线求三角函数值、比较大小、解简单的三角 方程或三角不等式、证明相关的命题等.
答案:B
-3-
M Z Z 1.2.2 单位圆与三角函数线
目标导航
UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
高中数学人教B版必修四课件：1.2.2单位圆与三角函数线
如在数轴上，|OA|=3，|OB|=3
OA 3 OB 3
x
B
O
A
3. 三角函数线
设任意角α的顶点
在原点，始边与x轴的
正半轴重合，终边与 单位圆相交于点P(x， A'(-1,0)
B(0,1) y
P(cos,sin) N1
x
O M A(1,0)
y），过P作x轴的垂线， 垂足为M； 做PN垂直
66
6
sin p < p < t an p
44
4
sin p < p < t an p
33
3
你有什么一般猜想？ sin a < a < tan a
思考：对于不等式 sin a < a < tan a
（其中α 为锐角），你能用数形结合思想证明吗？
yT P
O M Ax
探究：当0＜α＜π/2时，总有 sinα＜α＜tanα.
我们首先建立下面的坐标系：
在观览车转轮圆面所在的平面
y
内，以观览车转轮中心为原点， P
以水平线为x轴，以转轮半径为
x
单位长建立直角坐标系。
MO
设P 点为转轮边缘上的一点, 它表示座椅的位置，记 xOP ，则由正弦函数的定义可知，
MP sin
1.单位圆的概念
一般地，我们把半径为1的圆叫做单位圆，
4
变式： 写出满足条件 1 ≤cosα＜
2
23的角α
的集合.
2
y
3
1
6
-1 O
4
-1
3
1
x
11
6
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
新课引入
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
摩天轮是一种大型转轮状的机械建筑设施，上面挂在轮 边缘的是供乘客乘搭的座舱．乘客坐在摩天轮上慢慢往上 转，可以从高处俯瞰四周景色．假设摩天轮的中心离地面的 高度为h，它的直径为2R，逆时针方向匀速转动，转动一周需 360秒． 若你坐在座舱中，从水平位置向上开始转动，经过30秒 后，你离地面的高度为多少？
π 11π 值范围为6＋2kπ， 6 ＋2kπ(k∈Z)．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
π 3π － ＝tan ＝－1，且 (2)∵tan 4 4
tanθ>－1，
π π 3π ∴由图所示 θ 的取值范围为－ ＋2kπ， ＋2kπ∪ ＋2kπ， 4 2 4 3π π π ＋2kπ＝－4＋nπ，2＋nπ(k∈Z，n∈Z)． 2
π 5 6和6π.在图中所示的阴影区域内的每一个角 x，其正弦值都满 1 1 5π 13 足 sinx≤2，所以不等式 sinx≤2的解集为：{x| 6 ＋2kπ≤x≤ 6 π ＋2kπ，k∈Z}．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
π 5π (2)如图所示，在 0～2π 内作出正切值等于 1 的角：4和 4 ， 则在图中所示的阴影区域内的每个角 x(不包括终边在 y 轴上的 角)均满足 tanx≤1.
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
温故知新 1．角α的终边经过P(2,3)，则有( 2 13 A．sinα＝ 13 3 13 C．sinα＝ 13
[答案] C
[解析] sinα＝ 由三角函数的定义可知，r＝ 22＋32 ＝ 13 .∴
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
π 7 1 π 7 (3)由于 sin(－ )＝sin π＝－ ， 则在坐标系中画出－ 和 π， 6 6 2 6 6 确定 α 的终边位置．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
1 如图所示， 作直线 y＝－2交单位圆于 A、 两点， B 则∠xOA 7π π ＝ 6 ，∠xOB＝－6.过在直线 AB 上方的圆弧上任一点 P 作 PM ⊥x 轴于 M，则 MP＝sinα. 则 α 的终边不能与直线 AB 下方的圆弧有交点，则有 2kπ π 7π －6≤α≤2kπ＋ 6 (k∈Z)． π 7 即原不等式的解集是{α|2kπ－ ≤α≤2kπ＋ π，k∈Z}． 6 6
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
过点P作x轴的垂线PM，垂足为M，过点A作单位圆的切 线交OP的延长线(或反向延长线)于T点，这样就有sinα＝ MP ， cosα＝ OM ，tanα＝ AT ．单位圆中的有向线段MP、OM、AT 分别叫做角α的 正弦 线、 余弦 线、 正切 线，统称为三角函 数线．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
4．若750° 角的终边上有一点(4，a)，则a的值是_____．
[答案]
4 3 － 3
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
[解析]
∵tan750° ＝tan(360° ×2＋30° )
3 a ＝tan30° ＝ ＝ . 3 4 3 4 3 ∴a＝ 3 ×(4)＝ 3 .
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
命题方向
利用三角函数线解三角不等式
[例 2] 围：
利用单位圆， 求使下列不等式成立的 x 的取值范
1 2 (1)sinx≤2；(2)tanx≤1；(3)cosx≥ 2 .
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
[解析]
1 (1)如图所示，在 0～2π 内作出正弦值等于2的角：
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
[点评]
3 (1)中 cosθ＝ 2 对应的角 θ 的两条终边 OA、OB，
3 使 cosθ< 2 成立的角 θ 的终边所在区域为图中阴影部分，由逆 π 11π π 时针旋转角变大知，OA 取6时，OB 应取 6 而不是－6，这是 3 极易出错的地方，若改为 cosθ> 2 ，则角 θ 终边所在区域应为
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
如图所示，P是角α的终边与单位圆的交点，PM⊥x轴于 M，AT和A′T′均是单位圆的切线，则角α的( )
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
A．正弦线是PM，正切线是A′T′ B．正弦线是MP，正切线是A′T′ C．正弦线是MP，正切线是AT D．正弦线是PM，正切线是AT
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
解方程：tanα＝－1.
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
[解析]
因为角 α 的正切值等于－1，所以 AT＝－1.在单位
圆上过点 A(1,0)的切线与直线 y＝－1 交于点 T，连接 OT，OT 所在直线与单位圆交于 P1、P2 两点 OP1、OP2 是角 α 的终边， 3π 7 则角 α 的取值集合是{α|α＝2kπ＋ 4 或 α＝2kπ＋4π， k∈Z}＝{α|α 3π ＝nπ＋ 4 ，n∈Z}，如图.
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
π 5π π 所以所求的角 x 的集合为： {x|2kπ＋2<x≤ 4 ＋2kπ 或－2＋ π π π 2kπ<x≤4＋2kπ，k∈Z}＝{x|kπ－2<x≤kπ＋4，k∈Z}．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
2 π 7π (3)如图所示，在 0～2π 内作出余弦值等于 2 的角：4和 4 ， 2 则在图中所示的阴影区域内的每个角 x 均满足 cosx≥ 2 .所以 2 满足 cosx≥ 2 的角的集合为： π π {x|2kπ－ ≤x≤2kπ＋ ，k∈Z}． 4 4
1 已知角 α 的正弦值，可知 MP＝ ，则 P 点纵坐标 2
1 1 1 为2.所以在 y 轴上取点(0，2)，过这点作 x 轴的平行线 y＝2， 交单位圆于 P1、P2 两点，则 OP1、OP2 是角 α 的终边，因而角 π 5π α 的集合为{α|α＝2kπ＋6或 α＝2kπ＋ 6 ，k∈Z}，如图：
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
规律总结：利用三角函数线求解 sinα＝a 这样的三角方 程时，只需作直线 y＝a 与单位圆相交，连接原点和交点所得 射线即为所求角 α 的终边位置．求解 cosα＝a 这样的三角方程 时，需作直线 x＝a 与单位圆相交，连接原点和交点所得射线 即为所求角 α 的终边．求解 tanα＝a 这样的三角方程时，需作 直线 y＝a 与过点 A(1,0)的单位圆的切线 AT 相交，交点为 T， 连接原点 O 与交点 T，直线 OT 就是所求角 α 的终边位置．
成才之路· 数学
人教学 ·人教A版 · 必修4
第一章
1.2 任意角的三角函数
第一章 三角函数
成才之路 ·数学 ·人教A版 · 必修4
第一章
1．2.1 单位圆中的三角函数线
第一章 三角函数
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习 随堂应用练习 思路方法技巧 课后强化作业 名师辨误做答
)
13 B．cosα＝ 2 2 D．tanα＝3
3 3 13 ＝ 13 ，故选C. 13
第一章 1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
25π 2．sin 6 等于( 1 A.2 1 C．－ 2
[答案] A
) 3 B. 2 3 D．－ 2
[解析]
25π π π 1 由诱导公式(可知)sin 6 ＝sin(4π＋6)＝sin6＝2.
[答案]
D
第一章 1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
思路方法技巧
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
命题方向
利用三角函数线解三角方程
[例 1]
1 已知 sinα＝ ，求出角 α 的取值集合． 2
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
[解析]
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
3．在下列各式中填上适当的不等号： (1)sin759° 28′8″________0； (2)sin(－759° 23′8″)________0； 13 (3)tan(－ 5 π)________0； 41 (4)cos π________0. 7
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4
自主预习 认真阅读教材P15～17回答下列问题． 三角函数线 (1)有向线段：带有方向 的线段叫做有向线段． (2)定义：如图，设单位圆与x轴的正半轴交于点A，与角α 的终边交于点P(角α的顶点与原点重合，角α的始边与x轴的非 负半轴重合)．
第一章
1.2 .1
成才之路 ·数学 ·人教A版 · 必修4