单球面折射成像公式及其应用_张家乐
1-3傍轴条件下的单球面折射成像资料

y ' ns ' #
y n's
f ' n' ,代入 #式,得 fn
f x'
x f'
2)
tan(u) h u Q
s
y
n
l -u
tan(u) h u s
P -s
代入#式,得:
y y
nu n u
-i A n’
h -i’ l’
d
u’
O rC
P’ -y’
s’
Q’
拉格朗日—亥姆霍兹不变式
y' y
P Q C ∽ P Q C , yP C s r
y P Cr s
由 物 像 公 式 n ' n n ' n , 变 形 得 : s r n s
s ' s r
s r n s
y' ns' #
y n's
12
1)利用s ( f x),s' ( f ' x'), 牛顿公式xx' ff ',
焦物距x:物方焦点到物点的距离
焦象距x':象方焦点到象点的距离
n -x -f
•P F• -s
n'
f'
x' P’
F• ' •
s'
f f 1 s s
根据上面的定义, 有:s=x+f , s'=x'+f '
代入高斯公式,得
f ' f 1
f 'x' f x
整理得 xx'ff' ---牛顿公式(普适公式)
1-3傍轴条件下的单球面折 射成像
单球面折射成像公式及其应用_张家乐

v =8.0cm 所 成的像点的位置在A 点正上方8.0cm 处,即
B 点正上方16.0cm 处.
— 53 —
2016年第3期 物理通报 竞赛与物理专题研修
(2)当容器内装满折射 率 为 1.30 的 液 体 时,根
据单球面折射成像公式得
n1 u
1 公式推导 如图1,设其中折射球面的球心为 C,球面 两 侧
θ(PB 为近轴光线,θ很小),它以入射角i1 射到 球 面 上的B 点,以折射角i2 折射进入另一介质,并与主光 轴交于 P′ 点.此时我们可将 P 和P′ 分别称之为物
櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆
脱太阳的束缚,脱离 太 阳 系 运 动 到 太 阳 系 之 外 的 宇 矛盾.
宙空间.
真 理 的 探 求 是 一 个 过 程 ,要 坚 持 真 理 ,但 要 看 清
量变引 起 质 变,发 射 速 度 的 改 变 引 起 人 造 天 体 真理成立的条件,任 何 客 观 真 理 都 是 绝 对 性 和 相 对
小 角 度 ,式 (11)、(14)、(15)可 写 为
n1θ =n2φ
(16)
θCD =αBC
(17)
φCD =βCE 由 式 (16)、(17)可 得
(18)
( ) α+θ=φ
1+CD BC
n2 n1
=1.07φ >φ
所 考 虑 的 光 线 是 发 散 的 ,故 所 成 的 像 为 虚 像 .由
后所成的像点的位置在 C 点 正 下 方 26.25cm 处 或
在 B 点正下方20.0cm 处.
2.1.2 利用单球折射成像公式解答 (1)当容器内未 装 任 何 液 体 时,根 据 单 球 面 折
1单球面折射公式

f 0.12 1.2
即配戴焦度为7.5D的凸透镜。
32
3、散光眼
散光眼的角膜表面不是球 面,其角膜的各个方向子 午线的半径不相等,点物 发出的光线经角膜折射后 不能形成一清晰的点像, 既散光眼为非对称折射系 统。右图表示散光眼的角 膜及其成像。
散光眼的眼球纵向子午线半径最短,横向子午线的半径最长, 其它方向子午线半径介于二者之间。使得远处的平行光线经 角膜折射后,不能在一点成像。常把一点物看成一条很短的 线条,这就使他看物体时感到模糊不清。
n-n2 1 + 1 = (n -1)( 1 - 1 )
r2 u v
r1 r3 2
二、薄透镜组合
两个或两个以上薄透镜组成的共轴系统, 称为薄透镜组合,简称透镜组。
4
透镜组的成像公式:
二、薄透镜组合
1+1= 1 + 1 u v f1 f2
当υ=∞时,对应的u值即为透镜组的等效焦
距f,则
1= 1+ 1
复习
1、单球面折射公式
n1 + n2 = n2 - n1
2、光焦度 u u
r
f = n2 - n1
r
3、焦距
f1
=
n1 n2 - n1
r
f2
=
n2 n2 - n1
r
1
4、单球面折射成像的高斯公式 :
f1 + f2 = 1
uu
5、 共轴球面系统:逐次成像法
2
6、 薄透镜公式
n1+ n2= n - n1 u v r1
于远视眼的近点较正视眼远些,因此,远视眼在看 眼前较近的物体时,所选择的凸透镜必须将此 物体的虚象成在远视眼的近视点处。
非近轴光线单球面折射成像的精确公式及应用

非近轴光线单球面折射成像的精确公式及应用
毕会英;贺国珠
【期刊名称】《物理通报》
【年(卷),期】1999(000)005
【摘要】近轴光线单球面折射成像公式及由其推导出的透镜成像公式的高斯形式
在几何光学中非常重要。
但它只是近似公式,不能用以解释透镜成像的球差等问题。
本文以光的折射定律为基础,引进参数h、△,建立了非近轴光线单球面折射成像的精确公式,并以眼睛的光学模型为例,讨论了非近轴光线经单球面折射、透镜折射成像
的球差,阐明了晶状体中央折射率较高这一特点有利于消除球差的物理机制,对单片
消球差透镜、人工晶状体的研制具有指导意义。
1 非近轴光线的单球面折射如图1.两媒质折射率为n_1,n_2,分界面曲率半径r,入射光线和主光轴夹角为θ,与分界面交于P点,P点距主光轴距离为h,分析物距u、像距v的关系。
【总页数】2页(P13-14)
【作者】毕会英;贺国珠
【作者单位】新乡医学院物理教研室;新乡医学院物理教研室
【正文语种】中文
【中图分类】O435
【相关文献】
1.推荐一个有用的几何光学公式——单球面折射物像公式 [J], 刘克杰
2.梯度折射率介质的近轴光线追迹 [J], 张思炯;傅瑞斯;等
3.负折射率材料单球面近轴成像奇特规律的研究 [J], 谈苏庆;高文琦
4.单球面折射成像公式及其应用 [J], 张家乐;王化银
5.旋转二次曲面折射成像的精确公式及应用 [J], 郑世旺
因版权原因,仅展示原文概要,查看原文内容请购买。
3-4__球面折射成像
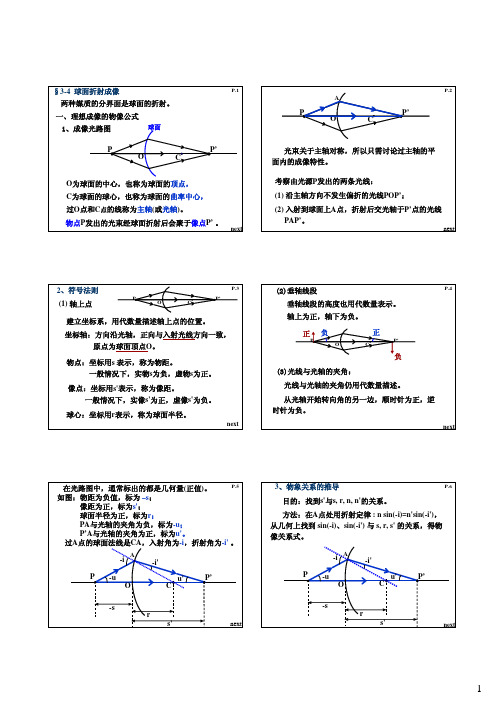
§3-4 球面折射成像 两种媒质的分界面是球面的折射。
一、理想成像的物像公式 1、成像光路图 P球面P.1P.2APOP’ COP’ C光束关于主轴对称,所以只需讨论过主轴的平 面内的成像特性。
考察由光源P发出的两条光线: (1) 沿主轴方向不发生偏折的光线POP’; (2) 入射到球面上A点,折射后交光轴于P’点的光线 PAP’。
next nextO为球面的中心,也称为球面的顶点, C为球面的球心,也称为球面的曲率中心, 过O点和C点的线称为主轴(或光轴)。
物点P发出的光束经球面折射后会聚于像点P’ 。
2、符号法则 (1) 轴上点P O C P’P.3(2)垂轴线段 垂轴线段的高度也用代数量表示。
轴上为正,轴下为负。
正PP.4建立坐标系,用代数量描述轴上点的位置。
坐标轴:方向沿光轴,正向与入射光线方向一致, 原点为球面顶点O。
物点:坐标用s 表示,称为物距。
一般情况下,实物s为负,虚物s为正。
像点:坐标用s'表示,称为像距。
一般情况下,实像s'为正,虚像s'为负。
球心:坐标用r表示,称为球面半径。
next负 ?O C正 ?P’负 (3)光线与光轴的夹角: 光线与光轴的夹角仍用代数量描述。
从光轴开始转向角的另一边,顺时针为正,逆 时针为负。
nextP.5 在光路图中,通常标出的都是几何量(正值)。
如图:物距为负值,标为 –s; 像距为正,标为s'; 球面半径为正,标为r; PA与光轴的夹角为负,标为-u; P’A与光轴的夹角为正,标为u'。
过A点的球面法线是CA,入射角为-i,折射角为-i' 。
3、物象关系的推导 目的:找到s'与s, r, n, n'的关系。
方法:在A点处用折射定律 : n sin(-i)=n'sin(-i'), 从几何上找到 sin(-i)、sin(-i') 与 s, r, s' 的关系,得物 像关系式。
几何光学(医用物理)
u[nn0(11)]1 n0 r1 r2
f1
第一焦点 相应的物点 第一焦距
负 值 球 心 在 物 方
若 u= v第1二[焦n1点n0nn0相(r应1n10的(像r112点)]第11二) 焦f 2距 u v n0 r1 r2
11
11-2 透镜成像
一、单薄透镜成像
n0
11nn0 (11)
n
n 0 u v n0 r1 r2
n1
n2
i1
P
y i2
rC
u
由折射定律:n1sini1n2sini2
i1 i2
对于近轴折射:
sin i1 i1 sini2 i2 n1i1 n2i2
tan y
u
tan y
r
tan y
v
v
i1
y u
y r
i2
y r
y v
n1(u yry)n2(ryvy)
n1 n2 n2 n1 uv r
tan y
f
25cm f
25cm
y
f
36
11-5 医用光学仪器
二、光学显微镜
1、成像原理
放大率:
y
M
25cm
y'
fe
y ''
y
25cm
物 镜 Lo
目 镜 Le
fo
y'
y
M y' 25cm m
y
fe
物镜放大率
目镜放大率
fe
s
m= y' s fe s
y
fo
fo
37
11-5 医用光学仪器
解:(1) f [(n1)(11)]1 r1 r2
单球面物象折射公式及其应用
引言(绪论)光学中以光线概念为基础研究光的传播和成像规律的一个重要分支是几何光学.在几何光学中,折射定律的发现标志着光线传播定律的最终确立,费马原理即是解释、证明和概括光线传播实验定律的途径之一. 本文依据费马原理,推导出了近轴光线条件下的单球面物像折射公式.应用近轴光线条件下的单球面物像折射公式,可以推导出多种情况下的成像公式,为研究复杂的光学系统成像提供了基础性的理论依据,以说明单球面物像折射公式在几何光学中的基础重要性.1 符号法则为了研究光线经由球面反射和折射后的光路,必须先说明一些概念以及规定适当的符号法则,以便使所得的结果能普遍适用,方便读者阅读.图1 主平面内的球面反射图1中的AOB表示球面的一部分.这部分球面的中心点O称为顶点,球面的球心C 称为曲率中心,球面的半径称为曲率半径,连接顶点和曲率中心的直线CO称为主轴,通过主轴的平面称为主平面.主轴对于所有的主平面具有对称性.因此只需讨论一个主平面内光线的反射情况.图1表示球面的一个主平面.在计算任一条光线的线段长度和角度时,对符号作如下规定:(1)线段长度都从顶点算起,凡光线和主轴的交点在顶点右方的,线段长度的数值为正;凡光线和主轴的交点在顶点左方的,线段长度的数值负.物点或像点至主轴的距离,在主轴上方的为正,下方的为负.(2)光线方向的倾斜角度都从主轴(或球面法线)转向有关光线时,若沿顺时针方向移动,则该角度为正;若沿逆时针方向转动,则该角度为负(再考虑角度的符号时,不必考虑组成该角的线段的符号).(3)在图中出现的长度和角度(几何量)只用正值.例如s表示的某线来表示该线段的几何长度.下讨论都假定光线自左向右传段的值是负的,则应用s播.(4)特俗情况下的,文中均在相应位置另有特殊解释说明.2 单球面物象折射公式的推导2.1 球面折射的一般分析设有两种透明均匀的各向同性的介质,界面∑为球面的一部分,两侧介质折射率分别为n 和'n 且n<'n ,如图2所示,折射球面∑的曲率中心C 与顶点O 的连线为主光轴,简称主轴(∑面关于主轴的旋转对称面).图2 光在单球面上的折射设主光轴上面顶点O 的左方有一真实发光点P ,他发出的同心光束的任意一条光线自左向右入射到∑面上的M 点,相应的折射与主轴交与'P 点.以球面顶点O 为计量原点,记球面曲率半径,'',,OC s OP s OP r ===,l PM =''l MP =ϕ=∠MOC . 则PMP’的光程为∆'PMP =''l n nl +在PMC ∆和'MCP ∆中应用余弦定理,并注意()ϕπϕ--=c o s c o s()r s PC +-= r s CP -=''可得 ()()ϕcos 222s r r r s r l --+-=()()ϕcos '2''22r s r r r s l -++-=因此,光线PMP 的光程可写成∆'P M P =ϕϕcos )'(2)'('cos )(2)(2222r s r r s r n s r r s r r n -+-++---+ 式(2-1)根据费马原理,光程变化率应为0,即0d d =ϕl 式(2-2) 代入∆'PMP 的表达式进行求导,有ϕϕϕϕcos )'(2)'(sin )'(2'cos )(2)(sin )(22222r s r r s r r s r n s r r s r r s r r n -+-+--=---+-经计算整理后可得到⎥⎦⎤⎢⎣⎡-+---=---)'('1)(1)cos 1(2)'('')(22222222r s n s r n r r s n s s r n s ϕ 式(2-3) 给定s 和ϕ可由式(2-3)定出.一般来说,'s 与ϕ有关,这意味着由同一P 点发出的同心光束中的各条光线,经∑面折射后,不再汇交与一点,即球面折射破坏了光束的同心性,使轴上发光点不能成像.有两种特殊情况值得注意.其一,令式(2-3)两端同时等于零,即222222)'('')(s r s n s s r n ---=0 式(2-4))'('1)(122r s n s r n -+-=0 式(2-5)求解这组联立方程的解,从而把s 和s’同时确定下来,它们均与ϕ无关,此时的P 和'P 是一对特殊的共轭点,称为球面折射的齐明点或不晕点.对一对齐明点,宽光束经球面折射后仍能成像.其二是把光束限制在近轴区域内,即1cos ≈ϕ,此种的讨论,详见下文.2.2 近轴光线的单球面折射2.2.1 物象距公式在近轴光线的条件下,ϕ值很小,在一级近似下,1cos ≈ϕ,因此式(2-3)中的0)cos 1(≈-ϕ,'s 与ϕ近似无关,则有 222222)'('')(r s n s r s n s -=- 式(2-6)将上面等式两端同时开放,经数学处理后,可得如下简单关系式: rn n s n s n -=-''' 式(2-7) 上式表明,在n 、'n 和r 给定的条件下,在近轴区,轴上物点P 经球面∑折射后可在轴上得一相应的像点'P .从球面顶点O 到像点'P 的距离's 称为像距;从球面顶点O 到P 的距离s 称为物距;'n 和n 分别称为像方折射率和物方折射率,式(2-7)称为球面折射近轴成像的物象距公式.此式对凹球面同样成立.2.2.2 焦距公式如果位于主轴上的物点位置改变,则与之共轭的像点在主轴上的位置必有相应改变.轴上无限远处物点的共轭像点称为折射面的像方焦点,记作'F ;面顶点O 到像方焦点'F 的距离称为像方焦距,记作'f ,轴上无限远处像点的共轭物点称为折射球面的物方焦点,记作F ;球面顶点O 到物方焦点F 的距离称为物方焦距,记作f .由前文关于物距、像距的的符号规则可知:当'F 在O 点右方时'f >0,在O 点左方时'f <0;当F 在O 点左方时f>0,在O 点右方时f<0.根据式(2-7)及上述焦点的定义,可知:当 -∞=s 时nn r n s f -=='''' 式(2-8) 当 ∞='s 时 n n nr s f --==' 式(2-9) 可见,折射球面的两个焦距与它的几何形状(r )及其两侧介质折射率(n ,'n )有关,由式(2-8)和式(2-9)可得两个焦距之比为 nn f f ''-= 式(2-10) 上式表明,折射球面的两个焦距数值一般不等,但符号相反,因此,相应的两个焦点必定分居球面顶点两侧不等距离处.2.2.3 球面折射近轴物点近轴成像如图2所示,主轴上的P 、'P 是一对共轭点.设想将主轴绕折射球面曲率中心C 并在图面内沿顺时针方向旋转一小角度θ,主轴变成副轴,P 、'P 点分别转到Q 、'Q 点.由于球对称性,Q 、'Q 必然也是一对共轭点,这就证明了近轴物点可以成像.由于θ角很小(在近轴区),可以认为弧PQ ≈PQ ,弧''Q P ≈''Q P ,且''P Q QP 和近似地垂直于主轴,P 、'P 点分别是Q 、'Q 点在主轴上的的垂足,所以s 和's 分别为近轴物点Q 的物距和像点'Q 的像距,它们满足式(2-7).近轴物点及其共轭像点到主轴的距离分别为物高和像高,用y 和'y 表示.引入横向放大率β,其定义为像高和物高之比,即 yy '≡β 式(2-11)在近轴区的条件下,i i =sin ,又由折射定律,可得''i n ni = 式(2-12)图3 单球面折射近轴物点成像即有 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-'''s y n s y n 式(2-13) 由式(2-11),可以得到横向放大率公式 sn ns ''=β 式(2-14) 3.单球面物像折射公式的应用3.1 高斯公式的推导把式(2-8)和式(2-9)代入式(2-7)可得,''''f n f n s n s n =-=- 或 1''=+sf s f 式(3-1) 此式便是普遍的物像公式,称为高斯物像公式.3.2 牛顿公式的推导如图4,在确定物点P 和像点'P 的位置后,我们把物距和像距分别从物方焦距和像方焦距算起.物点在F 之左的,物距FP 用x -表示;像点在'F 之右的,像距P F '用'x +表示.反之亦然.这样就有()()f x s -+-=- ()()'''x f s +++=图4 顶点为物方和像方焦点时的物距和像距示意图代入式(3-1)可得1'''=+++fx f f x f 即有''ff xx = 式(3-2) 此式便是牛顿公式.3.3 近轴光线单球面反射公式的推导对于反射情况,这里利用焦距和折射率的关系,从两方面入手进行讨论与推导.下面先就焦距与折射率的关系开始进行讨论.关于焦距和折射率的关系,已在上文中给出了具体的关系式,即式(2-10). 在球面反射的情况中,物空间与像空间重合,且反射光线与入射光线的传播方向恰恰相反.这一情况,在数学处理上可以认为像方介质的折射率'n 等于物方介质折射率n 的负值,即nn -='(这仅在数学上有意义)。
几何光学
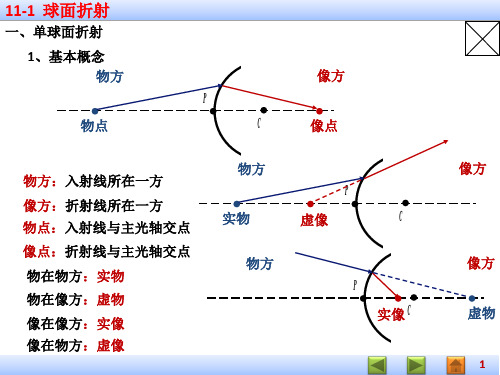
第十一章 几何光学§11-1 球面成像一、单球面折射当两种不同折射率的透明媒质的分界面为球面的一部分时,所产生的折射现象称为单球面折射。
应用此公式时应注意:1、符号规则实物、实像到折射顶点的距离p 、p ’ 取正;虚物、虚像到折射顶点的距离p 、p ’取负;凸球面对着光线r 取正;反之取负。
2、n 1为入射光线所在空间的折射率,称物方折射率; n 2为出射光线所在空间的折射率,称像方折射率。
3、近轴光线,否则不能会聚同一点。
二、焦度Φ、焦点F 、焦距fΦ=-=11211n r n n n fΦ=-=21222n r n n n f3、高斯成像公式给定折射球面(f 1、f 2、),成像公式可变为如下形式r n n p n p n 12'21-=+D rn n 单位为屈光度焦度,12-=Φ11'21'2112'21=+=+=-=+pf p f p n p n r n n p n p n φφφ4、平面折射、视深对平面折射(r=∝),像距p ’,称视深。
p n n p 12'-=二、共轴球面系统 coaxial spherical system两个或两个以上的折射球面的曲率中心在同一直线上的折射系统,称共轴球面系统,简称共轴系统。
采用依次成像法 等效光路法§11-2 透镜透镜:两个折射球面的共轴系统类型:形状分凸透镜、凹透镜功能分会聚透镜、发散透镜薄透镜:厚度d<<物距p,像距p’、半径r 的情形一、 薄透镜公式薄透镜的焦度公式凸透镜f>0 凹透镜f<0应用此公式时应注意同上二、薄透镜组合 f p p r r n n n f r r n n n p p 111)]11)([(1)11)((11'21002100'=+--=--=+得高斯成像公式)],11)([(2100r r n n n --=Φ焦度两个或两个以上的薄透镜组成的共轴系统。
符号法则单个折射球面成像
几何光学基础
1
§1.3 光路计算
所谓成像过程,就是物光束经光学系统逐次折、反射 的结果。
光在各向同性、均匀介质中总是沿直线传播的改变方 向只有在界面上进行,所以,把单个折射球面的问题搞清 楚了,那么由多个球面组成的系统的问题亦就迎刃而解。
2
一、 基本概念与符号规则
设在空间存在如下一个折射球面:
讨论:
① 当 n n' 时 1 无折射面 ② 0 正像, 物像同方向, y, y' 同号
③ 0 倒像,物像逆方向, y, y' 异号
④ 0 l,l' 同号物像虚实相反(物像同侧) ⑤ 0 l,l' 异号物像虚实相同(物像异侧)
⑥ 1 放大, 1 缩小
⑦ 0 l 即无穷远物将在某点缩
在近轴区域内,通过物点的光线经过光学系统后,必然通过 相应的像点,这样一对共轭光线与光轴夹角u 和u′的比值,称 为角放大率,以希腊字母γ表示
u
u
利用关系式 lu lu ,上式可写为
l
l
可得 n ·1
n
4.三放大率之间的关系
n 2·n ·1
n n
27
5.拉亥不变量J
由公式 y / y nl / nl
n
由此式可见,如果物体是一个沿轴放置的正方形,因垂轴放 大率和轴向放大率不一致,则其像不再是正方形。还可以看出, 折射球面的轴向放大率恒为正值,这表示物点沿轴移动,其 25 像点以同样方向沿轴移动。
补充一点:
一个沿轴向有一定厚度的物经成像后,其轴向 高度将不再与物相似。
如图所示
26
3.角放大率γ
反射定律可由折射定律在 n n 时导出。因此, 在折射面的公式中,只要使 n n, 便可直接得到
几何光学知识点总结2
几何光学1.单球面成像公式说明:①适用范围:近轴光线②n 1λ射光线所在媒质折射率,n 2折射光线所 在媒质折射率③符号规则:实物(像)取正,虚物(像)取负;入射光线对着凸面r 取正2、单球面折射系统的焦度、焦点、焦距(1)焦度((focal power ) φ——反映系统折光本领r n n p n p n 1221-='+rn n 12-=φ单位:屈光度D (r 单位为 m )(2)焦距:(3)焦距和焦度的关系3.共轴球面系统采用顺次成像法4.薄透镜:分类凸透镜、凹透镜度1001=D r n n n f 1211-=r n n n f 1222-=r n n 12-=φr n n n f 1211-=r n n n f 1222-=11f n =φ22f n =如果组成透镜的材料折射率大于镜外介质的折射率,凸透镜是会聚透镜;否则是发散透镜。
成像公式:)11)(('21000r r n n p n p n --=+)11('112100r r n n n p p --=+f n 0=φ在空气中f1=φ6.薄透镜A.薄透镜的成像与单个透镜成像没有区别,可以用对每一个透镜依次成像的方法解决。
B.空气中密接的薄透镜组21ΦΦΦ+=21111f f f +=7、眼的调节瞳孔改变:球面像差,光通量晶状体r变:焦度改变r调节有一定限度:近点:眼睛处于最大调节状态能看清的物体与眼睛之间的距离。
正常眼:10-12cm远点:眼睛不调节时,能看清的最远处物体与眼睛之间的距离,正常眼:∞近视眼远点变近明视距离:适当照明,不易疲劳,最适宜距离 25 cm8.视角:从物体上两点发出的光到眼节点(光心)所张的角。
影响因素:物体大小物体与眼睛之间的距离意义:视角决定了视网膜上像的大小。
9.视力—眼的分辨本领:国家标准对数视力表国际标准视力表10.眼的屈光不正及矫正θ'-=lg 5L θ'=1视力11.放大镜放大镜的角放大率:12.显微镜:a.放大率b.显微镜的最小分辨距离; 如何提高显微镜的分辨本领?(1)减小照射光波的波长紫外光代替可见光,分辨本领提高一倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(9)
BE = BA -AC +CE = (8.0-1.75+9.75)cm =16.0cm (10) B 点发 出 的 光 线 通 过 平 凸 玻 璃 柱,在 玻 璃 柱 对
称轴上所成的像点的位置在C 点正上方9.75cm 处
或在 B 点正上方16.0cm 处.
(2)容 器 底 部 凸 面 两 侧 介 质 的 折 射 率 分 别 是
v =8.0cm 所 成的像点的位置在A 点正上方8.0cm 处,即
B 点正上方16.0cm 处.
— 53 —
2016年第3期 物理通报 竞赛与物理专题研修
(2)当容器内装满折射 率 为 1.30 的 液 体 时,根
据单球面折射成像公式得
n1 u
最终轨道位置的改变.任 何 事 物 量 变 的 积 累 都 会 引 起 质 变 ,量 变 的 积 累 会 引 起 质 变 的 飞 跃 .
性的统一.任何真理 性 的 认 识 都 是 从 相 对 真 理 向 绝 对真理转化过程中的一个环节.
7 真理是相对的
8 结语
真理都 是 有 条 件 的.任 何 真 理 都 有 自 己 适 用 的 条 件 和 范 围 ,如 果 超 出 了 这 个 条 件 和 范 围 ,只 要 再 多 走 一 小 步 ,真 理 就 会 变 成 谬 误 .物 理 理 论 也 不 是 绝 对 的 真 理 ,有 其 适 用 的 条 件 和 范 围 .
度 ,式 (1)、(4)、(5)可 写 为
n1θ =n0φ
(6)
2016年第3期 物理通报 竞赛与物理专题研修
θCD =αBC φCD =βCE 由 式 (6)、(7)可 得
(7) (8)
( ) α+θ=φ
1+CD BC
图2
2.1.1 原解答 (1)容 器 底 部 凸 面 两 侧 介 质 的 折 射 率 分 别 是
n1 =1.56和n0 =1.0.如图3,由 B 点发出的经过球 心C 的光线BA 经过顶点A 后,方向不变,进入空气 中;由B 点发出的与BA 成α 角的另一条光线BD 在 D 点折射,设折射角为φ,并与前一条出射光线交于 E 点,E 点即B 点的像点的位置.
小 角 度 ,式 (11)、(14)、(15)可 写 为
n1θ =n2φ
(16)
θCD =αBC
(17)
φCD =βCE 由 式 (16)、(17)可 得
(18)
( ) α+θ=φ
1+CD BC
n2 n1
=1.07φ >φ
所 考 虑 的 光 线 是 发 散 的 ,故 所 成 的 像 为 虚 像 .由
式(12)、(13)、(16)、(17)、(18)得
CE = φCD =
1
CD
β
n2 n1
+BCDCnn21
-1
将有关数据代入上式可得
CE = 11..3506+8.01-.7151.75×11..3506-1×
1.75cm =26.25cm
(19)
由 式 (19)和 题 给 数 据 得
BE = AC +CE -AB = (1.75+26.25-8.0)cm =20.0cm (20) B 点发 出 的 光 线 通 过 平 凸 玻 璃 柱,第 一 次 折 射
图3
由折射定律和几何关系得
n1sinθ =n0sinφ γ =α+θ
(1) (2)
φ =γ+β
(3)
在三角形 BCD 和三角形CDE 中 ,由正弦定理可得
CD sinα
=
BC sinθ
(4)
CD sinβ
=
CE sinφ
(5)
由于只 考 虑 近 轴 光 线 成 像,所 以α,β,θ,φ 都 是 小 角
=
n2 n1
λ 1时,sinλ ≈λ. (1)当容器内未装 任 何 液 体 时,求 从 B 点 发 出
的光线通过平凸玻璃 柱,在 玻 璃 柱 对 称 轴 上 所 成 的 像 的 位 置 ,并 判 断 像 的 虚 实 ;
(2)当容器内装满折射 率 为 1.30 的 液 体 时,求 从B 点发出的光线通过平凸玻璃柱的上表面折射后 所 成 像 点 的 位 置 ,并 判 断 这 个 像 的 虚 实 .
如 图 5 所 示 ,一 细 长 的 圆 柱 形 均 匀 玻 璃 棒 ,其 一 个 端 面 是 平 面 (垂 直 于 轴 线 ),另 一 个 端 面 是 球 面 ,球
心位于轴线上.现有 一 根 很 细 的 光 束 沿 平 行 于 轴 线 方 向 且 很 靠 近 轴 线 入 射 .当 光 从 平 端 面 射 入 棒 内 时 ,
学生不易理解.若直 接 利 用 球 面 介 质 对 光 线 折 射 的 轴.设P 为主光轴上一物点,从P 发出的光线PA 正
普通规律 ——— 单球面折射成像公式,则能使得求解 入射到球面上,它将无偏折地进入另一介质,并通过
过程快速而简洁.
球心 C.从 P 点发出 的 另 一 光 线 PB 与 主 光 轴 成 角
1 公式推导 如图1,设其中折射球面的球心为 C,球面 两 侧
θ(PB 为近轴光线,θ很小),它以入射角i1 射到 球 面 上的B 点,以折射角i2 折射进入另一介质,并与主光 轴交于 P′ 点.此时我们可将 P 和P′ 分别称之为物
櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆
n1 =1.56和n2 =1.30.如图4,由B 点发出的经过 球心C 的光线BA 经过顶点A 后,方向不变,进入液
体 中;由B 点发出的与BA 成α 角的另一条光线BD 在 D 点折射,设折射角为φ,并与前一条出射光线交 E 点,E 点即B 点发出 的 光 线 第 一 次 折 射 后 所 成 像
点的位置.
物 理 教 材 中 蕴 含 着 丰 富 的 哲 学 思 想 ,可 以 说 ,物
理 是 学 习 哲 学 的 资 源 ,哲 学 是 学 习 物 理 的 工 具 .用 哲
学 学 物 理 ,引 导 学 生 形 成 辩 证 唯 物 主 义 的 世 界 观 、方
法 论 .物 理 与 哲 学 教 学 的 渗 透 整 合 ,有 助 于 激 发 学 生
脱太阳的束缚,脱离 太 阳 系 运 动 到 太 阳 系 之 外 的 宇 矛盾.
宙空间.
真 理 的 探 求 是 一 个 过 程 ,要 坚 持 真 理 ,但 要 看 清
量变引 起 质 变,发 射 速 度 的 改 变 引 起 人 造 天 体 真理成立的条件,任 何 客 观 真 理 都 是 绝 对 性 和 相 对
α
=
h R
θ =
h u
β
=
h v
代入上式并整理可得
n1 u
+nv2
=
n2
-n1 R
上式即 为 单 球 面 折 射 时 的 物 像 距 公 式,式 中 各
物理量的正、负取值有 一 定 的 规 则,这 一 规 则 是:入
射光线从左方射来时,球心在界面的右侧,则R 取正 值,球心在界面左侧,则 R 取 负 值;实 物 和 实 像 的 物 距和像距都取正值;虚 物 和 虚 像 的 物 距 和 像 距 都 取
图4
由折射定律和几何关系可得 n1sinθ =n2sinφ γ =α+θ γ =φ+β
(11) (12) (13)
在三角形 BCD 和三角形CDE 中 ,由正弦定理
可得
CD sinα
=
BC sinθ
(14)
CD sinβ
=
CE sinφ
(15)
由于只考虑 近 轴 光 线 成 像,所 以α,β,θ,φ 都 是
2016年第3期 物理通报 竞赛与物理专题研修
单球面折射成像公式及其应用
张家乐 王化银
(淮北市第一中学 安徽 淮北 235000) (收 稿 日 期 :2015-10-17)
摘 要:物理竞赛几何光学球面折射问题的求解,直接利用 单 球 面 折 射 成 像 公 式 ,往 往 能 使 得 求 解 过 程 快 速 而 简洁.
图1
由于i1 和i2 都很 小,故 由 近 似 关 系 应 有 sin i1 =i1,sin i2 =i2,则上式变为
n1i1 =n2i2 又 由图中的几何关系可以看到i1 =α+θ和i2 =α- β,代 入 上 式 便 为
n1 (α+θ)=n2 (α-β) 以h 表示图中B 点到 主 光 轴 的 距 离,R 表 示 球 面 半 径 ,则 由 小 角 的 近 似 关 系 可 以 得 到
+nv2
=
n2
-n1 R
即
解得
18.5.06+1v.30
=
1.30-1.56 -1.75
v =-28.0cm 所成的像点的位置在 A 点 正 下 方 28.0cm 处,
即 B 点正下方20.0cm 处.
2.2 题目2 【例 2】(第 25 届 全 国 中 学 生 物 理 竞 赛 预 赛 第 19
题)
负值.
2 竞赛试题解答
2.1 题目1 【例 1】(第 32 届 全 国 中 学 生 物 理 竞 赛 预 赛 第 16
题 )如图2所示,一垂直放置的高为15.0cm 的圆柱 形中空玻璃容器,其底部玻璃较厚,底部顶点A 点到 容器底平面中心 B 点的距离为8.0cm,底部上沿为 一凸起的球冠,球心C点在A 点正下方,球的半径为 1.75cm.已知空 气 和 容 器 玻 璃 的 折 射 率 分 别 是 n0 =1.0和n1 =1.56.只考虑近轴光线成像.已知:当 — 52 —
关键词:几何光学 球面折射 物理竞赛
单球面折射问题在竞赛试 题 中 时 常 出 现,参 考 解 法 中 用 到 的 式 子 较 多 ,且 进 行 了 较 多 的 近 似 处 理 ,
介质的折射率分别为n1 和n2,且n1 <n2.我们把通 过球面顶 点 和 球 心 的 直 线 称 为 此 折 射 球 面 的 主 光
