直线与圆题型及做题技巧
圆的方程、直线与圆的位置关系题型归纳学生版

圆的方程、直线与圆的关系题型归纳一、学法指导与考点梳理1.圆的方程 (1)圆的方程①标准方程:(x -a )2+(y -b )2=r 2,圆心坐标为(a ,b ),半径为r . ②一般方程:x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0),圆心坐标为⎝⎛⎭⎫-D 2,-E 2,半径r =D 2+E 2-4F 2.(2)点与圆的位置关系①几何法:利用点到圆心的距离d 与半径r 的关系判断:d >r ⇔点在圆外,d =r ⇔点在圆上;d <r ⇔点在圆内.②代数法:将点的坐标代入圆的标准(或一般)方程的左边,将所得值与r 2(或0)作比较,大于r 2(或0)时,点在圆外;等于r 2(或0)时,点在圆上;小于r 2(或0)时,点在圆内. 2.直线与圆的位置关系直线l :Ax +By +C =0(A 2+B 2≠0)与圆:(x -a )2+(y -b )2=r 2(r >0)的位置关系如下表.3.圆与圆的位置关系二、重难点题型突破重难点1 圆的方程求圆的标准方程的常用方法包括几何法和待定系数法.(1)由圆的几何性质易得圆心坐标和半径长时,用几何法可以简化运算.对于几何法,常用到圆的以下几何性质:①圆中任意弦的垂直平分线必过圆心;②圆内的任意两条弦的垂直平分线的交点一定是圆心. (2)由于圆的标准方程中含有三个参数a ,b ,r ,运用待定系数法时,必须具备三个独立的条件才能确定圆的方程.这三个参数反映了圆的几何性质,其中圆心(a ,b )是圆的定位条件,半径r 是圆的定形条件.例1.(1)当a 为任意实数时,直线(a -1)x -y +a +1=0恒过定点C ,则以C 为圆心,5为半径的圆的方程为( )A .x 2+y 2-2x +4y =0B .x 2+y 2+2x +4y =0C .x 2+y 2+2x -4y =0D .x 2+y 2-2x -4y =0(2)已知圆C 关于x 轴对称,经过点(0,1),且被y 轴分成两段弧,弧长之比为2∶1,则圆的方程为( ) A .x 2+⎝⎛⎭⎫y ±332=43B .x 2+⎝⎛⎭⎫y ±332=13C.⎝⎛⎭⎫x ±332+y 2=43D.⎝⎛⎭⎫x ±332+y 2=13【变式训练1】.圆心在曲线y =2x (x >0)上,与直线2x +y +1=0相切,且面积最小的圆的方程为( )A .(x -2)2+(y -1)2=25B .(x -2)2+(y -1)2=5C .(x -1)2+(y -2)2=25D .(x -1)2+(y -2)2=5【变式训练2】.在平面直角坐标系xOy 中,圆C :x 2+y 2+4x -2y +m =0与直线x -3y +3-2=0相切. (1)求圆C 的方程;(2)若圆C 上有两点M ,N 关于直线x +2y =0对称,且|MN |=23,求直线MN 的方程.重难点2 直线与圆的位置关系 判定直线与圆位置关系的常用方法:(1)几何法:根据圆心到直线的距离d 与圆半径r 的大小关系判断. (2)代数法:根据直线与圆的方程组成的方程组的解的个数判断.(3)直线系法:若动直线过定点P ,则点P 在圆内时,直线与圆相交;当P 在圆上时,直线与圆相切或相交;当P 在圆外时,直线与圆位置关系不确定.例2.(1)直线l :y =kx +1与圆O :x 2+y 2=1相交于A ,B 两点,则“k =1”是“|AB |=2”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(2)若圆(x -3)2+(y +5)2=r 2上有且只有两个点到直线4x -3y -2=0的距离等于1,则半径r 的取值范围是( )A .(4,6)B .[4,6]C .(4,5)D .(4,5]【变式训练1】.若直线x -y +m =0被圆(x -1)2+y 2=5截得的弦长为23,则m 的值为( ) A .1 B .-3 C .1或-3D .2【变式训练2】.已知圆C 的方程是x 2+y 2-8x -2y +8=0,直线y =a (x -3)被圆C 截得的弦最短时,直线方程为________.【变式训练3】.在平面直角坐标系中,已知圆在轴上截得线段长为,在轴上截得线段长为(I )求圆心的轨迹方程;(II )若点到直线,求圆的方程. 重难点3 直线、圆方程的综合应用(1)判断或处理直线和圆的位置的问题,一般有两种方法,一是几何法,利用圆的几何性质解题,二是代xOy P x y P P y x P数法,联立圆与直线的方程,利用判别式,根与系数关系来处理,在做题时要用心作图,很多题目要用到数形结合的思想.(2)若,()P x y 是定圆222()()C x a y b r -+-=:上的一动点,则mx ny +和yx这两种形式的最值,一般都有两种求法,分别是几何法和代数法.①几何法.mx ny +的最值:设mx ny t +=,圆心(,)C a b 到直线mx ny t +=的距离为22d m n=+,由d r =即可解得两个t 值,一个为最大值,一个为最小值.y x 的最值:yx即点P 与原点连线的斜率,数形结合可求得斜率的最大值和最小值. ②代数法.mx ny +的最值:设mx ny t +=,与圆的方程联立,化为一元二次方程,由判别式等于0,求得t 的两个值,一个为最大值,一个为最小值.y x 的最值:设yt x=,则y tx =,与圆的方程联立,化为一元二次方程,由判别式等于0,求得t 的两个值,一个为最大值,一个为最小值.例3.(1)已知点P 的坐标(x ,y )满足⎩⎪⎨⎪⎧x +y ≤4,y ≥x ,x ≥1,过点P 的直线l 与圆C :x 2+y 2=14相交于A ,B 两点,则|AB |的最小值是( )A .2 6B .4 C. 6 D .2(2)著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:(x -a )2+(y -b )2可以转化为平面上点M (x ,y )与点N (a ,b )的距离.结合上述观点,可得f (x )=x 2+4x +20+x 2+2x +10的最小值为________.【变式训练1】.已知圆C :x 2+y 2-4x -6y +12=0,点A (3,5). (1)求过点A 的圆的切线方程;(2)O 点是坐标原点,连接OA ,OC ,求△AOC 的面积S .【变式训练2】.在平面直角坐标系xoy 中,曲线261y x x =-+与坐标轴的交点都在圆C 上.(I )求圆C 的方程;(II )若圆C 与直线0x y a -+=交于A ,B 两点,且,OA OB ⊥求a 的值.三、课堂定时训练(45分钟)1.(2020黑龙江黑河一中高二期中)已知A (3,-2),B (-5,4),则以AB 为直径的圆的方程是( ) A .(x -1)2+(y +1)2=25 B .(x +1)2+(y -1)2=25 C .(x -1)2+(y +1)2=100 D .(x +1)2+(y -1)2=1002.(2020山东潍坊三中高二期中)已知以点A (2,-3)为圆心,半径长等于5的圆O ,则点M (5,-7)与圆O 的位置关系是( )A .在圆内B .在圆上C .在圆外D .无法判断3.(2020福建莆田一中高二月考)过点()()1,1,1,1A B --,且圆心在直线20x y +-=上的圆的方程是( ) A .()()22314x y -++= B .()()22314x y ++-= C .()()22114x y -+-=D .()()22114x y +++=4.(2020邢台市第八中学高二期末)方程220x y Dx Ey F ++++=表示以(2,3)-为圆心,4为半径的圆,则D,E,F 的值分别为( ) A .4,6,3-B .4,6,3-C .4,6,3--D .4,6,3--5.(2020·全国高二课时练习)直线y=x+1与圆x 2+y 2=1的位置关系为( ) A .相切 B .相交但直线不过圆心 C .直线过圆心 D .相离6.(2020山东泰安实验中学高二期中)0y m -+=与圆22220x y x +--=相切,则实数m 等于( )A 或B .C .-D .-7.(2020全国高二课时练)与圆()22:136C x y -+=同圆心,且面积等于圆C 面积的一半的圆的方程为_________.8.(2020·上海高二课时练习)若圆22(1)(4)5x y -+-=的圆心到直线0x y a -+=的距离为2,则a 的值为_________.9.(2020湖南师大附中高二期中)已知点()()1,2,1,4A B --,求(1)过点A,B 且周长最小的圆的方程; (2)过点A,B 且圆心在直线240x y --=上的圆的方程.10.已知直线l :4x +3y +10=0,半径为2的圆C 与l 相切,圆心C 在x 轴上且在直线l 的右上方. (1)求圆C 的方程;(2)过点M (1,0)的直线与圆C 交于A ,B 两点(A 在x 轴上方),问在x 轴正半轴上是否存在定点N ,使得x 轴平分∠ANB ?若存在,请求出点N 的坐标;若不存在,请说明理由.。
直线与圆的高考常见题型总结

Copyright©博看网. All Rights Reserved.
知识篇 新高考名师护航
高二数学 2023 年 10 月
解得
5
a)≤ (
a-3)+2 ,
2
2
2
1
3
≤a≤ 。
3
2
(
2
0
2
3 年 新 高 考 Ⅰ 卷 )过 点 (
0,
例 6
与圆 x2 +y2 -4
-2)
x-1=0 相 切 的 两 条 直
y -2)<1,
2
2
,
方程 xc
o
sθ+ (
s
i
nθ=1(
0≤θ≤2π)
θ
y-2)
无解。因此经过任意点的直线均为有限个。
Copyright©博看网. All Righ识篇 新高考名师护航
高二数学 2023 年 10 月
(
对于 B:
不在任一直线上。
0,
2)
对于 C:
做圆 x + (
y-2)=1 的 外 切 正
2
故选 ABD。
2
n 边形 即 可。 (将 正 n 边 形 的 中 心 置 于 (
0,
,
中心到边的距离 设 为 1,此 正 n 边 形 即 满
2)
足题意)
例 4
2
x-y-3=0 的距离为(
5
A.
5
对 于 D:注 意 到 任 意 三 条 直 线 若 能 围 成
高考热点 2
2
(写 出 所 有 真
其中真命 题 的 代 号 是
。
命题的代号)
高中数学直线与圆解题技巧

高中数学直线与圆解题技巧在高中数学中,直线与圆是常见的几何图形,解题时需要掌握一些技巧。
本文将围绕直线与圆的解题技巧展开讨论,并通过具体题目举例,帮助读者更好地理解和应用这些技巧。
1. 直线与圆的位置关系直线与圆的位置关系有三种情况:直线与圆相切、直线与圆相交和直线与圆相离。
解题时,首先要确定直线与圆的位置关系,然后根据不同情况选择合适的方法解题。
例如,已知直线L的方程为y = 2x + 1,圆C的方程为(x - 2)^2 + (y - 3)^2 = 4,求直线L与圆C的位置关系。
解题思路:首先,我们可以将直线L的方程代入圆C的方程,得到一个关于x的二次方程。
如果二次方程有两个不相等的实根,则直线与圆相交;如果二次方程有两个相等的实根,则直线与圆相切;如果二次方程无实根,则直线与圆相离。
将直线L的方程代入圆C的方程:(x - 2)^2 + (2x + 1 - 3)^2 = 4化简得:5x^2 - 8x - 12 = 0解二次方程5x^2 - 8x - 12 = 0,得到两个实根x1 = -1,x2 = 2.4。
由于二次方程有两个不相等的实根,所以直线L与圆C相交。
2. 直线与圆的切线直线与圆相切时,我们需要求直线的斜率和切点坐标。
通过求解切线方程,可以得到直线与圆的切点和切线斜率,从而解题。
例如,已知圆C的方程为(x - 3)^2 + (y - 4)^2 = 9,求过点P(2, 1)的直线与圆C 的切点和切线方程。
解题思路:首先,我们可以计算点P到圆C的距离,如果点P到圆C的距离等于圆C的半径,则点P在圆C上,直线与圆C相切。
计算点P到圆C的距离:d = √[(2 - 3)^2 + (1 - 4)^2] = √10由于点P到圆C的距离等于圆C的半径3,所以点P在圆C上,直线与圆C 相切。
接下来,我们需要求直线的斜率和切点坐标。
直线的斜率可以通过点P和圆心的连线来求解。
直线的斜率:k = (1 - 4) / (2 - 3) = 3切点坐标可以通过直线的斜率和圆的方程来求解。
(完整版)直线与圆知识点及经典例题(含答案)

(完整版)直线与圆知识点及经典例题(含答案)圆的方程、直线和圆的位置关系【知识要点】一、圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆(一)圆的标准方程222()()x a y b r -+-= 这个方程叫做圆的标准方程。
王新敞说明:1、若圆心在坐标原点上,这时0a b ==,则圆的方程就是222x y r +=。
2、圆的标准方程的两个基本要素:圆心坐标和半径;圆心和半径分别确定了圆的位置和大小,从而确定了圆,所以,只要,,a b r 三个量确定了且r >0,圆的方程就给定了。
就是说要确定圆的方程,必须具备三个独立的条件王新敞确定,,a b r ,可以根据条件,利用待定系数法来解决。
(二)圆的一般方程将圆的标准方程222)()(r b y a x =-+-,展开可得02222222=-++--+r b a by ax y x 。
可见,任何一个圆的方程都可以写成 :220x y Dx Ey F ++++= 问题:形如220x y Dx Ey F ++++=的方程的曲线是不是圆?将方程022=++++F Ey Dx y x 左边配方得:22224()()22D E D E Fx x +-+++=(1)当F E D 422-+>0时,方程(1)与标准方程比较,方程022=++++F Ey Dx y x 表示以(,)22D E--为圆 224D E F+-,(3)当F E D 422-+<0时,方程022=++++F Ey Dx y x 没有实数解,因而它不表示任何图形。
圆的一般方程的定义:当224D E F +->0时,方程220x y Dx Ey F ++++=称为圆的一般方程. 圆的一般方程的特点:(1)2x 和2y 的系数相同,不等于零;(2)没有xy 这样的二次项。
(三)直线与圆的位置关系 1、直线与圆位置关系的种类(1)相离---求距离;(2)相切---求切线;(3)相交---求焦点弦长。
直线与圆的位置关系题型归纳

直线与圆的位置关系题型归纳引言在几何学中,直线和圆是基本的几何元素。
研究直线与圆的位置关系不仅有助于理解几何学基本原理,还可以应用到实际问题中。
本文将归纳总结几种常见的直线与圆的位置关系题型,并给出相应的解题方法。
一、直线与圆相交直线与圆相交通常有三种情况:直线与圆相切、直线穿过圆、直线既与圆相切又穿过圆。
1. 直线与圆相切当直线与圆只有一个交点时,称直线与圆相切。
这种情况下,直线与圆的位置关系相对简单。
求解这类问题时,可以利用以下方法: - 根据已知条件确定直线方程和圆的方程。
- 将直线方程和圆的方程联立,求解交点的坐标。
- 判断交点是否满足直线方程和圆的方程,从而确定直线与圆相切。
2. 直线穿过圆当直线与圆有两个交点时,称直线穿过圆。
这种情况下,需要进一步确定直线与圆的具体位置关系。
求解这类问题时,可以按照以下步骤进行: - 利用已知条件确定直线方程和圆的方程。
- 将直线方程和圆的方程联立,求解交点的坐标。
- 判断交点的坐标与圆心的位置关系,从而确定直线与圆的位置关系。
3. 直线既与圆相切又穿过圆当直线与圆既有一个交点又有两个交点时,称直线既与圆相切又穿过圆。
这种情况下,需要进一步确定直线与圆的具体位置关系。
求解这类问题时,可以按照以下步骤进行: - 利用已知条件确定直线方程和圆的方程。
- 将直线方程和圆的方程联立,求解交点的坐标。
- 判断交点的坐标与圆心的位置关系,从而确定直线与圆的位置关系。
二、直线与圆相离直线与圆相离是指直线与圆没有交点。
这种情况下,直线与圆的位置关系相对简单。
求解这类问题时,可以按照以下步骤进行: - 利用已知条件确定直线方程和圆的方程。
- 求解直线方程和圆的方程的解集。
- 判断解集是否为空集,从而确定直线与圆相离。
三、总结与应用对于直线与圆的位置关系题型,我们可以通过确定直线方程和圆的方程,求解交点的坐标,判断交点的坐标与圆心的位置关系来确定直线与圆的位置关系。
解答直线与圆的位置关系问题的三种方法

直线与圆的位置关系主要有三种:相切、相交、相离.判断直线与圆的位置关系问题的常见命题形式有:(1)根据直线与圆的方程判断二者的位置关系;(2)根据直线与圆的位置关系求参数的值或取值范围.解题的关键在于明确直线与圆的位置关系,建立代数或几何关系.下面主要谈一谈解答直线与圆的位置关系问题的三种方法.一、几何法运用几何法求解直线与圆的位置关系问题,需先根据圆的方程确定圆心、半径;然后根据点到直线的距离公式求得圆心到直线的距离,或根据圆的半径、弦心距、弦长之间的关系,利用勾股定理求得圆心到直线的距离;再判断圆心到直线距离d 与半径r 的大小关系.一般地,①当r >d 时,直线与圆相交;②当r =d 时,直线与圆相切;③当r <d 时,直线与圆相离.例1.直线l :y =kx +1(k <0)与圆C :x 2+4x +y 2-2y+3=0相切,则直线l 与圆D :(x -2)2+y 2=3的位置关系是().A.相交B.相切C.相离D.不确定解:因为圆C 的标准方程为(x +2)2+(y -1)2=2,所以圆的圆心为(-2,1),半径为2,因为直线l 与圆C 相切.所以||-2k -1+1k 2+1=2,解得k =±1,因为k <0,所以k =-1,所以直线l 的方程为x +y -1=0.圆心D (2,0)到直线l 的距离:d =2+0-1=3,所以直线l 与圆D 相交.故选A 项.由于直线l :y =kx +1(k <0)与圆C :x 2+4x +y 2-2y +3=0相切,所以可以直接根据圆心到直线的距离等于半径,来建立关系,求得k 的值,即可求得直线l 的方程.根据点到直线的距离公式,求得圆D :(x -2)2+y 2=3的圆心到直线l 的距离,比较该距离与圆D 的半径之间的大小,即可判断出直线l 与圆D 的位置关系.例2.若直线l :x -y +m =0与圆C :x 2+y 2-4x -2y +1=0恒有公共点,则m 的取值范围是().A.[-2,2]B.[-22,22]C.[-2-1,2-1]D.[-22-1,22-1]解:因为圆C 的标准方程为(x -2)2+(y -1)2=4,所以圆的圆心为(2,1),半径为2,由点到直线的距离公式可得圆心到直线的距离d =||2-1+m 2,若直线与圆恒有公共点,则直线与圆相交或相切,所以||2-1+m 2≤2,解得-22-1≤m ≤22-1,故选D 项.要使直线与圆恒有公共点,需使直线与圆相交或相切,那么圆心到直线的距离需小于或等于半径,即d ≤r .根据点到直线的距离公式建立不等关系式,即可求得参数m 的取值范围.例3.已知圆M :()x +cos θ2+()y -sin θ2=1,直线l :y =kx .下面四个命题:(1)对任意实数k 与θ,直线l 和圆M 相切;(2)对任意实数k 与θ,直线l 和圆M 有公共点;(3)对任意实数θ,必存在实数k ,使得直线l 和圆M 相切;(4)对任意实数k ,必存在实数θ,使得直线l 和圆M 相切.其中说法正确的有_______.解:因为圆M :()x +cos θ2+()y -sin θ2=1,所以圆的圆心M ()-cos θ,sin θ,半径为1,所以M 到直线l 的距离d M -l =||-k cos θ-sin θk 2+1,则d2M -l-1=()k cos θ+sin θ2-k 2-1k 2+1=k 2cos 2θ+2sin θcos θ⋅k +sin 2θ-k 2-1k 2+1刘艳林43。
关于圆的题型归纳和解题技巧

关于圆的题型归纳和解题技巧
一、圆的题型归纳
1. 直线与圆的位置关系:直线与圆可以相切、相交、外切、内切。
2. 圆的性质:取点到圆心的距离相等;圆两点到圆心的连线,长度相等,角度相等;圆周上的点,到圆心两条连线的比值相等。
3. 圆心角:圆心角及其扇形的面积,与圆上两点的距离有关。
4. 关于圆的全等:两个半径相等的圆,它们的圆心角两端的线段的角度也相等;重心相等的圆,它们的圆心角也是相等的。
5. 关于圆的切线:圆上的点到圆心连线,为切线;圆上两点连线为切线;任一点到圆心的连线与任一点到圆上另外一点的连线的夹角为切线。
二、解题技巧
1. 图形分析法:根据题意绘制出合理的几何图形,对圆形的部分应尽量详细地描绘出来,综合分析各个部分的相互关系,以此判断圆形的计算结果。
2. 数字分析法:根据数据来分析圆形的特性,比如圆的半径是给定的,那么可以根据圆的性质和圆心角来推算其他参数的值;又如圆心角的角度是已知的,则可以推算出其它参数的值。
3. 结论法:圆周上的点,所到圆心的连线的比值都是相同的;圆心角的扇形面积和它的的圆心角的角度有关。
这些基本性质可以在解题中灵活地运用,通过比较不同扇形的面积来判断其可行的解,从
而推断出解题的具体值。
直线与圆的位置关系( 切线的判定与性质,十大题型)( 原卷版)
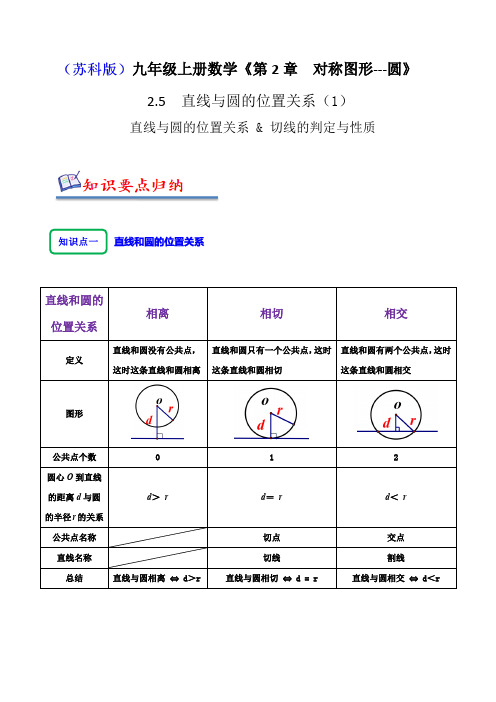
解题技巧提炼
本题主要考查了直线和圆的位置关系,解决此类问题的关键是根据圆心到直线的距离与半径的大小关系判断.
①d<r⇔直线和圆相交;②d=r⇔直线和圆相切;③d>r⇔直线和圆相离.
【变式1-1】(2023春•宁远县期中)已知⊙O的半径是10,圆心O到直线l的距离是13,则直线l与⊙O的位置关系是( )
【变式4-1】(2022•雁塔区校级模拟)如图,在等腰三角形ABC中,已知BC=4,AB=AC=3,若⊙C的半径为1,P为AB边上一动点,过点P作⊙C的切线PQ,切考)在平面直角坐标系内,以原点O为圆心,1为半径作圆,点
,过点P作该圆的一条切线,切点为A,则PA的最小值为( )
(1)r=4cm.(2)r=4.8cm.(3)r=6cm.
【例题2】(2022秋•江夏区校级期末)已知⊙O的半径等于5,圆心O到直线l的距离为4,那么直线l与⊙O的公共点的个数是( )
A.0B.1C.2D.无法确定
解题技巧提炼
直线和圆的位置关系与圆的公共点个数间的关系:
1、直线和圆相交⇔两个公共点,
【变式3-3】(2023•前郭县二模)如图,平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相交,则平移的距离d的取值范围是.
【变式3-4】Rt△ABC中,∠C=90°,AC=3,BC=4,若以点C为圆心,r为半径,且⊙C与斜边AB有唯一公共点,求半径r的取值范围.
【例题4】(2022秋•凉山州期末)点A是半径为2的⊙O上一动点,点O到直线MN的距离为3.点P是MN上一个动点.在运动过程中若∠POA=90°,则线段PA的最小值是.
解题技巧提炼
本题主要考查了根据直线和圆的位置关系中的相切来解决问题,结合勾股定理,添加适当的辅助线是解题的关键.利用“过直线外一点与直线上的所有连线中垂线段最短”求最值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与圆题型及做题技巧
一、直线与圆题型
1、求圆与直线的位置关系,即直线是否与圆相交,相交的情况有几种;
2、求直线与圆的交点;
3、求圆与直线的切线;
4、求直线与圆的关系,即圆是否在直线内部,圆是否完全包含在直线外面;
5、求直线上一点到圆的距离;
6、求圆上一点到直线的距离;
7、求圆心到直线的距离;
8、求圆的切点;
9、求圆的外切线;
10、求圆的内切线;
二、做题技巧
1、首先应该判断出圆与直线的位置关系,其次才能确定
解题思路;
2、要分析圆的参数方程和直线的参数方程,并将它们进
行比较;
3、从圆的数学定义出发,可以把问题转化为求解二元一
次方程组;
4、可以利用圆心到直线的距离公式求解;
5、可以利用圆上一点到直线的距离公式求解;
6、可以利用圆的切点求解,如果圆与直线不相交,可以
求出两个切点;
7、可以利用圆的外切线求解,此时可以求出一条外切线;
8、可以利用圆的内切线求解,此时可以求出一条内切线;
9、可以利用圆的半径求解,如果圆与直线不相交,可以
求出直线与圆的距离;
10、可以利用三角法求解,如果圆与直线不相交,可以求出直线与圆的距离。
总之,在做直线与圆的题目时,首先要分析出圆与直线的位置关系,然后根据圆和直线的数学定义,把问题转化为求解
二元一次方程组的形式,再利用相关公式解出相应的解,最后根据题目要求,得出结果。
