测量不确定度评定实例(完整资料).doc
不确定度评定实例分析

液态物料定量灌装机灌装量误差测量结果的不确定度评定与应用液态物料灌装机(以下简称“灌装机”)是一种将液态产品按预定量灌注到包装容器内的灌装设备,广泛应用于食品、药品、化工等生产领域,也是保证消费者和生产企业双方利益的重要计量器具。
因而正确开展灌装机灌装量误差测量结果的不确定度评定,对帮助企业了解、掌握灌装机灌装量得变化范围,减少企业损失,增加效益有着非常重要的意义。
一、概述1.测量依据JJG 687-2008《液态物料定量灌装机》检定规程2.测量条件温度:5℃~40℃,一次校准过程中校准介质的温差≦5℃。
3.测量标准器2级电子天平:8200g/0.01g ;密度测量装置:(0.0000~1.9999) g/cm 3;MPE :±0.0005 g/cm 3。
4.被测对象及其主要性能灌装机的最大允许误差为±2%(按灌装量标称值450ml 计,最大允许误差为 ±9ml)。
5.测量过程在规定的测量条件下,用2级电子天平、密度测量装置对灌装机在规定的预定灌装量点450ml 灌装量的实际质量值和校准介质的密度进行测量,灌装机灌装量标称值V 与盛装容器内校准介质的实际容量值V i (m i /ρ)比较之差值,为灌装机灌装量的绝对误差。
6.评定结果的使用在符合上述条件的情况下,对灌装量标称值为450ml 及其他规格预定灌装量标称值的其他灌装机灌装量测量结果的不确定度可采用本评定方法。
二、数学模型)]20(1[/t m V V V E i i -+-=-=βρ]式中:E -灌装量绝对误差,mL ;V -灌装量标称值,mL ;V i -第i 个盛装容器内的液体的实际容量,mL ;m i -第i 个盛装容器内的液体的实际质量,g ;ρ-液体平均密度,g/cm 3;β-灌装机的体膨胀系数,/℃;t -校准时液体的温度,℃。
三、输入量的标准不确定度评定1.输入量V 的标准不确定度u(V)的评定由于V 为灌装量的标称值,不随外界因素变化而变化,故其无不确定因素,所以 u(V)=02.输入量m i 的标准不确定度u(m i )的评定输入量m i 的不确定度主要来源于灌装机测量的重复性引入的标准不确定度分项u(i m )、2级电子天平最大允许误差引入的标准不确定度分项u(m Ⅱ)。
可见分光光度计的测量不确定度评定
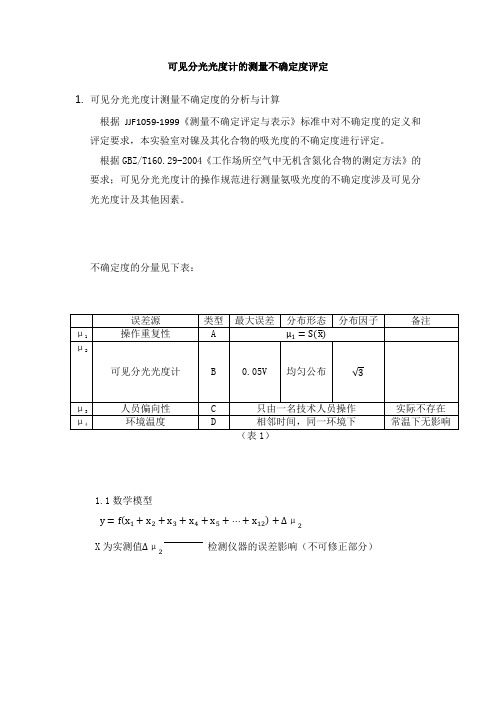
0.020
1.3测量不确定度的B类分量计算:
对应表1的B类不确定分量计算如下:
可见分光光度计说明书中所表明的最大误差是0.25nm,即a=0.25;取均匀分布k= ;
0.144
1.4合成不确定度
0.148
1.5扩展不确定度的评定:
不确定度的分量见下表:
误差源
类型
最大误差
分布形态
分布因子
备注
μ1
操作重复性
A
μ2
可见分光光度计
B
0.05V
均匀公布
μ3
人员偏向性
C
只由一名技术人员操作
实际不存在
μ4
环境温度
D
相邻时间,同一环境下
常温下无影响
(表1)
1.1数学模型
X为实测值 检测仪器的误差影响(不可修正部分)
1.2测量不确定的A类分量计算
单位:
测量次数 x1x2x3x4x5x6x7x8x9x10x11x12
实测值0.461 0.452 0.455 0.450 0.447 0.452 0.454 0.450 0.452 0.452 0.451 0.452
表2
(1)、12次观察结果的算术平均值:
0.452
(2)、计算样本标准偏差:0.035来自可见分光光度计的测量不确定度评定
1.可见分光光度计测量不确定度的分析与计算
根据JJF1059-1999《测量不确定评定与表示》标准中对不确定度的定义和评定要求,本实验室对镍及其化合物的吸光度的不确定度进行评定。
根据GBZ/T160.29-2004《工作场所空气中无机含氮化合物的测定方法》的要求;可见分光光度计的操作规范进行测量氨吸光度的不确定度涉及可见分光光度计及其他因素。
测量不确定度案例分析

标准不确定度A类评定的实例【案例】对一等活塞压力计的活塞有效面积检定中,在各种压力下,测得10次活塞有效面积与标准活塞面积之比l (由l的测量结果乘标准活塞面积就得到被检活塞的有效面积)如下:0。
250670 0。
250673 0.250670 0。
250671 0.250675 0。
250671 0。
250675 0.250670 0。
250673 0。
250670问l 的测量结果及其A 类标准不确定度。
【案例分析】由于n =10, l 的测量结果为l ,计算如下∑===n i i .l n l 125067201 由贝塞尔公式求单次测量值的实验标准差()612100521-=⨯=--=∑.n l l )l (s n i i由于测量结果以10次测量值的平均值给出,由测量重复性导致的测量结果l 的A 类标准不确定度为610630-=⨯=.)l (u n )l (s A 【案例】对某一几何量进行连续4次测量,得到测量值:0。
250mm 0.236mm 0.213mm 0。
220mm ,求单次测量值的实验标准差。
【案例分析】由于测量次数较少,用极差法求实验标准差.)()(i i x u CR x s ==式中,R-—重复测量中最大值与最小值之差;极差系数c及自由度ν可查表3-2表3-2极差系数c及自由度ν查表得c n =2.06mm ../mm )..()x (u CR )x (s i i 018006221302500=-=== 2)测量过程的A 类标准不确定度评定对一个测量过程或计量标准,如果采用核查标准进行长期核查,使测量过程处于统计控制状态,则该测量过程的实验标准偏差为合并样本标准偏差S P 。
若每次核查时测量次数n 相同,每次核查时的样本标准偏差为Si ,共核查k 次,则合并样本标准偏差S P 为k s s ki ip ∑==12此时S P 的自由度ν=(n —1)k .则在此测量过程中,测量结果的A 类标准不确定度为 n S A P u '=式中的n '为本次获得测量结果时的测量次数。
铠装热电偶测量结果不确定度评定

铠装热电偶测量结果不确定度评定1.校准方法校准依据: JJF 1262-2010《铠装热电偶校准规范》测量标准: 二等标准铂铑10-铂热电偶 ;2010型数字多用表,0.005级。
被测对象: 2级K 型铠装热电偶测量过程:采用双极比较法进行校准,将二等标准铂铑10-铂热电偶(以下简称标准偶)与被校偶工作端对齐捆扎后放入卧式管型检定炉内中心点,在校准点温度上进行比较,测量标准偶和被校铠装偶的热电动势值。
2.数学模型 补被标标标证被被e )()()(e -)()(+•+=t S t S t e t e t e (1))(被t e -—被校铠装偶在校准温度点t 附近测得的热电动势算术平均值,mV ; 标证e ——标准热电偶证书上校准温度点t 的热电动势值,mV ;)(标t e ——标准热电偶在校准温度点t 附近测得的热电动势算术平均值,mV ;)(标t S ,)(被t S ——标准热电偶、被校铠装偶在校准温度点的微分热电动势,μV/℃。
补e ——补偿导线修正值,mV 。
3.合成方差和灵敏系数[][][][]2补42标32标证22被12)()()()(e u c e u c e u c e u c u c +++= (2) 其中灵敏系数:)()(被被1t e t e C ∂∂= )()()()(标被标证被2t S t S t e t e C =∂∂=)()()()(标被标被3t t S t e t e C -=∂∂=)()(补被4t e t e C ∂= 4.计算标准不确定度分量(以K 型铠装电偶校准点400℃,微分电动势42.24μV/℃ 为例)4.1 被校铠装电偶输入量)(被t e 带来的不确定度)(被e u 输入量)(被t e 的标准不确定度)(被e u ,其来源有被校铠装偶的重复性测量、电测设备测量误差、炉内径向温场的不均匀性、炉温的波动、转换开关接触电势、参考端温度不等于0℃、补偿导线等。
不确定度评估实例

不确定度评估实例1、测量问题本次评定实验以物资(商品)检验所游标卡尺09059为测试量具,用游标卡尺测量结构长度270mm的长度ι。
已知卡尺的最大误差为1mm。
用6次测量的平均值作为测量结果。
卡尺的温度效应、弹性效应及其他不确定度来源均忽略不计。
2、数学模型卡尺上得到的读数χ即为测量结果,故得被测长度ι=χ。
但除了读数χ可能引入测量不确定度外,卡尺刻度误差对测量结果也会有影响。
由于卡尺的校准证书未给出其示值误差,因此只能根据其最大允许误差来估计它对测量结果的影响。
若卡尺刻度误差对测量结果的影响διS,则数学模型可以表示为ι=χ+διS式中διS的数学期望值为零,即Ε(διS)=0,但需考虑其不确定度,即μ(διS)≠0。
数学模型是相对的,即使对于同样的被测量,当要求的测量准确度不同时,需要考虑的测量不确定度来源也会有相应的增减,因此数学模型也会不同。
3、测量不确定度分量本测量共有两个不确定度分量,由读数的重复性引入的不确定度μ(χ)和卡尺刻度误差所引起的不确定度μ(διS)。
⑴读数χ的不确定度,μ1(ι)=μ(χ)6次测量结果分别为270、3mm270、1mm270mm271、4mm269、8mm271、2mm则6次测量结果的平均值为==270、47mm平均值的实验标准差为 s()==0、074mm故μ1(ι)=μ()=s()=0、074mm⑵卡尺误差引入的不确定度, μ2(ι)=μ(διS)由于证书未给出卡尺的示值误差,故卡尺刻度误差引入的不确定度由卡尺的最大允许误差得到。
已知卡尺的最大误差为1mm,并以矩形分布估计,于是μ2(ι)=μ(διS)==0、577mm下表给出不确定度分量汇总表符号栏中u1=s1 意为用实验标准s来表示不确定度,言外之意是该不确定度分量有A类评定得到的。
反之,对于未标u=s的不确定度分量,则表示是由B 类评定得到的。
这是经常采用的标明A类评定和B类评定不确定度分量的方法之一。
JJF1059.1-2012规程测量不确定度评定与表示(精编文档).doc

【最新整理,下载后即可编辑】JJF 中华人民共和国国家计量技术规范JJF1059.1-2012测量不确定度评定与表示Evaluation and Expressionof Uncertainty in Measurement2012-12-03 发布2013-06-03实施国家质量监督检验检疫总局发布测量不确定度评定与表示归口单位:全国法制计量管理计量技术委员会起草单位:江苏省计量科学研究院中国计量科学研究院北京理工大学国家质检总局计量司本规范委托全国法制计量管理计量技术委员会解释本规范起草人:叶德培赵峰(江苏省计量科学研究院)施昌彦原遵东(中国计量科学研究院)沙定国(北京理工大学)周桃庚(北京理工大学)陈红(国家质检总局计量司)目录引言1 范围2 引用文献3 术语和定义4 测量不确定度的评定方法4.1 测量不确定度来源分析4.2 测量模型的建立4.3 标准不确定度的评定4.4 合成标准不确定度的计算4.5 扩展不确定度的确定5 测量不确定度的报告与表示6.测量不确定度的应用附录A 测量不确定度评定举例(参考件)附录B t分布在不同概率p与自由度ν的)(νt值(t值)(补充件)p附录C 有关量的符号汇总(补充件)附录D 术语的英汉对照(参考件)1 引言本规范是对JJF1059-1999《测量不确定度评定与表示》的修订。
本次修订的依据是十多年来我国贯彻JJF1059-1999的经验以及最新的国际标准ISO/IEC Guide98-3-2008《测量不确定度第3部分:测量不确定度表示指南》(Uncertainty of measurement-Part 3:Guide to the Expression of Uncertainty in Measurement以下简称GUM),与JJF 1059-1999相比,主要修订内容有:--编写格式改为符合JJF1071-2010《国家计量校准规范编写规则》的要求。
测量不确定度评定实例和有关附录

直接测量方法不确定度评定实例直接测量方法是指“不必测量与被测量有函数关系的其他量,而能直接得到被测量值的测量方法”。
在测量程序中,有时为了作出相应的修正,需要进行补充测量或计算以确定影响量之值。
这种测量方法仍然是直接测量。
根据计量器具的示值,还需要通过查阅有关图或表以确定被测量之值的测量,也是直接测量。
直接测量是我们遇到的最多的也是最基本的测量。
通过测量与被测量有函数关系的其他量,按函数关系计算出被测量之值的简接测量方法是建立在直接测量的基础上的测量。
直接测量的不确定度来源主要包括:(1) 测量重复性,采用A类评定方法评定。
(2) 测量设备,包括测量设备的误差或不确定度,以及设备分分辩力(读数)误差,采用B类方法评定。
(3) 其他,参见第二章第三节。
直接测量方法的各个标准不确定度分量,包括影响量引入的标准不确定度分量,通常都是互不相关的,合成标准不确定度一般采用方和根方法计算。
【实例1】薄膜厚度测量不确定度评定一、概述1.1 目的评定软性塑料薄膜厚度测量结果的不确定度。
1.2 依据标准EN 71-1《欧洲玩具安全标准》。
1.3 使用的仪器设备数显千分表测厚仪,最大允许误差±3μm,分辩力1μm;千分表座平面度小于+0.6μm。
经检定合格。
1.4 测量程序将试样剪成(100×100)mm2,,平正放置在数显千分表测厚仪不锈钢材质的表座上。
测量试样对角线上10个等距离点的厚度,由该10个算术平均值给出被测量值。
1.5 不确定度评定结果的应用符合上述条件或十分接近上述条件的厚度测量的不确定度,一般可以参照本例方法评定。
二、数学模型本例属于直接测量,被测量值直接由测量仪器的示值给出h=l(8.1.1)式中:h——薄膜试样厚度,mm;l——数显千分表测厚仪示值,mm;三、 测量不确定度来源厚度h 测量的不确定度来源主要包括:①薄膜厚度h 测量重复性引起的标准不确定度u A ;②数显千分表测厚仪示值误差引入的标准不确定度u B ;③千分尺读数分辩力1μm 引入的标准不确定度,其区间半宽度0.5μm 比示值误差的区间半宽度3μm 小5倍,可以忽略不计;④,千分表座平面度小于+0.6μm ,比示值误差的区间半宽度3μm 小4倍,也可以忽略不计。
测量不确定度评定示例

测量不确定度评定示例一、类型1, 有明确的数学模型的经典测量的例子例1. 酸碱滴定不确定度的估计例2. 材料静拉伸强度测定的不确定度估计用1.0级拉力试验机测量圆柱形试件,以受控速率施加轴向拉力,在拉断试件时的静拉伸强度。
在温度和其它条件不变时,拉伸强度可表示为:24πF F A dσ== (1)式中:σ——静拉伸强度,N/mm 2A ——截面积,mm 2 ,对圆柱形试件而言2A=πd /4 d ——圆柱形试件直径,mm F ——拉力,N 由公式(1)有222()()()2c c c u u F u d F d σσ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦…………………………(2) 式(1)和(2)中各量的量值列于表1中。
表1 计算静拉伸强度的不确度的有关量值各量值不确定度的计算:(1)直径d 的测量及其标准不确定度u c (d )用直径计量仪器测定试件的直径为10.00mm 。
其不确定度来源,第一,持证上岗人员多次重复测量的标准偏差经计算为0.005mm ;第二,直径测量仪校准证书上给出在95%置信概率下校准不确定度为0.003mm ,按正态分布转化成标准不确定度为0.003/1.96=0.0015mm以上二项合成有()0.0052mmc ud ==故相对标准不确定度为:()0.00520.0005210.00c ud d==(2)用1.0级拉力试验机测量拉断试件时拉力及其标准不确定度u c (F )。
用1.0级拉力试验机测量拉断试件时拉力为40000N 。
其不确定度来源:第一,示值不确定度对于1.0级拉力试验机供应商说明为示值的±1.0%。
故相对标准不确定度按均匀分布则相对标准不确定度为20.010.5810-=⨯;第二,拉力试验机用0.3级标准测力仪校准,测力仪的相对不确定度为0.3%,按正态分布转化则校准引入的相对标准不确定度为0.003/1.96=0.15×10-2 ;第三,拉力试验机刻度盘量程上限为200kN ,最小分度为0.5kN ,持证上岗人员可估读到0.2分度,即±0.1kN ,本例在40kN 处拉断故±0.1kN/40kN=±2.5×10-3,按均匀分布转化,人员读数引入的相对标准不确定度为332.510 1.410--⨯=⨯,以上三项合成得:() 0.0062c u F F==按公式(2)有:222()0.0062(20.00052)c u σσ⎡⎤=+⨯⎢⎥⎣⎦故2() 3.2/m m c u N σ= 由(1)式有22440000509.3/m mπ10.00N σ⨯==⨯扩展不确定度,取k=2,则2()2 3.2 6.4/mmU N σ=⨯=,取1位有效数字则有2()7/m m U N σ=结果表示为2(5097)/m m N ±。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此文档下载后即可编辑
测量不确定度评定实例
一. 体积测量不确定度计算 1. 测量方法
直接测量圆柱体的直径D 和高度h ,由函数关系是计算出圆柱体的体积
2
4
D v π=
由分度值为0.01mm 的测微仪重复6次测量直径D 和高度h ,测得数据见下表。
表: 测量数据
计算: mm 0.1110h mm 80.010==,
D
32
mm 8.8064
==
h D V π
2. 不确定度评定
分析测量方法可知,体积V 的测量不确定度影响因素主要有直径和高度的重复测量引起的不确定度21u u ,和测微仪示值误差引起的不确定度3u 。
分析其特点,可知不确定度21u u ,应采用A 类评定方法,而不确定度3u 采用B 类评定方法。
①.直径D 的重复性测量引起的不确定度分量 直径D 的6次测量平均值的标准差: ()m m 0048.0=D s 直径D 误差传递系数: h D
D V 2
π=∂∂ 直径D 的重复性测量引起的不确定度分量:
()3177.0mm D s D
V
u =∂∂=
②.高度h 的重复性测量引起的不确定度分量
高度h 的6次测量平均值的标准差: ()m m 0026.0=h s 高度h 的误差传递系数: 4
2
D h V π=∂∂
高度h 的重复性测量引起的不确定度分量:
()3221.0mm h s h
V
u =∂∂=
③测微仪示值误差引起的不确定度分量
由说明书获得测微仪的示值误差范围0.005mm ±,按均匀分布,示值的标准不确定度
0.0029
q
u == 由示值误差引起的直径测量的不确定度
q D u D V u ∂∂=
3 由示值误差引起的高度测量的不确定度
q h u h
V u ∂∂=
3 由示值误差引起的体积测量的不确定度分量 ()()323233mm 04.1=+=h D u u u
3. 合成不确定度评定
()()()3232221mm 3.1=++=u u u u c 4. 扩展不确定度评定
当置信因子3=k 时,体积测量的扩展不确定度为 3mm 9.33.13=⨯==c ku U 5.体积测量结果报告
() m m .93.88063±=±=U V V
考虑到有效数字的概念,体积测量的结果应为 () m m 48073±=V
二.伏安法电阻测量不确定度计算 1. 测量方法:
通过测量电阻两端电压和所通过的电流,计算被测电阻。
电流通过1Ω标准电阻两端电压间接测量,数据见下表。
表: 测量数据
数字电压表的20V 量程的允许误差)0.015%FS 0.04%RD ( +±=∆,200mV 量程的允许误差)0.01%FS 0.03%RD ( +±=∆;标准电阻的准确度等级为0.01级。
计算公式: I
V R V I V N I
==
X R
电阻两端电压平均值828.018=V V V ,标准差()V 0024.0=V s
标准电阻两端电压平均值46.1135=I V mV ,标准差()mV 018.0=I V s 电流的平均值mA I 46.1135=; 标准电阻的标准不确定度()Ω==
00006.0100/3
01.0N R s
Ω===
80.133135146
.00828
.18R X I V V
2. 标准测量不确定度评定
①电阻两端电压重复测量引起的A 类不确定度分量
()Ω==∂∂=
018.0135146
.00024.01V s V R u ②电阻两端电压测量数字电压表允许误差引起的B 类不确定
度分量
数字电压表20V 档的允许误差引起的标准不确定度
V 006.03
20
0.015% 18.08280.04%3
0.015%FS
0.04%RD =⨯+⨯=
+=
BV u
电阻两端电压测量数字电压表允许误差引起的B 类不确定度分量
Ω==∂∂=
044.0135146
.0006.02BV u V R u ③电阻电流重复测量引起的A 类不确定度分量
电流重复性测量的A 类不确定度
()()()mA 018.018.0011=⨯==∂∂=
I I A R V s R V s V I I u
()()()
Ω=⨯⨯==∂=
- .0175010.018036146.103223I u I I u I u A A
④电流测量数字电压表允许误差引起的B 类不确定度分量 数字电压表200mV 档的允许误差引起的标准不确定度
m V
53.003
200
0.01% 146.1350.03%3
0.01%FS
0.03%RD =⨯+⨯=
+=
BI u
数字电压表允许误差引起的测量电流的B 类不确定度
()
()()mA .0360.000060146.113535.001 1 2
2
2
2
2
2
2=⎪⎭⎫ ⎝⎛⨯+⎪⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭
⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪
⎪⎭
⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=N N N BI N N N BI I B R R s R I
u R R s R I
u V I I u
()()
()()Ω=⨯⨯=⨯=∂∂=-.0360 10036.035146.10828.0183
2
24I u I V I u I R u B B
3. 合成不确定度评定
()()()()Ω=+++=
+++=06.0036.00175.0044.0018.0)(2
2222
4232221u u u u R u c
4. 扩展不确定度评定
当置信因子3=k 时,体积测量的扩展不确定度为 Ω=⨯== 18.006.03c ku U 5.电阻测量结果报告 () 18.080.133Ω±=±=U R R X X。
