人教版 5相交线与平行线专项练习(几何大题)
人教版七年级数学下册《第五章 相交线与平行线》练习题-附带答案
人教版七年级数学下册《第五章相交线与平行线》练习题-附带答案一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的．1．下列图形中∠1与∠2是对顶角的是A．B．C．D．【答案】C2．下列说法正确的是A．大小相等的两个角互为对顶角B．有公共顶点且相等的两个角是对顶角C．两角之和为180°则这两个角互为邻补角D．—个角的邻补角可能是锐角、钝角或直角【答案】D【解析】A．大小相等的两个角互为对顶角错误；B．有公共顶点且相等的两个角是对顶角；错误；C．两角之和为180°则这两个角互为邻补角错误；D．—个角的邻补角可能是锐角、钝角或直角正确．故选D．3．如图直线AB CD相交于点O所形成的∠1、∠2、∠3和∠4中一定相等的角有A．0对B．1对C．2对D．4对【答案】C4．如图直线AB CD相交于点O若∠1＋80°=∠BOC则∠BOC等于A．130°B．140°C．150°D．160°【答案】A【解析】因为∠1+∠BOC=180°∠1＋80°=∠BOC所以∠1+∠1+80°=180°解得：∠1=50°所以∠BOC=130°．故选A．二、填空题：请将答案填在题中横线上．5．如图所示AB与CD相交所成的四个角中∠1的邻补角是__________∠1的对顶角是__________.【答案】∠2和∠4；∠3【解析】根据对顶角和邻补角的定义解答注意两直线相交一个角的对顶角只有一个但邻补角有两个．由图形可知∠1的对顶角是∠3∠1的邻补角是∠2和∠4．6．如图是一把剪刀其中∠1=40°则∠2=_________其理由是_________．【答案】40°对顶角相等【解析】因为对顶角相等所以∠2=∠1=40°．故答案为：40°对顶角相等．三、解答题：解答应写出文字说明、证明过程或演算步骤．7．如图所示AB CD EF交于点O∠1=20°∠2=60°求∠BOC的度数．【解析】因为∠BOF=∠2=60°所以∠BOC=∠1+∠BOF=20°+60°=80°．8．如图直线AB CD相交于点O∠EOC=70°OA平分∠EOC求∠BOD的度数．9．探究题：（1）三条直线相交最少有_________个交点；最多有_________个交点画出图形并数出图形中的对顶角和邻补角的对数；（2）四条直线相交最少有_________个交点；最多有_________个交点画出图形并数出图形中的对顶角和邻补角的对数；（3）依次类推n条直线相交最少有_________个交点；最多有_________个交点对顶角有_________对邻补角有_________对．【解析】当直线同交于一点时只有一个交点；当直线两两相交且不过同一点时交点个数最多；根据对顶角与邻补角的定义找出即可．（1）三条直线相交最少有1个交点最多有3个交点如图：对顶角：6对邻补角：12对；。
人教版七年级数学下册第五章《相交线与平行线》同步练习(含详解)
第五章相交线与平行线5．1 相交线5．1.1 相交线基础题知识点1 认识邻补角和对顶角(1)有一条公共边，另一边互为反向延长线，具有这种位置关系的两个角互为邻补角．(2)有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角互为对顶角．1．(2018·贺州)如图，下列各组角中，互为对顶角的是( A )A．∠1和∠2B．∠1和∠3C．∠2和∠4D．∠2和∠52．下面四个图形中，∠1与∠2是邻补角的是( D )3．如图，AB与CD相交所成的四个角中，∠1的邻补角是∠2，∠4，∠1的对顶角是∠3．知识点2 邻补角和对顶角的性质(1)互为邻补角的两个角相加等于180°．(2)对顶角相等．4．(2017·河池)如图，点O在直线AB上，若∠BOC＝60°，则∠AOC的大小是( C )A．60° B．90° C．120° D．150°5．(2018·钦州期末)如图，已知∠1＝120°，则∠2的度数是( A )A．120°B．90°C．60°D．30°6．(教材P9复习题T9变式)如图，测角器测得工件(圆台)的角度是40度，其测量角的原理是对顶角相等．7．在括号内填写依据：如图，因为直线a ，b 相交于点O ， 所以∠1＋∠3＝180°(邻补角互补)， ∠1＝∠2(对顶角相等)．8．如图，直线AB ，CD 相交于点O ，∠EOC＝70°，OA 平分∠EOC，求∠BOD 的度数．解：因为OA 平分∠EOC，∠EOC＝70°， 所以∠AOC ＝12∠EOC＝35°.所以∠BOD＝∠AOC＝35°.易错点1 对对顶角的性质理解不透彻而判断失误 9．下列说法正确的有( B )①对顶角相等；②相等的角是对顶角；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不是对顶角，则这两个角不相等．A ．1个B ．2个C ．3个D ．4个易错点2 未给出图形，考虑不全而致错10．两条直线相交所成的四个角中，有两个角分别是(2x －10)°和(110－x)°，则x ＝40或80．中档题11．如图，三条直线l 1，l 2，l 3相交于一点，则∠1＋∠2＋∠3＝( C )A ．90°B ．120°C ．180°D ．360°12．如图，直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°，则∠AOC 的度数为( A )A．62° B．118°C．72° D．59°13．(2018·揭阳揭西县期末)如图所示，直线AB与CD相交于点O，OE平分∠BOC.若∠BOE＝60°，则∠AOC的度数为( A )A．60° B．30° C．120° D．45°14．如图，已知直线AB，CD，EF相交于点O.(1)∠AOD的对顶角是∠BOC，∠EOC的对顶角是∠DOF；(2)∠AOC的邻补角是∠AOD和∠BOC，∠EOB的邻补角是∠EOA和∠BOF．15．如图，直线a，b，c两两相交，∠1＝80°，∠2＝2∠3，则∠4＝140°．16．如图，直线a，b相交于点O，已知3∠1－∠2＝100°，则∠3＝130°．17．如图，直线AB，CD相交于点O，∠AOE＝∠BOE，OB平分∠DOF.若∠DOE＝50°，求∠DOF的度数．解：因为∠AOE＝∠BOE，且∠AOE＋∠BOE＝180°，所以∠AOE＝∠BOE＝90°.因为∠DOE＝50°，所以∠DOB＝∠BOE－∠DOE＝40°.因为OB 平分∠DOF，所以∠DOF＝2∠DOB＝80°.18．如图，l 1，l 2，l 3交于点O ，∠1＝∠2，∠3∶∠1＝8∶1，求∠4的度数．解：设∠1＝∠2＝x°，则∠3＝8x°. 由∠1＋∠2＋∠3＝180°，得 10x ＝180.解得x ＝18. 所以∠1＝∠2＝18°.所以∠4＝∠1＋∠2＝36°.综合题19．探究题：(1)三条直线相交，最少有1个交点，最多有3个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数； (2)四条直线相交，最少有1个交点，最多有6个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数； (3)依次类推，n 条直线相交，最少有1个交点，最多有n （n －1）2个交点，对顶角有n(n －1)对，邻补角有2n(n－1)对．解：(1)图略，对顶角有6对，邻补角有12对． (2)图略，对顶角有12对，邻补角有24对．5.1.2 垂线基础题知识点1 认识垂直如果两条直线相交所成的四个角中的任意一个角等于90°，那么这两条直线互相垂直．其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足．1．如图，OA⊥OB，若∠1＝55°，则∠2＝( A )A．35°B．40°C．45° D．60°2．(2018·来宾期末)如图，AB⊥CD于点O，EF为经过点O的一条直线，那么∠1与∠2的关系是( C )A．互为对顶角B．互补C．互余D．相等3．如图，已知直线AB，CD，EF相交于点O，AB⊥CD，∠DOE＝127°，求∠AOF的大小．解：因为AB⊥CD，所以∠DOB＝90°.又因为∠DOE＝127°，所以∠BOE＝∠DOE－∠DOB＝127°－90°＝37°.所以∠AOF＝∠BOE＝37°.知识点2 画垂线4．下列各图中，过直线l外一点P画l的垂线CD，三角板操作正确的是( D )知识点3 垂线的性质(1)在同一平面内，过一点有且只有一条直线与已知直线垂直．(2)连接直线外一点与直线上各点的所有线段中，垂线段最短．5．(2017·柳州)如图，经过直线l外一点A画l的垂线，能画出( A )A．1条B．2条C．3条D．4条6．(2018·佛山顺德区期末)如图是小希同学跳远时沙坑的示意图，测量成绩时先用皮尺从后脚印的点A处垂直拉至起跳线l的点B处，然后记录AB的长度，这样做的理由是( C )A．两点之间线段最短B．过两点有且只有一条直线C．垂线段最短D．过一点可以作无数条直线7．下面可以得到在如图所示的直角三角形中斜边最长的原理是( D )A．两点确定一条直线B．两点之间线段最短C．过一点有且只有一条直线和已知直线垂直D．垂线段最短8．下列说法正确的有( C )①在平面内，过直线上一点有且只有一条直线垂直于已知直线；②在平面内，过直线外一点有且只有一条直线垂直于已知直线；③在平面内，可以过任意一点画一条直线垂直于已知直线；④在平面内，有且只有一条直线垂直于已知直线．A．1个B．2个C．3个D．4个知识点4 点到直线的距离直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．9．(2017·北京)如图所示，点P到直线l的距离是( B )A．线段PA的长度B．线段PB的长度C．线段PC的长度D．线段PD的长度易错点未给出图形，考虑不周全致错10．已知OA⊥OC，过点O作射线OB，且∠AOB＝30°，则∠BOC的度数为120°或60°．中档题11．在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有一部分同学画出下列四种图形，请你数一数，错误的有( D )A．1个B．2个C．3个D．4个12．已知直线AB，CB，l在同一平面内，若A B⊥l，垂足为B，CB⊥l，垂足也为B，则符合题意的图形可以是( C )13．如图所示，下列说法不正确的是( C )A．点B到AC的垂线段是线段AB B．点C到AB的垂线段是线段ACC．线段AD是点D到BC的垂线段D．线段BD是点B到AD的垂线段14．(2018·贵港港南区期末)点P是直线l外一点，A，B，C为直线l上的三点，PA＝4 cm，PB＝5 cm，PC＝2 cm，则点P到直线l的距离( C )A．小于2 cm B．等于2 cm C．不大于2 cm D．等于4 cm15．如图，当∠1与∠2满足条件∠1＋∠2＝90°时，OA⊥OB.16．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM.若∠AOM＝35°，则∠CON的度数为55°．17．如图，已知DO ⊥CO，∠1＝36°，∠3＝36°. (1)求∠2的度数；(2)AO 与BO 垂直吗？说明理由．解：(1)因为DO⊥CO，所以∠DOC＝90°.因为∠1＝36°，所以∠2＝90°－36°＝54°. (2)AO⊥BO.理由如下：因为∠3＝36°，∠2＝54°， 所以∠3＋∠2＝90°. 所以AO⊥BO.18．如图，两直线AB ，CD 相交于点O ，OE 平分∠BOD，∠AOC∶∠AOD＝7∶11. (1)求∠COE 的度数；(2)若OF⊥OE，求∠COF 的度数．解：(1)因为∠AOC∶∠AOD＝7∶11，∠AOC＋∠AOD＝180°， 所以∠AOC＝70°，∠AOD＝110°. 所以∠BOD＝∠AOC＝70°， ∠BOC＝∠AOD＝110°. 又因为OE 平分∠BOD，所以∠BOE＝∠DOE＝12∠BOD＝35°.所以∠COE＝∠BOC＋∠BOE＝110°＋35°＝145°. (2)因为OF⊥OE，所以∠FOE＝90°.所以∠FOD＝∠FOE－∠DOE＝90°－35°＝55°. 所以∠COF＝180°－∠FOD＝180°－55°＝125°.5.1.3 同位角、内错角、同旁内角基础题知识点认识同位角、内错角、同旁内角如图，直线AB，CD与EF相交．(1)图中∠1和∠2分别在直线AB，CD的同一方(或上方)，并且都在直线EF的同侧(或右侧)，具有这样位置关系的一对角叫做同位角；(2)图中∠2和∠8都在直线AB，CD之间，并且分别在直线EF的两侧，具有这样位置关系的一对角叫做内错角；(3)图中∠2和∠7都在直线AB，CD之间，且都在直线EF的同一旁(或右侧)，具有这样位置关系的一对角叫做同旁内角．1．(2017·玉林)如图，直线a，b被c所截，则∠1与∠2是( B )A．同位角B．内错角C．同旁内角D．邻补角2．(2017·柳州期末)如图，与∠1是同位角的是( C )A．∠2 B．∠3C．∠4 D．∠53．如图，与∠1是同旁内角的是( D )A．∠2 B．∠3C．∠4 D．∠54．(2018·广州)如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是( B )A．∠4，∠2B．∠2，∠6 C．∠5，∠4D．∠2，∠45．如图，下列说法错误的是( D )A．∠A与∠EDC是同位角B．∠A与∠ABF是内错角C．∠A与∠ADC是同旁内角D．∠A与∠C是同旁内角6．如图，若∠1＝∠2，则在①∠3和∠2；②∠4和∠2；③∠3和∠6；④∠4和∠8中，相等的有( C )A．1对B．2对C．3对D．4对7．看图填空：(1)∠1和∠3是直线AB，BC被直线AC所截得的同旁内角；(2)∠1和∠4是直线AB，BC被直线AC所截得的同位角；(3)∠B和∠2是直线AB，AC被直线BC所截得的同位角；(4)∠B和∠4是直线AC，BC被直线AB所截得的内错角．8．如图，如果∠2＝100°，那么∠1的同位角等于80°，∠1的内错角等于80°，∠1的同旁内角等于100°．中档题9．(2018·华南师大附中月考)在下列四个图中，∠1与∠2是同位角的图是( B )图①图②图③图④A．①② B．①③C．②③ D．③④10．如图，属于内错角的是( D )A．∠1和∠2 B．∠2和∠3C．∠1和∠4 D．∠3和∠411．如图，下列说法错误的是( B )A．∠A和∠C是同旁内角B．∠1和∠3是同位角C．∠2和∠3是内错角D．∠3和∠B是同旁内角12．如图，∠ABC与∠EAD是同位角；∠ADB与∠DBC，∠EAD是内错角；∠ABC与∠DAB，∠BCD是同旁内角．13．根据图形填空：(1)若直线ED，BC被直线AB所截，则∠1和∠2是同位角；(2)若直线ED，BC被直线AF所截，则∠3和∠4是内错角；(3)∠1和∠3是直线AB，AF被直线ED所截构成的内错角；(4)∠2和∠4是直线AB，AF被直线BC所截构成的同位角．14．根据图形说出下列各对角是什么位置关系？(1)∠1和∠2；(2)∠1和∠7；(3)∠3和∠4；(4)∠4和∠6；(5)∠5和∠7.解：(1)∠1和∠2是同旁内角；(2)∠1和∠7是同位角；(3)∠3和∠4是内错角；(4)∠4和∠6是同旁内角；(5)∠5和∠7是内错角．15．如图，如果内错角∠1与∠5相等，那么与∠1相等的角还有吗？与∠1互补的角有吗？如果有，请写出来，并说明你的理由．解：∠1＝∠2，与∠1互补的角有∠3和∠4.理由：因为∠1＝∠5，∠5＝∠2，所以∠1＝∠2.因为∠1＝∠5，且∠5与∠3或∠4互补，所以与∠1互补的角有∠3和∠4.综合题16．探究题：(1)如图1，两条水平的直线被一条竖直的直线所截，同位角有4对，内错角有2对，同旁内角有2对；图1 图2(2)如图2，三条水平的直线被一条竖直的直线所截，同位角有12对，内错角有6对，同旁内角有6对；(3)根据以上探究的结果，n(n为大于1的整数)条水平直线被一条竖直直线所截，同位角有2n(n－1)对，内错角有n(n－1)对，同旁内角有n(n－1)对．(用含n的式子表示)5.2 平行线及其判定5．2.1 平行线基础题知识点1 认识平行在同一平面内，两条不相交的直线互相平行．1．下列说法中，正确的是( D )A．平面内，没有公共点的两条线段平行B．平面内，没有公共点的两条射线平行C．没有公共点的两条直线互相平行D．互相平行的两条直线没有公共点2．在同一平面内的两条不重合的直线的位置关系( C )A．有两种：垂直或相交B．有三种：平行，垂直或相交C．有两种：平行或相交D．有两种：平行或垂直3．在同一平面内，直线a与b满足下列条件，把它们的位置关系填在后面的横线上．(1)a与b没有公共点，则a与b平行；(2)a与b有且只有一个公共点，则a与b相交；(3)a与b有两个及以上公共点，则a与b重合．4．如图，完成下列各题：(1)用直尺在网格中完成：①画出直线AB的一条平行线；②经过点C画直线垂直于CD；(2)用符号表示上面①、②中的平行、垂直关系．解：(1)如图所示．(2)EF∥AB，MC⊥CD.知识点2 平行公理及其推论(1)经过直线外一点，有且只有一条直线与这条直线平行．(2)如果两条直线都与第三条直线平行，那么这两条直线也互相平行，即：如果a∥b，b∥c，那么a∥c.5．若直线a∥b，b∥c，则a∥c的依据是( D )A．平行公理B．等量代换C．等式的性质D．平行于同一条直线的两条直线平行6．点P，Q都是直线l外的点，下列说法正确的是( D )A．连接PQ，则PQ一定与直线l垂直B．连接PQ，则PQ一定与直线l平行C．连接PQ，则PQ一定与直线l相交D．过点P只能画一条直线与直线l平行7．如图，PC∥AB，QC∥AB，则点P，C，Q在一条直线上．理由是经过直线外一点，有且只有一条直线与这条直线平行．8．如图，P，Q分别是直线EF外两点．(1)过点P画直线AB∥EF，过点Q画直线CD∥EF；(2)AB与CD有怎样的位置关系？为什么？解：(1)如图．(2)AB∥CD.理由：因为AB∥EF，CD∥EF，所以AB∥CD.易错点对平行线的有关概念及公理理解不清9．(2017·玉林北流市期中)下列说法中，正确的有( A )①过一点有无数条直线与已知直线平行；②经过直线外一点有且只有一条直线与已知直线平行；③如果两条线段不相交，那么它们就平行；④如果两条直线不相交，那么它们就平行．A．1个B．2个C．3个D．4个中档题10．如图，AB∥CD，EF∥AB，AE∥MN，BF∥MN，由图中字母标出的互相平行的直线共有( C )A．4组B．5组C．6组D．7组11．如图，因为直线AB，CD相交于点P，AB∥EF，所以CD不平行于EF.理由是经过直线外一点，有且只有一条直线与这条直线平行．12．在同一平面内，一条直线和两条平行线中的一条直线相交，那么这条直线与平行线中的另一条直线必相交．13．(教材P17习题T11变式)观察下图所示的长方体，回答下列问题．(1)用符号表示两棱的位置关系：A1B1∥AB，AA1⊥AB，A1D1⊥C1D1，AD∥BC；(2)AB与B1C1所在的直线不相交，它们不是平行线(填“是”或“不是”)．由此可知，在同一平面内，两条不相交的直线才是平行线．14．如图，在∠AOB内有一点P.(1)过点P画l1∥OA；(2)过点P画l2∥OB；(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系．解：(1)(2)如图所示．(3)l1与l2的夹角有两个：∠1，∠2.量得∠1＝∠O，∠2＋∠O＝180°，所以l1与l2的夹角与∠O相等或互补．15．如图，取一张长方形的硬纸板ABCD，将硬纸板ABCD对折使CD与AB重合，EF为折痕．把长方形ABFE平放在桌面上，另一个面CDEF无论怎么改变位置总有CD∥AB存在，你知道为什么吗？解：因为AB∥EF，CD∥EF，所以CD∥AB.综合题16．利用直尺画图：(1)利用图1中的网格，过点P画直线AB的平行线和垂线；(2)在图2的网格中画一个四边形，满足：①两组对边互相平行；②任意两个顶点都不在一条网格线上；③四个顶点都在格点上．解：(1)如图所示．CD∥AB，PQ⊥AB.(2)如图所示．四边形ABCD是符合条件的四边形．5.2.2 平行线的判定基础题知识点1 同位角相等，两直线平行1．(2017·玉林陆川县期末)如图，给出了过直线外一点画已知直线的平行线的方法，其依据是( A )A．同位角相等，两直线平行B．内错角相等，两直线平行C．同旁内角互补，两直线平行D．两直线平行，同位角相等2．(2017·绥化)如图，直线AB，CD被直线EF所截，∠1＝55°，下列条件中能判定AB∥CD的是( C )A．∠2＝35°B．∠2＝45°C．∠2＝55°D．∠2＝125°3．(教材P21例2变式)已知a，b，c为平面内三条不同的直线，若a⊥b，c⊥b，则a与c的位置关系是平行．4．如图，∠3与∠1互余，∠3与∠2互余．试说明：AB∥CD.解：∵∠3与∠1互余，∠3与∠2互余，∴∠1＝∠2.∴AB∥CD(同位角相等，两直线平行)．知识点2 内错角相等，两直线平行5．(2018·深圳龙岗区一模)如图，能判定AB∥CD的条件是( A )A．∠A＝∠ACD B．∠A＝∠DCE C．∠B＝∠ACB D．∠B＝∠AC D6．如图，请在括号内填上正确的理由：∵∠DAC＝∠C(已知)，∴AD∥BC(内错角相等，两直线平行)．7．如图，∠BAD＝∠DCB，∠BAC＝∠DCA，试说明：AD∥BC.解：∵∠BAD＝∠DCB，∠BAC＝∠DCA(已知)，∴∠BAD－∠BAC＝∠DCB－∠DCA(等式的性质)，即∠DAC＝∠BCA．∴AD∥BC(内错角相等，两直线平行)．知识点3 同旁内角互补，两直线平行8．如图，已知∠1＝70°，要使AB∥CD，则须具备的另一个条件是( C )A．∠2＝70° B．∠2＝100°C．∠2＝110° D．∠3＝110°9．如图，装修工人向墙上钉木条．若∠2＝100°，要使木条b与a平行，则∠1的度数等于80°．10．如图，已知∠ACD＝70°，∠ACB＝60°，∠ABC＝50°.试说明：AB∥CD.解：∵∠ACD＝70°，∠ACB＝60°，∴∠BCD＝130°.∵∠ABC＝50°，∴∠BCD＋∠ABC＝180°.∴AB∥CD(同旁内角互补，两直线平行)．易错点不能准确识别截线与被截线，从而误判两直线平行11．(教材P36复习题T8(1)变式)(2018·贵港桂平期末)如图，点E在AC的延长线上，有下列条件：①∠1＝∠2；②∠3＝∠4；③∠A＝∠DCE；④∠D＝∠DCE；⑤∠A＋∠ABD＝180°；⑥∠A＋∠ACD＝180°，其中能判定AB∥CD 的是①③⑥．中档题12．(2018·郴州)如图，直线a，b被直线c所截，下列条件中，不能判定a∥b的是( D )A．∠2＝∠4 B．∠1＋∠4＝180° C．∠5＝∠4 D．∠1＝∠313．如图，下列说法错误的是( C )A．若a∥b，b∥c，则a∥c B．若∠1＝∠2，则a∥cC．若∠3＝∠2，则b∥c D．若∠3＋∠5＝180°，则a∥c14．(2018·湘潭)如图，点E是AD延长线上一点，如果添加一个条件，使BC∥AD，则可添加的条件为答案不唯一，如：∠C＝∠CDE．(任意添加一个符合题意的条件即可)15．如图，用几何语言表示下列句子．(1)因为∠1和∠B相等，根据“同位角相等，两直线平行”，所以DE和BC平行；(2)因为∠1和∠2相等，根据“内错角相等，两直线平行”，所以AB和EF平行；(3)因为∠BDE和∠B互补，根据“同旁内角互补，两直线平行”，所以DE和BC平行．解：(1)∵∠1＝∠B(已知)，∴DE∥BC(同位角相等，两直线平行)．(2)∵∠1＝∠2(已知)，∴EF∥AB(内错角相等，两直线平行)．(3)∵∠BDE＋∠B＝180°(已知)，∴DE∥BC(同旁内角互补，两直线平行)．16．(2018·湛江廉江市期末)完成下面的推理．如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.完成推理过程：∵BE 平分∠ABD(已知)，∴∠ABD＝2∠α(角平分线的定义)． ∵DE 平分∠BDC(已知)，∴∠BDC＝2∠β (角平分线的定义)．∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)(等量代换)． ∵∠α＋∠β＝90°(已知)，∴∠ABD＋∠BDC＝180°(等量代换)． ∴AB∥CD(同旁内角互补，两直线平行)．17．如图，点B 在AC 上，BD⊥BE，∠1＋∠C＝90°，问射线CF 与BD 平行吗？试用两种方法说明理由．解：CF∥BD.方法一：∵BD⊥BE， ∴∠DBE＝90°. ∴∠1＋∠2＝90°. ∵∠1＋∠C＝90°， ∴∠2＝∠C.∴CF∥BD(同位角相等，两直线平行)． 方法二：∵BD⊥BE，∴∠DBE＝90°. ∵∠1＋∠C＝90°，∴∠C＋∠DBC＝∠1＋∠DBE＋∠C＝90°＋90°＝180°. ∴CF∥BD(同旁内角互补，两直线平行)．18．如图，直线EF 分别与直线AB ，CD 相交于点P 和点Q ，PG 平分∠APQ ，QH 平分∠DQP，并且∠1＝∠2，说出图中哪些直线平行，并说明理由．解：PG∥QH，AB∥CD.∵PG 平分∠APQ，QH 平分∠DQP，∴∠1＝∠GPQ＝12∠APQ，∠PQH＝∠2＝12∠PQD.又∵∠1＝∠2，∴∠GPQ＝∠PQH，∠APQ＝∠PQD.∴PG∥QH，AB∥CD(内错角相等，两直线平行)．综合题19．如图，AB⊥BD 于点B ，CD⊥BD 于点D ，∠1＋∠2＝180°，试问CD 与EF 平行吗？为什么？解：CD∥EF.理由如下：∵AB⊥BD，CD⊥BD，∴∠ABD＝∠BDC＝90°.∴∠ABD＋∠BDC＝180°.∴AB∥CD(同旁内角互补，两直线平行)．∵∠1＋∠2＝180°，∴AB∥EF(同旁内角互补，两直线平行)．∴CD∥EF(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)．周周练(5.1～5.2)(时间：45分钟满分：100分)一、选择题(每小题4分，共32分)1．邻补角是指( D )A．和为180°的两个角B．有一条公共边且相等的两个角C．有公共顶点且互补的两个角D．有公共顶点且有一条公共边，另一边互为反向延长线的两个角2．如图，∠1和∠2是对顶角的是( B )3．如图，直线AB，CD被EF所截，下列说法正确的有( C )①∠3与∠5是内错角；②∠2与∠7是同位角；③∠4与∠5是同旁内角；④图中有4对同位角，2对内错角，2对同旁内角；⑤∠1与∠7是内错角．A．1个B．2个C．3个D．4个4．下列说法错误的是( C )A．两条直线相交，有一个角是直角，则两条直线互相垂直B．若互为对顶角的两角之和为180°，则两直线互相垂直C．两直线相交，所构成的四个角中，若有两个角相等，则两直线互相垂直D．在同一平面上，过点A作直线l的垂线，这样的垂线只有一条5．如图，直线AB⊥CD于点O，直线EF经过点O，若∠1＝26°，则∠2的度数是( B )A．26° B．64°C．54° D．以上都不对6．下列说法错误的是( A )A．过一点有且只有一条直线与已知直线平行B．平行于同一条直线的两条直线平行C．若a∥b，b∥c，c∥d，则a∥dD．同一平面内，若一条直线与两平行线中的一条相交，则它也和另一条相交7．如图，∠ACB＝90°，CD⊥AB，垂足为D，则下面的结论中，不正确的是( D )A．线段AC的长度是点A到BC的距离B．CD与AB互相垂直C．AC与BC互相垂直D．点B到AC的垂线段是线段CA8．(2017·深圳)下列选项中，哪个不可以得到l1∥l2？( C )A．∠1＝∠2 B．∠2＝∠3C．∠3＝∠5 D．∠3＋∠4＝180°二、填空题(每小题4分，共24分)9．如图，已知∠1＋∠2＝100°，则∠3＝130°．10．如图，已知OA⊥OB，OC⊥OD，∠AOC＝27°，则∠BOD的度数是153°．11．如图，把小河里的水引到田地A处就作AB⊥l，垂足为B，沿AB挖水沟，水沟最短．理由是垂线段最短．12．如图，在同一平面内，OA⊥l，OB⊥l，垂足为O，则OA与OB重合的理由是同一平面内，过一点有且只有一条直线与已知直线垂直．13．如图，已知∠C＝105°，增加一个条件答案不唯一，如∠BEC＝75°或∠AEC＝105°，使得AB∥CD.14．如图，AB与BC被AD所截得的内错角是∠1和∠3；DE与AC被直线AD所截得的内错角是∠2和∠4；图中∠4的内错角是∠5和∠2．三、解答题(共44分)15．(6分)完成下面的推理过程：如图，CB平分∠ACD，∠1＝∠3.试说明：AB∥CD.解：∵CB平分∠ACD，∴∠1＝∠2(角平分线的定义)．∵∠1＝∠3，∴∠2＝∠3．∴AB∥CD(内错角相等，两直线平行)．16．(6分)如图，直线AO，BO交于点O，过点P作PC⊥AO于点C，PD⊥BO于点D，画出图形．解：作∠ACP＝90°，作∠PDB＝90°，则直线PC，PD即为所求．17．(6分)如图，已知∠OEB＝130°，∠FOD＝25°，OF平分∠EOD，试说明：AB∥CD.解：∵OF平分∠EOD，∠FOD＝25°，∴∠EOD＝2∠FOD＝50°.又∵∠OEB＝130°，∴∠OEB＋∠EOD＝180°.∴AB∥CD(同旁内角互补，两直线平行)．18．(8分)如图，已知直线l1，l2，l3被直线l所截，∠α＝105°，∠β＝75°，∠γ＝75°，运用已知条件，你能找出哪两条直线是平行的吗？若能，请写出理由．解：l1∥l2∥l3.理由：∵∠1＝∠β，∠β＝75°，∴∠1＝75°.∵∠α＝105°，∴∠α＋∠1＝180°.∴l1∥l2(同旁内角互补，两直线平行)．∵∠β＝75°，∠γ＝75°，∴∠β＝∠γ.∴l2∥l3(内错角相等，两直线平行)．∴l1∥l2∥l3.19．(8分)如图，AB和CD交于点O，OD平分∠BOF，OE⊥CD于点O，∠AOC＝40°，求∠EOF的度数．解：∵AB，CD相交于点O，∴∠BOD＝∠AOC＝40°.∵OD平分∠BOF，∴∠DOF＝∠BOD＝40°.∵OE⊥CD，∴∠EOD＝90°.∴∠EOF＝∠EOD＋∠DOF＝130°.20．(10分)如图，要判定AB∥CD，需要哪些条件？根据是什么？解：①若考虑截线AD，则需∠D＋∠DAB＝180°，根据是同旁内角互补，两直线平行．②若考虑截线AE，则需∠CEA＋∠EAB＝180°，根据是同旁内角互补，两直线平行或∠DEA＝∠EAB，根据是内错角相等，两直线平行．③若考虑截线AC，则需∠DCA＝∠CAB，根据是内错角相等，两直线平行．④若考虑截线FC，则需∠DCF＋∠AFC＝180°，根据是同旁内角互补，两直线平行或∠DCF＝∠BFC，根据是内错角相等，两直线平行．⑤若考虑截线BC，则需∠DCB＋∠B＝180°，根据是同旁内角互补，两直线平行．5.3 平行线的性质5．3.1 平行线的性质基础题知识点1 平行线的性质平行线的性质：性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补．1．(2018·桂林)如图，直线a，b被直线c所截，a∥b，∠1＝60°，则∠2的度数是( B )A．120°B．60°C．45°D．30°2．(2018·绵阳)如图，有一块含有30°角的直角三角板的两个顶点放在直尺的对边上，如果∠2＝44°，那么∠1的度数是( C )A．14° B．15°C．16° D．17°3．如图，在三角形ABC中，∠B＝40°，过点C作CD∥AB，∠ACD＝65°，则∠ACB的度数为( D )A．60°B．65°C．70°D．75°4．如图，平行线AB，CD被直线AE所截，∠1＝50°，则∠A＝50°．5．如图，AB∥CD，∠BAF＝115°，则∠ECF的度数为65°．6．如图，EF∥BC，AC平分∠BAF，∠B＝80°.求∠C的度数．解：∵EF∥BC，∴∠BAF＝180°－∠B＝100°(两直线平行，同旁内角互补)． ∵AC 平分∠BAF ， ∴∠CAF＝12∠BAF＝50°.∵EF∥BC，∴∠C＝∠CAF＝50°(两直线平行，内错角相等)．知识点2 平行线性质的应用7．某商品的商标可以抽象为如图所示的三条线段，若AB∥CD，∠EAB＝45°，则∠FDC 的度数是( B )A ．30°B ．45°C ．60°D ．75° 8．一只因损坏而倾斜的椅子，从背后看到的形状如图所示，其中两组对边的平行关系没有发生变化．若∠1＝76°，则∠2的度数是( C )A ．76°B ．86°C ．104°D ．114°9．如图，在A ，B 两地挖一条笔直的水渠，从A 地测得水渠的走向是北偏西42°，A ，B 两地同时开工，B 地所挖水渠走向应为南偏东42°．10．如图，某次考古发掘出的一块梯形残缺玉片，工作人员从玉片上量得∠A＝115°，∠D＝100°，已知梯形的两底AD∥BC，请你帮助工作人员求出另外两个角的度数，并说明理由．解：∵AD∥BC，∠A＝115°，∠D＝100°， ∴∠B＝180°－∠A＝180°－115°＝65°， ∠C＝180°－∠D ＝180°－100°＝80°.易错点误用平行线的性质11．已知∠1与∠2是同旁内角，若∠1＝60°，则∠2的度数是( D )A．60° B．120°C．60°或120° D．不能确定中档题12．(2018·汕头澄海区一模)如图，点P是∠AOB的边OA上一点，PC⊥OB于点C，PD∥OB，∠OPC＝35°，则∠APD 的度数是( B )A．60°B．55°C．45°D．35°13．将一直角三角板与两边平行的纸条如图所示放置，下列结论：①∠1＝∠2；②∠3＝∠4；③∠2＋∠4＝90°；④∠4＋∠5＝180°.其中正确的有( D )A．1个B．2个C．3个D．4个14．(2018·梧州岑溪市期末)如图是一汽车探照灯的纵剖面，从位于O点的灯泡发出的两束光线OB，OC经过灯碗反射以后平行射出．若∠ABO＝α，∠DCO＝β，则∠BOC的度数是( A )A．α＋βB．180°－α C.12(α＋β)D．90°＋(α＋β)15．(2018·柳州期末)如图，AB∥CD∥EF，则下列四个等式中一定成立的有( A )①∠2＋∠3＝180°；②∠2＝∠3；③∠1＋∠3＝180°；④∠2＋∠3－∠1＝180°.A．1个B．2个C．3个D．4个16．(2017·柳州期末)如图，已知AB∥CD，BC∥ED，请你猜想∠B与∠D之间具有什么数量关系，并说明理由．解：猜想：∠B＋∠D＝180°.理由如下：∵AB∥CD，∴∠B＝∠C(两直线平行，内错角相等)．∵BC∥ED，∴∠C＋∠D＝180°(两直线平行，同旁内角互补)． ∴∠B＋∠D＝180°.17．(2017·南宁马山县期末)如图，CD∥AB，OE 平分∠AOD，OF⊥OE，∠D＝50°，求∠BOF 的度数．解：∵CD∥AB，∴∠AOD＝180°－∠D＝180°－50°＝130°. ∵OE 平分∠AOD，∴∠EOD＝12∠AOD＝12×130°＝65°.∵OF⊥OE，∴∠DOF＝90°－∠EOD＝90°－65°＝25°.∴∠BOF＝180°－∠AOD－∠DOF＝180°－130°－25°＝25°.综合题18．阅读下列解答过程：如图甲，AB∥CD，探索∠P 与∠A，∠C 之间的关系．解：过点P 作PE∥AB. ∵AB∥CD，∴PE∥AB∥C D(平行于同一条直线的两条直线互相平行)． ∴∠1＋∠A＝180°(两直线平行，同旁内角互补)， ∠2＋∠C＝180°(两直线平行，同旁内角互补)． ∴∠1＋∠A＋∠2＋∠C＝360°. 又∵∠APC＝∠1＋∠2， ∴∠APC＋∠A＋∠C＝360°.如图乙和图丙，AB∥CD，请根据上述方法分别探索两图中∠P 与∠A，∠C 之间的关系． 解：如图乙，过点P 作PE∥AB. ∵AB∥CD(已知)，∴PE∥AB∥CD(平行于同一条直线的两条直线平行)．∴∠A＝∠EPA，∠EPC＝∠C(两直线平行，内错角相等)． ∵∠APC＝∠EPA＋∠EPC，∴∠APC＝∠A＋∠C(等量代换)． 如图丙，过点P 作PF∥AB.∴∠FPA＝∠A(两直线平行，内错角相等)． ∵AB∥CD(已知)，∴PF∥CD(平行于同一条直线的两条直线平行)．∴∠FPC＝∠C(两直线平行，内错角相等)．∵∠FPC－∠FPA＝∠APC，∴∠C－∠A＝∠APC(等量代换)．5.3.2 命题、定理、证明基础题知识点1 命题的定义及结构判断一件事情的语句叫做命题，命题常可以写成“如果……那么……”的形式，“如果”后面接的部分是题设，“那么”后面接的部分是结论．1．(2018·玉林陆川县期末)下列语句不是命题的是( A )A．画两条相交直线B．互补的两个角之和是180°C．两点之间线段最短D．相等的两个角是对顶角2．把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是如果两条直线垂直于同一条直线，那么这两条直线平行．3．把下列命题改写成“如果……那么……”的形式，并分别指出它们的题设和结论：(1)两点确定一条直线；(2)同角的补角相等；(3)两个锐角互余．解：(1)如果在平面上有两个点，那么过这两个点确定一条直线．题设：在平面上有两个点；结论：过这两个点确定一条直线．(2)如果两个角是同一个角的补角，那么它们相等．题设：两个角是同一个角的补角；结论：这两个角相等．(3)如果两个角是锐角，那么这两个角互余．题设：两个角是锐角；结论：这两个角互余．知识点2 真假命题及其证明(1)题设成立，并且结论一定成立的命题叫做真命题；题设成立，不能保证结论一定成立的命题叫做假命题．(2)经过推理证实为正确并可以作为推理的依据的真命题叫做定理．很多情况下，一个命题的正确性需要经过推理，才能做出判断，这个推理的过程叫做证明．4．(2017·柳州期末)下列命题是真命题的是( C )A．同位角相等B．有且只有一条直线与已知直线垂直C．垂线段最短D．直线外一点到这条直线的垂线段，叫做点到直线的距离5．下列命题中，是假命题的是( A )A．相等的角是对顶角B．若|x|＝3，则x＝±3C．同一平面内，两条直线的位置关系只有相交和平行两种D．两点确定一条直线6．如图，BD平分∠ABC，若∠BCD＝70°，∠ABD＝55°.求证：CD∥AB.证明：∵BD 平分∠ABC，∠ABD＝55°， ∴∠ABC＝2∠ABD＝110°. 又∵∠BCD＝70°，∴∠ABC＋∠BCD＝180°.∴CD∥AB(同旁内角互补，两直线平行)．7．如图，如果∠1＝∠2，那么AB∥CD，这个命题是真命题吗？若不是，请你再添加一个条件，使该命题成为真命题，并说明理由．解：假命题，添加BE∥DF. ∵BE∥DF，∴∠EBD＝∠FDN(两直线平行，同位角相等)． ∵∠1＝∠2，∴∠EBD－∠1＝∠FDN－∠2. ∴∠ABD＝∠CDN.∴AB∥CD(同位角相等，两直线平行)．中档题8．(2017·无锡)对于命题“若a 2>b 2，则a>b.”下面四组关于a ，b 的值中，能说明这个命题是假命题的是( B ) A ．a ＝3，b ＝2 B ．a ＝－3，b ＝2 C ．a ＝3，b ＝－1 D ．a ＝－1，b ＝3 9．下列命题是假命题的是( B )A ．锐角小于它的补角B ．内错角相等C ．两点之间线段最短D ．同旁内角互补，两直线平行 10．下列说法正确的是( C )A ．“作线段CD ＝AB”是一个命题B ．过一点作已知直线的平行线有一条且只有一条C ．命题“若x ＝1，则x 2＝1”是真命题D ．命题“若ab>1，则a>b”是真命题11．“直角都相等”的题设是两个角是直角，结论是这两个角相等． 12．对于下列假命题，各举一个反例写在横线上． (1)“如果ac ＝bc ，那么a ＝b”是一个假命题． 反例：3×0＝(－2)×0；(2)“如果a 2＝b 2，则a ＝b”是一个假命题．反例：32＝(－3)2．13．下列命题中：①若|a|＝b ，则a ＝b ；②若直线l 1∥l 2，l 1∥l 3，则l 2∥l 3；③同角的补角相等；④同位角相等，是真命题的有②③(填序号)．14．把下列命题写成“如果……那么……”的形式，并判断其真假． (1)等角的补角相等；(2)不相等的角不是对顶角； (3)相等的角是内错角．解：(1)如果两个角是两个相等的角的补角，那么这两个角相等．是真命题． (2)如果两个角不相等，那么这两个角不是对顶角．是真命题．。
人教版七年级数学下册第五章相交线与平行线：几何计算和证明综合练习试题(含答案)
人教版七年级数学下册第五章相交线与平行线：几何计算和证明综合练习试题1、如图，已知∠2＝∠3，∠C＝∠D，求证：∠A＝∠F.证明：∵∠2＝∠3，∠1＝∠2，∴∠1＝∠3.∴DB∥CE.∴∠DBA＝∠C.∵∠D＝∠C，∴∠D＝∠DBA.∴DF∥AC.∴∠A＝∠F.2、如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．3、如图，∠1＝115°，∠2＝50°，∠3＝65°，EG为∠NEF的平分线．求证：AB∥CD，EG∥FH.证明：∵∠1＝115°，∴∠FCD＝180°－∠1＝180°－115°＝65°.∵∠3＝65°，∴∠FCD＝∠3.∴AB∥CD.∵∠2＝50°，∴∠NEF＝180°－∠2＝180°－50°＝130°.∵EG为∠NEF的平分线，∴∠GEF＝12∠NEF＝65°.∴∠GEF＝∠3.∴EG∥FH.4、如图，已知∠B＝∠D，∠E＝∠F，判断BC与AD的位置关系，并说明理由．解：BC∥AD，理由：∴BE∥FD.∴∠B＝∠BCF.又∵∠B＝∠D，∴∠BCF＝∠D.∴BC∥AD.5、如图，AD⊥BC于点D，EG⊥BC于点G，∠E＝∠1.求证：AD平分∠BAC.证明：∵AD⊥BC，EG⊥BC，∴∠ADC＝∠EGC＝90°.∴AD∥EG.∴∠1＝∠2，∠E＝∠3.∵∠E＝∠1，∴∠2＝∠3.∴AD平分∠BAC.6、如图，B，C，E三点在一条直线上，A，F，E三点在一条直线上，AB∥CD，∠1＝∠2，∠3＝∠4.求证：AD∥BE.证明：∵AB∥CD，∴∠4＝∠BAE.∴∠3＝∠BAE.∵∠1＝∠2，∴∠1＋∠CAF＝∠2＋∠CAF，即∠BAE＝∠CAD.∴∠3＝∠CAD.∴AD∥BE.7、如图，已知AB∥CD，试判断∠B，∠BED和∠D之间的关系，并说明理由．解：∠BED＝∠B＋∠D.理由如下：过点E作EF∥AB，则∠B＝∠BEF.∵AB∥CD，∴EF∥CD.∴∠DEF＝∠D.∵∠BED＝∠BEF＋∠DEF，∴∠BED＝∠B＋∠D.8、如图，∠AEF＋∠CFE＝180°，∠1＝∠2，EG与HF平行吗？为什么？解：平行．理由：∵∠AEF＋∠CFE＝180°，∴AB∥CD.∴∠AEF＝∠EFD.∴∠AEF －∠1＝∠EFD －∠2，即∠GEF ＝∠HFE.∴EG ∥HF.9、如图，A ，B ，C 三点在同一直线上，∠1＝∠2，∠3＝∠D ，试判断BD 与CF 的位置关系，并说明理由．解：BD ∥CF.理由如下：∵∠1＝∠2，∴AD ∥BF.∴∠D ＝∠DBF.∵∠3＝∠D ，∴∠3＝∠DBF.∴BD ∥CF.10、如图，∠ABC ＝∠ADC ，BF ，DE 分别是∠ABC ，∠ADC 的平分线，∠1＝∠2，试说明：DC ∥AB.解：∵BF ，DE 分别是∠ABC ，∠ADC 的平分线，∴∠3＝12∠ADC ，∠2＝12∠ABC. ∵∠ABC ＝∠ADC ，∴∠3＝∠2.∵∠1＝∠2，∴∠1＝∠3.∴DC∥AB.11、如图，AD平分∠BAC，AD⊥BC于D，点E，A，C共线，∠DAC＝∠EFA，延长EF 交BC于点G.求证：EG⊥BC.证明：∵AD平分∠BAC，∴∠DAC＝∠DAB.又∵∠DAC＝∠EFA，∴∠DAB＝∠EFA.∴AD∥EG.∴∠ADC＝∠EGD.∵AD⊥BC，∴∠ADC＝90°.∴∠EGD＝90°.∴EG⊥BC.12、已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB.又∵AB∥CD，∴EF∥AB∥CD.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB.又∵AB∥CD，∴EF∥AB∥CD.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.13、如图，把一张长方形纸片ABCD沿EF折叠后，D，C分别落在D′和C′的位置上，ED′与BC的交点为G.若∠EFG＝50°，求∠1，∠2，∠3的度数．解：根据折叠的性质可知，∠DEF＝∠D′EF，∠EFC＝∠EFC′.∵∠EFG＝50°，∴∠EFC＝180°－50°＝130°.∴∠EFC′＝∠EFC＝130°.∴∠3＝∠EFC′－∠EFG＝130°－50°＝80°.∵AD∥BC，∴∠DEF＝∠EFG＝50°.∴∠DED′＝2∠DEF＝100°.∴∠1＝180°－∠DED′＝180°－100°＝80°.∵AD∥BC，∴∠1＋∠2＝180°.∴∠2＝180°－∠1＝100°.故∠1＝80°，∠2＝100°，∠3＝80°.14、如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3＋60°，∠CBD＝70°.(1)求证：AB∥CD；(2)求∠C的度数．解：(1)证明：∵AE⊥BC，FG⊥BC，∴AE∥GF.∴∠2＝∠A.∵∠1＝∠2，∴∠1＝∠A.∴AB∥CD.(2)∵AB∥CD，∴∠D＋∠CBD＋∠3＝180°.∵∠D ＝∠3＋60°，∠CBD ＝70°，∴∠3＝25°.∵AB ∥CD ，∴∠C ＝∠3＝25°.15、(1)如图1，AB ∥CD ，则∠E ＋∠G 与∠B ＋∠F ＋∠D 有何关系？(2)如图2，若AB ∥CD ，又能得到什么结论？请直接写出结论．解：(1)过点E 作EM ∥AB ，过点F 作FN ∥AB ，过点G 作GH ∥CD. ∵AB ∥CD ，∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1＝∠B ，∠2＝∠3，∠4＝∠5，∠6＝∠D.∴∠1＋∠2＋∠5＋∠6＝∠B ＋∠3＋∠4＋∠D ，即∠BEF ＋∠FGD ＝∠B ＋∠EFG ＋∠D.(2)∠B ＋∠F 1＋∠F 2＋…＋∠F n －1＋∠D ＝∠E 1＋∠E 2＋…＋∠E n .16、已知E ，F 分别是AB ，CD 上的动点，P 也为一动点．(1)如图1，若AB ∥CD ，求证：∠P ＝∠BEP ＋∠PFD ；(2)如图2，若∠P ＝∠PFD －∠BEP ，求证：AB ∥CD ；(3)如图3，AB ∥CD ，移动E ，F ，使∠EPF ＝90°，作∠PEG ＝∠BEP ，则∠AEG∠PFD ＝2．证明：(1)过点P作PG∥AB，则∠EPG＝∠BEP.∵AB∥CD，∴PG∥CD.∴∠GPF＝∠PFD.∴∠EPF＝∠EPG＋∠FPG＝∠BEP＋∠PFD.(2)过点P作PQ∥AB，则∠QPE＝∠BEP.∵∠EPF＝∠PFD－∠BEP，∴∠PFD＝∠EPF＋∠BEP＝∠EPF＋∠QPE＝∠FPQ. ∴DC∥PQ.∴AB∥CD.。
人教版七年级上第五章相交线与平行线综合练习题(含解析)
人教版七年级上第五章相交线与平行线综合练习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列说法错误的是（）A．两个互余的角都是锐角B．锐角的补角大于这个角本身C．互为补角的两个角不可能都是锐角D．锐角大于它的余角2．下列说法中，正确的有（）①两条射线组成的图形叫角；①两点之间，直线最短；①同角（或等角）的余角相等；①连接两点间的线段的长度，叫做这两点的距离．A．1个B．2个C．3个D．4个3．直线AB∥CD，且AD①BC于点E，若①ABE＝32°，则①ADC的度数为（）A．68°B．58°C．48°D．68°⊥，OG平分①EOF，若4．如图，直线AB，CD交于点O，OE平分①AOC，OF AB∠=，则①AOG等于（）48BOCA．10B．12︒C．14D．165．下列说法中，正确的是（）A．一条射线把一个角分成两个角，这条射线叫做这个角的平分线B．P是直线l外一点，A，B，C分别是l上的三点，已知P A=1，PB=2，PC=3，则点P 到直线l的距离一定是1C．相等的角是对顶角D．钝角的补角一定是锐角6．如图所示，下列说法错误的是（）A．①1和①3是同位角B．①1和①5是同位角C．①1和①2是同旁内角D．①5和①6是内错角7．如图，在①ABC中，点D、E分别是AB、AC的中点，若①B=40°，则①BDE的度数为（）A．40°B．50°C．140°D．150°8．如图，已知点B、D、C、F在同一条直线上，AB EF，AB＝EF，AC DE，如果BF＝6，DC＝3，那么BD的长等于（）A．1B．32C．2D．39．下列语句中，是命题的是（）A．两个相等的角是对顶角B．在直线AB上任取一点C C．用量角器量角的度数D．直角都相等吗？10．下列汽车标志中可以看作是由某图案平移得到的是（）A．B．C．D．二、填空题11．如图，直线AB和CD交于O点，OD平分①BOF，OE ①CD于点O，①AOC=40︒，则①EOF=_______．12．如图，直线a①b，直线c与直线a，b相交，若①1＝54°，则①3＝________度．13．如图，将一副直角三角尺的直角顶点C 叠放在一起，若CE、CD分别平分①ACD 与①ECB，则计算①ECD=___________度．14．如图，将△ABC纸片沿DE折叠，使C落在点C'处，且BC'平分①ABC，AC'平分①BAC的外角，若①1＝68°，①2＝112°，则①BC A'＝______15．如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西________度．16．如图，把长方形ABCD 沿EF 对折后使两部分重合，若160∠=︒，则∠=AEF _______．17．下列说法中：（1）不相交的两条直线叫做平行线；（2）经过一点，有且只有一条直线与已知直线平行；（3）垂直于同一条直线的两直线平行；（4）直线//a b ，//b c ，则//a c ；（5）两条直线被第三条直线所截，同位角相等．其中正确的是________．18．命题“正数的平方根的和为零”，写成“如果……，那么……”是____．19．如图，在一块长为a 米、宽为b 米的长方形地上，有一条弯曲的柏油马路，马路的任何地方的水平宽度都是2米，其他部分都是草地，则草地的面积为__________平方米．20．将直角梯形ABCD 平移得梯形EFGH ，若10,2,4HG MC MG ===，则图中阴影部分的面积为_________平方单位．三、解答题21．如图，已知①D＝①B，DF①AC，BE①AC．(1)求证：AD①BC；(2)若AE＝CF，求证：①AFD①①CEB．22．请完成下面的推理过程：如图，已知①D＝108°，①BAD＝72°，AC①BC于C，EF①BC于F．求证：①1＝①2．证明：①①D＝108°，①BAD＝72°（已知）①①D+①BAD＝180°AB CD（）①//①①1＝（）又①AC①BC于C，EF①BC于F（已知）①EF//（）①①2＝（）①①1＝①2（）23．(1)【自主学习】填空：如图1，点C 是MON ∠的平分线OP 上一点，点A 在OM 上，用圆规在ON 上截取OB OA =，连接BC ，可得OAC ∆≅ ，其理由根据是 ；(2)【理解运用】如图2，在Rt ABC ∆中，90ACB ∠=︒，60A ∠=︒，CD 平分ACB ∠，试判断BC 和AC 、AD 之间的数量关系并写出证明过程．(3)【拓展延伸】如图3，在ABC ∆中，60A ∠=︒，CD ，BE 分别是ACB ∠，ABC ∠的平分线，CD ，BE 交于点F ，若3CE =，2BD =，请直接写出BC 的长．24．将正方形的四个顶点用线段连接，什么样的连法最短？研究发现，并非对角线最短，而是如图的连法最短（即用线段AE ，DE ，EF ，BF ，CF 把四个顶点连接起来）已知图中30DAE ADE ∠=∠=︒，120AEF BFE ∠=∠=︒，你能证明此时AB EF ∥吗？25．已知：如图，在ABC 中，60A ∠=︒，70C ∠=︒，点D ，E 分别在AB 和AC 上，且DE BC ∥．求证：50ADE ∠=︒．参考答案：1．D【分析】根据补角、余角的定义逐个判断即可得出结论．【详解】解：A、两角互余，和为90°，两角均为锐角，故A不符合题意B、两角互补，和为180°，从而锐角的补角必为钝角，故B不符合题意C、两角互补，和为180°，两锐角的和必小于180°，故C不符合题意D、两角互余，和为90°，从而锐角不一定大于它的余角，也可以小于或者等于它的余角，故D不符合题意故选：D．【点睛】本题主要考查了互为补角、互为余角的定义，解题的关键是熟练掌握互为补角、互为余角的定义．2．B【分析】由角的概念判断①，由线段的性质判断①，由补角与余角的性质判断①，由两点间的距离概念判断①，从而可得答案．【详解】解：有公共端点的两条射线组成的图形叫角，故①说法错误，不符合题意，两点之间，线段最短，故①说法错误，不符合题意；同角（或等角）的余角相等，故①说法正确，符合题意；连接两点间的线段的长度，叫做这两点的距离，故①说法正确，符合题意；故选：.B【点睛】本题考查的是角的概念，线段的性质，补角与余角的性质，两点间的距离，掌握以上知识是解题的关键．3．B【分析】根据AB∥CD，可得①ABE=①BCD，再由直角三角形两锐角互余，可求出答案．【详解】解：①AB∥CD，且①ABE＝32°，①①ABE=①BCD=32°；①AD①BC于点E，①①CED=90°，①①ECD＋①EDC=90°，①①ADC=58°，故选：B．【点睛】本题考查平行线的性质，垂直的定义，熟练运用性质转化角度关系是解题的关键．4．B【分析】分别求出①AOE和①EOG，然后根据①AOG＝①EOG﹣①AOE计算即可得解．【详解】解：①①BOC＝48°，①①AOC＝180°﹣48°＝132°，①OE平分①AOC，①①AOE＝①EOC＝12①AOC＝1132662⨯︒=︒，①OF①AB，①①BOF＝90°，①①EOF＝360°﹣①EOC﹣①BOC﹣①BOF ＝360°﹣66°﹣48°﹣90°＝156°①OG平分①EOF，①①EOG＝①FOG＝12EOF∠＝11562⨯︒＝78°，①①AOG＝①EOG﹣①AOE＝78°﹣66°＝12°，故选：B．【点睛】本题考查了角的计算，主要利用了角平分线的定义，熟记概念并准确识图，理清图中各个角度之间的关系是解题的关键．5．D【分析】分别根据角平分线的定义，点到直线的距离，对顶角定义，钝角、锐角及补角的概念逐项判断即可．【详解】A.分成的两个角不一定相等，不符合题意；B.P A不一定与l垂直，不符合题意；C.相等的两个角不一定是对顶角，不符合题意；D.钝角的补角一定是锐角，符合题意．故选D．【点睛】本题考查了角平分线的定义，点到直线的距离，对顶角定义，钝角、锐角及补角的概念，熟悉概念是解题的关键．6．B【分析】根据同位角、内错角、同旁内角的意义：两条直线被第三条直线所截，在截线的同旁，在被截的两直线的同一侧的角叫做同位角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间的两个角叫做内错角；两条直线被第三条直线所截，在截线同旁，且在被截两条直线之内的两角叫做同旁内角，可得答案．【详解】解：A、①1和①3是同位角，故此选项不符合题意；B、①1和①5不存在直接联系，故此选项符合题意；C、①1和①2是同旁内角，故此选项不符合题意；D、①1和①6是内错角，故此选项不符合题意；故选B．【点睛】本题考查了同位角、内错角、用旁内角，利用同位角、内错角、同旁内角的意义是解题关键．7．C【分析】由条件可知DE是①ABC的中位线，即DE①BC，根据平行线的性质即可求出①BDE 的度数为140°．【详解】解：①点D、E分别是AB、AC的中点，①DE是①ABC的中位线，①DE∥BC，即：①B+①BDE=180°，①①BDE=180°-①B=180°-40°=140°．故选：C．【点睛】本题主要考查的是三角形中位线的性质，以及平行线的性质的应用，掌握中位线的性质是解题的关键．8．B【分析】由AB EF得①B＝①F，由AC DE得①ACB＝①EDF，从而证明①ABC①①EFD得BC＝FD，即可求得BD的长．【详解】解：①AB EF，①①B＝①F，①AC DE，①①ACB＝①EDF，在①ABC和①EFD中，ACB EDF B FAB EF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ①①ABC ①①EFD （AAS ），①BC ＝FD ，①BC ﹣DC ＝FD ﹣DC ，①BD ＝FC ，①BD ＝12（BF ﹣DC ）＝12（6﹣3）＝32． 故选：B ．【点睛】本题主要考查了平行线的性质、三角形全的的判定及性质，熟练掌握三角形全的的判定方法是解题的关键．9．A【分析】根据命题的定义逐一判断即可．【详解】解：A ．“两个相等的角是对顶角”做出了判断，是命题；B ．“在直线AB 上任取一点C ”没有做出判断，不是命题；C ．“用量角器量角的度数”没有做出判断，不是命题；D ．“直角都相等吗？”没有做出判断，不是命题；故选：A ．【点睛】此题主要考查了命题的含义和应用，解答此题的关键是要明确：判断一件事情的语句叫命题，许多命题都是由题设和结论两部分组成．10．D【分析】根据平移不改变图形的形状和大小，结合图案，对选项一一分析，排除错误答案．【详解】解：A 、是一个旋转对称图形，不能由平移得到，故此选项不合题意；B 、是一个对称图形，不能由平移得到，故此选项不合题意；C 、是一个旋转对称图形，不能由平移得到，故此选项不合题意；D 、图案自身的一部分沿着直线运动而得到，是平移，故此选项符合题意．故选：D ．【点睛】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，注意分清图形的平移与旋转或翻转．11．130°【分析】根据对顶角性质可得①BOD =①AOC=40°．根据OD 平分①BOF ，可得①DOF =①BOD =40°，根据OE ①CD ，得出①EOD =90°，利用两角和得出①EOF =①EOD +①DOF =130°即可．【详解】解：①AB 、CD 相交于点O ，①①BOD =①AOC=40°．①OD 平分①BOF ，①①DOF =①BOD =40°，①OE ①CD ，①①EOD =90°，①①EOF =①EOD +①DOF =130°．故答案为130°．【点睛】本题考查相交线对顶角性质，角平分线定义，垂直定义，掌握对顶角性质，角平分线定义，垂直定义是解题关键．12．54【分析】根据对顶角相等和平行线的性质“两直线平行同位角相等”，通过等量代换求解．【详解】因为a①b ，所以23∠=∠，因为12∠∠，是对顶角， 所以12∠=∠，所以31∠=∠，因为154∠=︒，所以354∠=︒，故答案为：54．【点睛】本题考查了平行线的性质和对顶角的性质，熟练掌握对顶角相等，两直线平行同位角相等、内错角相等，加以灵活运用求解相关角的度数是解题关键．13．45【分析】由题意可知90ACD ∠=︒，根据角平分线的性质即可求解．【详解】解：由题意可知90ACD ∠=︒，又①CE 平分ACD ∠ ①1=452ECD ACD ∠=∠︒ 故答案为45【点睛】此题考查了角平分线的性质，熟练掌握角平分线的有关性质是解题的关键． 14．11°##11度【分析】连接CC '，先根据三角形外角的性质和折叠的性质可得①ACB ＝22°，由角平分线的定义和三角形外角的性质可得结论．【详解】解：如图，连接CC '，由折叠得：CE ＝C E '，DC ＝DC '，①DCE ＝①DC E '，①ECC EC C ''∠=∠，DCC DC C ''∠=∠，①①1＝DCC DC C ''∠+∠＝68°，①2＝ECC EC C ''∠+∠＝112°，①DCC '∠＝34°，ECC '∠＝56°，①①ACB ＝56°﹣34°＝22°，①BC '平分①ABC ，AC '平分①BAC 的外角，①①FAC '12=①F AC ，①ABC '12=①ABC ， ①①BC A '＝①FAC '﹣①ABC '12=①F AC 12-①ABC 12=①ACB ＝11°． 故答案为：11°．【点睛】本题主要考查角平分线的定义、图形折叠的性质、三角形外角的性质，熟练掌握相关性质是解决本题的关键．15．48°【详解】先根据题意画出图形，利用平行线的性质解答即可．解：如图，①AC①BD ，①1=48°，①①2=①1=48°，根据方向角的概念可知，乙地所修公路的走向是南偏西48°．16．120︒【分析】如图，先求解120,BFB '∠=︒再利用轴对称的含义求解,BFE ∠ 再利用平行线的性质可得答案. 【详解】解：如图， 160∠=︒，则18060120,BFB '∠=︒-︒=︒由对折可得：160,2BFE BFB '∠=∠=︒ 长方形ABCD ,//,AD BC ∴=180120,AEF BFE ∴∠︒-∠=︒故答案为：120.︒【点睛】本题考查的是长方形的性质，邻补角的定义，轴对称的含义，平行线的性质，掌握以上知识是解题的关键.17．（4）【分析】根据平行线的定义，平行线的性质，平行公理的推论解答．【详解】（1）在同一平面内不相交的两条直线叫做平行线，故该项错误；（2）过直线外一点，有且只有一条直线与已知直线平行，故该项错误；（3）在同一平面内，垂直于同一条直线的两直线平行，故该项错误；（4）直线//a b ，//b c ，则//a c ，故该项正确；（5）两条平行线被第三条直线所截，同位角相等，故该项错误．故选：（4）．【点睛】此题考查判断语句，熟记平行线的定义，平行线的性质，平行公理的推论是解题的关键．18．如果一个数为正数，那么它的平方根的和为0．【分析】根据命题都可以写成“如果”、“那么”的形式，“如果”后面是题设，“那么”后面是结论，从而得出答案．【详解】如果一个数为正数，那么它的平方根的和为0．故答案为如果一个数为正数，那么它的平方根的和为0．【点睛】此题考查了命题与定理，解题的关键是了解“如果”后面是题设，“那么”后面是结论． 19．（ab ﹣2b ）【分析】根据图形的特点，可以把小路的面积看作是一个底是2米，高是b 米的平行四边形，根据平行四边形的面积＝底×高，长方形的面积＝长×宽，用长方形的面积减去小路的面积即可．【详解】解：由题可得，草地的面积是(ab ﹣2b )平方米．故答案为：(ab ﹣2b )．【点睛】本题考查了平移的实际应用．化曲为直是解题的关键．20．36【分析】根据图形可知图中阴影部分的面积等于梯形ABCD 的面积减去梯形EFMD 的面积，恰好等于梯形EFGH 的面积减去梯形EFMD 的面积．【详解】根据平移的性质得S 梯形ABCD =S 梯形EFGH ，DC = HG = 10，MC = 2，MG = 4，∴DM = DC - MC = 10 - 2 = 8，∴S 阴影= S 梯形ABCD -S 梯形EFMD=S 梯形EFGH -S 梯形EFMD=S 梯形HGMD =()12DM HG MG + =12×(8+10)×4= 36．故答案为：36．【点睛】主要考查了梯形的性质和平移的性质，要注意平移前后图形的形状和大小不变，本题的关键是能得到：图中阴影部分的面积等于梯形ABCD 的面积减去梯形EFMD 的面积，恰好等于梯形EFGH 的面积减去梯形EFMD 的面积．21．(1)见解析(2)见解析【分析】（1）证明①A ＝①C ，根据内错角相等，两直线平行即可进行证明；（2）根据AAS 即可证明①AFD ①①CEB ．（1）证明：①DF ①AC ，BE ①AC ．①①AFD ＝90°，①BEC ＝90°，①①D ＝①B ，①①A ＝①C ，①AD BC ∥；（2）①AE ＝CF ，①AE ﹣EF ＝CF ﹣EF ，①AF ＝CE ，在①AFD 和①CEB 中，D B A C AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，①①AFD ①①CEB （AAS ）．【点睛】本题主要考查了平行线的判定和三角形全等的判定，熟练掌握平行线的性质和三角形的判定定理是解题的关键．22．见解析【分析】由直线相交及平行的相关定理性质即可得到答案．【详解】解：①①D ＝108°，①BAD ＝72°（已知）①①D +①BAD ＝180°①//AB CD （ 同旁内角互补，两直线平行）①①1＝3∠（两直线平行，内错角相等）又①AC ①BC 于C ，EF ①BC 于F （已知）①EF //AC （垂直于同一直线的两条直线平行）①①2＝3∠（两直线平行，同位角相等）①①1＝①2（等量代换）【点睛】本题考查直线相交及平行的相关定理性质，熟练掌握相关知识是解题的关键． 23．(1)OBC ∆，SAS(2)BC AC AD =+，证明见解析(3)5【分析】（1）由角平分线的定义得出AOC BOC ∠=∠，根据SAS 可证明OAC OBC ∆≅∆； （2）先截取CE CA =，连接DE ，根据SAS 判定CAD CED ∆≅∆，得出AD DE =，60A CED ∠=∠=︒，AC CE =，进而得出结论BC AC AD =+；（3）在BC 上取一点M ，使CM CE =，证明()CEF CMF SAS ∆≅∆，由全等三角形的性质得出60CFE CFM ∠=∠=︒，证明()FBM FBD ASA ∆≅∆，由全等三角形的性质得出BM BD =，则可求出答案．（1） 解：点C 是MON ∠的平分线OP 上一点，AOC BOC ∠=∠∴，在OAC ∆和OBC ∆中，OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩，()OAC OBC SAS ∴∆≅∆，故答案为：OBC ∆；SAS ；（2）BC AC AD =+．证明：在CB 上截取CE CA =，CD 平分ACB ∠，ACD BCD ∴∠=∠，在ACD ∆和ECD ∆中，AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩，()ACD ECD SAS ∴∆≅∆，60CAD CED ∴∠=∠=︒，AD=DE ，90ACB ∠=︒，30B ∴∠=︒，30EDB ∴∠=︒，即EDB B ∠=∠，DE EB ∴=，BC CE BE =+，BC AC DE ∴=+，BC AC AD ∴=+．（3）在BC 上取一点M ，使CM CE =，在ABC ∆中，180A ABC ACB ∠+∠+∠=︒，60A ∠=︒，180120ABC ACB A ∴∠+∠=︒-∠=︒，1180()180()1202BFC BCF CBF ACB ABC ∴∠=︒-∠+∠=︒-∠+∠=︒， 60CFE ∴∠=︒，60BFD CFE ∴∠=∠=︒， CD 平分ACB ∠，ECF MCF ∴∠=∠，在CEF ∆和CMF ∆中，CE CM ECF MCF CF CF =⎧⎪∠=∠⎨⎪=⎩，()CEF CMF SAS ∴∆≅∆，60CFE CFM ∴∠=∠=︒，60BFM BFC CFM ∴∠=∠-∠=︒，60BFM BFD ∴∠=∠=︒， BE 是ACB ∠的平分线，FBM FBD ∴∠=∠，在FBM ∆和FBD ∆中，BFM BFD BF BF FBM FBD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()FBM FBD ASA ∴∆≅∆，BM BD ∴=，325BC CM BM CE BD ∴=+=+=+=．【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质，等边三角形的判定与性质，角平分线的性质以及等腰三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，根据线段的和差关系进行推导．24．见解析【分析】根据正方形的性质可得90DAB ∠=︒，结合已知条件可得60EAB ∠=︒， 由已知条件120AEF ∠=︒，进而根据同旁内角互补，两直线平行，即可证明AB EF ∥． 【详解】证明：四边形ABCD 是正方形，∴90DAB ∠=︒，30DAE ∠=︒，903060BAE ∴∠=︒-︒=︒，120AEF ∠=︒，180AEF BAE ∴∠+∠=︒，∴AB EF ∥．【点睛】本题考查了平行线的判定，掌握同旁内角互补，两直线平行是解题的关键． 25．见解析【分析】根据三角形内角和定理求得50B ∠=︒，根据平行线的性质求得ADE B ∠=∠，进而即可证明50ADE ∠=︒．【详解】在ABC 中，①60A ∠=︒，70C ∠=︒ （已知），①18050B A C ∠=︒-∠-∠=︒（三角形内角和定理）．又①DE BC ∥（已知），①ADE B ∠=∠（两直线平行，同位角相等）．①50ADE ∠=︒（等量代换）．【点睛】本题考查了三角形内角和定理，平行线的性质，掌握平行线的性质是解题的关键．。
人教版数学七年级下册：第五章 相交线与平行线——专题练习(附答案)
小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝度．小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( )A．20° B．25° C．30° D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝．∵DF∥CA，∴∠A＝．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD( )，∴∠C＝．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝ (垂直的定义)．②所以 (同位角相等，两直线平行)．③所以∠1＋∠2＝ (两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°( )，⑤所以∠1＝∠3( )．⑥所以AB∥DG( )．⑦所以∠GDC＝∠B( )．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．参考答案：小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．【解答】∠BED＝∠B＋∠D.理由：过点E作EF∥AB，则EF∥CD.∴∠B＝∠BEF，∠D＝∠DEF.∴∠BED＝∠BEF＋∠DEF＝∠B＋∠D.变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.拓展平行线间有多个拐点2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？解：(1)∠BEF＋∠FGD＝∠B＋∠EFG＋∠D.理由：过点E，F，G分别作EM∥AB，FN∥AB，GH∥AB，由AB∥CD，得AB∥EM∥FN∥GH∥CD.∴∠BEM＝∠B，∠MEF＝∠EFN，∠NFG＝∠FGH，∠HGD＝∠D.∴∠BEF＋∠FGD＝∠BEM＋∠MEF＋∠FGH＋∠HGD＝∠B＋∠EFN＋∠NFG＋∠D＝∠B＋∠EFG＋∠D.(2)在图2中，有∠E1＋∠E2＋∠E3＋…＋∠En＝∠B＋∠F1＋∠F2＋…＋∠Fn－1＋∠D.如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？【解答】∠B＋∠BED＋∠D＝360°.理由：过点E作EF∥AB.∵AB∥CD，∴AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠D＋∠DEF＝180°. ∴∠B＋∠BEF＋∠D＋∠DEF＝360°，即∠B＋∠BED＋∠D＝360°.拓展平行线间有多个拐点3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝180度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝360度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝540度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝720度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝180(n－1)度．解：每增加一个角，度数增加180°.小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( C ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( D )A．20° B．25° C．30°D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝130°．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．∵∠BAC＝80°，∴∠AGD＝100°.类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( D )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( B )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝128°．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是65°．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是76度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是90°．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝∠BFD(两直线平行，内错角相等)．∵DF∥CA，∴∠A＝∠BFD(两直线平行，同位角相等)．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD(对顶角相等)，∴∠C＝∠D．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝90°(垂直的定义)．②所以AD∥EF(同位角相等，两直线平行)．③所以∠1＋∠2＝180°(两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°(已知)，⑤所以∠1＝∠3(同角的补角相等)．⑥所以AB∥DG(内错角相等，两直线平行)．⑦所以∠GDC＝∠B(两直线平行，同位角相等)．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.证明：∵DF∥AB(已知)，∴∠D＝∠BHM(两直线平行，同位角相等)．又∵∠B＝75°，∠D＝105°(已知)，∴∠B＋∠BHM＝75°＋105°＝180°.∴DE∥BC(同旁内角互补，两直线平行)．∴∠AME＝∠AGC(两直线平行，同位角相等)．3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.证明：∵AE平分∠BAD(已知)，∴∠1＝∠2(角平分线的定义)．∵AB∥CD(已知)，∴∠1＝∠CFE(两直线平行，同位角相等)．又∵∠1＝∠2(已证)，∠CFE＝∠E(已知)，∴∠2＝∠E(等量代换)．∴AD∥BC(内错角相等，两直线平行)．4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．解：DF∥AB.理由：∵BE是∠ABC的平分线，∴∠1＝∠2(角平分线的定义)．∵∠E＝∠1(已知)，∴∠E＝∠2(等量代换)．∴AE∥BC(内错角相等，两直线平行)．∴∠A＋∠ABC＝180°(两直线平行，同旁内角互补)．∵∠3＋∠ABC＝180°(已知)，∴∠A＝∠3(等量代换)．∴DF∥AB(同位角相等，两直线平行)．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.证明：∵AE平分∠BAC，CE平分∠ACD(已知)，∴∠BAC＝2∠1，∠ACD＝2∠2(角平分线的性质)．∴∠BAC＋∠ACD＝2∠1＋2∠2＝2(∠1＋∠2)．∵∠1＋∠2＝90°(已知)，∴∠BAC＋∠ACD＝180°.∴AB∥CD(同旁内角互补，两直线平行)．∴∠B＋∠D＝180°(两直线平行，同旁内角互补)．∴∠D＝180°－∠B(等式的性质)．∵AB⊥BD(已知)，∴∠B＝90°(垂直的定义)．∴∠D＝90°，即CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．解：∵AD∥BC，∠EFG＝55°，∴∠2＝∠GED，∠DEF＝∠EFG＝55°(两直线平行，内错角相等)．由折叠，知∠GEF＝∠DEF＝55°.∴∠GED＝110°.∴∠2＝110°.∴∠1＝180°－∠2＝70°(两直线平行，同旁内角互补)．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．解：(1)证明：∵BC∥GE，∴∠E＝∠1＝50°.∵∠AFG＝∠1＝50°，∴∠E＝∠AFG＝50°.∴AF∥DE.(2)过点A作AP∥GE，∵BC∥GE，∴AP∥GE∥BC.∴∠FAP＝∠AFG＝50°，∠PAQ＝∠Q＝15°.∴∠FAQ＝∠FAP＋∠PAQ＝65°.∵AQ平分∠FAC，∴∠CAQ＝∠FAQ＝65°.∴∠CAP＝80°.∴∠ACQ＝180°－∠CAP＝100°.。
2024-2025学年人教版数学七年级下学期《第5章相交线与平行线》测试卷及答案解析
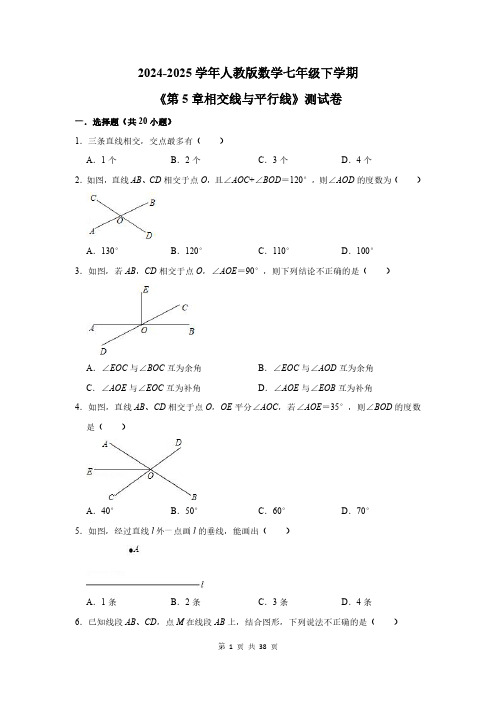
A．3.5
B．4
10．如图，下列说法错误的是（ ）
C．5.5
第 2 页 共 38 页
D．6.5
A．∠A 与∠B 是同旁内角
B．∠1 与∠3 是同位角
C．∠2 与∠A 是同位角
D．∠2 与∠3 是内错角
11．下列所示的四个图形中，∠1 和∠2 是同位角的是（ ）
A．①②
B．②③
12．如图，∠BAC 和∠BCA 是（ ）
A．A 点
B．B 点
C．C 点
8．下列图形中，线段 MN 的长度表示点 M 到直线 l 的距离的是（
D．D 点 ）
A．
B．
C．
D．
9．如图，A 是直线 l 外一点，过点 A 作 AB⊥l 于点 B，在直线 l 上取一点 C，连结 AC，使
AC＝2ABLeabharlann P 在线段 BC 上连结 AP．若 AB＝3，则线段 AP 的长不可能是（ ）
循反射定律发生反射，当光线 PQ 经过 n 次反射后与边 OA 或 OB 平行时，称角为定角α
的 n 阶平行逃逸角，特别地，当光线 PQ 直接与 OA 平行时，称角β为定角α的零阶平行
逃逸角．
（1）已知∠AOB＝α＝20°，
①如图 1，若 PQ∥OA，则∠BPQ＝
°，即该角为α的零阶平行逃逸角；
第 5 页 共 38 页
25．已知，如图，∠1＝∠ABC＝∠ADC，∠3＝∠5，∠2＝∠4，∠ABC+∠BCD＝180°，
C．110°
D．100°
3．如图，若 AB，CD 相交于点 O，∠AOE＝90°，则下列结论不正确的是（ ）
A．∠EOC 与∠BOC 互为余角
B．∠EOC 与∠AOD 互为余角
最新人教版七年级数学下册第五章相交线与平行线专项测试试卷(含答案详细解析)
七年级数学下册第五章相交线与平行线专项测试（2021-2022学年考试时间：90分钟，总分100分）班级：__________ 姓名：__________ 总分：__________一、单选题（10小题，每小题3分，共计30分）1、下列命题：①平面内，垂直于同一条直线的两直线平行；②经过直线外一点，有且只有一条直线与这条直线平行；③垂线段最短；④同旁内角互补．其中，正确命题的个数有（）A．1个B．2个C．3个D．4个2、如图，O为直线AB上一点，∠COB＝36°12'，则∠AOC的度数为（）A．164°12'B．136°12'C．143°88'D．143°48'3、下列各组图形中，能够通过平移得到的一组是（）A． B． C． D．4、如图，直线AB∥CD，直线AB、CD被直线EF所截，交点分别为点M、点N，若∠AME＝130°，则∠DNM的度数为（）A．30°B．40°C．50°D．60°5、“小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是（）A．平移变换B．翻折变换C．旋转变换D．以上都不对6、如图，下列条件中，不能判断1l∥2l的是（）A．∠1=∠3B．∠2=∠4C．∠4+∠5=180°D．∠3=∠47、下列各图中，∠1与∠2是对顶角的是（）A．B．C．D．8、如所示各图中，∠1与∠2是对顶角的是（ ）A ．B ．C ．D ．9、下列命题中，真命题是（ ）A ．两条直线被第三条直线所截，内错角相等B ．相等的角是对顶角C ．在同一平面内，垂直于同一条直线的两条直线平行D ．同旁内角互补10、在证明命题“若21a >，则1a >”是假命题时，下列选项中所举反例不正确的是（ ）A ．2a =B ．2a =-C ．3a =-D ．4a =-二、填空题（5小题，每小题4分，共计20分）1、如图，过直线AB 上一点O 作射线OC ，∠BOC ＝29°38′，OD 平分∠AOC ，则∠DOC 的度数为 _____．2、如图，（1）∠1和∠ABC是直线AB、CE被直线________所截得的________角；（2）∠2和∠BAC是直线CE、AB被直线________所截得的________角；（3）∠3和∠ABC是直线________、________被直线________所截得的________角；（4）∠ABC和∠ACD是直线________、________被直线_________所截得的________角；（5）∠ABC和∠BCE是直线________、________被直线________所截得的________角．3、如图，已知1234l l l l，且∠1=48°，则∠2＝_____，∠3＝_____，∠4＝_____．//,//4、如图，线段AB按一定的方向平移到线段CD，点A平移到点C，若AB=6cm，四边形ABDC的周长为28cm，则BD=_____cm．5、如图，A、B、C为直线l上的点，D为直线l外一点，若2∠的度数为＝，则CBD∠∠ABD CBD______．三、解答题（5小题，每小题10分，共计50分）1、在如图所示的方格纸中，每个小正方形的顶点称为格点，每个小正方形的边长为1，已知四边形ABCD的四个顶点在格点上，利用格点和直尺按下列要求画图：（1）过点C画AD的平行线CE；（2）过点B 画CD 的垂线，垂足为F ．2、如图所示，已知∠AOD =∠BOC ，请在图中找出∠BOC 的补角，邻补角及对顶角．3、如图，直线,AB CD 交于点O ，OE CD ⊥于点O ，且BOD ∠的度数是AOD ∠的4倍．（1）求AOD BOD ∠∠,的度数；（2）求∠BOE 的度数．4、完成下列证明：已知CD AB ⊥，FG AB ⊥，垂足分别为D 、F ，且12∠=∠，求证∥DE BC ． 证明：AB CD ⊥，FG AB ⊥（已知），90BDC BFG ∴∠=∠=︒（ ）CD GF ∴∥（ ）23∴∠=∠（ ）又12∠=∠（已知）13∠∠∴=（ ）DE BC ∴∥（ ）5、按下面的要求画图，并回答问题：（1）如图①，点M 从点O 出发向正东方向移动4个格，再向正北方向移动3个格．画出线段OM ，此时M 点在点O 的北偏东 °方向上（精确到1°），O 、M 两点的距离是 cm ．（2）根据以下语句，在“图②”上边的空白处画出图形．画4cm 长的线段AB ，点P 是直纸AB 外一点，过点P 画直线AB 的垂线PD ，垂足为点D ．你测得点P 到AB 的距离是 cm ．---------参考答案-----------一、单选题【分析】根据平行线的性质与判定可以判断①②④，根据垂线段最短可以判断③．【详解】解：①平面内，垂直于同一条直线的两直线平行，是真命题；②经过直线外一点，有且只有一条直线与这条直线平行，是真命题；③垂线段最短，是真命题；④两直线平行，同旁内角互补，是假命题，∴真命题有3个，故选C．【点睛】本题主要考查了判断命题真假，熟知相关知识是解题的关键．2、D【分析】根据邻补角及角度的运算可直接进行求解．【详解】解：由图可知：∠AOC+∠BOC=180°，∵∠COB＝36°12'，∴∠AOC=180°-∠BOC=143°48'，故选D．【点睛】本题主要考查邻补角及角度的运算，熟练掌握邻补角及角度的运算是解题的关键．【分析】根据平移的性质对各选项进行判断．【详解】A、左图是通过翻折得到右图，不是平移，故不符合题意；B、上图可通过平移得到下图，故符合题意；C、不能通过平移得到，故不符合题意；D、不能通过平移得到，故不符合题意；故选B．【点睛】本题主要考查平移的性质，熟练掌握平移的性质是解题的关键．4、C【分析】由对顶角得到∠BMN=130°，然后利用平行线的性质，即可得到答案．【详解】解：由题意，∵∠BMN与∠AME是对顶角，∴∠BMN=∠AME=130°，∵AB∥CD，∴∠BMN+∠DNM=180°，∴∠DNM=50°；故选：C．【点睛】本题考查了平行线的性质，对顶角相等，解题的关键是掌握所学的知识，正确得到∠BMN =130°．5、A【分析】根据平移是图形沿某一直线方向移动一定的距离，可得答案．【详解】解：“小小竹排水中游，巍巍青山两岸走”所描绘的图形变换主要是平移变换，故选：A ．【点睛】本题考查了平移变换，利用了平移的定义．6、D【分析】根据平行线的判定定理对各选项进行逐一判断即可．【详解】解：A 、13∠=∠，内错角相等，12//l l ∴，故本选项错误，不符合题意；B 、24∠∠=，同位角相等，12//l l ∴，故本选项错误，不符合题意；C 、45180∠+∠=︒，同旁内角互补，12//l l ∴，故本选项错误，不符合题意；D 、34∠∠=，它们不是内错角或同位角，1l 与2l 的关系无法判定，故本选项正确，符合题意．故选：D ．【点睛】本题考查的是平行线的判定，解题的关键是熟知同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行的知识．7、B【分析】根据对顶角的定义作出判断即可．【详解】解：根据对顶角的定义可知：只有B 选项的是对顶角，其它都不是．故选：B ．【点睛】本题考查对顶角的定义，解题关键是明确两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．8、B【分析】根据对顶角的定义进行判断：两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做对顶角．【详解】解：A ．∠1与∠2没有公共顶点，不是对顶角；B ．∠1与∠2有公共顶点，并且两边互为反向延长线，是对顶角；C ．∠1与∠2虽然有公共顶点，但两个角的两边不互为反向延长线，不是对顶角；D ．∠1与∠2虽然有公共顶点，但两个角的两边不互为反向延长线，不是对顶角．故选：B．【点睛】本题主要考查了对顶角的定义，熟记对顶角的定义是解题的关键．9、C【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．【详解】解：A、错误，当被截的直线平行时形成的同位角才相等；B、错误，对顶角相等但相等的角不一定是对顶角；C、正确，必须强调在同一平面内；D、错误，两直线平行同旁内角才互补．故选：C．【点睛】主要考查命题的真假判断与平行线的性质、对顶角的特点，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．10、A【分析】所谓举反例是指满足命题的条件但不满足命题的结论，由此可判断．【详解】显然A选项既满足命题的条件也满足命题的结论，故不是举反例，其它三个选项满足命题的条件，但不满足命题的结论，所以都是举反例；故选：A【点睛】本题考查了命题的真假，说明一个命题是假命题要举反例．掌握举反例的含义是关键．二、填空题1、7511'︒【解析】【分析】先根据邻补角互补求出∠AOC=150°22′，再由角平分线的定义求解即可．【详解】解：∵∠BOC＝29°38′，∠AOC+∠BOC=180°，∴∠AOC=150°22′，∵OD平分∠AOC，∴1=75112DOC AOC'=︒∠∠，故答案为：7511'︒．【点睛】本题主要考查了邻补角互补，角度制的计算，角平分线的定义，熟知相关知识是解题的关键．2、BD（BC）同位AC内错AB AC BC同旁内AB AC BC同位AB CE BC同旁内【解析】【分析】根据同位角、内错角、同旁内角的性质判断即可；【详解】（1）∠1和∠ABC是直线AB、CE被直线BD（BC）所截得的同位角；（2）∠2和∠BAC是直线CE、AB被直线AC所截得的内错角；（3）∠3和∠ABC是直线AB、AC被直线BC所截得的同旁内角；（4）∠ABC和∠ACD是直线AB、AC被直线BC所截得的同位角；（5）∠ABC和∠BCE是直线AB、CE被直线BC所截得的同旁内角．故答案是：BD（BC）；同位；AC；内错；AB；AC；BC；同旁内；AB；AC；BC；同位；AB；CE；BC；同旁内．【点睛】本题主要考查了同位角、内错角、同旁内角的判断，准确分析判断是解题的关键．3、48° 132° 48°【解析】【分析】根据两直线平行内错角相等可求出∠2，根据两直线平行，同位角相等可求出∠4，同旁内角互补可求出∠3．【详解】解：∵1l //2l，∠1=48°，∴∠2=∠1=48°，∵3l //4l，∠1=48°，∴∠4=∠1=48°，∵1l //2l，∴∠3+∠4=180°∴∠3=180°-∠4=180°-48°=132°故答案为：48°；132°；48°【点睛】此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．4、8【解析】【分析】图形平移后，AB平移到线段CD，点A平移到点C，则A和C是对应点，B和D是对应点，可得AB+BD=14，最后得出结果．【详解】解：∵图形平移后，对应点连成的线段平行且相等，∴AB平移到线段CD，点A平移到点C，则A和C是对应点，B和D是对应点，∴AC=BD，AB=CD∵AC+BD+AB+CD=2AB+2BD=28，∴AB+BD=14，∵AB=6cm，∴BD=14-6=8cm，故答案为：8．【点睛】根据平移的性质，图形平移后，对应点连成的线段平行且相等，求出结果．5、60°或60度【解析】【分析】由邻补角的定义，结合2ABD CBD ∠∠＝，可得答案.【详解】解：2,180,ABD CBD ABD CBD ∠∠∠+∠=︒＝118060.3CBD ∴∠=⨯︒=︒ 故答案为：60︒【点睛】本题考查的是邻补角的定义，掌握“互为邻补角的两个角的和为180︒”是解本题的关键.三、解答题1、（1）见解析；（2）见解析【分析】（1）根据要求作出图形即可．（2）根据要求作出图形即可．【详解】解：（1）根据题意得：AD 是长为4，宽为3的长方形的对角线，所以在点C 右上方长为4，宽为3的长方形的对角线所在的直线与AD 平行，如图，直线CE 即为所求作．（2）根据题意得：CD 是长为6，宽为3的长方形的对角线，所以在点B 右下方长为6，宽为3的长方形的对角线所在的直线与CD 垂直，如图，直线BF 即为所求作．【点睛】本题主要考查了画平行线和垂线，熟练掌握平行线和垂线的画法是解题的关键．2、∠BOC的补角有两个∠BOD和∠AOC；∠BOC的邻补角为∠AOC；∠BOC没有对顶角.【分析】由题意直接根据补角，邻补角及对顶角的定义进行分析即可找出.【详解】解：因为∠BOC＋∠AOC=180º(平角定义），所以∠AOC是∠BOC的补角,∠AOD=∠BOC（已知），所以∠BOC＋∠BOD=180º.所以∠BOD是∠BOC的补角．所以∠BOC的补角有两个：∠BOD和∠AOC.因为∠AOC和∠BOC相邻，所以∠BOC的邻补角为：∠AOC.∠BOC没有对顶角.【点睛】本题考查补角，邻补角及对顶角的定义，熟练掌握补角，邻补角及对顶角的定义是解题的关键.3、（1）∠AOD=36°，∠BOD=144°；（2）∠BOE=54°【分析】（1）先由BOD∠的度数是AOD∠的4倍，得到∠BOD=4∠AOD，再由邻补角互补得到∠AOD+∠BOD=180°，由此求解即可；（2）根据垂线的定义可得∠DOE=90°，则∠BOE=∠BOD-∠DOE=54°．【详解】解：（1）∵BOD∠的度数是AOD∠的4倍，∴∠BOD=4∠AOD，又∵∠AOD+∠BOD=180°，∴5∠AOD=180°，∴∠AOD=36°，∴∠BOD=144°；（2）∵OE⊥CD，∴∠DOE=90°，∴∠BOE=∠BOD-∠DOE=54°．【点睛】本题主要考查了垂线的定义，邻补角互补，熟练掌握邻补角互补是解题的关键．4、见详解【分析】根据垂直的定义及平行线的性质与判定可直接进行求解．【详解】证明：AB CD⊥（已知），⊥，FG AB∴∠=∠=︒（垂直的定义）90BDC BFGCD GF ∴∥（同位角相等，两直线平行）23∴∠=∠（两直线平行，同位角相等）又12∠=∠（已知）13∠∠∴=（等量代换）DE BC ∴∥（内错角相等，两直线平行）．【点睛】本题主要考查垂直的定义及平行线的性质与判定，熟练掌握垂直的定义及平行线的性质与判定是解题的关键．5、（1）图见解析，53，5；（2）图见解析，3．【分析】（1）先根据点的移动得到点M ，再连接点,O M 可得线段OM ，然后测量角的度数和线段OM 的长度即可得；（2）先画出线段AB ，再根据垂线的尺规作图画出垂线PD ，然后测量PD 的长即可得．【详解】解：（1）如图，线段OM 即为所求．此时M 点在点O 的北偏东53︒方向上，O 、M 两点的距离是5cm ，故答案为：53，5；（2）如图，线段AB和垂线PD即为所求．测得点P到AB的距离是3cm，故答案为：3．【点睛】本题考查了测量角的大小、线段的长度、作线段和垂线，熟练掌握尺规作图的方法是解题关键．。
人教版七年级数学下册第五章相交线与平行线复习训练题
第五章相交线与平行线类型一邻补角与对顶角巧分辨1.如图1所示的几个图形中，能构成对顶角的是( )图12．如图2，三条直线AB，CD，EF相交于点O，则∠1的邻补角为______________．图23．如图3，直线AB，CD交于点O，射线OM平分∠AOC.若∠BOD＝76°，求∠AOM的度数．图3类型二区分同位角、内错角、同旁内角有原则4.如图4，与∠1构成内错角的是( )图4A．∠2 B．∠3 C．∠4 D．∠55．如图5，直线DE经过点C，则∠A的内错角是________，∠A的同旁内角是________________．图56．如图6，E是AB延长线上一点，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？(1)∠A和∠D；(2)∠A和∠CBA；(3)∠C和∠CBE.图6类型三掌握相交的特殊情形——垂直7．如图7，已知AB，CD相交于点O，OE⊥CD，垂足为O，∠AOC＝30°，则∠BOE等于( )图7A ．30°B ．60°C ．120°D ．130°8.如图8所示，在直角三角形ABC 中，∠ACB＝90°，CD⊥AB 于点D ，则点A 到BC 的距离为线段______的长度；点A到CD 的距离为线段______的长度；点C 到AB 的距离为线段______的长度．图8类型四 平行线的判定和性质9.如图9，直线a ，b 被直线c 所截，下列说法正确的是( )A ．当∠1＝∠2时，一定有a∥bB ．当a∥b 时，一定有∠1＝∠2C ．当a∥b 时，一定有∠1＋∠2＝90°D ．当∠1＋∠2＝180°时，一定有a∥b10．如图10，已知AB∥CD，∠1＝60°，则∠2＝________°.图9图1011.如图11，不添加辅助线，请你写出一个能判定EB∥AC的条件：________________________．图1112．如图12，AB∥CD，直线EF交AB于点E，交CD于点F，EG平分∠BEF，交CD于点G，∠1＝50°，求∠2的度数．图1213．如图13，已知∠1＋∠2＝180°，∠DEF＝∠A，试判断∠ACB与∠DEB的大小关系，并说明理由．图1314．如图14所示，已知OP∥QR∥ST，连接PR，SR，猜想∠1，∠2，∠3三个角之间的关系，并说明理由．图14类型五命题与定理须细辨15．下列语句不是命题的是( )A．若a<0，b<0，则ab>0B．用三角板画一个60°的角C．对顶角相等D．互为相反数的两个数的和为016．下列命题中，是真命题的是( )A．对顶角相等B．同位角相等C．若a2＝b2，则a＝bD．若a>b，则－2a>－2b17．将下列命题改写成“如果……那么……”的形式．(1)直角都相等；(2)末位数字是5的整数能被5整除；(3)三角形的内角和是180°.类型六平移平移的特征：图形的平移变换中，图形的形状、大小、方向都不发生改变，只是改变了图形的位置；平移前后图形的对应点的连线平行(或在同一条直线上)且相等．18．下列现象中，不属于平移的是( )A．钟表的指针转动B．电梯的升降C．火车在笔直的铁轨上行驶D．传送带上物品的运动19．如图15，将周长为8的三角形ABC沿BC方向向右平移1个单位长度得到三角形DEF，则四边形ABFD的周长为( )图15A．6 B．8 C．10 D．12类型七方程思想在几何中的应用20．如图16，已知a∥b，∠1＝(3x＋70)°，∠2＝(5x＋22)°，求∠1的补角的度数．图16类型八开放型问题21．给出下列三个论断：①∠B＋∠D＝180°；②AB∥CD；③BC∥DE.请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论”栏中，使之成为一道由已知可得到结论的题目，并说明理由．已知：如图17，________________________．结论：________________________．图17类型九探究型问题22．【阅读材料】在“相交线与平行线”的学习中，有这样一道典型问题：如图18①，AB∥CD，点P在AB与CD之间，可得结论：∠BAP＋∠APC＋∠PCD＝360°.理由如下：过点P作PQ∥AB.∴∠BAP＋∠APQ＝180°.∵AB∥CD，PQ∥AB，∴PQ∥CD，∴∠PCD＋∠CPQ＝180°.∴∠BAP＋∠APC＋∠PCD＝∠BAP＋∠APQ＋∠CPQ＋∠PCD＝180°＋180°＝360°.【问题解决】(1)如图②，AB∥CD，点P在AB与CD之间，可得∠BAP，∠APC，∠PCD间的等量关系是________________________________________________________________________；(2)如图③，AB∥CD，点P ，E 在AB 与CD 之间，AE 平分∠BAP，CE 平分∠DCP，写出∠AEC 与∠APC 间的等量关系，并写出理由；(3)如图④，AB∥CD，点P ，E 在AB 与CD 之间，∠BAE＝13∠BAP，∠DCE＝13∠DCP ，可得∠AEC与∠APC 间的等量关系是________________________．图18答案1．D2.∠BOE 和∠AOF 3．解：∵∠BOD＝76°， ∴∠AOC＝∠BOD＝76°. ∵射线OM 平分∠AOC，∴∠AOM＝12∠AOC＝12×76°＝38°.4．B5.∠ACD ∠ACB，∠ACE 和∠B6．解：(1)∠A 和∠D 是直线AE ，DC 被直线AD 所截而成的同旁内角． (2)∠A 和∠CBA 是直线AD ，BC 被直线AE 所截而成的同旁内角． (3)∠C 和∠CBE 是直线DC ，AE 被直线BC 所截而成的内错角． 7．C 8.AC AD CD 9．D 10.12011．答案不唯一，如∠C＝∠EBD 12．解：∵AB∥CD，∴∠2＝∠BEG，∠BEF＋∠1＝180°. ∵∠1＝50°，∴∠BEF＝130°. ∵EG 平分∠BEF，∴∠BEG＝12∠BEF＝65°， ∴∠2＝65°.13．解：∠ACB＝∠DEB.理由：∵∠1＋∠2＝180°，∠1＋∠DFE＝180°，∴∠2＝∠DFE，∴AB∥EF，∴∠DEF＝∠BDE.∵∠DEF＝∠A，∴∠A＝∠BDE，∴AC∥DE，∴∠ACB＝∠DEB.14．解：∠2＋∠3＝180°＋∠1.理由：∵OP∥QR，∴∠2＋∠QRP＝180°，∴∠QRP＝180°－∠2.∵QR∥ST，∴∠3＝∠QRS＝∠1＋∠QRP＝∠1＋180°－∠2.∴∠2＋∠3＝180°＋∠1.15．B16. A17．解：(1)如果几个角是直角，那么它们都相等．(2)如果一个整数的末位数字是5，那么它能被5整除．(3)如果一个图形是三角形，那么它的内角和是180°.18．A19. C20．解：如图，因为a∥b，所以∠1＝∠3.又因为∠1＝(3x＋70)°，∠2＝(5x＋22)°，∠2＋∠3＝180˚，所以(3x ＋70)°＋(5x＋22)°＝180°，解得x＝11，所以∠1＝(3x＋70)°＝103°.又因为180°－103°＝77°，所以∠1的补角的度数为77°.21．解：答案不唯一，符合题意的情况有3种，即①②→③；①③→②；②③→①，任选其中一种即可．已知：如图17，∠B＋∠D＝180°，AB∥CD.结论：BC∥DE.理由：因为AB∥CD，所以∠B＝∠C(两直线平行，内错角相等)．又因为∠B＋∠D＝180°，所以∠C＋∠D＝180°，所以BC∥DE(同旁内角互补，两直线平行)．22．解：(1)如图②，作PE∥AB，得∠APE＝∠BAP.∵AB∥CD，AB∥PE，∴CD∥PE，∴∠CPE＝∠PCD，∴∠APC＝∠APE＋∠CPE＝∠BAP＋∠PCD.故答案为∠APC＝∠BAP＋∠PCD.(2)∠APC＝2∠AE C.理由：设∠EAB＝∠EAP＝x，∠ECD＝∠ECP＝y.由(1)可知：∠AEC＝x＋y，∠APC＝2x＋2y，∴∠APC＝2∠AE C.(3)设∠EAB＝a，∠DCE＝b，则∠BAP＝3a，∠DCP＝3b. 由题意得∠AEC＝a＋b，∠APC＋3a＋3b＝360°，∴∠APC＋3∠AEC＝360°.故答案为∠APC＋3∠AEC＝360°.。
第五章相交线与平行线练习题2022-2023学年人教版七年级数学下册+
人教版七年级下册第五章相交线与平行线练习题一．垂线（共3小题）1．如图，直线AB⊥CD于点O，EF为过点O的一条直线，∠1＝50°，则∠2的度数是（）A．40°B．50°C．25°D．130°2．如图，AG平分∠BAC，∠BED＝∠C，∠1+∠2＝90°．（1）求证：FH⊥DE；（2）若∠3＝∠4，∠BAC＝66°，求∠DFH的度数．3．已知直线AB与CD相交于点O，EO⊥CD于点O，∠DOF＝2∠AOF，若∠BOE＝42°，求∠DOF的度数．二．同位角、内错角、同旁内角（共1小题）4．如图，直线l1、l2、l3两两相交于点A、B、C，生成如图所示的∠1～∠12的12个小于平角的角中，互为同位角、内错角、同旁内角的对数分别记为a、b、c，则a+b+c的值为（）A．18B．24C．30D．36三．平行线的性质（共15小题）5．如图，a∥b，将一块直角三角板的30°角的顶点放在直线b上，若∠1＝46°，则∠2的度数是（）A．76°B．104°C．106°D．114°6．一块含30°角的直角三角板和直尺如图放置，若∠1＝146°，则∠2的度数为（）A．56°B．116°C．64°D．74°7．如图，直线AB∥ED，且∠1＝70°，则∠2的度数为（）A．95°B．100°C．110°D．120°8．如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE＝α，∠DCE＝β．下列各式：①α+β，②α﹣β，③β﹣a，④360°﹣α﹣β，∠AEC的度数可能是（）A．②③B．①④C．①③④D．①②③④9．如图，AB∥CD，则下列各式子计算结果等于180度的是（）A．∠1+∠2+∠3B．∠1+∠2﹣∠3C．∠1﹣∠2+∠3D．∠2﹣∠1+∠3 10．直角三角板ABC与直角三角板DEF如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AC与DE相交于点M．若BC∥EF，则∠CME的大小为（）A．75°B．80°C．85°D．90°11．如图，AB∥CD，CE交AB于点F，若∠C＝60°，则∠AFE的度数为（）A．120°B．125°C．130°D．135°12．如图，AB∥CD，点E是AB上一点，点F是CD上一点，FG平分∠EFD，且∠BEF＝116°，则∠EGF的度数是（）A．25°B．30°C．32°D．42°13．如图，l1⊥l3，l2∥l4，l3，l4，l1交于一点，若∠1＝37°，则∠2的度数为（）A．37°B．53°C．60°D．63°14．如图，在直角三角形ABC中，∠C＝90°，点D在AB上，点G在BC上，△BDG沿直线DG翻折到△FDG位置，DF与BC交于点E，如果DF∥AC，那么∠B与∠BDG的数量关系是．15．如图，AB∥CD，AE∥CF，若∠A＝40°，则∠C的度数为．16．如图是一款长臂折叠LED护眼灯示意图，EF与桌面MN垂直，当发光的灯管AB恰好与桌面MN平行时，∠DEF＝120°，∠BCD＝110°，则∠CDE的度数为°．17．如图，若AB∥ED，∠ABC＝30°，∠BCD＝55°，那么∠D＝．18．如图，点D在三角形ABC的边BC上，DE∥AC交AB于点F，若∠E＝∠C，试说明∠B＝∠EAB．19．把一块长方形木板与一块含30°的直角三角板如图放置，若∠DEG＝34°，求∠BFE 的度数．四．平行线的判定与性质（共1小题）20．完成下面的证明过程：已知：如图，∠D＝123°，∠EFD＝57°，∠1＝∠2．求证：∠3＝∠B证明：∵∠D＝123°，∠EFD＝57°（已知）∴∠D+∠EFD＝180°∴∥（）又∵∠1＝∠2（已知）∴∥（内错角相等，两直线平行）∴∥（）∴∠3＝∠B．（两直线平行，同位角相等）五．平移的性质（共1小题）21．如图，Rt△ABC和Rt△DEF重叠在一起，将△DEF沿点B到点C的方向平移到如图位置，已知AB＝14．图中阴影部分的面积为84，DH＝4，则平移距离为．六．作图-平移变换（共1小题）22．如图是10×8的正方形网格，每个小正方形的边长为1，其顶点称为格点．请按要求在图中画出格点三角形（顶点均在格点上）．（1）平移格点三角形ABC，画出平移后的格点三角形EFG（点A，B，C的对应点分别为点E，F，G），使点D落在线段EF上；（2）三角形EFG的面积为．。
人教版七年级数学第五章相交线与平行线专题训练题(含解析)
相交线与平行线专题训练题1、如图1，AB∥CD，在AB、CD内有一条折线EPF．（1）求证：∠AEP+∠CFP=∠EPF．（2）如图2，已知∠BEP的平分线与∠DFP的平分线相交于点Q，试探索∠EPF 与∠EQF之间的关系．（3）如图3，已知∠BEQ=∠BEP，∠DFQ=∠DFP，则∠P与∠Q有什么关系，说明理由．（4）已知∠BEQ=∠BEP，∠DFQ=∠DFP，有∠P与∠Q的关系为∠P+n∠Q=360°．（直接写结论）（1）证明：如图1，过点P作PG∥AB，，∵AB∥CD，∴PG∥CD，∴∠AEP=∠1，∠CFP=∠2，又∵∠1+∠2=∠EPF，∴∠AEP+∠CFP=∠EPF．（2）如图2，，由（1），可得∠EPF=∠AEP+CFP，∠EQF=∠BEQ+∠DFQ，∵∠BEP的平分线与∠DFP的平分线相交于点Q，∴∠EQF=∠BEQ+∠DFQ=（∠BEP+∠DFP）==，∴∠EPF+2∠EQF=360°．（3）如图3，，由（1），可得∠P=∠AEP+CFP，∠Q=∠BEQ+∠DFQ，∵∠BEQ=∠BEP，∠DFQ=∠DFP，∴∠Q=∠BEQ+∠DFQ=（∠BEP+∠DFP）=[360°﹣（∠AEP+∠CFP）]=×（360°﹣∠P），∴∠P+3∠Q=360°．（4）由（1），可得∠P=∠AEP+CFP，∠Q=∠BEQ+∠DFQ，∵∠BEQ=∠BEP，∠DFQ=∠DFP，∴∠Q=∠BEQ+∠DFQ=（∠BEP+∠DFP）=[360°﹣（∠AEP+∠CFP）]=×（360°﹣∠P），∴∠P+n∠Q=360°．故答案为：∠P+n∠Q=360°．2、如图，直线AB、CD相交于点O，OE平分∠BOD．（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；（2）若OF平分∠COE，∠BOF=15°，若设∠AOE=x°．①则∠EOF=．（用含x的代数式表示）②求∠AOC的度数．解：（1）由对顶角相等可知：∠BOD=∠AOC=70°，∵∠FOB=∠DOF﹣∠BOD，∴∠FOB=90°﹣70°=20°，∵OE平分∠BOD，∴∠BOE=∠BOD=×70°=35°，∴∠EOF=∠FOB+∠BOE=35°+20°=55°，（2）①∵OE平分∠BOD，∴∠BOE=∠DOE，∵∠BOE+∠AOE=180°，∠COE+∠DOE=180°，∴∠COE=∠AOE=x，∵OF平分∠COE，∴∠FOE=x，故答案为：；②∵∠BOE=∠FOE﹣∠FOB，∴∠BOE=x﹣15°，∵∠BOE+∠AOE=180°，∴x﹣15°+x=180°，解得：x=130°，∴∠AOC=2∠BOE=2×（180°﹣130°）=100°．3、已知如图所示，∠B=∠C，点B、A、E在同一条直线上，∠EAC=∠B+∠C，且AD平分∠EAC，试说明AD∥BC的理由．解：理由是：∵AD平分∠EAC，∴∠1=∠EAC，∵∠EAC=∠B+∠C，∠B=∠C，∴∠C=∠EAC，∴∠C=∠1，∴AD∥BC．4、阅读下面的推理过程，在括号内填上推理的依据，如图：因为∠1+∠2=180°，∠2+∠4=180°（已知）所以∠1=∠4，（同角的补角相等）所以a∥c．（内错角相等，两直线平行）又因为∠2+∠3=180°（已知）∠3=∠6（对顶角相等）所以∠2+∠6=180°，（等量代换）所以a∥b．（同旁内角互补，两直线平行）所以b∥c．（平行与同一条直线的两条直线平行）解：因为∠1+∠2=180°，∠2+∠4=180°（已知），所以∠1=∠4，（同角的补角相等）所以a∥c．（内错角相等，两直线平行）又因为∠2+∠3=180°（已知）∠3=∠6（对顶角相等）所以∠2+∠6=180°，（等量代换）所以a∥b．（同旁内角互补，两直线平行）所以b∥c．（平行与同一条直线的两条直线平行）．故答案为：同角的补角相等；内错角相等，两直线平行；对顶角相等；等量代换；同旁内角互补，两直线平行；平行与同一条直线的两条直线平行．5、已知：如图，AB∥CD，FE⊥AB于G，∠EMD=134°，求∠GEM的度数．解：作EN∥CD，如图所示：则∠EMD+∠MEN=180°，∴∠MEN=180°﹣134°=46°，∵FE⊥AB，∴∠FGB=90°，∵AB∥CD，∴EN∥AB，∴∠GEM=90°+46°=136°．6、已知AD∥BC，AB∥CD，E为射线BC上一点，AE平分∠BAD．（1）如图1，当点E在线段BC上时，求证：∠BAE=∠BEA．（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE=3∠CDE，∠AED=60°．①求证：∠ABC=∠ADC；②求∠CED的度数．（1）证明：∵AE平分∠BAD，∴∠BAE=∠EAD，∵AD∥BC，∴∠AEB=∠EAD，∴∠BAE=∠BEA；（2）①证明：∵AD∥BC，AB∥CD，∴四边形ABCD是平行四边形，∴∠ABC=∠ADC；②解：∵∠ADE=3∠CDE，设∠CDE=x°，∴∠ADE=3x°，∠ADC=2x°，∵AB∥CD，∴∠DAB=180°﹣2x°，∵∠DAE=∠BAE=∠BEA=90°﹣x°，又∵AD∥BC，∴∠BED+∠ADE=180°，∵∠AED=60°，即90﹣x+60+3x=180，∴∠CDE=x°=15°，∠ADE=45°，∵AD∥BC，∴∠CED=180°﹣∠ADE=135°．7、如图，AB∥DC，增加折线条数，相应角的个数也会增多，∠B，∠E，∠F，∠G，∠D之间又会有何关系？解：如图1，作EM∥AB，FN∥AB，GP∥AB，∵AB∥DC，∴EM∥FN，FN∥GP，GP∥DC，∴∠B=∠1，∠2=∠3，∠4=∠5，∠6=∠D，∴∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6，∴∠B+∠F+∠D=∠E+∠G．8、（1）如图，直线a，b，c两两相交，∠3=2∠1，∠2=155°，求∠4的度数．（2）如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOE=4：1，求∠AOF的度数．解：（1）如图，∵∠2=155°，∴∠1=180°﹣∠2=180°﹣155°=25°，∴∠3=2∠1=2×25°=50°，∵∠3=∠4，（对顶角相等）∴∠4=50°，（2）∵∠AOD：∠BOE=4：1，∴∠AOD=4∠BOE，∵OE平分∠BOD，∴∠D0E=∠EOB，∴∠AOD+∠DOE+∠BOE=180°，∴6∠BOE=180°，∴∠BOE=∠DOE=30°，∴∠COE=180°﹣30°=150°，∵OF平分∠COE，∴∠EOF=75°，∴∠BOF=∠EOF﹣∠BOE=75°﹣30°=45°，∠AOF=180°﹣45°=135°．9、．如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）说明：∠O=∠BEO+∠DFO．（2）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论．（3）若将折线继续折下去，折三次，折四次…折n次，又会得到怎样的结论？请写出你的结论．（1）证明：过O作OM∥AB，∵AB∥CD，∴AB∥OM∥CD，∴∠BEO=∠MOE，∠DFO=∠MOF，∴∠BEO+∠DFO=∠EOM+∠FOM，即∠EOF=∠BEO+∠DFO．（2）∠BEO、∠O、∠P、∠PFC会满足的关系式是：∠BEO+∠P=∠O+∠PFC，解：过O作OM∥AB，PN∥AB，∵AB∥CD，∴AB∥OM∥PN∥CD，∴∠BEO=∠EOM，∠PFC=∠NPF，∠MOP=∠NPO，∴∠EOP﹣∠OPF=（∠EOM+∠MOP）﹣（∠OPN+∠NPF）=∠EOM﹣∠NPF，∠BEO﹣∠PFC=∠EOM﹣∠NPF，∴∠BEO﹣∠PFC=∠EOP﹣∠OPF，∴∠BEO+∠OPF=∠EOP+∠PFC．（3）解：令折点是1，2，3，4，…，n，则：∠BEO+∠2+∠4+…=∠1+∠3+∠5+…+∠PFC．10、如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．求证：DF∥AB．证明：∵BE是∠ABC的角平分线，∴∠1=∠2，∵∠E=∠1，∴∠E=∠2，∴AE∥BC，∴∠ABC+∠A=180°，∵∠3+∠ABC=180°，∴∠3=∠A，∴DF∥AB．11、如图，已知AB∥CD，EF⊥AB于点G，若∠1=30°，试求∠F的度数．解：作FH∥CD，∴∠HFQ=∠1=30°，又∵∠EGB=90°，∴∠EFH=∠EGB=90°，∴∠EFQ=∠EFH+∠HFQ=120°．答：∠F的度数是120°．12、如图，将一张矩形纸片ABCD沿EF对折，延长DE交BF于点G，若∠EFG=50°，求∠1，∠2的度数．解：如图所示：∵四边形ABCD是矩形，∴∠C=90°，AD∥BC，∴∠3=∠EFG=50°，∠EGF=∠1，由折叠的性质得：∠GDC=∠GEF=∠3=50°，∠EDC=90°，∴∠1=180°﹣50°﹣50°=80°，∴∠EGF=∠1=80°，∴∠2=90°﹣80°=10°．13、如图所示，在长方体中．（1）图中和AB平行的线段有哪些？（2）图中和AB垂直的直线有哪些？解：（1）AB∥A1B1∥C1D1∥CD，即和AB平行的线段有A1B1、C1D1、CD；（2）AB⊥BB1，AB⊥BC，AB⊥AA1，AB⊥AD，AB⊥C1C，AB⊥B1C1，AB⊥A1D1，AB⊥D1D，即和AB垂直的直线有BB1、BC、AA1、AD、C1C、B1C1、A1D1、D1D．。
第五章 相交线与平行线 单元测试(练习)七年级数学下册(人教版)(解析版)
第五章相交线与平行线（满分：100分时间：90分钟）班级_________姓名_________学号_________分数_________一、单选题(共10小题，每小题3分，共计30分)1．如图，直线AB和CD相交于点O，若∠AOC＝125°，则∠BOD等于（）A．55°B．125°C．115°D．65°【答案】B【提示】根据对顶角相等即可求解．【详解】解：∵直线AB和CD相交于点O，∠AOC＝125°，∴∠BOD等于125°．故选B．【点睛】本题主要考查了对顶角的性质，熟知对顶角相等的性质是解题的关键．2．如图，将军要从村庄A去村外的河边饮马，有三条路AB、AC、AD可走，将军沿着AB 路线到的河边，他这样做的道理是（）A．两点之间，线段最短B．两点之间，直线最短C．两点确定一条直线D．直线外一点与直线上各点连接的所有线段中，垂线段最短【答案】D【提示】根据垂线段最短即可完成．【详解】根据直线外一点与直线上各点连接的所有线段中，垂线段最短，可知D 正确故选：D【点睛】本题考查了垂线的性质的简单应用，直线外一点与直线上各点连接的所有线段中，垂线段最短，掌握垂线段最短的性质并能运用于实际生活中是关键．3．点P 是直线l 外一点，,,A B C 为直线l 上三点，4cm,5cm,2cm PA PB PC ===，则点P 到直线l 的距离是（）A ．2cmB ．小于2cmC ．不大于2cmD ．4cm【答案】C【提示】根据“直线外一点到直线上各点的所有线段中，垂线段最短”进行解答．【详解】解：∵直线外一点与直线上各点连接的所有线段中，垂线段最短，且245<<，∴点P 到直线l 的距离不大于2cm ，故选：C ．【点睛】本题考查了垂线段最短的性质，熟记性质是解题的关键．4．如图，直线a ，b 被直线c 所截，下列条件不能判定直线a 与b 平行的是（）A ．∠1＝∠3B ．∠2+∠3＝180°C ．∠1＝∠4D ．∠1+∠4＝180°【答案】D【提示】同位角相等，两直线平行，同旁内角互补，两直线平行，根据平行线的判定方法逐一提示即可.【详解】解：13,a b Ð=Ð\∥Q （同位角相等，两直线平行），故A 不符合题意；∠2+∠3＝180°，a b \∥（同旁内角互补，两直线平行）故B 不符合题意；4=3,1=4,行行Q13,a b \Ð=Ð\∥（同位角相等，两直线平行）故C 不符合题意；∠1+∠4＝180°，1,4∠∠不是同旁内角，也不能利用等量代换转换成同旁内角，所以不能判定,a b ∥故D 符合题意；故选D【点睛】本题考查的是平行线的判定，对顶角相等，掌握“平行线的判定方法”是解本题的关键.5．在下列各题中，属于尺规作图的是（）A ．用直尺画一工件边缘的垂线B ．用直尺和三角板画平行线C ．利用三角板画45︒的角D ．用圆规在已知直线上截取一条线段等于已知线段【答案】D【提示】根据尺规作图的定义：用没有刻度的直尺和圆规作图，只使用圆规和直尺来解决平面几何作图，进行逐一判断即可．【详解】解：A 、用直尺画一工件边缘的垂线，这里没有用到圆规，故此选项不符合题意；B 、用直尺和三角板画平行线，这里没有用到圆规，故此选项不符合题意；C 、利用三角板画45°的角，这里没有用到圆规，故此选项不符合题意；D 、用圆规在已知直线上截取一条线段等于已知线段，是尺规作图，故此选项符合题意；故选D ．【点睛】本题主要考查了尺规作图的定义，解题的关键在于熟知定义．6．在证明命题“若21a >，则1a >”是假命题时，下列选项中所举反例不正确的是（）A ．2a =B ．2a =-C ．3a =-D ．4a =-【答案】A【提示】所谓举反例是指满足命题的条件但不满足命题的结论，由此可判断．【详解】显然A 选项既满足命题的条件也满足命题的结论，故不是举反例，其它三个选项满足命题的条件，但不满足命题的结论，所以都是举反例；故选：A【点睛】本题考查了命题的真假，说明一个命题是假命题要举反例．掌握举反例的含义是关键．7．已知∠α的两边分别平行于∠β的两边．若∠α＝60°，则∠β的大小为（）A ．30°B ．60°C ．30°或60°D ．60°或120°【答案】D【提示】根据题意画图如图（1），根据平行线性质两直线平行，同位角相等，即可得出∠α＝∠1＝∠β，即可得出答案，如图（2）根据平行线性质，两直线平行，同旁内角互补，∠α+∠2＝180°，再根据两直线平行，内错角相等，∠2＝∠β，即可得出答案．【详解】解：如图1，∵a ∥b ，∴∠1＝∠α，∵c ∥d ，∴∠β＝∠1＝∠α＝60°；如图（2），∵a ∥b ，∴∠α+∠2＝180°，∵c ∥d ，∴∠2＝∠β，∴∠β+∠α＝180°，∵∠α＝60°，∴∠β＝120°．综上，∠β＝60°或120°．故选：D ．【点睛】本题主要考查了平行线的性质，熟练掌握相关性质进行计算是解决本题的关键．8．如图，//AB CD ，BF 交CD 于点E ，AE BF ⊥，34CEF ∠=︒，则A ∠的度数是（）A ．34°B ．66°C ．56°D ．46°【答案】C【提示】由余角的定义得出AEC ∠的度数，由两直线平行内错角相等即可得出结论．【详解】解：∵AE BF ⊥，34CEF ∠=︒，∴903456AEC ∠=-= ，∵//AB CD ，∴56A AEC ∠=∠= ，故选：C【点睛】本题考查了平行线的性质和余角，解题的关键是灵活运用所学知识解决问题．9．北京2022年冬奥会会徽是以汉字“冬”为灵感来源设计的．在下面的四个图中，能由图经过平移得到的是（）A ．B ．C ．D ．【答案】B【提示】根据平移只改变图形的位置，不改变图形的形状与大小解答．【详解】解：观察各选项图形可知，B 选项的图案可以通过平移得到．故选：B ．【点睛】本题考查了利用平移设计图案，图形的平移只改变图形的位置，而不改变图形的形状和大小，熟记平移的性质是解决本题的关键．10．如图，平移△ABC 得到△DEF ，其中点A 的对应点是点D ，则下列结论中不成立的是（）A．AD//BE B．AC＝DF C．∠ABE＝∠DEF D．△ABC≌△DEF【答案】C【提示】利用平移的性质解决问题即可．【详解】解：由平移的性质可知：AD∥BE，AC=DF，△ABC≌△DEF，故选项A，B，D正确．故选：C．【点睛】本题考查了平移的性质，解题的关键是熟练掌握平移变换的性质．平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．二、填空题(共5小题，每小题4分，共计20分)11．如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE，∠COF＝36°，则∠BOD的大小为_____．【答案】18°度【提示】根据直角的定义可得∠COE＝90°，然后求出∠EOF，再根据角平分线的定义求出∠AOF，然后根据∠AOC＝∠AOF﹣∠COF求出∠AOC，再根据对顶角相等解答．【详解】解：∵∠COE是直角，∴∠COE＝90°，∵∠COF＝36°，∴∠EOF＝∠COE﹣∠COF＝90°﹣36°＝54°，∵OF平分∠AOE，∴∠AOF＝∠EOF＝54°，∴∠AOC＝∠AOF﹣∠COF＝54°﹣36°＝18°，∴∠BOD＝∠AOC＝18°．故答案为：18°．【点睛】本题考查了对顶角相等的性质，角平分线的定义，是基础题，熟记概念与性质并准确识图，理清图中各角度之间的关系是解题的关键．12．珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，如图，若∠ABC=120°，∠BCD=80°，则∠CDE=__________度．【答案】20【提示】由已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，得AB∥DE，过点C作CF∥AB，则CF∥DE，由平行线的性质可得，∠BCF+∠ABC=180°，所以能求出∠BCF，继而求出∠DCF，又由CF∥DE，所以∠CDE=∠DCF．【详解】解：过点C作CF∥AB，已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，∴AB∥DE，∴CF∥DE，∴∠BCF+∠ABC=180°，∴∠BCF=60°，∴∠DCF=20°，∴∠CDE=∠DCF=20°．故答案为20．【点睛】此题考查的知识点是平行线的性质，关键是过C点先作AB的平行线，由平行线的性质求解．13．如图，AB∥CD，FE⊥DB，垂足为E，∠1＝50°，则∠2的度数是_____．【答案】40°【提示】由EF⊥BD，∠1=50°，结合三角形内角和为180°，即可求出∠D的度数，再由“两直线平行，同位角相等”即可得出结论．【详解】解：在△DEF中，∠1=50°，∠DEF=90°，∴∠D=180°-∠DEF-∠1=40°．∵AB∥CD，∴∠2=∠D=40°．故答案为40°．【点睛】本题考查平行线的性质以及三角形内角和为180°，解题关键是求出∠D=40°．解决该题型题目时，根据平行线的性质，找出相等或互补的角是解题技巧．14．如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD 的周长为_____________．【答案】10．【详解】试题解析：根据题意，将周长为8的△ABC沿边BC向右平移1个单位得到△DEF，则AD=1，BF=BC+CF=BC+1，DF=AC，又∵AB+BC+AC=10，∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10．15．如图，AB∥CD，∠B=160°，∠D=120°，则∠E=_________【答案】40°【提示】延长AB 交DE 于F ，由平行线的性质得出同位角相等∠EFB=∠D=120°，再由三角形的外角性质即可求出∠E 的度数．【详解】解：延长AB 交DE 于F ，∵AB ∥CD ，∠D=120°，∴∠EFB=∠D=120°，∴∠E=∠B-∠EFB=40°．故答案为40°．【点睛】本题考查平行线的性质、三角形的外角性质；熟练掌握平行线的性质，并能进行推理计算是解题关键．三、解答题(共5小题，每小题10分，共计50分)16．如图，直线AB ，CD 相交于点O ，OE 平分AOD ∠，OF OC ⊥，()1图中AOF ∠的余角是______(把符合条件的角都填出来)；()2如果AOC 160∠= ，那么根据______可得BOD ∠=______度；()3如果132∠= ，求2∠和3∠的度数．【答案】（1）∠BOC 、∠AOD （2）对顶角相等，160（3）26°【详解】试题提示：（1）根据互余两角和为90°，结合图形找出即可；（2）从图形中可知∠AOC和∠DOB为对顶角，直接可求解；（3）根据角平分线可求∠AOD的度数，然后根据对顶角和邻补角可求解.试题解析：（1）图中∠AOF的余角是∠BOC、∠AOD（把符合条件的角都填出来）；（2）如果∠AOC=160°，那么根据对顶角相等可得∠BOD=160度；（3）∵OE平分∠AOD，∴∠AOD=2∠1=64°，∴∠2=∠AOD=64°，∠3=90°﹣64°=26°．17．如图，直线CD与直线AB相交于C，根据下列语句画图、解答．（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由【答案】（1）见解析；（2）见解析；（3）∠PQC=60°，理由见解析【详解】解：如图所示：（1）画出如图直线PQ（2）画出如图直线PR（3）∠PQC=60°理由是：因为PQ∥CD所以∠DCB+∠PQC=180°又因为∠DCB=120°所以∠PQC=180°－120°=60°18．如图，已知AM∥BN，∠A=60°，点P是射线M上一动点（与点A不重合），BC，BD 分别平分∠ABP和∠PBN，分别交射线AM于点C，D,（1）∠CBD=（2）当点P运动到某处时，∠ACB=∠ABD，则此时∠ABC=（3）在点P运动的过程中，∠APB与∠ADB的比值是否随之变化？若不变，请求出这个比值：若变化，请找出变化规律．【答案】（1）60°；（2）30°；（3）不变．【提示】（1）由AM∥BN可得∠ABN=180°-∠A，再由BC、BD均为角平分线可求解；（2）由AM∥BN可得∠ACB=∠CBN，再由∠ACB=∠ABD可得∠ABC=∠DBN；（3）由AM∥BN可得∠APB=∠PBN，再由BD为角平分线即可解答.【详解】解：（1）∵AM∥BN，∴∠ABN=180°﹣∠A=120°，又∵BC，BD分别平分∠ABP和∠PBN，∴∠CBD=∠CBP+∠DBP=12（∠ABP+∠PBN）=12∠ABN=60°，故答案为60°．（2）∵AM∥BN，∴∠ACB=∠CBN，又∵∠ACB=∠ABD，∴∠CBN=∠ABD，∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN，∴∠ABC=∠CBP=∠DBP=∠DBN，∴∠ABC=12∠ABN=30°，故答案为30°．（3）不变．理由如下：∵AM∥BN，∴∠APB=∠PBN，∠ADB=∠DBN，又∵BD 平分∠PBN ，∴∠ADB=∠DBN=12∠PBN=12∠APB ，即∠APB ：∠ADB=2：1．【点睛】本题考查了平行线的性质.19．如图，将△ABC 沿着从B 到D 的方向平移后得到△EDF ，若AB=16cm ，AE=12cm ，CE=4cm ．（1）指出△ABC 平移的距离是多少？（2）求线段BD 、DE 、EF 的长．【答案】(1)12cm ；（2）BD =12cm ，DE =16cm ，EF =8cm ．【提示】（1）找准平移前后的对应点即可确定平移的距离；（2）根据平移的性质分别求得相应的线段的长即可．【详解】（1）∵AE =12cm ，∴平移的距离=AE =12cm ；（2）∵三角形ABC 沿着从B 到D 的方向平移后得到三角形EDF ，∴BD =AE =12cm ，DE =AB =16cm ，EF =AC =AE ﹣CE =16﹣4=8（cm ）．【点睛】本题考查了平移的性质，熟练掌握平移的性质，数形结合，准确识图是解题的关键．20．已知：直线AB CD ∥，点M 、N 分别在直线AB ，CD 上，点E 为平面内一点．（1）如图，AME ∠，E ∠，ENC ∠的数量关系是__________．（2）利用（1）的结论解决问题：如图，已知30AME ∠=︒，EF 平分MEN ∠，NP 平分ENC ∠，EQ NP ，求FEQ 得度数．（3）如图，点G 为CD 上一点，AMN m EMN ∠=∠，GEK m GEM ∠=∠，EH MN 交AB 于点H ，直接写出GEK ∠，BMN ∠，GEH ∠之间的数量关系．（用含m 的式子表示）【答案】（1）E AME ENC∠=∠+∠（2）15FEQ ∠=︒（3）180BMN KEG m GEH ∠+∠-∠=︒【解析】整体提示：(1)过E 作EH AB ，结合平行公理和平行线的性质即可得到AME ∠，E ∠，ENC ∠的数量关系；(2)直接利用(1)中的结论，结合角平分线的定义及平行线的性质即可；(3)利用平行线的性质和角平分线的定义及角的和差关系建立GEK BMN m GEH ，，∠∠∠之间的数量关系.解：（1）过E 作EH AB ．∵AB CD ，∴EH AB CD ，∴AME MEH ∠=∠，HEN ENC ∠=∠，∴MEN MEH HEN∠=∠+∠AME ENC =∠+∠，即：MEN AME ENC ∠=∠+∠．（2）∵EF 平分MEN ∠，EP 平分ENC ∠，∴12FEN MEN ∠=∠，12ENP ENC ∠=∠，∵30AME ∠=︒，由（1）结论可知，∴MEN AME ENC∠=∠+∠30ENC =︒+∠，∴12FEN MEN ∠=∠()1302ENC =︒+∠1152ENC =︒+∠15ENP =︒+∠．∵EQ PN ，∴QEN ENP ∠=∠，又∵FEN FEQ QEN∠=∠+∠FEQ ENP =∠+∠，∴15ENP FEQ EMP ︒+∠=∠+∠，∴15FEQ ∠=︒．（3）GEK ∠，BMN ∠，GEH ∠之间的数量关系是180GEK BMN m GEH ∠+∠-∠=︒．∵GEK m GEM ∠=∠，AMN m EMN ∠=∠，∴1GEM GEK m ∠=∠，1EMN AMN m∠=∠，∵EH MN ，∴1HEM EMN AMN m∠=∠=∠，∵GEH GEM HEM∠=∠-∠11GEK AMN m m=∠-∠，∴m GEH GEK AMN ∠=∠-∠，∵180BMN AMN ∠=︒-∠，∴180AMN BMN ∠=︒-∠，∴180m GEH GEK BMN ∠=∠-︒+∠，∴180GEK BMN m GEH ∠+∠-∠=︒．。
第5章《相交线与平行线》 大题专项提升训练：平行线的判定和性质(含答案)
人教版七年级下册第5章《相交线与平行线》大题专项提升训练平行线的判定和性质1．如图，AE平分∠BAD，DF平分∠CDA，且AE∥DF，求证：AB∥CD．2．如图，AD⊥CB于D，EF⊥CB于F，∠1＝∠2，∠BAC＝70°，求∠AGD的度数．3．如图，已知∠1+∠2＝180°，∠3＝108°．求∠4的度数．4．如图，已知AB＝CD，∠1＝∠2．求证：BC＝DA．5．如图，∠1＝∠2，∠C＝∠D．求证：∠A＝∠F．6．如图，已知∠1+∠2＝180°，∠DEF＝∠A，试判断∠ACB与∠DEB的大小关系，并对结论进行说明．7．已知：如图，C，D是直线AB上两点，∠1+∠2＝180°，DE平分∠CDF，EF∥AB，（1）求证：CE∥DF；（2）若∠DCE＝130°，求∠DEF的度数．8．如图，D，E分别是三角形ABC的边AB，BC上的点，DE∥AC，点F在DE的延长线上，且∠DFC＝∠A．（1）求证：AB∥CF；（2）若∠ACF比∠BDE大40°，求∠BDE的度数．9．如图，在△ABC中，EF⊥AB，CD⊥AB．（1）求证：EF∥CD；（2）若点G在AC边上，∠1＝∠2，求证：∠DGC+∠GCB＝180°．10．如图，在三角形ABC中，AD⊥BC于点D，点E是AB上一点，EF⊥BC于点F，点G是AC上一点，连接DG，且∠1＝∠2．求证：AB∥DG．11．如图，在三角形ABC中，AD⊥BC，EF⊥BC，垂足分别为D、F．G为AC上一点，E为AB上一点，∠1＝∠2．求证：DG∥AB．12．如图，在三角形ABC中，EF⊥AB，∠ADG＝∠B，若点G在AC边上，∠1＝∠2，判断CD与AB的位置关系，并说明理由．13．如图，在三角形ABC中，∠1＝∠2，点E，F，G分别在BC，AB，AC上，且EF⊥AB，GD∥BC交AB于点D．请判断CD与AB的位置关系，并说明理由．14．如图，在三角形ABC中，点D、F在边BC上，点E在边AB上，点G在边AC上，AD∥EF，∠1+∠FEA＝180°．求证：∠CDG＝∠B．15．如图，在三角形ABC中，CD⊥AB，垂足为点D，F为BC上的点，FG⊥AB，垂足为点G，点E在AC上，连接DE，若∠EDC＝∠BFG．求证：∠B＝∠ADE．16．如图，在三角形ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H，∠CDG＝∠B，∠1+∠FEA＝180°．（1）EH与AD平行吗？请说明理由；（2）若∠BAD＝30°，求∠H的度数．17．如图，在三角形ABC中，点D，F在边BC上，点E在边AB上，点G在边AC上，EF与GD的延长线交于点H，∠1＝∠B，∠2+∠3＝180°．（1）判断EH与AD的位置关系，并说明理由．（2）若∠DGC＝58°，且∠H＝∠4+10°，求∠H的度数．参考答案1．【解答】证明：∵AE平分∠BAD，DF平分∠CDA，∴∠DAE＝∠BAD，∠ADF＝∠CDA又∵AE∥DF，∴∠DAE＝∠ADF，∴∠BAD＝∠CDA，∴AB∥CD．2．【解答】解：∵EF∥AD（已知），∴∠2＝∠3（两直线平行，同位角相等）；∵∠1＝∠2（已知），∴∠1＝∠3（等量代换）；∴DG∥AB（内错角相等，两直线平行）．∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补）．∵∠BAC＝70°，∴∠AGD＝110°．3．【解答】解：给图中各角标上序号，如图所示．∵∠1+∠2＝180°，∠2+∠5＝180°，∴∠1＝∠5，∴AB∥CD，∴∠3＝∠6．∵∠4+∠6＝180°，∠3＝108°，∴∠4＝180°﹣108°＝72°．4．【解答】证明：在△ABC与△CDA中，，∴△ABC≌△CDA（SAS），∴BC＝DA．5．【解答】证明：∵∠1＝∠2，∠2＝∠3，∴∠1＝∠3．∴BD∥CE．∴∠ABD＝∠C．又∠C＝∠D，∴∠D＝∠ABD．∴DF∥AC．∴∠A＝∠F．6．【解答】解：∠ACB与∠DEB相等，理由如下：证明：∵∠1+∠2＝180°（已知），∠1+∠DFE＝180°（邻补角定义），∴∠2＝∠DFE（同角的补角相等），∴AB∥EF（内错角相等两直线平行），∴∠BDE＝∠DEF（两直线平行，内错角相等），∵∠DEF＝∠A（已知），∴∠BDE＝∠A（等量代换），∴DE∥AC（同位角相等两直线平行），∴∠ACB＝∠DEB（两直线平行，同位角相等）．7．【解答】（1）证明：∵∠1+∠2＝180°，C，D是直线AB上两点，∴∠1+∠DCE＝180°，∴∠2＝∠DCE，∴CE∥DF；（2）解：∵CE∥DF，∠DCE＝130°，∴∠CDF＝180°﹣∠DCE＝180°﹣130°＝50°，∵DE平分∠CDF，∴∠CDE＝∠CDF＝25°，∵EF∥AB，∴∠DEF＝∠CDE＝25°．8．【解答】（1）证明：∵DE∥AC，∴∠BDE＝∠A，∵∠DFC＝∠A，∴∠DFC＝∠BDE，∴AB∥CF．（2）解：∵DE∥AC，∴∠ACF+∠DFC＝180°，由（1）中已证∠DFC＝∠BDE，∴∠ACF+∠BDE＝180°，又∵∠ACF比∠BDE大40°，∴∠BDE+40°+∠BDE＝180°，∴∠BDE＝70°．9．【解答】证明：（1）∵EF⊥AB，CD⊥AB，∴∠BFE＝∠CDB＝90°，∴EF∥CD；（2）∵EF∥CD，∴∠2＝∠BCD，∵∠1＝∠2，∴∠1＝∠BCD，∴DG∥BC，∴∠DGC+∠GCB＝180°．10．【解答】证明：∵EF⊥BC，AD⊥BC，∴EF∥AD，∴∠1＝∠BAD，∵∠1＝∠2，∴∠BAD＝∠2，∴AB∥DG．11．【解答】证明：∵AD⊥BC，EF⊥BC，∴∠ADB＝∠EFB＝90°，∴AD∥EF，∴∠2＝∠3，∵∠1＝∠2，∴∠1＝∠3，∴DG∥AB．12．【解答】解：CD⊥AB．理由如下：∵∠ADG＝∠B，∴DG∥BC，∴∠1＝∠DCB，∵∠1＝∠2，∴∠2＝∠DCB，∴CD∥EF，∴∠CDB＝∠EFB，∵EF⊥AB，∴∠EFB＝90°，∴∠CDB＝90°，∴CD⊥AB．13．【解答】解：CD⊥AB．理由如下：∵DG∥BC，∴∠1＝∠DCB．∵∠1＝∠2，∴∠2＝∠DCB．∴CD∥EF．∴∠CDB＝∠EFB．∵EF⊥AB，∴∠EFB＝90°．∴∠CDB＝90°．∴CD⊥AB．14．【解答】证明：∵AD∥EF，（已知），∴∠2＝∠3，（两直线平行，同位角相等），∵∠1+∠FEA＝180°，∠2+∠FEA＝180°，∴∠1＝∠2（同角的补角相等），∴∠1＝∠3（等量代换），∴DG∥AB（内错角相等，两直线平行），∴∠CDG＝∠B．（两直线平行，同位角相等）．15．【解答】证明：如图所示：∵FG⊥AB，CD⊥AB，∴∠FGB＝∠CDB＝90°，∴FG∥CD，∴∠BFG＝∠BCD，又∵∠EDC＝∠BFG，∴∠BCD＝∠EDC，∴DE∥BC，∴∠B＝∠ADE．16．【解答】解：（1）平行，理由如下：∵∠CDG＝∠B，∴AB∥DG，∴∠BAD＝∠1，∵∠1+∠FEA＝180°，∴∠BAD+∠FEA＝180°，∴EH//AD；（2）由（1）得EH//AD，∠1＝∠BAD，∴∠H＝∠1，∴∠BAD＝∠H，∵∠BAD＝30°，∴∠H＝30°．17．【解答】解：（1）EH∥AD，理由如下：∵∠1＝∠B，∴AB∥GD，∴∠2＝∠BAD，∵∠2+∠3＝180°，∴∠BAD+∠3＝180°，∴EH∥AD；（2）由（1）得AB∥GD，∴∠2＝∠BAD，∠DGC＝∠BAC，∵∠DGC＝58°，∴∠BAC＝58°，∵EH∥AD，∴∠2＝∠H，∴∠H＝∠BAD，∴∠BAC＝∠BAD+∠4＝∠H+∠4＝58°，∵∠H＝∠4+10°，∴∠4+10°+∠4＝58°，解得：∠4＝24°，∴∠H＝34°．。
七年级数学下册第五章《相交线与平行线》测试卷-人教版(含答案)
七年级数学下册第五章《相交线与平行线》测试卷-人教版（含答案）三总分题号一二19 20 21 22 23 24分数一、选择题(每题3分，共30分)1．下列四个图案中，可能通过如图平移得到的是（）A．B．C．D．2．下列说法正确的是（）A．直线AB和直线BA是同一条直线 B．直线是射线的2倍C．射线AB与射线BA是同一条射线 D．三条直线两两相交，有三个交点3．下列各图中，∠1＝∠2一定成立的是（）A．B．C．D．4．如图，直线BC，DE相交于点O，AO⊥BC于点O．OM平分∠BOD，如果∠AOE ＝50°，那么∠BOM的度数（）A．20°B．25°C．40°D．50°5．如图，在铁路旁有一李庄，现要建一火车站，为了使李庄人乘车最方便，请你在铁路线上选一点来建火车站，应建在（）A．A点B．B点C．C点D．D点6．如图，点P在直线L外，点A，B在直线l上，PA＝3，PB＝7，点P到直线l 的距离可能是（）A．2 B．4 C．7 D．87．如图所示，∠1和∠2不是同位角的是（）A．①B．②C．③D．④8．如图所示，同位角共有（）A．6对B．8对C．10对D．12对9．下列说法正确的有（）个．①不相交的两条直线是平行线；②在同一平面内，两条不相交的线段是平行线；③过一点可以而且只可以画一条直线与已知直线平行；④如果一条直线与两条平行线中的一条平行，那么它与另一条直线也互相平行．A．1 B．2 C．3 D．410．如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么∠1+∠2+∠3＝（）A ．180°B ．360°C ．270°D ．540°二、填空题(每题3分，共24分)11．把命题“等角的补角相等”改写成“如果…那么…”的形式是______． 12．如图所示，12//l l ，点A ，E ，D 在直线1l 上，点B ，C 在直线2l 上，满足BD 平分ABC ∠，BD CD ⊥，CE 平分DCB ∠，若136BAD =︒∠，那么AEC ∠=___________．13．把一个直角三角板（90GEF ∠=︒，30GFE ∠=︒）如图放置，已知AB ∥CD ，AF 平分BAE ∠，则AEG ∠＝_____________14．如图，点E 在BC 延长线上，四个条件中：①13∠=∠；②25180+=︒∠∠，③4∠=∠B ；④B D ∠=∠；⑤180D BCD ∠+∠=︒，能判断//AB CD 的是______．（填序号）．15．如图，已知12//l l ，直线l 分别与12,l l 相交于,C D 两点，现把一块含30角的直角三角中尺按如图所示的位置摆放．若1130∠=︒，则2∠=___________．16．如图，∠AEM＝∠DFN＝a，∠EMN＝∠MNF＝b，∠PEM＝12∠AEM，∠MNP＝12∠FNP，∠BEP，∠NFD的角平分线交于点I，若∠I＝∠P，则a和b的数量关系为_____（用含a的式子表示b）．17．如图所示，将△ABC沿BC边平移得到△A1B1C1，若BC1＝8，B1C＝2，则平移距离为．18．如图，△ABC的边长AB =3 cm，BC=4 cm，AC=2 cm，将△ABC沿BC方向平移a cm（a＜4 cm），得到△DEF，连接AD，则阴影部分的周长为_______cm．三.解答题(共46分)19．（7分）如图，直线l1，l2，l3相交于点O，∠1＝40°，∠2＝50°，求∠3的度数．20．（7分）已知：如图，AB∥CD，CD∥EF．求证：∠B+∠BDF+∠F＝360°．21．（8分）如图，直线DE与∠ABC的边BC相交于点P，现直线AB，DE被直线BC所截，∠1与∠2．∠1与∠3，∠1与∠4分别是什么角？22.（8分）如图，已知∠1+∠2＝180°，∠3＝∠B．（1）试判断DE与BC的位置关系，并说明理由．（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．23．（8分）图1，点E在直线AB上，点F在直线CD上，EG⊥FG．(1)若∠BEG＋∠DFG＝90°，请判断AB与CD的位置关系，并说明理由；(2)如图2，在(1)的结论下，当EG⊥FG保持不变，EG上有一点M，使∠MFG＝2∠DFG，则∠BEG与∠MFG存在怎样的数量关系？并说明理由；(3)如图2，若移动点M，使∠MFG＝n∠DFG，请直接写出∠BEG与∠MFG的数量关系．24．（8分）已知，E、F分别是直线AB和CD上的点，AB∥CD，G、H在两条直线之间，且∠G＝∠H．（1）如图1，试说明：∠AEG＝∠HFD；（2）如图2，将一45°角∠ROS如图放置，OR交AB于E，OS交CD于F，设K为SO上一点，若∠BEO＝∠KEO，EG∥OS，判断∠AEG，∠GEK的数量关系，并说明理由；（3）如图3，将∠ROS＝（n为大于1的整数）如图放置，OR交AB于E，OS交CD于F，设K为SO上一点，连接EK，若∠AEK＝n∠CFS，则＝．参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CACAAACCDB二、填空题:11．如果两个角是等角的补角，那么它们相等． 12.146° 13．30°解：∵AB ∥CD ，AF 平分∠BAE ， ∴∠BAF=∠EAF=∠AFE ， 又∵∠GFE=30°，∴∠BAF=∠EAF=30°，即∠BAE=60°， ∴∠AEF=180°-60°=120°， 又∵∠GEF=90°，∴∠AEG=120°-90°=30°， 14．②③解：①∵∠1=∠3，∴AD ∥BC ；②∵∠2+∠5=180°，∵∠5=∠AGC ，∴∠2+∠AGC=180°，∴AB ∥DC ； ③∵∠4=∠B ，∴AB ∥DC ； ④∠B=∠D 无法判断出AD ∥BC ； ⑤∵∠D+∠BCD=180°，∴AD ∥BC ． 15．20︒如图，∵121130,l l ∠=︒∥， ∴50CDB ∠=︒， ∵30ADB ∠=︒，∴2503020CDB ADB ∠=∠-∠=︒-︒=︒．16．如图1，ABCD是长方形纸带（AD∥BC），∠DEF＝18°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中的∠CFE的度数是126°．【分析】在图1中，由AD∥BC，利用“两直线平行，内错角相等”可得出∠BFE的度数，由折叠的性质可知，在图3中∠BFE处重叠了三次，进而可得出∠CFE+3∠BFE＝180°，再代入∠BFE的度数即可求出结论．【解答】解：在图1中，AD∥BC，∴∠BFE＝∠DEF＝18°．由折叠的性质可知，在图3中，∠BFE处重叠了三次，∴∠CFE+3∠BFE＝180°，∴∠CFE＝180°﹣3×18°＝126°．故答案为：126°．17．解：∵△ABC沿BC边平移得到△A1B1C1，∴BC＝B1C1，BB1＝CC1，∵BC1＝8，B1C＝2，∴BB1＝CC1＝，即平移距离为3，故答案为：3．18．180；3；内错角相等，两直线平行；两直线平行，同位角相等三.解答题:19．解：∵∠1＝40°，∠2＝50°，∴∠5＝∠1＝40°，∠4＝∠2＝50°，∴∠3＝180°﹣∠5﹣∠4＝180°﹣40°﹣50°＝90°．20．证明：∵AB∥CD（已知）∴∠B+∠BDC＝180°（两直线平行，同旁内角互补）∵CD∥EF（已知）∴∠CDF+∠F＝180°（两直线平行，同旁内角互补）∴∠B+∠BDC+∠CDF+∠F＝360°，∵∠BDF＝∠BDC+∠CDF（已知）∴∠B+∠BDF+∠F＝360°．21．解：∵直线AB，DE被直线BC所截，∴∠1与∠2是同旁内角，∠1与∠3是内错角，∠1与∠4是同位角．22.解：（1）如图1，作直线GH交AB于M，交CD于Q，∵AB∥CD，∴∠BMG＝∠FQH，∵∠EGH＝∠GHF，∴∠AEG＝∠EGH﹣∠BMG＝∠FHG﹣∠FQH＝∠HFD；（2）∠GEK﹣2∠AEG＝45°，如图2，延长KO交AB于M，∵EG∥MS，∴∠AEG＝∠EMF，∠GEK＝∠OKE，设∠OEM＝α，则∠OEK＝2α，∠OME＝45°﹣α，∴∠OKE＝180°﹣∠MEK﹣∠OME＝135°﹣2α，∵EG∥OS，∴∠GEK＝∠OKE＝135°﹣2α，∴∠AEG＝180°﹣∠GEK﹣∠MEK＝180°﹣135°+2α﹣3α＝45°﹣α，即∠GEK﹣2∠AEG＝45°．（3）作OH∥AB，∵AB∥CD，∴OH∥CD，如图3，∵AB∥OH，∴∠OEB＝∠EOH，又∵OH∥CD，∴∠FOH＝∠OFD，又∵∠OFD＝∠CFS＝∠AEK，而∠EOH+∠HOF＝，∴∠EOH ＝﹣∠AEK，即180°﹣n∠EOH＝∠AEK，又∵∠OEK+∠AEK+∠EOH＝180°，∴∠OEK+180°﹣n∠EOH+∠EOH＝180°，∴∠OEK＝（n﹣1）∠EOH，∴，又∵∠EOH＝∠BEO，∴．故答案为：．。
人教版七年级下册数学第五章 相交线与平行线含答案(真题汇编)
人教版七年级下册数学第五章相交线与平行线含答案一、单选题(共15题，共计45分)1、把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（）A.115°B.120°C.145°D.135°2、如图，AE⊥BC于点E，AF⊥CD于点F，则下列哪条线段的长度是表示点A到BC的距离（）A. ADB. AFC. AED. AB3、如图1所示，为了得到点B需将点A向右平移( )A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度4、如图，直线a∥b，直角三角板的直角顶点P在直线b上，若∠1=56°，则∠2为（）A.24°B.34°C.44°D.54°5、如图，直线，，则c与b相交所形成的度数为（）A. B. C. D.6、如图，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H.若∠1＝135°，则∠2的度数为( )A.35°B.45°C.55°D.65°7、如右图，，直线l分别交AB、CD于E、F，，则的度数是( )A.56°B.146°C.134°D.124°8、如图所示：AB∥CD，MN交CD于点E，交AB于F，BE⊥MN于点E，若∠DEM ＝55°，则∠ABE＝（）A.55°B.35°C.45°D.30°9、已知：如图△ABC的顶点坐标分别为A（-4，-3），B（0，-3），C（-2，1），如将B点向右平移2个单位后再向上平移4个单位到达B1点，若设△ABC的面积为S1，△AB1C的面积为S2，则S1， S2的大小关系为（）A.S1＞S2B.S1=S2C.S1＜S2D.不能确定10、如图，已知直线AB∥CD，∠C＝115°，∠A＝25°，则∠E＝( )A.70°B.80°C.90°D.100°11、如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（）A.120°B.130°C.140°D.150°12、如图，已知AB∥CD∥EF，则x、y、z三者之间的关系是（）A.x+y+z=180°B.x+y﹣z=180°C.y﹣x﹣z=0°D.y﹣x﹣2z=0°13、以下各命题中，正确的命题是（）（1）等腰三角形的一边长4 cm，一边长9 cm，则它的周长为17 cm或22 cm；（2）三角形的一个外角，等于两个内角的和；（3）有两边和一角对应相等的两个三角形全等；（4）等边三角形是轴对称图形；（5）三角形的一个外角平分线平行于三角形的一边，那么这个三角形是等腰三角形.A.（1）（2）（3）B.（1）（3）（5）C.（2）（4）（5） D.（4）（5）14、如图，直线a、b被直线c所截，a∥b，∠1=∠2，若∠4=65°，则∠3等于（）A.30°B.50°C.65°D.115°15、如图，将一副三角板按如图放置，∠BAC=∠DAE=90°，∠B=45°，∠E=60°，则下列结论正确的有（）个.①∠1=∠3；②∠CAD+∠2=180°；③如果∠2=30°，则有AC∥DE；④如果∠2=30°，则有BC∥AD.A.4B.3C.2D.1二、填空题(共10题，共计30分)16、如图所示，已知∠1=∠2，请你添上一个适当的条件________ ，使AB∥CD．17、如图，已知AE∥BD，∠1＝126°，∠2＝40°，则∠C＝________°.18、如图，将一块含45°的直角三角板的直角顶点放在直尺的一边上，∠1=75°，则∠2的度数是________．19、如图所示，，若，，则________．20、一副三角板如图摆放，且，则∠1的度数为________．21、如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2=________．22、如图所示，已知BO平分∠CBA，CO平分∠ACB，过O点的直线MN∥BC，若AB=12，AC=14，BC=15,则△AMN的周长为________.23、把点P（1，1）向右平移3个单位长度，再向上平移2个单位长度后的坐标为________．24、命题“锐角与钝角互为补角”的逆命题是________ ．25、如图， AD是的中线，E，F分别是AD和AD延长线上的点，且，连结BF，CE.下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE.其中正确的有________(填上正确的序号)三、解答题(共6题，共计25分)26、如图，直线，相交于点，平分；若，求的度数.27、如图所示，已知在平行四边形ABCD中，BE=DF．求证：∠DAE=∠BCF．28、已知：如图，E、F分别为ABCD的边BC、AD上的点，且∠1=∠2。