2020高考数学 公开课一等奖课件
合集下载
2020高考数学原创.2函数的表示法(二) 公开课一等奖课件

ae bf cg
de bf cg
例3.下列对应关系(A 到 B)中,其中 x∈A, y∈B. (1)A B N , f : x y x 3 ;
(2)A N , B Z , f : x y 2x 3; (3)A { x | 0 x 1}, B { y | y 1},
45
2
60
3
90
2
1
观察下列对应,并思考:
①开平方
3
9
-3
4
2 -2
1
1
-1
1 ②求平方
-1
2
1
-2
4
3 -3
9
③求正弦 1
2
30
2
45
2
60
3
90
2
1
④乘以2 1
1
2 3
2
4
3
5
6
映射的定义:
一般地,设A、B是两个集合,如果 按照某种对应法则f,对于集合A中的 任一个元素,在集合B中都有唯一的元素 和它对应,那么这样的对应(包括A、B 以及A到B的对应法则f )叫做集合A到集 合B的一个映射.
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
2020高考数学理科通用版专题课件一ppt

设 z=x+yi(x,y∈R). 因为 z-i=x+(y-1)i,
所以|z-i|= ������2 + (������-1)2=1, 则 x2+(y-1)2=1.故选 C.
C
关闭
关闭
解-析7-
答案
一、选择题 二、填空题
6.(2019天津卷,文1)设集合A={-1,1,2,3,5},B={2,3,4}, C={x∈R|1≤x<3},则(A∩C)∪B=( )
关闭
由x2-5x<0,得0<x<5.由|x-1|<1,得0<x<2.故“x2-5x<0”是“|x-1|<1”的必要不 充分条件.
关闭
B
解-析9-
答案
一、选择题 二、填空题
8.下列说法正确的是( ) A.“若a>1,则a2>1”的否命题是“若a>1,则a2≤1” B.“若am2<bm2,则a<b”的逆命题为真命题
A.{2}
B.{2,3}
C.{-1,2,3} D.{1,2,3,4}
A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D. D
关闭
关闭
解-析8-
答案
一、选择题 二、填空题
7.(2019天津卷,理3)设x∈R,则“x2-5x<0”是“|x-1|<1”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
C
关闭
关闭
解-析3-
答案
一、选择题 二、填空题
关闭
由 z=-3+2i,得������=-3-2i,则在复平面内������对应的点(-3,-2)位于第三象 限,故选 C.
2020高考数学原创.3椭圆的几何性质 公开课一等奖课件

1
一. 教材分析
(1) 教材的地位和作用 (2) 课时安排
2
一. 教材分析
(一)教材的地位和作用
“椭圆的几何性质”是解析几何研究的 一个重要问题之一。它是学生学习圆锥曲 线所研究的第一个有关性质的内容,其方 法可贯穿于解析几何学习的始终。所以, 通过这部分内容的学习,可以帮助学生更 好的理解解析几何的核心问题------圆锥 曲线的概念,也能为学好后续几种圆锥曲 线作好理论和方法上的准备,是解析几何 中承上启下的关键内容。
6
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行”的和谐统一。结合本节课的具体内容, 参考学习和信息加工模型、广义知识学习阶段和分 类模型,确立教学法。
3
一. 教材分析 (二)课时安排
椭圆几何性质问题研究可安排三课时。本 节作为第一课时,重在研究椭圆的性质。教学 中注重概念的引入,定义的理解。在这个过程 中培养学生分析解决问题的能力,培养学生讨 论交流的合作意识。
4
二. 教法分析
(一)学情分析 (二)教学方法 (三)具体措施
5
二. 教法分析
(一)学情分析
[5]2a 和 2b是什么量? a和 b是什么量? [6]关于离心率讲了几点?
17
标准方程
图象
范围 对称性 顶点坐标 焦点坐标 半轴长 焦距 a,b,c关系 离心率
x2 a2
y2 b2
1(a
b
0)
x2 b2
y2 a2
1(a
一. 教材分析
(1) 教材的地位和作用 (2) 课时安排
2
一. 教材分析
(一)教材的地位和作用
“椭圆的几何性质”是解析几何研究的 一个重要问题之一。它是学生学习圆锥曲 线所研究的第一个有关性质的内容,其方 法可贯穿于解析几何学习的始终。所以, 通过这部分内容的学习,可以帮助学生更 好的理解解析几何的核心问题------圆锥 曲线的概念,也能为学好后续几种圆锥曲 线作好理论和方法上的准备,是解析几何 中承上启下的关键内容。
6
二. 教法分析
(二)教学方法
建构主义认为,知识是在原有知识的基础上, 在人与环境的相互作用过程中,通过同化和顺应, 使自身的认知结构得以转换和发展。元认知理论指 出,学习过程既是认识过程又是情感过程,是“知、 情、意、行”的和谐统一。结合本节课的具体内容, 参考学习和信息加工模型、广义知识学习阶段和分 类模型,确立教学法。
3
一. 教材分析 (二)课时安排
椭圆几何性质问题研究可安排三课时。本 节作为第一课时,重在研究椭圆的性质。教学 中注重概念的引入,定义的理解。在这个过程 中培养学生分析解决问题的能力,培养学生讨 论交流的合作意识。
4
二. 教法分析
(一)学情分析 (二)教学方法 (三)具体措施
5
二. 教法分析
(一)学情分析
[5]2a 和 2b是什么量? a和 b是什么量? [6]关于离心率讲了几点?
17
标准方程
图象
范围 对称性 顶点坐标 焦点坐标 半轴长 焦距 a,b,c关系 离心率
x2 a2
y2 b2
1(a
b
0)
x2 b2
y2 a2
1(a
2020高考数学原创 公开课一等奖课件

以高考为主线,以教材为根本,锁定高考热点,研析命题角 度,点拨方法技巧,融会贯通知识. ○真题感悟·考点整合——明确备考方向,整合知识要点 ○热点聚焦·题型突破——锁定高考热点,研析命题角度 ○归纳总结·思维升华——总结规律方法,防范易错易混 ○专题训练·对接高考——对接高考热点,限时规范训练
第1讲 函数图象与性质及函数与方程
2.函数的性质 (1)单调性:单调性是函数在其定义域上的局部性质.证明函 数的单调性时,规范步骤为取值、作差、变形、判断符号和 下结论.复合函数的单调性遵循“同增异减”的原则; (2)奇偶性:奇偶性是函数在定义域上的整体性质.偶函数的 图象关于y轴对称,在关于坐标原点对称的定义域区间上具 有相反的单调性;奇函数的图象关于坐标原点对称,在关于 坐标原点对称的定义域区间上具有相同的单调性; (3)周期性:周期性也是函数在定义域上的整体性质.若函数 满足f(a+x)=f(x)(a不等于0),则其周期T=ka(k∈Z).
fx-f-x x <0
的解集为
( ).
A.(-2,0)∪(0,2)
B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞) 解析 (1)法一 函数 y=xl|nx||x|的图象过点(e,1),排除 C,D;函
数 y=xl|nx||x|的图象过点(-e,-1),排除 A,选 B.
3.(2014·福建卷)若函数y=logax( a>0,且a≠1)的图象如下图
所示,则下列函数图象正确的是
( ).
解析 因为函数y=logax过点(3,1),所以1=loga 3,解得a=3.y = 3 - x 不 可 能 过 点 (1,3) , 排 除 A ; y = ( - x)3 = - x3 不 可 能 过 点 (1,1),排除C; y=log3(-x)不可能过点(-3,-1), 排除D,故选 B. 答案 B
第1讲 函数图象与性质及函数与方程
2.函数的性质 (1)单调性:单调性是函数在其定义域上的局部性质.证明函 数的单调性时,规范步骤为取值、作差、变形、判断符号和 下结论.复合函数的单调性遵循“同增异减”的原则; (2)奇偶性:奇偶性是函数在定义域上的整体性质.偶函数的 图象关于y轴对称,在关于坐标原点对称的定义域区间上具 有相反的单调性;奇函数的图象关于坐标原点对称,在关于 坐标原点对称的定义域区间上具有相同的单调性; (3)周期性:周期性也是函数在定义域上的整体性质.若函数 满足f(a+x)=f(x)(a不等于0),则其周期T=ka(k∈Z).
fx-f-x x <0
的解集为
( ).
A.(-2,0)∪(0,2)
B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞) 解析 (1)法一 函数 y=xl|nx||x|的图象过点(e,1),排除 C,D;函
数 y=xl|nx||x|的图象过点(-e,-1),排除 A,选 B.
3.(2014·福建卷)若函数y=logax( a>0,且a≠1)的图象如下图
所示,则下列函数图象正确的是
( ).
解析 因为函数y=logax过点(3,1),所以1=loga 3,解得a=3.y = 3 - x 不 可 能 过 点 (1,3) , 排 除 A ; y = ( - x)3 = - x3 不 可 能 过 点 (1,1),排除C; y=log3(-x)不可能过点(-3,-1), 排除D,故选 B. 答案 B
2020年高考数学复习精选课件 第3节 三角函数的图象与性质 公开课一等奖课件
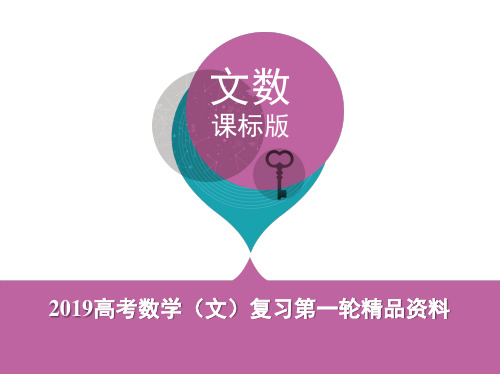
x= 2
sin x
4
≥0,将x- 4 视为一个整体,由正弦函数y=
栏目索引
文数
课标版
2019高考数学(文)复习第一轮精品资料
sin x的图象和性质可知2kπ≤x- ≤π+2kπ,k∈Z.
4
解得2kπ+ 4 ≤x≤2kπ+ 54 ,k∈Z.
所以定义域为x
|
2k
π 4
x
2k
5π 4
,k
Z .
栏目索引
栏目索引
1-2 函数y=sin x-cos x+sin xcos x的值域为
.
答案
1 2
2,1
解析 设t=sin x-cos x,则- 2 ≤t≤ 2 ,t2=sin2x+cos2x-2sin xcos x,则
sin xcos x= 1 t2 , 2
ω3 3 2
∴0<ω<6,且ω= 3 +6k(k∈Z),∴ω=3 ,经检验,满足题意.
2
2
栏目索引
2-2
若函数f(x)=sin ωx
4
(0<ω<1)在 2 ,
上单调递减,求ω的取值范
围.
解析 当 <x<π时,由0<ω<1得 < ω π+ <ωx+ <ωπ+ <5 π,又y=sin x
B.最小正周期为π的偶函数
C.最小正周期为 的奇函数
2
D.最小正周期为 的偶函数
2
(2)函数f(x)=sin x
2020年高考数学复习精选课件 第1节 数列的概念及简单表示法 公开课一等奖课件
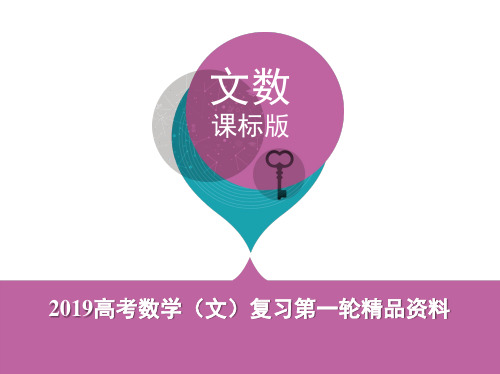
解析 设递推公式an+1=2an+3可以转化为an+1-t=2(an-t),即an+1=2an-t,解得t=
-3.
故an+1+3=2(an+3).
令bn=an+3,则b1=a1+3=5,且
bn1 bn
=
an1 3 an 3
=2.
所以{bn}是以5为首项,2为公比的等比数列.
所以bn=5×2n-1,故an=5×2n-1-3.
栏目索引
文数
课标版
2019高考数学(文)复习第一轮精品资料
栏目索引
文数
课标版
第一节 数列的概念及简单表示法
教材研读
栏目索引
1.数列的定义
按照① 一定顺序 排列的一列数叫做数列,数列中的每一个数叫做这
个数列的② 项 . 2.数列的分类
分类原则
类型
满足条件
按项数分类 有穷数列
项数③ 有限
无穷数列
项数④ 无限
当b≠-1时,an=
3 2
b, n 3n1,
1, n 2.
栏目索引
方法指导 已知Sn求an的三个步骤: (1)先利用a1=S1求出a1; (2)用n-1替换Sn中的n得出Sn-1,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的 表达式; (3)看a1是否符合n≥2时an的表达式,若符合,则可以把数列的通项公式合 写;若不符合,则应该分n=1与n≥2两段来写.
4.数列的通项公式
如果数列{an}的第n项与⑩ 序号n 之间的关系可以用一个式子来表
示,那么这个公式叫做这个数列的通项公式.
5.已知数列{an}的前n项和Sn,
2020高考数学原创.2指数函数及其性质(三) 公开课一等奖课件

作出图象,显示出函数数据表
x
-3 -2 -1 0 1 2 3
y 2 x 0.125 0.25 0.5 1 2 4 8
y 2 x1 0.25 0.5 1 2 4 8 16
y 2 x2 0.5 1 2 4 8 16 32
比较函数
y 2x
y 2x1 y 2x2 的图象关系.
9
比较函数
8
y 2x
7
6
y 2x 1
5
y 2x 1
4
3
的图象关系.
2
1
-4 -2 O
2
4x
(3) y 2 x 1, y 2 x 1. y
9
比较函数
8
y 2x
7
6
y 2x 1
5
y 2x 1
4
3
的图象关系.
2
1
-4 -2 O
2
4x
小 结:
f(x)的图象 向左平移a个单位得到f(x+a)的图象; 向右平移a个单位得到f(x-a)的图象; 向上平移a个单位得到f(x)+a的图象; 向下平移a个单位得到f(x)-a的图象.
性 过点(0,1),即x=0时,y=1
质 在 R 上是增函数
x>0时,ax>1;
在 R 上是减函数
x<0时,0<ax<1
复习引入
指数函数的图象和性质:
a>1
0<a<1
图
y
y=ax y=ax
y
(a>1) (0<a<1)
象
O
x
O
x
定义域 R;值域(0,+∞)
性 过点(0,1),即x=0时,y=1
质 在 R 上是增函数
2020年高考数学复习精选课件 第5节 椭圆 公开课一等奖课件

A. x2 - y2 =1 64 48
B. x2 + y2 =1 48 64
C. x2 - y2 =1 48 64
D. x2 + y2 =1 64 48
(2)已知椭圆C: ax22 + by22 =1(a>b>0)的左、右焦点为F1、F2,离心率为 33 ,过
F2的直线l交C于A、B两点.若△AF1B的周长为4 3 ,则C的方程为
b2
轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE
的中点,则C的离心率为 ( )
A. 1 B. 1 C. 2 D. 3
3
2
3
4
(2)已知动点P(x,y)在椭圆 x2 + y2 =1上,若A点的坐标为(3,0),| AM |=1,且
25 16
PM
· AM
=0,则| PM
所以 2 = 1 ,
ac ac
即2a-2c=a+c,
所以e= c = 1 .故选A.
a3
解法二:如图,设OE的中点为N,
由题意知|AF|=a-c,|BF|=a+c,|OF|=c,|OA|=|OB|=a,
∵PF∥y轴,∴ | MF | = | AF | = a c , | MF | = | BF | = a c , | OE | | AO | a | ON | | OB | a
2.椭圆的标准方程和几何性质
标准方程 图形
xa 22 + by22 =1(a>b>0)
栏目索引
ay22 + xb22 =1(a>b>0)
性质
范围 对称性
顶点 轴 焦距 离心率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.常见的升幂变换是:cos 2α=2cos2 α-1=1-2sin2 α;常见 1-cos 2α 1+cos 2α 2 2 的降幂变换是:sin α= ,cos α= . 2 2 4.利用辅助角公式将含两项的三角函数式化成一个三角函数 的形式:asin α+bcos α= a2+b2sin(α+φ)= a2+b2cos(α-φ),这 是研究三角函数性质的非常重要的思想方法, 也是历年高考的热点 内容. 5.不仅能正用三角公式,而且能逆用和变用公式,也是三角 变换的重要手段.
y=sin
预习测评 1.(2014 年长春一模) 函数 f (x)=(sin x+cos x)2 的一条对称轴的方 程是( )
A.x= 4
B.x= 3
C.x= 2
D.x=π
【答案】A
2.设 a=2sin 24° ,b=2(sin 47° sin 66° -sin 24° sin 43° ),c=sin 85° + 3 cos 95° ,则 a,b,c 的大小关系是( ) A.a>c>b B.b>c>a C.c>b>a D.c>a>b
5 3 10 正解:∵α、β 均为锐角,∴由 sin α= ,cos β= 得 cos α 5 10 2 5 10 = ,sin β= .且 0<α+β<π. 5 10 2 5 3 10 5 10 于是 cos(α+β)=cos αcos β-sin αsin β= · - · = 5 10 5 10 2 .故选 C. 2 答案:C 纠错心得:在经过讨论得到 0<α+β<π 后,仅仅求出 sin(α+β) 的值是不够的,应求 cos(α+β)的值,才能得出正确答案.
2.函数 y=3sin(x-10° )+5sin(x+50° )的最大值是( 11 A.8 B.7 C. 34 D. 12
)
【答案】B
知识点 3 三角变换的综合应用 【例 3】 已知 sin α+sin β+sin γ=0,cos α+cos β+cos γ=0, 则 cos(β-γ)=( ) 1 1 A.- B. C.-1 D.1 2 2 思路点拨:将 sin α 和 cos α 移到右边,两式分别平方后相加 即可得答案.
【答案】-2
知识点 2
辅助角公式 asin x+bcos x= a2+b2sin(x+φ)=
a2+b2cos(x-φ)的应用 1 2 3 【例 2】 已知函数 y= cos x+ sin xcos x+1.x∈R. 2 2 (1)当自变量 y 取得最大值时,求自变量 x 的集合; (2)求函数的单调递增区间. 思路点拨:将函数变形成 y=Asin(ωx+φ)+B 的形式再求解.
错解: 5 3 10 ∵sin α= ,cos β= . 5 10 2 5 10 ∴cos α= ,sin β= . 5 10 5 3 10 2 5 10 于是,sin(α+β)=sin αcos β+cos αsin β= · + · 5 10 5 10 2 = .故选 A. 2 2 错因分析:在得到 sin(α+β)= 后,应讨论 α+β 的范围. 2
Байду номын сангаас
解: 1 2 3 1 1+cos 2x 3 1 (1)y=2cos x+ 2 sin xcos x+1=2× + 2 ×2sin 2x+ 2 5 1 π 5 1 3 1 1=2 sin 2x+ cos 2x+4=2sin2x+6+4. 2 2 π π π 当函数 y 取得最大值时,2x+6=2kπ+2(k∈Z)即 x=kπ+6(k π ∈Z).故 y 取得最大值时,自变量 x 的集合为x|x=6+kπ,k∈Z. π π π π π (2)由 2kπ-2≤2x+6≤2kπ+2(k∈Z),得 kπ-3≤x≤kπ+6(k π π ∈Z),故函数的单调递增区间是kπ-3,kπ+6(k∈Z).
典例剖析 知识点 1 利用三角变换求值 【例 1】 不查表计算 tan 54° -tan 36° -2tan 18° =________. 思路点拨: 注意 54° +36° =90° , 54° =36° +18° , 36° =2×18° , 尝试用三角变换的公式进行变形求解.
【答案】 0
cos 10° 1.化简(tan 10° - 3) =________. sin 50°
【答案】D
3.cos 75° =________.
6- 2 【答案】 4
tan 45° +tan 15° 4. =________. 1-tan 15°
【答案】
3
要点阐释 1. 半角公式可如下进行推导, 由 cos 2α=cos2 α-sin2α 的变形 cos 1-cos 2α 2 2 2 2α=2cos α-1 及 cos 2α=1-2sin α 得到 sin α= 及 cos2α= 2 1+cos 2α 1-cos α α α , 再以 代替 α、 以 α 代替 2α 即可得到 sin =± ; 2 2 2 2 1+cos α α α cos = ± , 最 后 将 这 两 个 式 子 相 除 就 得 到 tan = 2 2 2 1-cos α α ± .特别要注意,公式前的“± ”号由 所在的象限确定,如 2 1+cos α α α α=240° 时, =120° ,sin 应该为正. 2 2 2.进行三角恒等变换主要看式子的特点,从名称与角上整体把 握,根据角与名称选择适当公式解决.
课堂总结 1.常数代换是三角恒等变换的一个重要手段,如 1=sin2 α+ 1 1 π 2 π π cos2α、 =sin 30° 、 =cos 、 =sin =cos . 2 2 3 2 4 4 2.角的变换是解答某些试题的关键,常见的角变换有:α=(α α+β α-β +β)-β=β-(β-α), β= - , 2α=(α+β)+(α-β)=(α+β) 2 2 α -β α+β β α β α -(β-α), =α- - -β, =α+ - +β. 2 2 2 2 2 2
自学导引
1-cos α α α ± 2 ; 1.用 cos α 表示 的正弦、余弦、正切是:sin =_________ 2 2 1+cos α 1-cos α ± α α ± 2 1+cos α cos =__________;tan =______________. 2 2
2.几个公式的变形: 1-cos α 2 α ①sin = ; 2 2 1+cos α 2 α ②cos = ; 2 2 1-cos α 2α ③tan = ; 2 1+cos α 1-cos α α sin α ④tan = = . 2 1+cos α sin α
自主探究 用什么方法才能求函数
y=sin
1 1 x+ cos x+ 的最值? 2 2
1 1 x+2cos x+2的最值,先将 y 解: 用三角变换能求 1 1 1 1 = sin x+2 cos x+2 化为 y=sin xcos x+2(sin x+cos x)+4, π 然后令 sin x+cos x=t,即 t= 2sinx+4,可见- 2≤t≤ 2. t2-1 t2-1 1 1 1 12 3 于是 sin xcos x= 2 ,y= 2 +2t+4=2t+2 -8. 1 3 故当 t=-2时,函数有最小值-8; 3+2 2 当 t= 2时,函数有最大值 4 .
方法点评:根据两个已知等式及待求式子 cos(β-γ)的特点, 应将 sin α 和 cos α 移到右边, 再平方后将其消去. 在得到 1+2(cos 1 βcos γ+sin βcos γ)+1=1,即 cos βcos γ+sin βsin γ=- 后,逆用 2 公式 cos(α-β)=cos αcos β+sin αsin β 就得到正确答案.
【解析】由 sin α+sin β+sin γ=0,cos α+cos β+cos γ=0 得, sin β+sin γ=-sin α,cos β+cos γ=-cos α.将这两个等式两边分 别平方得,sin2 β+2sin βsin γ+sin2 γ=sin2α,cos2β+2cos βcos γ+ cos2γ=cos2α. 两式相加得,1+2(cos βcos γ+sin βsin γ)+1=1,得 cos(β-γ) 1 =- .故选 A. 2 【答案】A
3.在△ABC 中,3sin A+4cos B=6,且 4sin B+3cos A=1, 则 C 的大小为( ) A.30° B.150° C.30° 或 150° D.60° 或 120°
【答案】A
误区解密 不考虑角的范围而出错 5 3 10 【例题】 设 α、β 均为锐角,且 sin α= ,cos β= ,则 5 10 α+β 的值为( ) π 3π 3π π π A. 或 B. C. D.2kπ+ (k∈Z) 4 4 4 4 4
