理论力学6-1 质点运动微分方程

合集下载

高等教育出版社_金尚年_马永利编著的理论力学课后习题答案

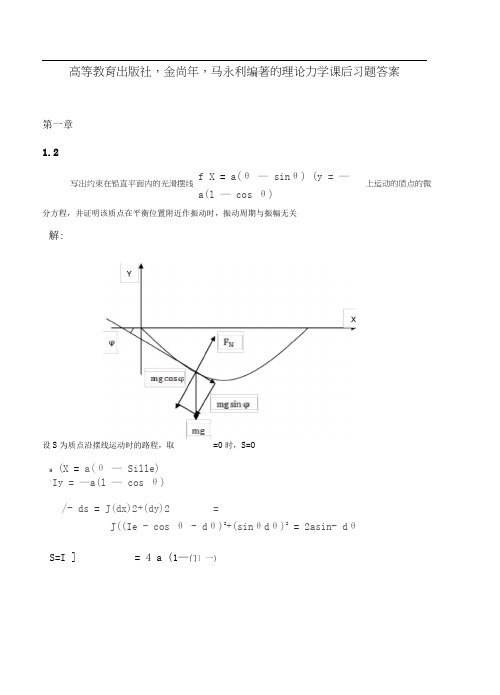
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2f X = a(θ — sinθ) (y = —a(l — cos θ)分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关解:设S 为质点沿摆线运动时的路程，取=0时，S=OH (X = a(θ — Sille) ,Iy = —a(l — cos θ) /- ds = J(dx)2+(dy)2=J((Ie - cos θ - dθ)2+(sinθdθ)2= 2asin- dθS=I ]= 4 a (1—门〕一)写出约束在铅直平面内的光滑摆线上运动的质点的微S = 2acosθ-θ + 2asiιι-θ = a cos - θ2+ 2a Sin-θ2 2 2 2 2设:为质点所在摆线位置处切线方向与 X 轴的夹角，取逆时针为正，L 二弔即切线斜率dy COS θ -1tan φ = — = ——dx sιnθ受力分析得:InS = —mg sin φ = mg cos yΩ .. Ω . - Ω 则1 ' : . 一，此即为质点的运动微分方程。

2 2 t52S =鲁(S — 4a)Λ (S - 4a) + ~(β — 4a) = 01.3证明：设一质量为m 的小球做任一角度Λ的单摆运动运动微分方程为m(L ∙2L )=F ,mr J - mg Sin给式两边同时乘以LdV-gsind^ 对上式两边关于T 积分得1L 2=gcos*c2利用初始条件V - J 0时V - 0故c = -g COS 71由可解得日=-* JC o S - c o So上式可化为-\：丰∙Jcos 日-CoS 日0 日=Zdt・s - 4a —周期性变化的函数，周期T = 2π该质点在平衡位置附近作振动时，振动周期与振幅无关，为进一步化简可得sin 2? —sin 22°由于上面算的过程只占整个周期的1/4故由 Sin /sin - = Sin2 2两边分别对二「微分可得COSEdV - Sin -cos ：:d ：:2 2COSAJIYin 学sin^Sin -cos tP故dr -2 ------- 2 d ‘ I I-Si n 2 电 Si n2 CP \ 2 由于Or VvO 故对应的0 <2—CoSe ∕J 1 —s in 2电 S in 2 申2 2d 「Sin cos : 2故T =4l 2-- d其中 K 2=sin 2玉Y g J 1—K 2sin 2 半2通过进一步计算可得T 仔1 [1 (1* (jκ-(1 3 5 (2n」)*「•]Vg 22江42^4><6汇…Tne 二 Sin 2 2 两边同时积分可得701故T =2.2^0 ■Sin Si n —2 21.5M 为地球的质量；可知，地球表面的重力加速度 g , X 为取地心到无限远的广义坐标,【I ：二 Ill- 「，②联立①，②可得:岂仃；,M 为地球的质量；③解:如图，在半径是R 的时候，由万有引力公式, 对表面的一点的万有引力为PMm* 一 ,①R a当半径增加,R2=R+jl ,此时总质量不变，仍为M,此时表面的重力加速度1可求:由④得:对⑥式进行通分、整理后得：AGM ΔR 3+2ΔRR8 =R 7 CR+ΔR)2A2ΔR R 2AR⑧则当半径改变J N 时，表面的重力加速度的变化为:A2ΔRR2AR =S —。

理论力学第11章质点运动微分方程

必须指出，牛顿定律中涉及到物体的运动与作用在物体上的力。显然，物体及其所受的力不因参考系的选择而改变，但同一物体的运动在不同的参考系中的描述可能是完全不同的，这就存在着根本性的矛盾。这决定了牛顿定律不可能适用于一切参考系，而只能适用于某些参考系。凡牛顿定律成立的参考系，称为惯性参考系。凡牛顿定律成立的参考系，称为惯性参考系凡牛顿定律成立的参考系
2 d 2ρ dϕ m 2 −ρ = Fρ dt dt 2 d ρ dϕ d ϕ m 2 + ρ 2 = Fϕ dt dt dt
（11.6）
这就是极坐标形式的质点运动微分方程。
11.3 质点动力学的两类基本问题
应用质点运动微分方程，可以求解质点动力学的两类基本问题。第一类基本问题已知质点的运动规律，即已知质点的运动方程或质点在任意瞬时的速度或加速度，求作用在质点上的未知力。这一类问题可归结为数学中的微分问题。求解该问题比较简单。若已知质点的运动方程，则只须将它对时间求两次导数即可得到质点的加速度，代入适当形式的质点运动微分方程，得到一个代数方程组，求解这个方程组即可得到所求的未知力。
11.1 动力学基本定律
质点动力学的基本定律是牛顿在总结前人特别是伽利略的研究成果的基础上，1687年在其著作《自然哲学的数学原理》中提出来的，通常称为牛顿三定律牛顿三定律。这些牛顿三定律定律是动力学的基础。
11.1 动力学基本定律
第一定律任何质点都保持其静止的或作匀速直线运动的状态，动的状态，直到它受到其他物体的作用而被迫改变这种状态为止。种状态为止质点保持静止或匀速直线运动状态的属性称为惯性惯性，惯性质点作匀速直线运动称为惯性运动，因此第一定律又称惯性运动，惯性运动惯性定律。此定律表明：质点必须受到其他物体的作用惯性定律时，也就是受到外力的作用时，才会改变其运动状态，即外力是改变质点运动状态的原因外力是改变质点运动状态的原因。外力是改变质点运动状态的原因

《理论力学动力学》第十六讲变质量质点的运动微分方程

变质量动力学曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、变质量质点的运动微分方程2、变质量动力学在火箭发射中的应用3、变质量质点的动力学普遍定理1、变质量质点的运动微分方程(1) 变质量质点的运动微分方程m 在时刻t ，质点的质量为m ，速度为vv 1在时刻t+d t ，并入速度为v 1的微小质量d mm +d m v 并入后，系统质量变为m +d m ，速度变为v +质点系在t 瞬时的动量：11d m m =+×p v v t +d t 质点系在t+d t 瞬时的动量：2(d )(d )m m =++p v v 根据动量定理有：(e)21d d t=-=p p p F (e)1d d d d d d m m m m t+×+×-×=v v v v F 略去高阶微量d m ·d v ，并在等式两边同时除以d t , 得：(e)1d d ()d d m m t t --=v v v F 式中v 1-v=v r 为微小质量在并入前相对于质点m 的相对速度, 令d d r m t f =F v 则有：(e)d d m tf =+v F F —变质量质点的运动微分方程方程形式与常质量质点运动微分方程相似，仅在右端多了一项F ϕ，它具有力的量纲，常称为反推力。

当d m /d t >0 时，F ϕ与v r 同向；当d m /d t <0 时，F ϕ与v r 反向。

1、变质量质点的运动微分方程(2) 常用的几种质量变化规律i 质量按线性规律变化1)1(0<-=t t m m b b ，由知，其反推力为：b 0d d m t m-=r 0rd d mm t f b ==-F v v 当v r 为常量时，反推力也为常量，且与v r 方向相反。

ii 质量按指数规律变化tm m b -=e 0由知，其反推力为：0d d t m m e t b b -=-r 0rd d tmm e t b f b -==-F v v 令a ϕ表示仅在反推力F ϕ作用下变质量质点的加速度，则：0rrtt m e m m e b f f b b b ---===-F v a v 当v r 为常量时，a ϕ也为常量，即由反推力引起的加速度为常量。

《理论力学》第10章质心运动定理

第10章质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力，受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章质心运动定理
18
例题图示机构，均质杆OA长l，质量为m1，滑块A的质量为m2，滑道CD的质量为m3。OA杆在一力偶（图中未画出）作用下作匀角度ω转动。试求O处的水平约束反力（机构位于铅直平面
内，各处摩擦不计）。 C
A
O
E
D
★理论力学电子教案
第10章质心运动定理
第10章质心运动定理
27
ma A
第10章质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章质心运动定理
§2 质点系动量、冲量
质点动量：质点系动量：
p mv
P mivi mvC
问：刚体系动量？
元冲量：
dI F dt
冲量：
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章质心运动定理
1
第十章质心运动定理&动量定理
★理论力学电子教案
第10章质心运动定理

第9章质点动力学的基本方程

PAG 15
Northeastern University
§9-2 质点的运动微分方程
质量为m的炮弹以速度发射, 的炮弹以速度v 例9-2 质量为的炮弹以速度 0发射,v0与地面夹角为θ,求炮弹的运动规律。弹的运动规律。以炮弹为研究对象，解:⑴ 以炮弹为研究对象，画受力图取坐标系， ⑵ 取坐标系，列微分方程
PAG 17
Northeastern University
§9-2 质点的运动微分方程
质量为m的小球以水平速度射入静水,如水对小球的的小球以水平速度v 例9-3 质量为的小球以水平速度 0 射入静水如水对小球的阻力F与小球速度的方向相反,而大小成正比与小球速度v的方向相反而大小成正比,即阻力与小球速度的方向相反而大小成正比即F=-µv（µ为粘（为粘滞阻尼系数）。忽略水对小球的浮力, ）。忽略水对小球的浮力滞阻尼系数）。忽略水对小球的浮力,试分析小球在重力和阻力作用下的运动。力作用下的运动。以小球为研究对象，解:⑴ 以小球为研究对象，画受力图取直角坐标系, ⑵ 取直角坐标系,列小球沿 x、y轴的运动微分方程、轴的运动微分方程 r r r F = − µvx i − µv y j
理论力学
Northeastern University
第九章质点动力学的基本方程
静力学：研究物体在力系作用下的平衡条件运动学：研究物体运动的几何性质动力学：研究物体的机械运动与作用力之间的关系质点：只计质量而忽略其形状和大小的物体
研究卫星的轨道时，卫星刚体作平移时，刚体质点；质点。
PAG 2
µ
m
t
PAG 20
Northeastern University

质点动力学的基本方程

y aC x ar
FS
maa Fi m(ae ar aC ) Fi
φ
F
a
n e
φ FN
mg
沿x方向投影: m (a r aen ) F mg sin Fs 2 ( 0.2) F 2 9.8 sin57.3o Fs (1) 沿y方向投影: maC FN mg cos
t m m y D2 e g ( 6) m m m C1 v 0 C 2 v0 0 可得 m2 m2 0 D1 2 g D2 2 g
t m 代入( 3) , (5) 式整理可得: x v0 (1 e m )

t m2 m m y 2 g(e 1) gt
k cos v x 1 0
例三
质量为m 的小球以水平速度vo 射入静水中. 水对小球的阻力F与小球的速度方向相反, 而大小为F = μv , μ 为阻尼系数. 忽略水对小球的浮力. 求小球在重力和阻力作用下的运动方程.
解：
O vo F M v mg x
y
取质点分析其受力及运动： 0 m x 0 C x Ct D x x eA cos kt m y
m x
0
vo
F
v
e A cos kt y m e y A sin kt E km e y 2 A cos kt Et F k m
0 (1) x m g ( 2) m y mg y y y m 先求二阶常系数齐次的通解 x m x x （特征根法） 0 m 1 0 2 m

第4章理论力学习题解

4.1一质点受一与距离成反比的引力作用在一直线上运动，质点的质量为m ，比例系数为k ，如此质点从距原点O 为a 的地方由静止开始运动，求其到达O 点所需的时间。

解：质点受引力为：xk F -=，其运动微分方程为：xk tm-=d d v （1）即： x k xm -=d d v v分离变量积分：⎰⎰-=x axx k m d d 0v v vxa k m ln212=v)ln(2d d xa mk tx -==v （2）（v 与x 反向，取负值） )ln00ln ),0((∞→→>∴∈xa x xa a x令：y ayex aex xa y yyd 2d )ln(22---===，代入（2）式得；mk ty aey2d d 22-=-分离变量积分：)0:0:(∞→→y a x⎰⎰=-∞t yt mk y ea 0d 2d 22t mk a22π2=故到达O 点所需的时间为： km a t 2π=4.2一质点受力3K xa x F +-=作用，求势能)(x V 与运动微分方程的解。

解：C x a x x xa x x F x V ++=+--=-=⎰⎰2232K 21d )K (d )(适当选取势能零点，使0=C ，则222K 21)(xa x x V +=机械能 =++=2222K 2121xa x xm E 常量（1）将（1）改写成2222K 242xa x E xm --= （2）质点运动微分方程：32K xa x xm +-= 22K 22xa x xmx +-=⇒ （3）（3）+（2）得22K 44)(2x E xx x m -=+ 即0)K(K 4d d 2222=-+E x mtx （4）（4）式通解：⎪⎪⎭⎫⎝⎛++=02 K2cos K θt m A Ex当0=x时，222K 21xa x E += 解得KK K)(2max 2a EE x -+=，KK 2aEA -=所以 ⎪⎪⎭⎫⎝⎛+-+=022K2cos KK Kθt m aE E x4.3若质点受有心力作用而在圆θcos 2a r =上运动时，则5228rh ma F -=，式中m 为质量，h 为速度矩。

理论力学(哈工大版)第十章：质点动力学

第六章质点动力学6-1 惯性参考系中的质点动力学一.惯性参考系1.一般工程问题：2.人造卫星、洲际导弹问题：3.天体运动问题：二.牛顿定律1.第一定律（惯性定律）：2.第二定律（力与加速度之间的关系定律）：3.第三定律（作用与反作用定律）：三.质点的运动微分方程将动力学基本方程)(F a m =表示为微分形式的方程，称为质点的运动微分方程。

1.矢量形式（自：会使用微分形式）) )( ( 22方程为质点矢径形式的运动式中t r r F dtr d m == 2.直角坐标形式) )()()( ( 222222运动方程为质点直角坐标形式的式中⎪⎩⎪⎨⎧===⎪⎪⎪⎩⎪⎪⎪⎨⎧===t z z t y y t x x Z dty d m Y dt y d m X dt x d m 3.自然形式b n F F v m F dt s d m ===0222ρτ ), ,,)((轴上的投影轴和轴自然轴系在分别为力运动方程。

为质点的弧坐标形式的式中b n F F F F t s s b n ττ= 四.质点动力学的两类基本问题1.已知质点的运动规律，求作用于质点上的力；----求微分问题。

2.已知质点上所受的力，求质点的运动规律。

----按质点运动的初始条件和力的函数关系对运动微分方程进行求解，从数学角度看，是解微分方程或求积分，并确定相应的积分常数的问题。

第一类问题解题步骤和要点：①正确选择研究对象（一般选择联系已知量和待求量的质点）。

②正确进行受力分析,画出受力图(应在一般位置上进行分析)。

③正确进行运动分析（分析质点运动的特征量）。

④选择并列出适当形式的质点运动微分方程（建立坐标系）。

⑤求解未知量。

2.第二类：已知作用在质点上的力，求质点的运动（积分问题）已知的作用力可能是常力, 也可能是变力。

变力可能是时间、位置、速度或者同时是上述几种变量的函数。

如力是常量或是时间及速度函数时，可直接分离变量积分dt dv 。

理论力学10质点运动微分方程

= mgR 2，于是火箭在任意位置 x 处所受地球引力 F 的大
小为
m g R2 F = x2
(b)
（3）列运动方程求解，由于火箭作直线运动，
火箭的直线运动微分方程式为：m
分离变量积分式(c)
d2 dt
x
2
mg R2 x2
(c)
因为
d d2 tx 2d dv td dv xd dx tvd dv x
其次，定律还指出，若质点的运动状态发生改变，必定是受到其他物体的作用，这种机械作用就是力。
第二定律（力与加速度关系定律）
质点的质量与加速度的乘积，等于作用于质点的力的大小，加速度的方向与力的方向相同。
设质点M的质量为m，所受的力为F，由于力F的
作用所产生的加速度为a，如图10-1所示。则此定律
以上两例都是动力学的第一类基本问题，由此可
归纳出求解第一类问题的步骤如下：
（1）取研究对象并视为质点；（2）分析质点在任一瞬时的受力，并画出受力图；（3）分析质点的运动，求质点的加速度；（4）列质点的运动微分方程并求解。
例10-3 以初速v0自地球表面竖直向上发射一质量为 m 的火箭，如图10-6所示。若不计空气阻力，火箭所
解：取质量块为研究对象，并视其为质点。质
量块沿x方向作直线运动，弹性杆对质量块的作用相当于一弹簧，图10-8（b）是该系统的计算模型。
设弹簧刚度系数
为 k ，任意位置时弹
a
在静力学中，我们研究了力系的简化和平衡问题，但没有研究物体在不平衡力系作用下将如何运动。在运动学中，我们仅从几何学的角度描述了物体的运动规律及其特征，并未涉及物体的质量(Mass)及其所受的力。因此，静力学和运动学都是从不同的侧面研究了物体的机械运动。

岩土基础--理论力学公式

（4）记住三个转动惯量：[1]、均质杆对一端的转动惯量—— J z ml 2 / 3 ； [2]、均质杆对中心轴的转动惯量—— J z ml 2 /12 ； [3]、均质圆盘对中心轴的转动惯量—— J z mR2 / 2 。
动能定理
1、功——W M2 F dr M1
（1）常力在直线运动中的功——W Fs ；
质点的振动
1 固有频率
0 2π f
k m
2 并联弹簧固有频率
0
1 2π
k1 m 2π
k1 k2 m
2 串联弹簧固有频率
1、第二定律（质点动力学基本方程）： F ma
——质点运动微分方程：
m
d2 dt
r
2
F
动量定理
1、质点动量—— p mv
2、质点系动量—— p mivi 或 p mvC （1）质点系动量定理：[1]、微分形式—— dp F edt dI e 或 dp F e ；
dt
[2ቤተ መጻሕፍቲ ባይዱ、积分形式—— p2 p1 I e 。
[2]、速度： v Rω
[3]、加速度： at R ， an v2 / R Rω2 ，
a at2 an2 R 2 ω4 ， tan a, n / ω2 。
二．
轮系的传动比——主动轮 I 与从动轮 II 的角速度的比值 i12
ω1 ω2
R2 R1
z2 z1
质点动力学的基本方程
（2）定轴转动—— Lz J zω 。
3、质点系动量矩定理—— dLO dt
MO (Fi(e) ) ；
——投影式： d Lx dt
M x (Fi(e) ),
d Ly dt
M y (Fi(e) ),
d Lz dt

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

返回
惯性力是体积力
10/16
返回
例 6-2-2 第6章动坐标系Oxyz固结于圆
盘上，研究小球的相对运动。加惯性力：
Se m 2 xi m 2 sj
解
SC Se
12/16
质点动力学
j Sc 2m x
相对运动微分方程：
N
m 2 x mx
N 0 m 2 s 2m x
m sin(0 t )
质点动力学
此时单摆作简谐振动，振动周期只与系统的固有参数有关与振幅无关（等时性）固有参数有关，与振幅无关（等时性）。大振幅情况下，必须求解非线性微分方程，此时单摆的振动不再具有简谐性与等时性。
2 约束力 T mg cos ml
约束力由静约束力和动约束力两部分组成
运动微分方程求解方法
F (t , x, x ) mx
分离变量法
当 F = F(x) 时
dx dx x dx x dx dt d x d t dx
dx F ( x )dx mx
x 1 mx 2 1 mx 2 F ( x )dx （质点动能定理） 2 2 0 x0
6.1 质点运动微分方程
2013年11月12日
2013年11月12日
质点的运动微分方程第 6章

运动微分方程求解方法
分离变量法
矢量式（牛顿第二运动定律）
m rF ma F
第6章质点运动微分方程 mx F (t , x, x )
二阶常微分方程 (t0 ) x 0 初始条件 x(t0 ) x0 , x
解
F m P y
7/16
第 6章
9/16
动力特性分析第6章存在极限速度，即不管
初始条件如何，空气中落体的速度最终趋近于以v = C的速度运动。
11/16
质点动力学
例 6-1-1 分析
mg y 2 my
落体的速度从零开始不断增加，加速度相应地不断减小，必定存在极限速度。当落体以极限速度运动时，重力与空气阻力平衡，据此可求出极限速度
P
ma r F ma e ma c
3/16
惯性力第6章惯性力具有虚假的和真实的两重性
虚假性：
5/16
质点动力学质点动力学
质点动力学
（牵连惯性力）引入 Se mae Sc mac 2mω vr （科氏惯性力）得： mar F Se Sc 质点的相对运动微分方程式在研究质点相对非惯性系的运动时，在形式上仍可使用牛顿第二定律，条件是在真实力之外再加上牵连惯性力和科氏惯性力。
mg sin ml ms
m 2 s
A
mg
x

2 T mg cos ml
14/16
例 6-1-2
mg sin ml
解
2 sin 0, g / l 0 0
第6章
对于微幅振动，对方程线性化
2 0 0
3/16
第 6章
5/16
质点动力学质点动力学
质点动力学
直角坐标系
Fx mx
Fy my
自然坐标系
F ms 2 s m Fn
柱坐标系
2 ) F m(
2 ) F m(
几种特殊情况：当F = F(t) 或F = C时 x dx dt Fdt md x
质点动力学

x
0 x
m dx t t0 ) F (x
6/16
1
例 6-1-1 空气中落体的运动第6章已知：v = 0，空气阻力与速度的平方成正比， 0
比例系数。求：落体运动规律。
例 6-1-1 第6章质点动力学建模步骤
(1) 分析运动，建立合适的坐标系 (2) 质点放在一般位置
ae 2 R cos 2.38 102 m/ s2
质点动力学
6.3 相对地球的运动
ac 2 vr sin 3.39 103 m/ s2
地球自转的影响对一般工程问题影响很小对长时间问题或精度要求较高的问题需考虑其影响
2013年11月12日
2/12
v0 初始条件： t 0, x x0 , x
x(t ) x0 cosh t (v0 / ) sinh t N 2m ( x0 sinh t v0 cosh t ) m 2 s
2
例 6-2-3 第 6章
导杆机构带动单摆的支点O按已知规律x = x0sin t作水平运动。试导出质点m的相对运动微分方程。
2013年11月12日
引言：动力学的任务
第 3篇
动力学建模动力学方程（运动微分方程）：物体运动
引言：惯性参考系
第 3篇在运动学中参考系可以任意选取，但在动力学中则不能任意选取参考系。惯性参考系 —与绝对静止空间固连的参考系以及相对其匀速直线平动的参考系。牛顿定律适用于一切惯性参考系。伽利略相对性原理：一切力学方程和定律对所有惯性参考系都是等价的。惯性系的选取地球参考系 — 一般工程技术问题地心参考系 — 需考虑地球自转影响时日心参考系 — 行星、航天器等
16/16
3
质点在非惯性参考系中的运动第6章问题的提出
6.2 质点在非惯性参考系中的运动
傅科摆：摆动平面变化的单摆北半球的热带气旋牛顿运动定律只适用于惯性坐标系。如何描述质点相对于非惯性坐标系的运动？
质点动力学
2013年11月12日
2/16
质点在非惯性参考系中的运动第 6章
2013/11/12
引言：动力学的地位
第 3篇运动学：研究如何描述物体的运动，不考虑产生运动的原因。静力学：研究作用于物体上的力系的简化与平衡条件，不考虑力系不平衡时物体如何运动。
第3篇
动力学
动力学
运动
力
动力学：以牛顿定律或变分原理为基础，研究力与运动之间的关系。（核心内容）
y
返回
10/16
C2 g ln cosh( t ) g C
返回
神六降落伞
g v C tanh( t ) C
第6章
质点动力学
高空中下落的降落伞，很快达到其极限速度 (约为5m/s)，落地时的冲击只相当于由1.25m 高度跳下时的落地速度。
12/16
高80多米，面积1200平方米，重量仅90多千克。主伞的伞绳直径2.5毫米，一根细绳可以吊起300千克的物体将速度从每秒200米减至每秒6至8米
与其所受力之间的数学关系。力和初始条件
物体
运动规律
第 3篇
动力学动力学
动力学

动力学的两大基本问题：已知力求运动 — 正问题（积分问题）已知运动求力 — 逆问题（微分问题）但常见混合型问题：有未知的运动，也有未知的力。如受约束的非自由质系的动力学问题。
1
第6章质点动力学力

z
O

y
O1 是惯性坐标系(定系) Oxyz 是非惯性坐标系(动系) P 为所研究的质点(动点)，质量为m
O1

x

讨论：什么时候存在科氏惯性力？
4/16
实例分析第6章

歼击机驾驶员的黑晕现象和红视现象等？
既无施力体，也无相应的反作用力，牛顿第三定律不成立。惯性力随坐标系的不同而不同。真实性观察者处于非惯性系中时能感受到惯性力的存在，并可测量。惯性力具有与真实力一样的动力学和静力学效应，在质点的相对运动中可以与实际力一样对待。
8/16
第6章运动初始条件 t 0 : y 0, y 0 0 0
mg y 2 my g v
质点动力学
(3) 分析受力，画受力图 2 P mg g F y (4) 建立运动微分方程： mg y 2 my 定性分析 (5) 数学求解已知力求运动时，需要运动初始条件 (6) 动力特性分析
m
因而磅秤指示增加，人体超重
人工制造失重现象的方法：
落塔飞机的抛物线飞行
在水池中利用水的浮力减
少体重，能模拟宇航员的失重环境吗？
8/16
飞机的抛物线飞行第6章
宇航员的失重环境
下面两种环境等效吗？宇航员在水中训练宇航员在太空中飘游
质点动力学
任何在重力场中做自由飞行的飞行器都具有加速度g，由此产生的惯性力恰好与重力抵消，从而在其内部造成完全失重的环境
e
e
7/16
第 6章
9/16
例 6-2-2 第6章已知水平圆盘绕O轴转动，角速度 = const。
求小球相对圆盘的运动和光滑槽对小球的横向作用力。
11/16
质点动力学质点动力学质点动力学源自质点动力学r
O1
Sc
vr m
O ac
O2
r
O1
O
v r ac
Sc
O2

Fz mz
0 Fb
Fz mz
mx 0 Fd t mx
t0
t
（质点动量定理）
4/16
运动微分方程求解方法
F (t , x, x ) mx
) 时当 F F (x d x x dt m dx dt ) F (x
分离变量法第6章
地球自转的影响第 6章
牵连惯性力的影响