分析力学!2质点运动微分方程例题4
质点运动微分方程
则该一阶微分方程称为质点运动微分方程的运动
积分, 积分常数 C 由初始条件确定. 从 数学 上看 , 找 到运动积分 使 运动微分方程 由二阶微分方程降为一阶微分方程, 有利于求解. 从物理上看 , 第一积分 对 应 着某 个运动 守恒 量, 可能有明确的物理意义. 我 们常 利 用 物理意义明 确的第一积分 , 如动 量守恒、 角动量守恒和机械能守恒等, 以达到简 化问题求解过程的目的. 三、约束 牛顿力学中力的分类 1. 约束的概念和约束方程. 约束是预先给定的、 由约束物给出的对力学 系统 (目前指质点) 运动的限制. 有关约束, 读者应注意以下三点: (1) 约束是预先给定的并由约束物给出. (2) 我 们 抛 出一个质点 , 忽略空气阻 力时 , 它 必沿某 一 抛物 线运动 , 这 是由动力学 规 律和运 动初始条件 决 定的 , 质点不 受约束 , 运动是 自 由 的. (3) 约束既 包括 对 质点位置的 限制 , 又 包括 对质点速度的限制. 用数学方 法表述约束 条件的方程称为 约束 方 程. 质点受到约束, 其自由度减少. 自由质点和非自由质点.
x 2 + y 2 = l 2 z = 0
质 点 受 约 束 力 FR = FT F = W = mg .
r = l 或 z = 0
( 绳 张 力 ), 主 动 力
(2)约束方程为
y = 0 z = 0
质点受约束力 FR = FN + F f , 注意支撑力 FN 和摩擦力 F f
未知函数即为运动学方程 r = r(t). 相当于 3 个标量
的二阶微分方程,如
= Fx ( x, y, z, x , y , z m , t ) x = Fy ( x, y, z, x , y , z , t ) y m , y , z , t ) mz = Fz ( x, y, z, x
第八章质点的运动微分方程
第八章质点的运动微分方程第1节动力学的基本定律动力学基本定律(牛顿三定律)是质点动力学的基础，出自牛顿(公元1642─1727)名著《自然哲学之数学原理》，但它们只能直接应用于质点。
第一定律：(又称惯性定律)质点如不受其它物体(力)作用，则将保持静止或匀速直线运动的状态。
任何质点保持其运动状态不变的特性，称为惯性。
而质点的匀速直线运动又称为惯性运动。
第二定律：(力与加速度之间关系的定律)质点受到力作用时所获得的加速度，其大小与力的大小成正比，而与质点的质量成反比；加速度的方向与力的方向相同。
ma=F(8-1-1-1)式中a为质点的加速度，m为质点的质量，F为作用于质点上之外力。
由式(8-1-1-1)知：以同样的力作用在质点上，当质量m愈大，则加速度a愈小，质点愈不容易改变它的运动状态。
因此，质点的质量是其惯性的度量。
第三定律：(作用力与反作用力定律)两个物体相互作用的力，总是大小相等、方向相反、沿同一直线，且同时分别作用在两个物体上。
此定律既适用于平衡的物体，而且也适用于任何运动的物体。
第2节质点的运动微分方程一、质点动力学基本方程动力学基本定律中的第二定律建立了作用于质点的合力F和质点的运动状态变化（通过加速度a表示出来）以及质点的质量m三者间的定量关系，即ma＝Ｆ(8-2-1-1)它是研究质点动力学问题的基础，故称其为质点动力学基本方程。
工程实际中的大多数问题常把与地球固连的坐标系作为惯性参考系，称为静参考系。
因此，动力学基本方程(8-2-1-1)中的加速度a应为质点的绝对加速度。
二、质点运动微分方程1.矢量形式m d 2 r d t 2=F (8-2-1-2)其中r是质点对固定点Ｏ的矢径。
2.直角坐标形式图8-2-1-1 质点运动微分方程在直角坐标轴上投影将式(8-2-1-2)投影在直角坐标轴上m d 2 x d t 2 = F x m d 2 y d t 2 = F y m d 2 z d t 2 = Fz } (8-2-1-3)其中Fx、Fy、Fz是合力F在固定直角坐标系Oxyz各轴上的投影；x、y、z是质点的相应坐标。
大学物理质点运动例题
s = Rω t
r r r 例1：某质点运动方程为 r = R cos(ωt)i + R sin(ωt ) j
质点在t =0S、 1S时位置矢量 时位置矢量； 求：（1）质点在t1=0S、t2＝1S时位置矢量； 1S内的位移 内的位移； （2）在∆t=t2－t1＝1S内的位移； 1S内的平均速度 内的平均速度； （3）在∆t=t2－t1＝1S内的平均速度； 质点在t时刻的速度； （4）质点在t时刻的速度； r r r r r r2 = R cosωi + R sin ω j 解： （1）r1 = Ri
dV at = = dt
2
d
(
4t 2 +1 dt
2 t
)=
2
4t 4t 2 +1
an = a − a =
4t 2 +1
13
例题1 在河水流速 0 = 2 m/s 的地方有小船渡河，如希望 在河水流速v 的地方有小船渡河， 例题 的速率垂直于河岸横渡， 小船 以v = 4 m/s 的速率垂直于河岸横渡 ， 问小船相对于河 水的速度大小和方向应如何？ 水的速度大小和方向应如何？ 取河水的流向如图。 解 取河水的流向如图。 求的是
根据质点加速度的定义 根据质点加速度的定义
v v dv a= dt
v v 2 2v = ( −ω R cos ωt )i + ( −ω R sin ωt ) j = −ω r
2
r r r r r 2 r [例1]已知：质点加速度为 a = 12 j m / s , v 0 = 5i m / s , r0 = 7 km 已知： 例 已知 r r 求： v ( t ), r ( t ) d vx Q = 0∴ d vx = 0 求速度： 解：1、求速度： a x = dt v Q v x (0) = 5 由初条件积分 ∫ d v x = 0 ∴ v x = 5
笫二章质点动力学
F
13
四、力的分类
在目前的宇宙中，存在着四类基本的相互作用，所有的 运动现象的原因都逃不出这四类基本的力,各式各样的力只不 过是这四类基本力在不同情况下的不同表现.
四种力：万有引力，电磁力，强力和弱力
万有引力 电 磁 力
强力
弱力
适用范围 m
相互作用举 例
长程力
长程力
1015
1016
恒星结合在一 电子和原子核 质子和中子结 表征核子
起形成银河系 结合形成原子 合形成原子核 衰变的力
相对强度
1039
102
1
105
14
㈣ 牛顿运动定律应用
一、动力学的典型问题可归结为两类：
笫一类问题：己知作用于物体（质点）上的力，由力 学规律来决定该物体的运动情况或平衡状态.
笫二类问题：己知物体的运动情况或平衡状态，由 力学规律来推究作用于物体上各种力.
d 2
d 2
,
cos
d 2
1
整理以上方程可得：
dT N
1 dTd Td N
2
18
TA TB
dT T
0d
ln TA TB
TB TAe
讨论： 如果 0.25
则： 时， TB 0.46TA
2时， TB 0.21TA
10时， TB 0.00039TA
19
例题2－2 从实验知道,当物体速度不大时,可认为空 气阻力正比于物体的速度,问以初速度竖直向上运动 的物体,其速度将如何变化？
一、万有引力与重力
F
G
m1m2 r2
mr
1
m
2
重力:地球对表面物体的 万有引力mg
g
第2章《质点运动学》习题解答
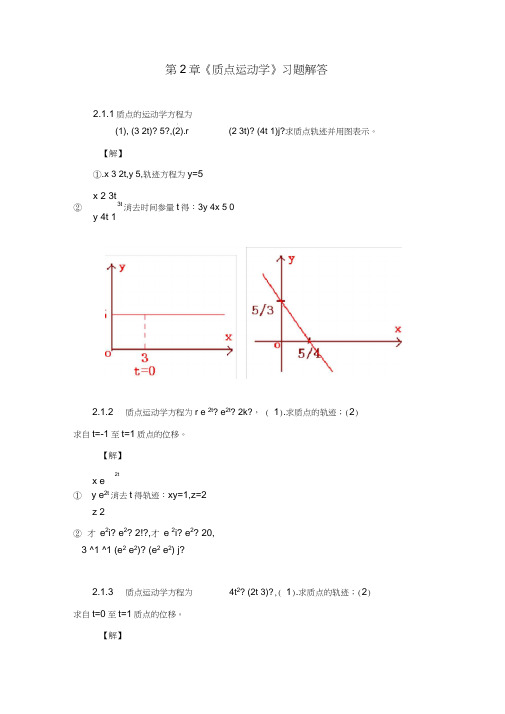
第2章《质点运动学》习题解答2.1.1质点的运动学方程为I(1), (3 2t)? 5?,(2).r(2 3t)? (4t 1)j?求质点轨迹并用图表示。
【解】①.x 3 2t,y 5,轨迹方程为y=5x 2 3t②3t消去时间参量t 得：3y 4x 5 0y 4t 12.1.2 质点运动学方程为r e 2t ? e 2t ? 2k?， ( 1).求质点的轨迹；(2)求自t=-1至t=1质点的位移。
【解】2tx e ① y e 2t 消去t 得轨迹：xy=1,z=2z 2② 才 e 2i? e 2? 2!?,才 e 2i? e 2? 20,3 ^1 ^1 (e 2 e 2)? (e 2 e 2) j?2.1.3 质点运动学方程为求自t=0至t=1质点的位移。
【解】4t 2? (2t 3)?,( 1).求质点的轨迹；(2)①.x 4t 2, y 2t 3,消去t 得轨迹方程x (y 3)2②r 0 3?』2.2.1雷达站于某瞬时测得飞机位置为R i 4100m, i 33.70，°.75s 后测得R 2 4240m, 2 29.3°, R,R 2均在铅直平面内。
求飞机瞬时速率的近似值和飞行方向（a 角）。
R i 2 R ； 2RR, cos( i 2)代入数值得: .41002 42402 -2 4100 4240cos 4.4°349.385(m)利用正弦定理可解出34.8902.2.2 一小圆柱体沿抛物线轨道运动，抛物线轨道为y x 2 / 200 （长度mm 。
第一次观察到圆柱体在349.3850.75 465.8(m/s)x=249mn 处，经过时间2ms 后圆柱体移到 x=234mn 处。
求圆柱体瞬时速度的近似4i? 5? r4? 2?t［解］19.6mm/ms152 36.22522112.502.2.3 一人在北京音乐厅内听音乐，离演奏者 17m 另一人在广州听同一 演奏的转播，广州离北京2320km 收听者离收音机2m 问谁先听到声音？声速 为340m/s,电磁波传播的速度为3.0 108m/s 。
理论力学—质点系运动微分方程
解
AB杆的动力学方程：
mxc mg TA
myc 0
1 12
ml 2
1 2
lTA
需补充方程后求解
o
y
TA
A
c
yc B
mg
x
xc
ac aA art arn
xc
art
1 2
l
aA 0; art l / 2; arn 0 ( 0)
联立求解得：
3g
在例1中，对瞬心D的动量 矩为：
JD
1 12
ml 2
1 ml2 4
1 ml2 3
保持不变
由对瞬心D的动量矩定理：
1 ml2 1 mgl sin
3
2
3g 2l
sin
y
A XA
D
C
P O
YB x
B
与前面结果相同
第7章
质 点 系 动 力 学
讨论
对瞬心的动量矩定理
J C*
3 mr 2 2
第7章
质 点 系 动 力 学
讨论
对瞬心的动量矩定理
若圆盘有偏心。
y
J A JC + m 2
随时间而变
O
dLA dt
J A
m d 2
dt
dLA dt
J A
x
C
A mg
N
F
x
仅当动瞬心到质心的距离保持不变时才有：
dLA dt
J A
讨论
对瞬心的动量矩定理
质点的运动微分方程例题
质点的运动微分方程例题当涉及到质点的运动微分方程时，我们通常考虑质点在空间中的位置、速度和加速度之间的关系。
下面我将给出一个质点的运动微分方程的例题，并从多个角度进行回答。
例题，一个质点在直角坐标系中的运动满足以下条件，质点的位置矢量为r(t) = (3t^2, 2t, t^3)，其中t为时间，求质点的速度和加速度。
从向量的角度回答：质点的速度可以通过对位置矢量求导得到。
对r(t) = (3t^2, 2t, t^3)关于时间t求导，得到速度矢量v(t) = (6t, 2, 3t^2)。
质点的加速度可以通过对速度矢量求导得到。
对v(t) = (6t, 2, 3t^2)关于时间t求导，得到加速度矢量a(t) = (6, 0, 6t)。
从微分方程的角度回答：质点的速度可以表示为位置矢量对时间的导数，即v(t) =dr(t)/dt。
根据给定的位置矢量r(t) = (3t^2, 2t, t^3)，对其分别对时间求导，得到速度矢量v(t) = (6t, 2, 3t^2)。
质点的加速度可以表示为速度矢量对时间的导数，即a(t) = dv(t)/dt。
根据给定的速度矢量v(t) = (6t, 2, 3t^2)，对其分别对时间求导，得到加速度矢量a(t) = (6, 0, 6t)。
从运动学的角度回答：根据质点的位置矢量r(t) = (3t^2, 2t, t^3)，我们可以计算质点在各个方向上的速度和加速度。
在x方向上，质点的速度v_x(t) = d(3t^2)/dt = 6t，加速度a_x(t) = d(6t)/dt = 6。
在y方向上，质点的速度v_y(t) = d(2t)/dt = 2，加速度a_y(t) = d(2)/dt = 0。
在z方向上，质点的速度v_z(t) = d(t^3)/dt = 3t^2，加速度a_z(t) = d(3t^2)/dt = 6t。
从微分方程的角度回答：根据位置矢量r(t) = (3t^2, 2t, t^3)，我们可以得到速度矢量v(t) = (6t, 2, 3t^2)和加速度矢量a(t) = (6, 0, 6t)。
分析力学第四章
m ( && − r θ& 2 ) = ∑ F ir r & & m ( r θ& + 2 r θ& ) = ∑ F i θ
& & 个积分常数: 有4个积分常数 ( r0 , θ 0 , r0 , θ 0 ) 个积分常数
说明平面自由质点某时刻的力学状态需 2×2 个量描述 × 个量描述.
法平面
主法线 密切平面
v R
r n
次法线
r b
直切平面
质点在密切面内运动， 质点在密切面内运动， 与法平面相互垂直
切线
τ
r
解题步骤: 解题步骤
① ② ③ ④
隔离物体 具体分析 选定坐标 运动方程
加速度
理论力学的主要任务:物理问题 理论力学的主要任务 物理问题
数学问题, 数学问题 求解 确定结果的物理意义
(6) 匀变速直线运动
v = v0 + aτ t
v = v + 2 aτ ( s − s0 )
2 2 0
s = s0 + v0 t + aτ t
1 2
2
适用条件为: 常量， 适用条件为: α τ =常量， an = 0.
二、平动参照系: (§1.3) 平动参照系 § 静系: 静系 S 动系: S’ 动系 (可以认为是刚 可以认为是刚 可以认为是 的平动) 体的平动 位矢
径向 横向
（4） 自然坐标 ）
利用质点运动轨道本身的几何特性 (如切线、 如切线、 法线方向等)来描述质点的运动. 法线方向等)来描述质点的运动. 这种方法称为自 然坐标法. 然坐标法.
1. 弧长方程
在轨道上取一点 O 作原点, 规定沿轨道的某一 作原点, 方向为弧长的正方向, 方向为弧长的正方向, 质点位置可由原点 O 到质点 来确定, 称为弧坐标. 间的一段弧长 s 来确定, s 称为弧坐标.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2） 约束力和主动力
约束是通过约束物实现的, 为强制质点满足约束 条件, 约束物与质点间有力的相互作用, 称约束物 对质点施加的力为约束力 (或称为约束反力, 约束 反作用力).而把质点所受的, 除约束力之外的其他 力称为主动力 (叫非约束力可能更准确).
§3-2 质点运动微分方程
lm。0.05
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
§3-2 质点运动微分方程
y
( mv0 y b
m2g b2
)(1
e
b m
t
)
mg b
t
§3-2 质点运动微分方程
讨论 （1） t 时,
v, x 0
vy
mg b
,
x mv0x , y (实际以落地为止). b
（2）轨道方程
y (v0y
mg
m2g )x ln(1
bx
)
v0x bv0x
b0
更加深入的讨论
y v0y x 1 g x2
v0x
2 v02x
2
中世纪抛体图
对吗？ 1 3
§3-2 质点运动微分方程 对称性原理
平面运动
能量分析：水平能量耗尽，竖直运动受力平衡， 达到终极速度。
m
dv
F
dt
vdt
m
dv
F
dr
dt
d(
1 2
mv2
)
F
dr
主动力已知力的函F数
F(r, r,,t约) 束力是未知的.
弹性力：弹簧弹性力、绳的张力、面的支撑力
（3） 在牛顿第二定律中主动力和约束力的地位是
平等的
mr
F(r,
r, t
)
FR
例题1 (1) 约束方程
x2 y 2 l 2 r l
z 0
m dvx dt
Fx
vx
dt
m
dvx dt
Fxdx
d(
1 2
mv
2 x
)
Fxdx
§3-2 质点运动微分方程
三种情况下的动力学微分方程
伽里略无阻力模型
mx 0
F
bv
my mg mx bx
F
bvv
my mg by mx b x2 y2 x
mr
mv
mg
bv
即
mvx bvx mvy mg bvy
§3-2 质点运动微分方程
mvx bvx
x
mv 0 x
bt
(1 ex v0xe m
vy
(v0 y
mg b
bt
)e m
mg b
mz Fz (x, y, z, x, y, z,t)
§3-2 质点运动微分方程 线性:力是位置和速度的线性函数，有一般的 解法，线性方程只是实际问题中的少数情况.
非线性:力是位置和速度的非线性函数，无一 般的解法，实际问题中大多数是非线性的.
如它果们能由求初条出解件析t 解时,0其通解r和中r应0 有确6定v个 .积v分0 常数,
mr
F (r ,
r, t )
例题2 实验表明，阻力与速率一次方成正比的规律仅 适用于速度量级为10-2m/s的极其缓慢运动。一般情 况下，阻力与速率平方成正比的规律较符合实际情况。 但此时方程是非线性的，求解析解很复杂。采用简单 的情况进行讨论，虽然不完全符合实际，但仍能了解 有阻力情况下抛体运动的一些共同特征。
my mg b x2 y2 y
§3-2 质点运动微分方程
F bv2 情况下终极速度的估算
设物体尺度为 l
F mg
bvz2 mg
l 2vz2 l 3
vz l
人
vz m5/0s
伞
vz m6/s
人 l 1m.8，小鸟（鼠）
可解释 很多现 象！！！
根据问题的特点选用不同的坐标系很重要！
§3-2 质点运动微分方程
2. 质点运动微分方程的运动积分(初积分或第 一积分) 将运动微分方程G作(一r,次r,积t) 分 ,C得到一阶微分方程
该一阶微分方程称为质点运动微分方程的运动积分,
积分常数 C由初始条件确定.
从数学上看, 找到运动积分使运动微分方程由二 阶微分方程降为一阶微分方程, 有利于求解.
§3-2 质点运动微分方程
1. 质点运动微分方程
力 F的函数中不包括其他质点的位置和速度
F
F(r,
r, t)
质点的运动微分方程
mr F(r, r,t)
r r(t)
mx my
Fx Fy
(x, (x,
y, y,
z, z,
x, y, z,t) x, y, z,t)
非线性微分方程组无一般解法，通常采用计算机求数
值解，为一般化，我们考虑 F 模v型n
mx
b( x2
y )2
n1 2
x
my
mg
b( x2
b2
mv0 x
§3-2 质点运动微分方程
与无阻力情况轨道比较
b0
泰勒展开
ln(1 bx ) bx
mv 0 x
mv 0 x
1 ( bx )2 1 ( bx )3 2 mv0x 3 mv0x
y
v0 y v0 x
x
1 2
g v02x
x2
1 3
bx mv30 x
x3
§3-2 质点运动微分方程 这回可以了！！！
或
z 0
约束力 主动力
FR FT
F W mg
§3-2 质点运动微分方程
(2) 约束方程
y 0
z 0
约束力 FR FN Ff
主动力
F W F1 mg kxi
空气阻力也是主动力
§3-2 质点运动微分方程
4. 自由质点的动力学方程组及例题
从物理上看, 第一积分对应着某个运动守恒量, 可能有明确的物理意义.
我们常利用物理意义明确的第一积分, 如动量守 恒、角动量守恒和机械能守恒等, 以达到简化问题求 解过程的目的.
§3-2 质点运动微分方程
3. 约束 牛顿力学中力的分类
（1） 约束的概念和约束方程
约束是预先给定的、由约束物给出的对力学系统 运动的限制.