2018届高考数学(文)大一轮复习检测第三章第2讲同角三角函数的基本关系与诱导公式Word版含答案
2018届高考数学(文)大一轮复习教师用书第3章三角函数、解三角形第2节同角三角函数的基本关系与诱导公式Wo
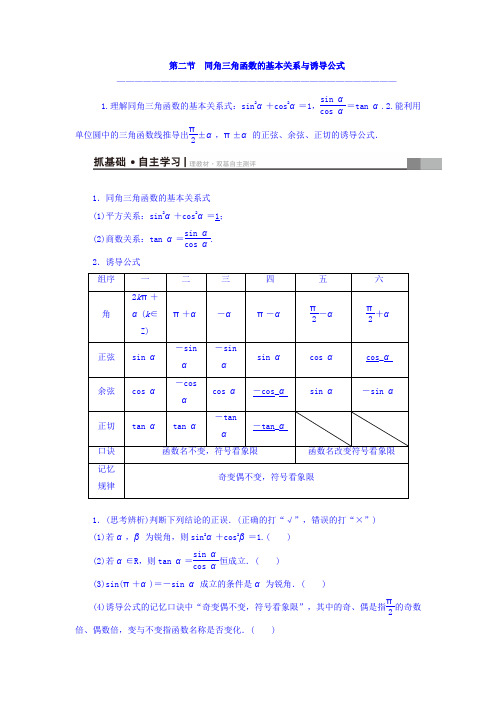
第二节 同角三角函数的基本关系与诱导公式———————————————————————————————— 1.理解同角三角函数的基本关系式:sin 2α+cos 2α=1,sin αcos α=tan α.2.能利用单位圆中的三角函数线推导出π2±α,π±α的正弦、余弦、正切的诱导公式.1.同角三角函数的基本关系式 (1)平方关系:sin 2α+cos 2α=1; (2)商数关系:tan α=sin αcos α.2.诱导公式1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( ) (2)若α∈R ,则tan α=sin αcos α恒成立.( )(3)sin(π+α)=-sin α成立的条件是α为锐角.( )(4)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍、偶数倍,变与不变指函数名称是否变化.( )(1)× (2)× (3)× (4)√2.(教材改编)已知α是第二象限角,sin α=513,则cos α等于( )A .-513B .-1213C.513D.1213B3.(2017·陕西质检(二))若tan α=12,则sin 4α-cos 4α的值为( )A .-15B .-35C.15D.35B4.(2016·四川高考)sin 750°=________. 125.已知sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝⎛⎭⎪⎫0,π2,则sin(π+α)=________.【导学号:31222107】-45(1)已知sin αcos α=18,且5π4<α<3π2,则cos α-sin α的值为( )A .-32B.32C .-34D.34(2)(2016·全国卷Ⅲ)若tan α=34,则cos 2α+2sin 2α=( )A.6425B.4825 C .1 D.1625(1)B (2)A1.利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.2.应用公式时要注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.3.注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.已知sin α-cos α=2,α∈(0,π),则tan α等于( ) A .-1 B .-22C.22D .1A(1)已知A =sin α+cos α(k ∈Z),则A 的值构成的集合是( )A .{1,-1,2,-2}B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}(2)已知tan ⎝ ⎛⎭⎪⎫π6-α=33,则tan ⎝ ⎛⎭⎪⎫5π6+α=________.(1)C (2)-331.利用诱导公式应注意已知角或函数名称与所求角或函数名称之间存在的关系,尤其是角之间的互余、互补关系,选择恰当的公式,向所求角和三角函数进行化归.2.诱导公式的应用原则:负化正、大化小、小化锐、锐求值. 已知cos ⎝ ⎛⎭⎪⎫π6-α=33,则cos ⎝ ⎛⎭⎪⎫5π6+α-sin 2⎝ ⎛⎭⎪⎫α-π6的值为________.-2+33(1)(2016·全国卷Ⅰ)已知θ是第四象限角,且sin ⎝ ⎛⎭⎪⎫θ+4=5,则tan ⎝ ⎛⎭⎪⎫θ-4=________.(2)(2017·郑州质检)已知cos ⎝ ⎛⎭⎪⎫π2+α=2sin ⎝⎛⎭⎪⎫α-π2,则sin3π-α+α+π5cos ⎝ ⎛⎭⎪⎫5π2-α+3sin ⎝ ⎛⎭⎪⎫7π2-α的值为________.(1)-43 (2)335利用同角三角函数基本关系式和诱导公式化简三角函数的基本思路和化简要求:(1)基本思路:①分析结构特点,选择恰当公式;②利用公式化成单角三角函数;③整理得最简形式.(2)化简要求:①化简过程是恒等变形;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.(2016·安徽皖南八校联考)已知sin α=13,α是第二象限角,则tan(π-α)=________.24三角函数求值与化简的常用方法(1)弦切互化法:主要利用公式tan α=sin αcos α进行弦、切互化.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4等.(4)利用相关角的互补、互余等特殊关系可简化解题步骤.1.利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.应特别注意函数名称和符号的确定.2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.课时分层训练(十八)同角三角函数的基本关系与诱导公式A 组 基础达标 (建议用时:30分钟)一、选择题1.若cos α=13,α∈⎝ ⎛⎭⎪⎫-π2,0,则tan α等于( ) 【导学号:31222109】A .-24B.24C .-2 2D .2 2C2.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6B .-π3C.π6D.π3D 3.cos 350°-2sin 160°-=( )A .- 3B .-32C.32D. 3D4.(2016·山东实验中学二诊)已知sin θ+cos θ=43⎝ ⎛⎭⎪⎫0<θ<π4,则sin θ-cos θ的值为( )A.23B .-23C.13 D .-13B5.(2016·浙江杭州五校联盟高三一诊)已知倾斜角为θ的直线与直线x -3y +1=0垂直,则23sin 2θ-cos 2θ=( ) A.103 B .-103C.1013D .-1013C 二、填空题6.若sin ⎝ ⎛⎭⎪⎫π6-α=13,则cos ⎝ ⎛⎭⎪⎫π3+α=________. 【导学号:31222110】137.已知α是三角形的内角,且sin α+cos α=15,则tan α=________.-438.已知α为第二象限角,则cos α1+tan 2α+sin α·1+1tan 2α=________. 【导学号:31222111】0 三、解答题9.求值:sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 945°.原式=-sin 1 200°·cos 1 290°+cos 1 020°·(-sin 1 050°)+tan 945°3分=-sin 120°·cos 210°+cos 300°·(-sin 330°)+tan 225°6分 =(-sin 60°)·(-cos 30°)+cos 60°·sin 30°+tan 45°9分 =⎝ ⎛⎭⎪⎫-32×⎝ ⎛⎭⎪⎫-32+12×12+1=2.12分 10.已知sin(3π+α)=2sin ⎝ ⎛⎭⎪⎫3π2+α,求下列各式的值:(1)sin α-4cos α5sin α+2cos α; (2)sin 2α+sin 2α.由已知得sin α=2cos α.2分 (1)原式=2cos α-4cos α5×2cos α+2cos α=-16.7分(2)原式=sin 2α+2sin αcos αsin 2α+cos 2α =sin 2α+sin 2αsin 2α+14sin 2α=85.12分B 组 能力提升 (建议用时:15分钟)1.已知tan x =sin ⎝⎛⎭⎪⎫x +π2,则sin x =( )A.-1±52 B.3+12 C.5-12D.3-12C2.sin 21°+sin 22°+sin 23°+…+sin 289°=________.【导学号:31222112】44.53.已知f (α)=π-απ-α⎝ ⎛⎭⎪⎫-α+3π2tan ⎝ ⎛⎭⎪⎫π2+α-π-α.(1)化简 f (α);(2)若α是第三象限角,且cos ⎝⎛⎭⎪⎫α-3π2=15,求f (α)的值.(1)f (α)=sin α·cos α·tan ⎝ ⎛⎭⎪⎫-α+3π2-2πtan ⎝ ⎛⎭⎪⎫π2+α·sin α=sin α·cos α·⎣⎢⎡⎦⎥⎤-tan ⎝ ⎛⎭⎪⎫π2+αtan ⎝ ⎛⎭⎪⎫π2+α·sin α=-cos α.5分(2)∵cos ⎝ ⎛⎭⎪⎫α-3π2=-sin α=15, ∴sin α=-15,7分又α是第三象限角,∴cos α=-1-sin 2α=-265,故f (α)=265.12分。
2018届高考数学一轮复习 第三章 三角函数、解三角形 第二节 同角三角函数的基本关系式与诱导公式学

第二节 同角三角函数的基本关系式与诱导公式1.理解同角三角函数的基本关系式:sin 2α+cos 2α=1,sin αcos α=tan α.2.能利用单位圆中的三角函数线推导出π2±α,π±α的正弦、余弦、正切的诱导公式.知识点一 同角三角函数基本关系式1.平方关系:sin 2α+cos 2α=1,其等价形式为:sin 2α=1-cos 2α,cos 2α=________. 2.商数关系:__________,其等价形式为:sin α=____________,cos α=sin αtan α. 答案1.1-sin 2α 2.sin αcos α=tan α cos αtan α1.已知cos α=1213,且α是第四象限角,则sin α的值为________.解析:由于α是第四象限角,故sin α=-1-cos 2α=-513.答案:-5132.已知sin α-2cos α3sin α+5cos α=-5,那么tan α的值为________.解析:由sin α-2cos α3sin α+5cos α=-5,知cos α≠0,分子分母同时除以cos α可得tan α-23tan α+5=-5,解得tan α=-2316.- 2 -答案:-23163.(2016·新课标全国卷Ⅲ)若tan α=34,则cos 2α+2sin 2α=( )A .6425B .4825C .1D.1625解析:通性通法:由tan α=sin αcos α=34,cos 2α+sin 2α=1,得⎩⎪⎨⎪⎧sin α=35cos α=45或⎩⎪⎨⎪⎧sin α=-35,cos α=-45,则sin 2α=2sin αcos α=2425,则cos 2α+2sin 2α=1625+4825=6425.光速解法:cos 2α+2sin 2α=cos 2α+4sin αcos αcos 2α+sin 2α=1+4tan α1+tan 2α=1+31+916=6425. 答案:A知识点二 六组诱导公式-sin α cos α cos α -sin α -tan α4.计算sin 10π3-2cos ⎝ ⎛⎭⎪⎫-19π4+tan ⎝ ⎛⎭⎪⎫-13π3=________.解析:原式=sin ⎝ ⎛⎭⎪⎫2π+4π3-2cos ⎝ ⎛⎭⎪⎫4π+3π4-tan ⎝ ⎛⎭⎪⎫4π+π3=sin ⎝ ⎛⎭⎪⎫π+π3-2cos ⎝⎛⎭⎪⎫π-π4-tan π3=-sin π3+2cos π4-3=-332+1.答案:-332+15.已知tan α=3,π<α<32π,则cos α-sin α=________.解析:∵tan α=3,π<α<32π,∴α=43π,∴cos α-sin α=cos 43π-sin 43π=-cosπ3+sin π3=-12+32=3-12.答案:3-12热点一 同角三角函数基本关系式的应用 考向1 运用公式直接求值 【例1】 (1)若sin α=-513,且α为第四象限角,则tan α的值等于( ) A.125 B .-125C.512D .-512(2)sin 21°+sin 22°+…+sin 289°=________. 【解析】 (1)因为α为第四象限的角, 故cos α=1-sin 2α=1-⎝ ⎛⎭⎪⎫-5132=1213, 所以tan α=sin αcos α=-5131213=-512.选D.(2)原式=(sin 21°+sin 289°)+(sin 22°+sin 288°)+…+(sin 244°+sin 246°)+sin 245°=(sin 21°+cos 21°)+(sin 22°+cos 22°)+…+(sin 244°+cos 244°)+12=1+1+1+ (144)+12=4412.故填4412.- 4 -【答案】 (1)D (2)4412考向2 关于sin α,cos α的齐次式问题【例2】 若tan α=-43,则sin α-4cos α5sin α+2cos α=________,sin 2α+2sin αcos α=________.【解析】sin α-4cos α5sin α+2cos α=tan α-45tan α+2=-43-45×⎝ ⎛⎭⎪⎫-43+2=87.sin 2α+2sin αcos α=sin 2α+2sin αcos αsin 2α+cos 2α=tan 2α+2tan α1+tan 2α=169-831+169=-825. 【答案】 87 -825(1)已知cos α=k ,k ∈R ,α∈⎝ ⎛⎭⎪⎫π2,π,则sin(π+α)=( )A .-1-k 2B.1-k 2C .±1-k 2D .-k(2)已知sin α+2cos α=3,则tan α=( )A.22 B. 2C .-22D .- 2解析:(1)由cos α=k ,α∈⎝ ⎛⎭⎪⎫π2,π,得sin α=1-k 2,所以sin(π+α)=-sin α=-1-k 2,故选A.(2)因为sin α+2cos α=3, 所以(sin α+2cos α)2=3.所以sin 2α+22sin αcos α+2cos 2α=3. 所以sin 2α+22sin αcos α+2cos 2αsin 2α+cos 2α=3. 所以tan 2α+22tan α+2tan 2α+1=3. 所以2tan 2α-22tan α+1=0.所以tan α=22. 答案:(1)A (2)A 热点二 诱导公式的应用 考向1 利用诱导公式求值 【例3】 (1)已知sin ⎝ ⎛⎭⎪⎫5π2+α=15,那么cos α=( ) A .-25B .-15C.15D.25(2)已知A =k π+αsin α+k π+αcos α(k ∈Z ),则A 的值构成的集合是( ) A .{1,-1,2,-2} B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}【解析】 (1)sin ⎝⎛⎭⎪⎫5π2+α=sin ⎝ ⎛⎭⎪⎫π2+α=cos α=15.(2)当k 为偶数时,A =sin αsin α+cos αcos α=2;k 为奇数时,A =-sin αsin α-cos αcos α=-2. 【答案】 (1)C (2)C 考向2 巧用“角”间关系求值- 6 -【例4】 (1)已知sin ⎝ ⎛⎭⎪⎫π3-α=12,则cos ⎝ ⎛⎭⎪⎫π6+α=________.(2)已知tan ⎝ ⎛⎭⎪⎫π6-α=33,则tan ⎝ ⎛⎭⎪⎫56π+α=________.【解析】 (1)∵⎝ ⎛⎭⎪⎫π3-α+⎝ ⎛⎭⎪⎫π6+α=π2,∴cos ⎝ ⎛⎭⎪⎫π6+α=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π3-α=sin ⎝ ⎛⎭⎪⎫π3-α=12.(2)∵⎝ ⎛⎭⎪⎫π6-α+⎝ ⎛⎭⎪⎫5π6+α=π, ∴tan ⎝ ⎛⎭⎪⎫56π+α=-tan ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫56π+α =-tan ⎝ ⎛⎭⎪⎫π6-α=-33.【答案】 (1)12 (2)-33(1)计算:π+απ+α⎝ ⎛⎭⎪⎫α-3π2-α-3π-3π-α=________.(2)已知cos ⎝ ⎛⎭⎪⎫π6+α=33,则cos ⎝ ⎛⎭⎪⎫5π6-α的值为________.解析:(1)原式=tan αcos αcos α-cos αsin α=-1.(2)cos ⎝⎛⎭⎪⎫5π6-α=cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6+α=-cos ⎝ ⎛⎭⎪⎫π6+α=-33,即cos ⎝ ⎛⎭⎪⎫5π6-α=-33.答案:(1)-1 (2)-33热点三 sin α±cos α与sin αcos α的关系【例5】 已知α是三角形的内角,且sin α+cos α=15.(1)求tan α的值;(2)把1cos 2α-sin 2α用tan α表示出来,并求其值. 【解】 (1)解法1:联立方程 ⎩⎪⎨⎪⎧sin α+cos α=15, ①sin 2α+cos 2α=1, ②由①得cos α=15-sin α,将其代入②,整理得25sin 2α-5sin α-12=0. ∵α是三角形内角, ∴⎩⎪⎨⎪⎧sin α=45,cos α=-35,∴tan α=-43.解法2:∵sin α+cos α=15,∴(sin α+cos α)2=⎝ ⎛⎭⎪⎫152,即1+2sin αcos α=125,∴2sin αcos α=-2425,∴(sin α-cos α)2=1-2sin αcos α=1+2425=4925.∵sin αcos α=-1225<0且0<α<π,∴sin α>0,cos α<0,sin α-cos α>0. ∴sin α-cos α=75.- 8 -由⎩⎪⎨⎪⎧sin α+cos α=15,sin α-cos α=75,得⎩⎪⎨⎪⎧sin α=45,cos α=-35,∴tan α=-43.(2)1cos 2α-sin 2α=sin 2α+cos 2αcos 2α-sin 2α =sin 2α+cos 2αcos 2αcos 2α-sin 2αcos 2α=tan 2α+11-tan 2α. ∵tan α=-43,∴1cos 2α-sin 2α=tan 2α+11-tan 2α=⎝ ⎛⎭⎪⎫-432+11-⎝ ⎛⎭⎪⎫-432=-257.求解此类问题的关键是:通过平方关系,对称式sin α+cos α,sin α-cos α,sin αcos αt 2-1已知-π2<x <0,sin x +cos x =15,则sin x -cos x =____.解析:将等式sin x +cos x =15两边平方,得sin 2x +2sin x ·cos x +cos 2x =125,即2sin x cos x=-2425,∴(sin x -cos x )2=1-2sin x cos x =4925.又-π2<x <0,∴sin x <0,cos x >0,sin x -cos x <0,故sin x -cos x =-75.答案:-75“a sin θ+b cos θ=m ”型化简、求值方法已知a sin θ+b cos θ=m (其中a ,b ,m 为常数),求sin θ,cos θ,tan θ等值时,有如下思路:(1)若a =1,b =±1,则利用以下三个关系式:(sin θ+cos θ)2=1+2sin θcos θ,(sin θ-cos θ)2=1-2sin θcos θ,(sin θ+cos θ)2+(sin θ-cos θ)2=2,可得a sin θ-b cos θ的值,然后解方程组得结论.(2)直接解方程组⎩⎪⎨⎪⎧a sin θ+b cos θ=m ,sin 2θ+cos 2θ=1,得结论.(3)构造“对偶式”b sin θ-a cos θ=x ,两式平方并相加求得x ,然后解方程组得结论. (4)把等式平方,逆用cos 2θ+sin 2θ=1,化为cos θ,sin θ的齐次式,利用“弦化切”,得tan θ,再求sin θ,cos θ.【例】 已知3sin α+4cos α=5,求tan α.【解】 解法1:由题意得3sin α=5-4cos α,两边平方,得9sin 2α=25-40cos α+16cos 2α,则25cos 2α-40cos α+16=0,解得cos α=45,则sin α=35,故tan α=34.解法2:把等式两边平方,整理得9sin 2α+24sin αcos α+16cos 2α=25(sin 2α+cos 2α),两边同时除以cos 2α,整理得16tan 2α-24tan α+9=0,解得tan α=34.解法3:设4sin α-3cos α=x ,则x 2+25=(4sin α-3cos α)2+(3sin α+4cos α)2=25,从而有x =0,则tan α=34.解法4:因为3sin α+4cos α=5sin(α+φ),其中cos φ=35,sin φ=45,所以sin(α+φ)=1,则α+φ=2k π+π2(k ∈Z ),则sin α=sin ⎝ ⎛⎭⎪⎫2k π+π2-φ=cos φ=35,cos α=- 10 -cos ⎝ ⎛⎭⎪⎫2k π+π2-φ=sin φ=45,故tan α=34.。
2018年高三数学(文)一轮复习课件 同角三角函数的基本关系及诱导公式

4.2
同角三角函数的基本关系及诱导公式
知识梳理 核心考点
-12-
∵α 是三角形内角, ∴
4 sin������ = 5 , ∴tan 3 cos������ = - 5 ,
α=- .
tan2 ������+1 . 1-tan2 ������
4 3
1 (2) 2 cos ������-sin2 ������
思考同角三角函数基本关系式有哪些用途?
解 (1)联立方程
1 sin������ + cos������ = , 5
sin2 ������ + cos2 ������ = 1.② 由①得 cos α=5-sin α,将其代入②, 整理得 25sin2α-5sin α-12=0.
1
①
第四章
考点1 考点2 考点3
=
2 4 tan2 ������+1 -3 +1 25 = =- 7 . 1-tan2 ������ 4 2 1- -3
4
5
5.(教材习题改编P22T3)已知tan θ=2,则sin θcos θ=
.
关闭
sin 2 θcos θ=
5
sin������· cos������ sin2 ������+cos2 ������
=
tan������ tan2 ������+1
=
2 22 +1
= .
解析
2 5
关闭
答案
第四章
知识梳理 双基自测 自测点评
第四章
考点1 考点2 考点3
4.2
同角三角函数的基本关系及诱导公式
知识梳理 核心考点
-11-
高考数学一轮复习第三章第二讲同角三角函数的基本关系与诱导公式课件

所以 sin α=2 5 5,cos α=- 55,tan α=-2,
所以 sin (2α-3π)+tan π2-α=-2sin αcos α+tan1 α=
-2×2
5
5×-
55-12=45-12=130.故选
D.
答案:D
2.(考向 2)已知 sinα-1π2=13,则 cosα+1172π的值为(
3sin2θ-cos2θ+( 3-1)sinθcos sin2θ+cos2θ
θ=
3tan2θ-ta1n+2θ1)=2
3+1 5.
故选 B.
答案:B
⊙sin x+cos x,sin x-cos x,sin x cos x 之间的关系 [例 4]已知 sin θ+cos θ=173,θ∈(0,π),则 tan θ 的值为_______.
(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1- cos2α,cos2α=1-sin2α.
考点二 诱导公式及其应用 考向 1 利用诱导公式化简三角函数式 [例 1](1)化简:sinc-osαπ2--32απcsoins π232+π-ααsitnan(2π(+2πα-) α)=________.
2.三角函数的诱导公式
序号
一
二
三
四
五六
角 2kπ+α(k∈Z) π+α
正弦 sin α
-sin α
-α -sin α
π-α sin α
π2-α π2+α cos α cos α
余弦 cos α
-cos α cos α -cos α sin α -sin α
正切 口诀
tan α
tan α -tan α -tan α — —
2018-2019高三数学(文)(北师大版)一轮复习课件:第3章-第2课时 同角三角函数的基本关系及诱导公式
教材梳理 基础自测 考点突破 题型透析
素能提升 应考展示 课时训练 规范解答
首页
上页 下页
尾页
考点突破 题型透析
考点一 同角三角函数的基本关系
法一:因为 sin α-cos α= 2,所以 1-2sin αcos α=2,即 sin 2α=-1, 3π 又 α∈(0,π), 所以 α= 4 ,所以 tan α=-1. 法二:将等式 sin α-cos α= 2两边平方, 得到 2sin αcos α=-1, 整理得 1+2sin αcos α=0⇒sin2α+cos2α+2sin αcos α=0⇒(sin α+cos α)2 =0⇒sin α+cos α=0, 2 2 由 sin α-cos α= 2和 sin α+cos α=0,解得 sin α= 2 ,cos α=- 2 , sin α 故 tan α=cos α=-1.
高三总复习.新课标数学(文)
第三章 第2课时
三角函数、解三角形
同角三角函数的基本关系及诱导公式
考 点
考点一 同角三角函数的基本关系 考点二 诱导公式的应用
考点三 三角函数式的化简与证明 ■易错警示•系列 ■指点迷津•展示
考纲·点击
sin α 1 .理解同角三角函数的基本关系式: sin2 α + cos2α = 1 , cos α = tan
3
教材梳理 基础自测 考点突破 题型透析
素能提升 应考展示 课时训练 规范解答
首页
上页 下页
尾页
考点突破 题型透析
考点一 同角三角函数的基本关系
审题视点
已知 sin α-cos α= 2,α∈(0,π),则 tan α=( A.-1 2 C. 2 2 B.- 2 D.1
高考一轮复习第3章三角函数解三角形第2讲同角三角函数的基本关系式与诱导公式

第二讲 同角三角函数的基本关系式与诱导公式知识梳理·双基自测 知识梳理知识点一 同角三角函数的基本关系式 (1)平方关系: sin 2x +cos 2x =1 . (2)商数关系: sin xcos x =tan x .知识点二 三角函数的诱导公式重要结论1.同角三角函数基本关系式的变形应用:如sin x =tan x·cos x,tan 2x +1=1cos 2x,(sinx +cos x)2=1+2sin xcos x 等.2.诱导公式的记忆口诀“奇变偶不变,符号看象限”.“奇”与“偶”指的是诱导公式k·π2+α(k∈Z)中的整数k 是奇数还是偶数.“变”与“不变”是指函数的名称的变化,若k 是奇数,则正、余弦互变;若k 为偶数,则函数名称不变.“符号看象限”指的是在k·π2+α(k∈Z)中,将α看成锐角时k·π2+α(k∈Z)所在的象限.双基自测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( × )(2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)sin (π+α)=-sin α成立的条件是α为锐角.( × ) (4)若sin (kπ-α)=13(k ∈Z),则sin α=13.( × )[解析] (1)根据同角三角函数的基本关系式知当α,β为同角时才正确.(2)cos α≠0时才成立.(3)根据诱导公式知α为任意角.(4)当k 为奇数和偶数时,sin α的值不同.题组二 走进教材2.(必修4P 22B 组T3改编)已知tan α=12,则sin α-cos α3sin α+2cos α=( A )A .-17B .17C .-7D .7[解析] sin α-cos α3sin α+2cos α=tan α-13tan α+2=12-13×12+2=-17.故选A.3.(必修4P 22B 组T2改编)化简cos α1-sin α1+sin α+sin α1-co s α1+cos α⎝⎛⎭⎪⎫π<α<3π2得( A )A .sin α+cos α-2B .2-sin α-cos αC .sin α-cos αD .cos α-sin α[解析] 原式=cos α1-sin α2cos 2α+sin α1-cos α2sin 2α,∵π<α<32π,∴cos α<0,sin α<0.∴原式=-(1-sin α)-(1-cos α)=sin α+cos α-2.4.(必修4P 29B 组T2改编)若sin(π+α)=-12,则sin(7π-α)= 12 ,cos ⎝ ⎛⎭⎪⎫α+3π2= 12 . [解析] 由sin(π+α)=-12,得sin α=12,则sin(7π-α)=sin(π-α)=sin α=12,cos ⎝ ⎛⎭⎪⎫α+3π2=cos ⎝ ⎛⎭⎪⎫α+3π2-2π=cos ⎝ ⎛⎭⎪⎫α-π2 =cos ⎝ ⎛⎭⎪⎫π2-α=sin α=12.题组三 走向高考5.(2019·全国卷Ⅰ)tan 255°=( D )A .-2- 3B .-2+ 3C .2- 3D .2+ 3[解析] 由正切函数的周期性可知,tan 255°=tan(180°+75°)=tan 75°=tan(30°+45°)=33+11-33=2+3,故选D.另:tan 225°=tan 75°>tan 60°=3,∴选D.6.(2015·福建)若sin α=-513,且α为第四象限角,则tan α的值等于( D )A.125B .-125C .512D .-512[解析] 因为sin α=-513,且α为第四象限角,所以cos α=1213,所以tan α=-512,故选D.7.(2017·全国卷Ⅲ)已知sin α-cos α=43,则sin 2α=( A )A .-79B .-29C .29D .79[解析] 将sin α-cos α=43的两边进行平方,得sin 2α-2sin αcos α+cos 2α=169,即sin 2α=-79,故选A.考点突破·互动探究考点一 同角三角函数的基本关系式——师生共研 例1 (1)已知α为第三象限角,cos α=-817,则tan α=( D )A .-815B .815C .-158D .158(2)已知α是三角形的内角,且tan α=-13,则sin α+cos α的值为 -5 .(3)若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 -3 .[解析] (1)因为α是第三象限角,cos α=-817,所以sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫-8172=-1517,故tan α=sin αcos α=158.选D.(2)由tan α=-13,得sin α=-13cos α,将其代入sin 2α+cos 2α=1,得109cos 2α=1,所以cos 2α=910,易知cos α<0,所以cos α=-31010,sin α=1010,故sin α+cos α=-105. (3)由角α的终边落在第三象限, 得sin α<0,cos α<0,故原式=cos α|cos α|+2sin α|sin α|=cos α-c os α+2sin α-sin α=-1-2=-3.名师点拨(1)已知一个角的三角函数值求这个角的其他三角函数值时,主要是利用公式sin 2α+cos 2α=1,tan α=sin αcos α求解,解题时,要注意角所在的象限.并由此确定根号前的正、负号,若不能确定角所在象限要分类讨论.(2)遇sin α,cos α的齐次式常“弦化切”,如:asin α+bcos αcsin α+dcos α=atan α+b ctan α+d ;sin αcos α=sin αcos α1=sin αcos αsin 2α+cos 2α=tan α1+tan 2α; sin 2α+sin αcos α-2cos 2α=sin 2α+sin αcos α-2cos 2αsin 2α+cos 2α=tan 2α+tan α-21+tan 2α. 〔变式训练1〕(1)若α是第二象限角,tan α=-512,则sin α=( C )A.15 B .-15C .513D .-513(2)已知α是第二象限角,化简1-cos 4α-sin 4α1-cos 6α-sin 6α= 23. (3)(2017·全国卷Ⅰ)已知α∈⎝ ⎛⎭⎪⎫0,π2,tan α=2,则cos ⎝ ⎛⎭⎪⎫α-π4= 31010 .[解析] (1)∵tan α=-512,∴sin αcos α=-512.∵sin 2α+cos 2α=1,∴sin 2α+⎝ ⎛⎭⎪⎫-125sin α2=1,∴sin α=±513.又α为第二象限角,∴sin α=513,故选C.(2)解法一:原式=1-cos 2α1+cos 2α-sin 4α1-cos 2α1+cos 2α+cos 4α-sin 6α =sin 2α1+cos 2α-sin 2αsin 2α1+cos 2α+cos 4α-sin 4α =2cos 2α1+cos 2α+cos 2α-sin 2α =2cos 2α3cos 2α=23. 解法二:∵1-cos 4α-sin 4α=1-(cos 2α+sin 2α)2+2sin 2αcos 2α=2sin 2αcos 2α, ∴原式=2sin 2αcos 2α1-cos 2α+sin 2αcos 4α-cos 2αsin 2α+sin 4α =2sin 2αcos 2α1-cos 4α-sin 4α+cos 2αsin 2α =2sin 2αcos 2α3sin 2αcos 2α=23. (3)由tan α=2得sin α=2cos α. 又sin 2α+cos 2α=1,所以cos 2α=15.因为α∈⎝ ⎛⎭⎪⎫0,π2,所以cos α=55,sin α=255.因为cos ⎝ ⎛⎭⎪⎫α-π4=cos αcos π4+sin αsin π4, 所以cos ⎝ ⎛⎭⎪⎫α-π4=55×22+255×22=31010. 考点二 诱导公式及其应用——多维探究 角度1 利用诱导公式化简三角函数式例2 (1)化简:sin ⎝ ⎛⎭⎪⎫-α-3π2sin ⎝ ⎛⎭⎪⎫3π2-αtan 22π-αcos ⎝ ⎛⎭⎪⎫π2-αcos ⎝ ⎛⎭⎪⎫π2+αsin π+α= -1sin α .(2)化简1-2sin 10°sin 100°cos 80°-1-sin 2170°= -1 . [解析] (1)原式=cos α-cos αtan 2αsin α-sin α-sin α=-cos 2α·sin 2αcos 2αsin 3α=-1sin α. (2)∵cos 10°>sin10°,∴原式=1-2sin 10°cos 10°sin 10°-cos 10°=sin 210°-2sin 10°cos 10°+cos 210°sin 10°-cos 10°=|sin 10°-cos 10°|sin 10°-cos 10°=cos 10°-sin 10°-cos 10°-sin 10°=-1.角度2 “换元法”的应用例3 已知cos ⎝ ⎛⎭⎪⎫π6-θ=a ,则cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ的值是 0 .[解析] 因为cos ⎝⎛⎭⎪⎫5π6+θ=cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-θ =-cos ⎝ ⎛⎭⎪⎫π6-θ=-a.sin ⎝ ⎛⎭⎪⎫2π3-θ=sin ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫π6-θ=cos ⎝ ⎛⎭⎪⎫π6-θ=a ,所以cos ⎝⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ=0. 名师点拨(1)诱导公式的两个应用方向与原则:①求值:化角的原则与方向:负化正,大化小,化到锐角为终了. ②化简:化简的原则与方向:统一角,统一名,同角名少为终了.(2)注意已知中角与所求式子中角隐含的互余、互补关系、巧用诱导公式解题,常见的互余关系有π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等,互补关系有π3+α与2π3-α;π4+α与3π4-α等.〔变式训练2〕(1)(角度1)已知f(α)=sin α-3πcos 2π-αsin ⎝ ⎛⎭⎪⎫-α+3π2cos -π-αsin -π-α.①化简f(α);②若α是第三象限的角,且cos ⎝⎛⎭⎪⎫α-3π2=15,求f(α)的值. (2)(角度2)(2021·唐山模拟)已知α为钝角,sin ⎝ ⎛⎭⎪⎫π4+α=34,则sin ⎝ ⎛⎭⎪⎫π4-α= -74 ,cos ⎝⎛⎭⎪⎫α-π4= 34 .[解析] (1)①f(α)=sin α-3πcos 2π-αsin ⎝ ⎛⎭⎪⎫-α+3π2cos -π-αsin -π-α=-sin α·cos α·-cos α-cos α·sin α=-cos α.②因为cos ⎝ ⎛⎭⎪⎫α-3π2=-sin α,所以sin α=-15. 又α是第三角限的角, 所以cos α=-1-⎝ ⎛⎭⎪⎫-152=-265.所以f(α)=265.(2)sin ⎝⎛⎭⎪⎫π4-α=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4-α=cos ⎝ ⎛⎭⎪⎫π4+α, 因为α为钝角, 所以34π<π4+α<54π,所以cos ⎝ ⎛⎭⎪⎫π4+α<0.所以cos ⎝ ⎛⎭⎪⎫π4+α=-1-⎝ ⎛⎭⎪⎫342=-74.cos ⎝ ⎛⎭⎪⎫α-π4=sin ⎣⎢⎡⎦⎥⎤π2+⎝⎛⎭⎪⎫α-π4=sin ⎝ ⎛⎭⎪⎫π4+α=34.名师讲坛·素养提升sin x +cos x 、sin x -cos x 、sin xcos x 之间的关系例4 (2021·北京东城模拟)已知sin θ+cos θ=713,θ∈(0,π),则tan θ= -125. [解析] 解法一:因为sin θ+cos θ=713,θ∈(0,π)所以(sin θ+cos θ)2=1+2sin θcos θ=49169,sin θcos θ=-60169.由根与系数的关系,知sin θ,cos θ是方程x 2-713x -60169=0的两根,所以x 1=1213,x 2=-513.因为θ∈(0,π),所以sin θ>0.所以sin θ=1213,cos θ=-513,tan θ=sin θcos θ=-125.解法二:同解法一,得sin θcos θ=-60169,所以sin θcos θsin 2θ+cos 2θ=-60169,弦化切,得 tan θtan 2θ+1=-60169,解得tan θ=-125或tan θ=-512. 又θ∈(0,π),sin θ+cos θ=713>0,sin θcos θ=-60169<0.∴θ∈⎝ ⎛⎭⎪⎫π2,π,且sin θ>|cos θ|,∴⎪⎪⎪⎪⎪⎪sin θcos θ=|tan θ|>1,∴tan θ=-125.解法三:解方程组⎩⎪⎨⎪⎧sin θ+cos θ=713,sin 2θ+cos 2θ=1.得⎩⎪⎨⎪⎧sin θ=1213,cos θ=-513或⎩⎪⎨⎪⎧sin θ=-513,cos θ=1213.(舍去)故tan θ=-125.名师点拨sin x +cos x 、sin x -cos x 、sin xcos x 之间的关系为(sin x +cos x)2=1+2sin xcos x ,(sin x -cos x)2=1-2sin xcos x ,(sin x +cos x)2+(sin x -cos x)2=2.因此已知上述三个代数式中的任意一个代数式的值,便可求其余两个代数式的值. 〔变式训练3〕(1)(2021·山东师大附中模拟)已知-π2<α<0,sin α+cos α=15,则1cos 2α-sin 2α的值为( C ) A.75 B .725 C .257D .2425(2)若1sin α+1cos α=3,则s in αcos α=( A )A .-13B .13C .-13或1D .13或-1 [解析] (1)解法一:∵sin α+cos α=15,∴(sin α+cos α)2=125,∴sin αcos α=-1225,又α∈⎝ ⎛⎭⎪⎫-π2,0,∴sin α<0,cos α>0,∴cos α-sin α=sin α-cos α2=1-2sin αcos α=75.∴1cos 2α-sin 2α=1cos α-sin αcos α+sin α=257,故选C. 解法二:由解法一知⎩⎪⎨⎪⎧sin α+cos α=15,sin α-cos α=-75,得⎩⎪⎨⎪⎧cos α=45,sin α=-35.∴tan α=sin αcos α=-34.∴1cos 2α-sin 2α=sin 2α+cos 2αcos 2α-sin 2α=1+tan 2α1-tan 2α =1+9161-916=257,故选C.(2)由1sin α+1cos α=3,可得sin α+cos α=3sin αcos α,两边平方,得1+2sin αcosα=3sin 2αcos 2α,解得sin αcos α=-13或sin αcos α=1.由题意,知-1<sin α<1,-1<cos α<1,且sin α≠0,cos α≠0,所以sin αcos α≠1,故选A.。
【配套K12】2018高考数学大一轮复习第三章三角函数解三角形课时跟踪检测十七同角三角函数的基本关系
课时跟踪检测 (十七) 同角三角函数的基本关系与诱导公式一抓基础,多练小题做到眼疾手快1.若α∈⎝ ⎛⎭⎪⎫-π2,π2,sin α=-35,则cos(-α)=( ) A .-45 B .45C .35D .-35解析:选B 因为α∈⎝ ⎛⎭⎪⎫-π2,π2,sin α=-35,所以cos α=45,即cos(-α)=45. 2.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6B .-π3C .π6D .π3解析:选D ∵sin(π+θ)=-3cos(2π-θ),∴-sin θ=-3cos θ,∴tan θ=3.∵|θ|<π2,∴θ=π3.3.(2017·赣中南五校联考)已知倾斜角为α的直线l 与直线x +2y -3=0垂直,则cos ⎝⎛⎭⎪⎫2 017π2-2α的值为( ) A .45 B .-45C .2D .-12解析:选A 由题意可得tan α=2, 所以cos ⎝⎛⎭⎪⎫2 017π2-2α=sin 2α=2sin αcos αsin 2α+cos 2α=2tan αtan 2α+1=45.故选A . 4.已知α∈⎝ ⎛⎭⎪⎫π2,π,sin α=45,则tan α=________. 解析:∵α∈⎝ ⎛⎭⎪⎫π2,π,∴cos α=-1-sin 2α=-35,∴tan α=sin αcos α=-43.答案:-435.如果sin(π+A )=12,那么cos ⎝ ⎛⎭⎪⎫3π2-A 的值是________.解析:∵sin(π+A )=12,∴-sin A =12.∴cos ⎝⎛⎭⎪⎫3π2-A =-sin A =12.答案:12二保高考,全练题型做到高考达标1.已知tan(α-π)=34,且α∈⎝ ⎛⎭⎪⎫π2,3π2,则sin ⎝ ⎛⎭⎪⎫α+π2=( )A .45 B .-45C .35D .-35解析:选B 因为tan(α-π)=34,所以tan α=34.又因为α∈⎝ ⎛⎭⎪⎫π2,3π2,所以α为第三象限的角,sin ⎝⎛⎭⎪⎫α+π2=cos α=-45.2.已知sin ⎝ ⎛⎭⎪⎫α-π4=13,则cos ⎝ ⎛⎭⎪⎫π4+α=( )A .223B .-223C .13D .-13解析:选D ∵cos ⎝ ⎛⎭⎪⎫π4+α=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α=sin ⎝ ⎛⎭⎪⎫π4-α=-sin ⎝⎛⎭⎪⎫α-π4=-13.3.已知f (x )=a sin(πx +α)+b cos(πx +β)+4,若f (2 016)=5,则f (2 017)的值是( )A .2B .3C .4D .5解析:选B ∵f (2 016)=5,∴a sin(2 016π+α)+b cos(2 016π+β)+4=5,即a sin α+b cos β=1.∴f (2 017)=a sin(2 017π+α)+b cos(2 017π+β)+4=-a sin α-b cos β+4=-1+4=3.4.(2017·广州模拟)当θ为第二象限角,且sin ⎝ ⎛⎭⎪⎫θ2+π2=13时,1-sin θcos θ2-sinθ2的值是( )A .1B .-1C .±1D .0解析:选B ∵sin ⎝ ⎛⎭⎪⎫θ2+π2=13,∴cos θ2=13,∴θ2在第一象限,且cos θ2<sin θ2, ∴1-sin θcos θ2-sin θ2=-⎝ ⎛⎭⎪⎫cos θ2-sin θ2cos θ2-sinθ2=-1.5.计算:cos 350°-2sin 160°-=( )A .- 3B .-32C .32D . 3 解析:选D 原式=----+=cos 10°----=cos 10°-2⎝ ⎛⎭⎪⎫12cos 10°-32sin 10°sin 10°=3.6.已知sin(3π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α,则sin αcos α=________. 解析:∵sin(3π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α, ∴sin α=-2cos α, ∴tan α=-2,∴sin αcos α=sin αcos αsin 2α+cos 2α =tan αtan 2α+1=-2-22+1=-25.答案:-257.已知向量a =(sin θ,-2)与b =(1,cos θ)互相垂直,其中θ∈⎝⎛⎭⎪⎫0,π2,则cosθ=________.解析:∵a ⊥b ,∴a ·b =sin θ-2cos θ=0,即sin θ=2cos θ. 又∵sin 2θ+cos 2θ=1,∴4cos 2θ+cos 2θ=1,即cos 2θ=15,又∵θ∈⎝ ⎛⎭⎪⎫0,π2,∴cos θ=55.答案:558.sin 4π3·cos 5π6·tan ⎝ ⎛⎭⎪⎫-4π3的值是________. 解析:原式=sin ⎝ ⎛⎭⎪⎫π+π3·cos ⎝ ⎛⎭⎪⎫π-π6·tan ⎝ ⎛⎭⎪⎫-π-π3=⎝ ⎛⎭⎪⎫-sin π3·⎝ ⎛⎭⎪⎫-cos π6·⎝ ⎛⎭⎪⎫-tan π3=⎝ ⎛⎭⎪⎫-32×⎝ ⎛⎭⎪⎫-32×(-3)=-334. 答案:-3349.求值:sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 945°. 解:原式=-sin 1 200°·cos 1 290°+cos 1 020°·(-sin 1 050°)+tan 945° =-sin 120°·cos 210°+cos 300°·(-sin 330°)+tan 225° =(-sin 60°)·(-cos 30°)+cos 60°·sin 30°+tan 45° =32×32+12×12+1=2. 10.已知sin(3π+α)=2sin ⎝⎛⎭⎪⎫3π2+α,求下列各式的值:(1)sin α-4cos α5sin α+2cos α; (2)sin 2α+sin 2α.解:由已知得sin α=2cos α. (1)原式=2cos α-4cos α5×2cos α+2cos α=-16.(2)原式=sin 2α+2sin αcos αsin 2α+cos 2α =sin 2α+sin 2αsin 2α+14sin 2α=85.三上台阶,自主选做志在冲刺名校1.sin 21°+sin 22°+…+sin 290°=________.解析:sin 21°+sin 22°+…+sin 290°=sin 21°+sin 22°+…+sin 244°+sin 245°+cos 244°+cos 243°+…+cos 21°+sin 290°=(sin 21°+cos 21°)+(sin 22°+cos 22°)+…+(sin 244°+cos 244°)+sin 245°+sin 290°=44+12+1=912.答案:9122.已知f (x )=cos2n π+x ·sin 2n π-xcos 2n +π-x ](n ∈Z). (1)化简f (x )的表达式;(2)求f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009的值.解:(1)当n 为偶数,即n =2k (k ∈Z)时, f (x )=cos 22k π+x ·sin 22k π-xcos k +π-x ]=cos 2x ·sin 2-xcos 2π-x =cos 2x -sin x2-cos x 2=sin 2x ;当n 为奇数,即n =2k +1(k ∈Z)时, f (x )=cos 2k +π+x ]·sin 2k +π-x ]cos2k ++1]π-x }=cos 2[2k π+π+x ]·sin 2[2k π+π-x ]cos 2k +π+π-x ]=cos2π+x ·sin2π-xcos 2π-x=-cos x 2sin 2x-cos x2=sin 2x ,综上得f (x )=sin 2x .(2)由(1)得f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009=sin 2π2 018+sin 21 008π2 018 =sin 2π2 018+sin 2⎝ ⎛⎭⎪⎫π2-π2 018 =sin2π2 018+cos 2π2 018=1. 倚窗远眺,目光目光尽处必有一座山,那影影绰绰的黛绿色的影,是春天的颜色。
高考数学(文江苏专用)一轮复习课件:第三章第2讲同角三角函数的基本关系与诱导公式
第三章三角函数、解三角形同角三角函数的基本关系与诱导公式教材回顾▼夯实基础课本温故追根求源Ml谋梳理严1.同角三角函数的基本关系式(1)平方关系:sin2a +cos2a =1(«GR);(2)商数关系:tan a =订—A:eZ2.六组诱导公式k兀“亍土a仗已Z)"的三角函数记忆口诀“奇变偶不对于角变,符号看象限”,“奇变偶不变”是指“当k为奇数时, 正弦变余弦,余弦变正弦;当吃为偶数时,函数名不变”.“符号看象限”是指“在久的三角函数值前面加上当。
为锐角时原函数值的符号”.匿0【做二微〕,贝0 sin x = 2 .、JI解得sin x= -1±^52因为一lWsinxWl, 所以 smx=―— 1.已知 tanx=smx+y^| 解析:因为 tanx=sin x+~ ,所以 tanx=cosx, \ /丿 所以 sinx=cos 2x,所以 sinL+sin x —1=0,2.tan 690°的值为—3 解析:tan 690° =tan(—30' =tan(—30° )=—tan 30°3 +2X360° )3 •3.已知cos12=T解析:因为cos 13’角a是第二象限角、则tan(2 —a)角a是第二象限角,故sin a =12 0所以tan 12故tan(2 兀—a)=—tan12要會厂1.必明辨的2个易错点(1)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.(2)注意求值与化简后的结果一般要尽可能有理化、整式化.2.必会的3种方法(三角函数求值与化简的常用方法)⑴弦切互化法:主要利用公式tan a化成正、余弦.⑵和积转换法:利用(sin 0 ±cos 0)2=l±2sin "cos &的关系进行变形、转化.l=sin2e +cos2e =cos2 ^(1+tan2 0)=:(3)巧用“F啲变换( 又因为n,3兀、解析:因为tana=2,所以汨^=2,所以sina=2cos a. 又 sin 2a+cos 2a=l, 所以(2cos a)2+cos 2a=l, 所以 cos 2a=1.已知么丘,tan a =2,贝J cos a =所以COS… M t 2sin a —cos3・若tan a =2,则sin 育囲2sin a —cos a 2tan a —1 sin a +2cos a tan a +2 2X2-1 3 2+24-2.若 sin 0 •cos1 … .cos 0 “ 亠= a刃则5 〃+赢「万的值疋―:解析:tan .cos sin £_sin 0 cos 0 cos i +sin0 _ 0 cos hn=2-;的值为 _____解析:典例剖析▼考点突破*考点一三角函数的诱导公式「茲 sin (k n +a) , cos (k n +a) ,⑶已知*sin Q + cos。
2018版高考一轮总复习数学理课件 第3章 三角函数、解
[双基夯实] 一、疑难辨析 判断 下列 结论 的正 误. ( 正确 的打 “√” ,错 误的打 “×”) 4 1.已知 sinα= ,α∈ 5
π , π ,则 2
3 cosα= .( × ) 5
2.sin(π+ α)=- sin α 成立的条件是 α 为锐角.( × ) 3.六组诱导公式中的角 α 可以是任意角.( √ ) 1 1 4.若 cos(nπ-θ)= (n∈Z),则 cosθ= .( × ) 3 3
sinx=- 3, 5 π ∵- <x<0,∴ 2 4 cosx= , 5
7 ∴ sin x- cosx=- . 5
1 1 2 2 解法二:∵ sinx+ cosx= ,∴ (sinx+ cosx) = , 5 5 1 24 即 1+2sin xcosx= ,∴ 2sinxcosx=- . 25 25
六组诱导公式 π+α
-sin α -cosα tanα
角 2kπ+α (k∈ Z)
-α
-sin α
π-α
π -α 2
π +α 2
sinα
sinα
-cosα -tan α
cosα
sinα—Βιβλιοθήκη cosα-sin α
cosα
tanα
cosα
-tan α
—
[必会结论] 1.特殊角的三角函数值 α sinα cosα tanα 0 0 1 0 π 6 1 2 3 2 3 3 π 4 2 2 2 2 1 π 3 3 2 1 2 3 π 2 1 0 不存在 π 0 -1 0 3π 2 -1 0 不存在
2. 诱导公式可简记为: 奇变偶不变, 符号看象限. “奇” π 与“偶”指的是诱导公式 k·+α 中的整数 k 是奇数还是偶 2 数. “变”与“不变”是指函数的名称的变化, 若 k 是奇数, 则正、余弦互变;若 k 为偶数,则函数名称不变.“符号看 π π 象限”指的是在 k·+α 中, 将 α 看成锐角时 k·+α 所在的 2 2 象限.
高考数学一轮复习第2讲 同角三角函数的基本关系与诱导公式
第2讲 同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系式 (1)平方关系:01sin 2α+cos 2α=1.(2)商数关系:02sinαcosα=tan α.2.六组诱导公式 公式 一 二 三 四 五 六 角 2k π+ α(k ∈Z ) π+α -α π-α π2-απ2+α正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan αtan α-tan α-tan α--口诀函数名不变,符号看象限函数名改变,符号看象限同角三角函数基本关系式的常用变形 (sin α±cos α)2=1±2sin αcos α; (sin α+cos α)2+(sin α-cos α)2=2; (sin α+cos α)2-(sin α-cos α)2=4sin αcos α; sin α=tan αcos α⎝ ⎛⎭⎪⎪⎫α≠π2+kπ,k∈Z ;sin2α=sin2αsin2α+cos2α=tan2αtan2α+1;cos2α=cos2αsin2α+cos2α=1tan2α+1.1.若cosα=13,α∈⎝⎛⎭⎪⎪⎫-π2,0,则tanα等于()A.-24B.24C.-22D.22答案 C解析由已知得sinα=-1-cos2α=-1-19=-223,所以tanα=sinαcosα=-22,选C.2.(2021·大同模拟)若角600°的终边上有一点(-4,a),则a的值是() A.-43B.±43C.3D.43答案 A解析∵tan600°=a-4=tan(540°+60°)=tan60°=3,∴a=-43.故选A.3.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于()A.-π6B.-π3C .π6D .π3答案 D解析 ∵sin(π+θ)=-3cos(2π-θ),∴-sin θ=-3cos θ,∴tan θ=3.∵|θ|<π2,∴θ=π3.4.(2020·杭州学军中学模拟)已知cos31°=a ,则sin239°·tan149°的值为( ) A.1-a2aB .1-a2C.a2-1aD .-1-a2答案 B解析 sin239°tan149°=sin(270°-31°)tan(180°-31°)=-cos31°·(-tan31°)=sin31°=1-a2.5.化简cos ⎝⎛⎭⎪⎪⎫α-π2sin ⎝ ⎛⎭⎪⎪⎫5π2+αsin(α-π)cos(2π-α)的结果为________.答案 -sin 2α 解析 原式=sinαcosα(-sin α)cos α=-sin 2α.6.已知α是第二象限的角,tan α=-12,则cos α=________.答案 -255解析 因为α是第二象限的角,所以sin α>0,cos α<0,由tan α=-12,得sin α=-12cos α,代入sin 2α+cos 2α=1中,得54cos 2α=1,所以cos α=-255.考向一 诱导公式的应用 例1 (1)化简:错误!=________. 答案 -1 解析 原式=错误!=tanαcosαsi n ⎝ ⎛⎭⎪⎪⎫π2+α-cosαsinα=tanαcosαcosα-cosαsinα=-tanαcosαsinα=-sinαcosα·cosαsinα=-1.(2)已知cos(75°+α)=513,α是第三象限角,则sin(195°-α)+cos(α-15°)的值为________.答案 -1713解析 因为cos(75°+α)=513>0,α是第三象限角,所以75°+α是第四象限角, sin(75°+α)=-错误!=-错误!.所以sin(195°-α)+cos(α-15°) =sin[180°+(15°-α)]+cos(15°-α) =-sin(15°-α)+cos(15°-α)=-sin[90°-(75°+α)]+cos[90°-(75°+α)] =-cos(75°+α)+sin(75°+α) =-513-1213=-1713.(3)(2020·潍坊一模)在平面直角坐标系xOy 中,点P (3,1),将向量OP→绕点O 按逆时针方向旋转π2后得到向量OQ→,则点Q 的坐标是________.答案 (-1,3)解析 ∵OP→=(3,1)=(2cos θ,2sin θ),cos θ=32,sin θ=12,∴将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →=⎝ ⎛⎭⎪⎪⎫2cos ⎝ ⎛⎭⎪⎪⎫θ+π2,2sin ⎝ ⎛⎭⎪⎪⎫θ+π2=(-2sin θ,2cos θ)=(-1,3),∴点Q 的坐标是(-1,3).1.诱导公式的两个应用方向与原则(1)求值,化角的原则与方向:负化正,大化小,化到锐角为终了. (2)化简,化简的原则与方向:统一角,统一名,同角名少为终了. 2.含2π整数倍的诱导公式的应用由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cos α.1.(2020·江西宜春中学诊断)若α为锐角,且cos ⎝⎛⎭⎪⎪⎫α+π6=13,则cos ⎝⎛⎭⎪⎪⎫α-π3的值为( )A.223B .23 C .26D .526答案 A解析 ∵0<α<π2,∴π6<α+π6<2π3,∴sin ⎝⎛⎭⎪⎪⎫α+π6=1-cos2⎝⎛⎭⎪⎪⎫α+π6=223,∴cos ⎝ ⎛⎭⎪⎪⎫α-π3=cos ⎝ ⎛⎭⎪⎪⎫α+π6-π2=sin ⎝ ⎛⎭⎪⎪⎫α+π6=223.故选A.2.计算:sin(-1200°)cos1290°=________. 答案34解析 原式=-sin1200°cos1290°=-sin(3×360°+120°)cos(3×360°+210°)=-sin120°cos210°=-sin(180°-60°)cos(180°+30°) =sin60°cos30°=32×32=34.3.化简:错误!. 解 原式=错误!=错误! =错误!=错误!. 多角度探究突破考向二 同角三角函数的基本关系 角度1 切弦互化例2 (1)(2020·唐山第二次模拟)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上一点A (2sin α,3)(sin α≠0),则cos α=( )A.12B .-12C .32D .-32答案 A解析 由三角函数定义,得tan α=32sinα,所以sinαcosα=32sinα,则2(1-cos 2α)=3cos α,所以(2cos α-1)(cos α+2)=0,则cos α=12.(2)(2020·济宁三模)已知tan(π-α)=2,则sinα+cosαsinα-cosα=________.答案13解析 因为tan(π-α)=2,所以tan α=-2,所以sinα+cosαsinα-cosα=tanα+1tanα-1=-2+1-2-1=13. 同角三角函数的基本关系式的功能是根据角的一个三角函数值求其他三角函数值,主要利用商数关系tan α=sinαcosα和平方关系1=sin 2α+cos 2α.4.已知α为锐角,且tan(π-α)+3=0,则sin α等于( )A.13B .31010C .377 D .355答案 B解析 因为tan(π-α)+3=0,所以tan α=3,sin α=3cos α.因为sin 2α+cos 2α=1,所以sin 2α=910. 又因为α为锐角,故sin α=31010.故选B.5.已知α是第二象限角,cos ⎝ ⎛⎭⎪⎪⎫3π2+α=45,则tan α=________.答案 -43解析 ∵cos ⎝ ⎛⎭⎪⎪⎫3π2+α=45,∴sin α=45,又α为第二象限角,∴cos α=-1-sin2α=-35,∴tan α=sinαcosα=-43.角度2 “1”的变换例3 (2021·海口模拟)已知角α的顶点为坐标原点,始边为x 轴的正半轴,终边上有一点P (1,2),则sin2α1-3sinαcosα=________.答案 -4解析 因为角α的终边上有一点P (1,2),所以tan α=2. 所以sin2α1-3sinαcosα=sin2αsin2α+cos2α-3sinαcosα=tan2αtan2α+1-3tanα=2222+1-3×2=-4. 对于含有sin 2α,cos 2α,sin αcos α的三角函数求值题,一般可以考虑添加分母1,再将1用“sin 2α+cos 2α”代替,然后用分子分母同除以角的余弦的平方的方式将其转化为关于tan α的式子,从而求解.6.已知tan α=2,则(1)3sinα-2cosαsinα+cosα=________;(2)23sin 2α+14cos 2α=________. 答案 (1)43 (2)712解析 因为tan α=2,所以, (1)原式=3tanα-2tanα+1=3×2-22+1=43.(2)原式=23·sin2αsin2α+cos2α+14·cos2αsin2α+cos2α =23·tan2αtan2α+1+14·1tan2α+1 =23×2222+1+14×122+1=712. 角度3 sin x +cos x ,sin x -cos x ,sin x cos x 之间的关系例4 (1)已知sin αcos α=18,且5π4<α<3π2,则cos α-sin α的值为( )A .-32B .32C .-34D .34答案 B解析 ∵5π4<α<3π2,∴cos α<0,sin α<0且|cos α|<|sin α|,∴cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×18=34,∴cos α-sin α=32.(2)若θ∈⎝ ⎛⎭⎪⎪⎫π2,π,则 错误!等于( )A .sin θ-cos θB .cos θ-sin θC .±(sin θ-cos θ)D .sin θ+cos θ答案 A 解析 因为错误! =1-2sinθcosθ=错误!=|sin θ-cos θ|,又θ∈⎝ ⎛⎭⎪⎪⎫π2,π,所以sin θ-cos θ>0,所以原式=sin θ-cos θ.故选A.(1)已知a sin x +b cos x =c 可与sin 2x +cos 2x =1联立,求得sin x ,cos x .(2)sin x +cos x ,sin x -cos x ,sin x cos x 之间的关系为 (sin x +cos x )2=1+2sin x cos x , (sin x -cos x )2=1-2sin x cos x , (sin x +cos x )2+(sin x -cos x )2=2.因此,已知上述三个代数式中的任意一个代数式的值,便可求其余两个代数式的值.7.若1sin α+1cosα=3,则sin αcos α=( )A .-13B .13C .-13或1D .13或-1答案 A 解析 由1sinα+1cosα=3,可得sin α+cos α=3sin αcos α,两边平方,得1+2sin αcos α=3sin 2αcos 2α,解得sin αcos α=-13或sin αcos α=1.由题意,知-1<sin α<1,-1<cos α<1,且sin α≠0,cos α≠0,所以sin αcos α≠1.故选A.8.已知sin α+cos α=12,α∈(0,π),则1-tanα1+tanα=( )A .-7B .7 C.3D .-3答案 A解析 因为(sin α+cos α)2=1+2sin αcos α=14,所以sin αcos α=-38,又α∈(0,π),所以sin α>0,cos α<0.因为(sin α-cos α)2=1-2sin αcos α=74,所以cos α-sin α=-72.所以1-tanα1+tanα=cosα-sinαcosα+sinα=-7212=-7.故选A.一、单项选择题1.sin210°cos120°的值为( ) A.14B .-34C .-32D .34答案 A解析 sin210°cos120°=sin(180°+30°)cos(180°-60°)=-sin30°·(-cos60°)=⎝ ⎛⎭⎪⎪⎫-12×⎝ ⎛⎭⎪⎪⎫-12=14.故选A. 2.(2020·潍坊模拟)已知cos ⎝ ⎛⎭⎪⎪⎫3π2-φ=32,且|φ|<π2,则tan φ等于( )A .-33B .33 C .3 D .-3答案 D解析 由cos ⎝ ⎛⎭⎪⎪⎫3π2-φ=-sin φ=32,得sin φ=-32,又|φ|<π2,得到-π2<φ<π2,∴cos φ=1-⎝ ⎛⎭⎪⎪⎫-322=12,则tan φ=-3212=-3.故选D.3.已知α∈⎝ ⎛⎭⎪⎪⎫π2,π,tan α=-34,则sin(α+π)=( )A.35 B .-35C.45 D .-45答案 B解析由题意可知⎩⎪⎨⎪⎧sinαcosα=-34,sin2α+cos2α=1,由此解得sin 2α=925,又α∈⎝ ⎛⎭⎪⎪⎫π2,π,因此有sin α=35,sin(α+π)=-sin α=-35.故选B. 4.已知A =错误!+错误!(k ∈Z ),则A 的值构成的集合是( ) A .{1,-1,2,-2} B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}答案 C解析 当k 为偶数时,A =sinαsinα+cosαcosα=2;当k 为奇数时,A =-sinαsinα-cosαcosα=-2.故A 的值构成的集合是{2,-2}.5.(2020·天津西青区模拟)已知sin α+cos α=-2,则tan α+1tanα=( )A .2B .12C .-2D .-12答案 A解析 ∵sin α+cos α=-2,∴(sin α+cos α)2=2,∴1+2sin αcos α=2,∴sin αcos α=12.tan α+1tanα=sinαcosα+cosαsinα=sin2α+cos2αsinαcosα=112=2.故选A.6.已知sin ⎝ ⎛⎭⎪⎪⎫α-π12=13,则cos ⎝ ⎛⎭⎪⎪⎫α+17π12的值为( ) A.13B .223 C .-13D .-223答案 A解析 由cos ⎝ ⎛⎭⎪⎪⎫α+17π12=cos ⎝ ⎛⎭⎪⎪⎫α-π12+3π2=sin ⎝⎛⎭⎪⎪⎫α-π12=13. 7.(2020·济宁模拟)直线l :2x -y +e =0的倾斜角为α,则sin(π-α)sin ⎝ ⎛⎭⎪⎪⎫π2+α的值为( )A .-25B .-15C .15D .25答案 D解析 ∵直线l :2x -y +e =0的倾斜角为α,∴tan α=2,∴sin(π-α)sin ⎝ ⎛⎭⎪⎪⎫π2+α=sin αcos α=sinαcosαsin2α+cos2α=tanα1+tan2α=21+22=25.故选D.8.化简1+sinα+cosα+2sinαcosα1+sinα+cosα的结果是( )A .2sin αB .2cos αC .sin α+cos αD .sin α-cos α答案 C解析 原式=sin2α+cos2α+2sinαcosα+sinα+cosα1+sinα+cosα=错误! =错误!=sin α+cos α.故选C.9.若sin θ+sin 2θ=1,则cos 2θ+cos 6θ+cos 8θ的值为( ) A .0 B .1 C .-1 D .5-12答案 B解析 由sin θ+sin 2θ=1,得sin θ=1-sin 2θ=cos 2θ,∴cos 2θ+cos 6θ+cos 8θ=sin θ+sin 3θ+sin 4θ=sin θ+sin 2θ(sin θ+sin 2θ)=sin θ+sin 2θ=1.10.(2020·海口模拟)若对任意x ∈R ,都有cos ⎝ ⎛⎭⎪⎪⎫2x -5π6=sin(ωx +φ)(ω∈R ,|φ|<π),则满足条件的有序实数对(ω,φ)的对数为( )A .0B .1C .2D .3 答案 C解析 cos ⎝ ⎛⎭⎪⎪⎫2x -5π6=cos ⎝ ⎛⎭⎪⎪⎫2x -π3-π2=sin ⎝ ⎛⎭⎪⎪⎫2x -π3,由条件知ω=±2.若ω=2,由φ=-π3+2k π(k ∈Z )且|φ|<π,得φ=-π3;若ω=-2,sin(-2x +φ)=sin(2x +π-φ),则π-φ=-π3+2k π(k ∈Z ),所以φ=-2k π+4π3(k ∈Z ),又|φ|<π,则φ=-2π3,故满足条件的有序数对(ω,φ)的对数为2.二、多项选择题11.在△ABC 中,下列结论正确的是( ) A .sin(A +B )=sin C B .sin B +C2=cos A2C .tan(A +B )=-tan C ⎝ ⎛⎭⎪⎪⎫C ≠π2D .cos(A +B )=cos C 答案 ABC解析 在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ;sin B +C2=sin ⎝ ⎛⎭⎪⎪⎫π2-A 2=cos A 2;tan(A +B )=tan(π-C )=-tan C ⎝ ⎛⎭⎪⎪⎫C ≠π2;cos(A +B )=cos(π-C )=-cos C .12.(2020·湖北宜昌高三模拟)定义:角θ与φ都是任意角,若满足θ+φ=π2,则称θ与φ“广义互余”.已知sin(π+α)=-14,下列角β中,可能与角α“广义互余”的是( )A .sin β=154B .cos(π+β)=14C .tan β=15D .tan β=155答案 AC解析 ∵sin(π+α)=-sin α=-14,∴sin α=14,若α+β=π2,则β=π2-α.sin β=sin ⎝ ⎛⎭⎪⎪⎫π2-α=cos α=±154,故A 符合条件;cos(π+β)=-cos ⎝ ⎛⎭⎪⎪⎫π2-α=-sin α=-14,故B 不符合条件;tan β=15,即sin β=15cos β,又sin 2β+cos 2β=1,所以sin β=±154,故C 符合条件;tan β=155,即sin β=155cos β,又sin 2β+cos 2β=1,所以sin β=±64,故D 不符合条件.故选AC.三、填空题13.sin 4π3cos 5π6tan ⎝ ⎛⎭⎪⎪⎫-4π3的值是________.答案 -334解析 原式=sin ⎝ ⎛⎭⎪⎪⎫π+π3cos ⎝ ⎛⎭⎪⎪⎫π-π6tan ⎝ ⎛⎭⎪⎪⎫-π-π3=⎝ ⎛⎭⎪⎪⎫-sin π3⎝ ⎛⎭⎪⎪⎫-cos π6⎝ ⎛⎭⎪⎪⎫-tan π3=⎝⎛⎭⎪⎪⎫-32×⎝ ⎛⎭⎪⎪⎫-32×(-3)=-334.14.已知sin θ=13,则错误!=________.答案98解析 原式=错误!=错误!=错误!=错误!=错误!.15.已知θ是第四象限角,且sin ⎝ ⎛⎭⎪⎪⎫θ+π4=35,则tan ⎝ ⎛⎭⎪⎪⎫θ-π4=________.答案 -43解析 因为θ是第四象限角,且sin ⎝ ⎛⎭⎪⎪⎫θ+π4=35,所以θ+π4为第一象限角,所以cos ⎝ ⎛⎭⎪⎪⎫θ+π4=45,所以tan ⎝ ⎛⎭⎪⎪⎫θ-π4=sin ⎝ ⎛⎭⎪⎪⎫θ-π4cos ⎝ ⎛⎭⎪⎪⎫θ-π4=-cos π2+⎝ ⎛⎭⎪⎪⎫θ-π4sin π2+⎝ ⎛⎭⎪⎪⎫θ-π4=-cos ⎝ ⎛⎭⎪⎪⎫θ+π4sin ⎝⎛⎭⎪⎪⎫θ+π4=-43.16.已知α为第二象限角,则cos α1+tan2α+sin α·1+1tan2α=________.答案 0解析 原式=cos αsin2α+cos2αcos2α+sin αsin2α+cos2αsin2α=cos α1|cosα|+sin α1|sinα|,因为α是第二象限角,所以sin α>0,cos α<0,所以cos α1|cosα|+sin α1|sinα|=-1+1=0,即原式等于0.四、解答题17.已知α为第三象限角,f (α)=错误!.(1)化简f (α);(2)若cos ⎝ ⎛⎭⎪⎪⎫α-3π2=15,求f (α)的值.解 (1)f (α)=错误! =错误!=-cos α.(2)因为cos ⎝ ⎛⎭⎪⎪⎫α-3π2=15,所以-sin α=15,从而sin α=-15.又因为α为第三象限角, 所以cos α=-1-sin2α=-265,所以f (α)=-cos α=265.18.已知tanαtanα-1=-1,求下列各式的值.(1)sinα-3cosαsinα+cosα; (2)sin 2α+sin αcos α+2. 解 由已知得tan α=12.(1)sinα-3cosαsinα+cosα=tanα-3tanα+1=-53. (2)sin 2α+sin αcos α+2=sin2α+sinαcosαsin2α+cos2α+2=tan2α+tanαtan2α+1+2=⎝ ⎛⎭⎪⎪⎫122+12⎝ ⎛⎭⎪⎪⎫122+1+2=135.19.已知0<α<π2,若cos α-sin α=-55,试求2sinαcosα-cosα+11-tanα的值.解 ∵cos α-sin α=-55,∴1-2sin αcos α=15.∴2sin αcos α=45.∴(sin α+cos α)2=1+2sin αcos α=1+45=95.∵0<α<π2,∴sin α+cos α=355.与cos α-sin α=-55联立,解得 cos α=55,sin α=255.∴tan α=2.∴2sinαcosα-cosα+11-tanα=45-55+11-2=55-95. 20.是否存在α∈⎝ ⎛⎭⎪⎪⎫-π2,π2,β∈(0,π),使等式sin(3π-α)=2cos ⎝ ⎛⎭⎪⎪⎫π2-β,3cos(-α)=-2cos(π+β)同时成立?若存在,求出α,β的值;若不存在,说明理由.解 存在.由sin ()3π-α=2cos ⎝ ⎛⎭⎪⎪⎫π2-β得sin α=2sin β,①由3cos(-α)=-2cos(π+β)得3cos α=2cos β,②∴sin 2α+3cos 2α=2(sin 2β+cos 2β)=2,∴1+2cos 2α=2,∴cos 2α=12,又α∈⎝ ⎛⎭⎪⎪⎫-π2,π2,∴cosα=22,从而α=π4或-π4,当α=π4时,由①知sinβ=12,由②知cosβ=32,又β∈(0,π),∴β=π6,当α=-π4时,由①知sinβ=-12,与β∈(0,π)矛盾,舍去.∴存在α=π4,β=π6,符合题意.21 / 21。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲 同角三角函数的基本关系与诱导公式, [学生用书P64])1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:tan α=sin αcos α.2.六组诱导公式简记口诀:把角统一表示为2±α(k ∈Z )的形式,奇变偶不变,符号看象限.1.辨明三个易误点(1)“同角”有两层含义:一是“角相同”,二是代表“任意”一个使三角函数有意义的角.“同角”的概念与角的表达形式有关,如:sin 23α+cos 23α=1,sinα2cosα2=tan α2.(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. (3)注意求值与化简后的结果一般要尽可能有理化、整式化. 2.三角函数求值与化简的三种常用方法(1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化.(3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4=….1.教材习题改编 tan(-233π)的值为( )A .3B .- 3C .33D .-33A [解析] tan (-233π)=tan (-8π+π3)=tan π3= 3.2.已知sin ⎝⎛⎭⎫π2+α=35,α∈⎝⎛⎭⎫0,π2,则sin(π+α)等于( )A .35B .-35C .45D .-45D [解析] 因为sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝ ⎛⎭⎪⎫0,π2,所以cos α=35,所以sin α=45,所以sin(π+α)=-sin α=-45.3.教材习题改编 已知tan α=2,则3sin α-2cos α3sin α+2cos α的值为( )A .1B .-1C .2D .12D [解析] 由tan α=2得sin α=2cos α, 所以原式=6cos α-2cos α6cos α+2cos α=4cos α8cos α=12.4.教材习题改编 化简(1+tan 2α)cos 2α的结果为________.[解析] 原式=(1+sin 2αcos 2α)cos 2α=cos 2α+sin 2α=1.[答案] 15.教材习题改编 若sin α-cos α=13,则sin αcos α=________.[解析] 由sin α-cos α=13得(sin α-cos α)2=19,即1-2sin αcos α=19,所以2sin αcos α=89,即sin αcos α=49.[答案] 49同角三角函数基本关系式(高频考点)[学生用书P64]同角三角函数的基本关系式的应用很广泛,也比较灵活.在高考中常以选择题、填空题的形式出现.高考对同角三角函数基本关系式的考查主要有以下三个命题角度: (1)知弦求弦; (2)知弦求切; (3)知切求弦.[典例引领](1)(2016·高考全国卷丙)若tan α=34,则cos 2α+2sin 2α=( )A .6425B .4825C .1D .1625(2)(2017·南京模拟)已知α为第二象限角,则cos α·1+tan 2α+sin α 1+1tan 2α=________.【解析】 (1)法一:由tan α=sin αcos α=34,cos 2α+sin 2α=1,得⎩⎨⎧sin α=35,cos α=45或⎩⎨⎧sin α=-35,cos α=-45,则sin 2α=2sin αcos α=2425,则cos 2α+2sin 2α=1625+4825=6425.法二:cos 2α+2sin 2α=cos 2α+4sin αcos αcos 2α+sin 2α=1+4tan α1+tan 2α=1+31+916=6425. (2)原式=cos α sin 2α+cos 2αcos 2α+sin αsin 2α+cos 2αsin 2α=cos α·1|cos α|+sin α·1|sin α|,因为α是第二象限角,所以sin α>0,cos α<0,所以cos α·1|cos α|+sin α·1|sin α|=-1+1=0,即原式等于0.【答案】 (1)A (2)0求解此类问题的关键是:通过平方关系,对称式sin α+cos α,sin α-cos α,sin αcos α之间可建立联系.若令sin α+cos α=t ,则sin αcos α=t 2-12,sin α-cos α=±2-t 2(注意根据α的范围选取正负号),这种关系在三角函数式的化简、求值、证明中十分有用.[题点通关]角度一 知弦求弦1.已知x ∈(-π,0),sin x +cos x =15.(1)求sin x -cos x 的值;(2)求sin 2x +2sin 2x 1-tan x的值.[解] (1)由sin x +cos x =15,平方得sin 2x +2sin x cos x +cos 2x =125,整理得2sin x cos x =-2425.所以(sin x -cos x )2=1-2sin x cos x =4925.由x ∈(-π,0),知sin x <0, 又sin x +cos x >0,所以cos x >0,sin x -cos x <0,故sin x -cos x =-75.(2)sin 2x +2sin 2x 1-tan x =2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x=-2425×1575=-24175.角度二 知弦求切2.(2017·辽宁省五校高三联考)已知cos ⎝⎛⎭⎫π2+α=35,且α∈⎝⎛⎭⎫π2,3π2,则tan α=( )A .43B .34C .-34D .±34B [解析] 因为cos ⎝ ⎛⎭⎪⎫π2+α=35,所以sin α=-35,显然α在第三象限,所以cos α=-45,故tan α=34.角度三 知切求弦3.若sin α=2sin β,tan α=3tan β,则cos α=________.[解析] 因为sin α=2sin β,① tan α=3tan β, tan 2α=9tan 2β.②由①2÷②得:9cos 2α=4cos 2β.③ 由①2+③得sin 2α+9cos 2α=4. 又sin 2α+cos 2α=1,所以cos 2α=38,所以cos α=±64.[答案] ±64诱导公式的应用[学生用书P65][典例引领](1)sin(-1 200°)cos 1 290°=________.(2)设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos⎝⎛⎭⎫3π2+α-sin 2⎝⎛⎭⎫π2+α(1+2sin α≠0),则f ⎝⎛⎭⎫-23π6=________.【解析】 (1)原式=-sin 1 200°cos 1 290° =-sin(3×360°+120°)cos(3×360°+210°) =-sin 120°cos 210°=-sin(180°-60°)cos(180°+30°) =sin 60°cos 30°=32×32=34. (2)因为f (α)=(-2sin α)(-cos α)+cos α1+sin 2α+sin α-cos 2α =2sin αcos α+cos α2sin 2α+sin α=cos α(1+2sin α)sin α(1+2sin α)=1tan α, 所以f ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝⎛⎭⎪⎫-4π+π6=1tan π6= 3. 【答案】 (1)34(2)3(1)诱导公式用法的一般思路①化负为正,化大为小,化到锐角为止.②角中含有加减π2的整数倍时,用公式去掉π2的整数倍.(2)常见的互余和互补的角①常见的互余的角:π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等.②常见的互补的角:π3+θ与2π3-θ;π4+θ与3π4-θ等.(3)三角函数式化简的方向 ①切化弦,统一名. ②用诱导公式,统一角.③用因式分解将式子变形,化为最简.[通关练习]1.(2016·高考全国卷乙)已知θ是第四象限角,且sin ⎝⎛⎭⎫θ+π4=35,则tan ⎝⎛⎭⎫θ-π4=________.[解析] 因为sin ⎝ ⎛⎭⎪⎫θ+π4=35,所以cos ⎝ ⎛⎭⎪⎫θ-π4=sin ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫θ-π4=sin ⎝ ⎛⎭⎪⎫θ+π4=35,因为θ为第四象限角,所以-π2+2k π<θ<2k π,k ∈Z ,所以-3π4+2k π<θ-π4<2k π-π4,k ∈Z ,所以sin ⎝ ⎛⎭⎪⎫θ-π4=-1-⎝⎛⎭⎫352=-45,所以tan ⎝ ⎛⎭⎪⎫θ-π4=sin ⎝ ⎛⎭⎪⎫θ-π4cos ⎝ ⎛⎭⎪⎫θ-π4=-43.[答案] -432.若sin α是方程5x 2-7x -6=0的根,则sin (-α-3π2)sin (3π2-α)tan 2(2π-α)cos (π2-α)cos (π2+α)sin (π+α)=( )A .35B .53C .45D .54B [解析] 方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35.原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sinα=53.,[学生用书P253(独立成册)])1.已知sin(2π-α)=45,α∈⎝⎛⎭⎫3π2,2π,则tan(π-α)=( )A .34B .-43C .-34D .43D [解析] 由sin(2π-α)=45,得sin α=-45.因为α∈⎝⎛⎭⎫32π,2π,所以cos α=35,所以tan α=-43. 故tan(π-α)=-tan α=43.故选D.2.(2017·成都外国语学校月考)已知tan(α-π)=34,且α∈⎝⎛⎭⎫π2,3π2,则sin ⎝⎛⎭⎫α+π2=( )A .45B .-45C .35D .-35B [解析] 由tan(α-π)=34⇒tan α=34.又因为α∈⎝ ⎛⎭⎪⎫π2,3π2,所以α为第三象限的角,sin ⎝ ⎛⎭⎪⎫α+π2=cos α=-45.3.(2017·哈尔滨模拟)已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( ) A .-π6B .-π3C .π6D .π3D [解析] 因为sin(π+θ)=-3cos(2π-θ), 所以-sin θ=-3cos θ,所以tan θ= 3. 因为|θ|<π2,所以θ=π3.4.已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭⎫π4+α=( )A .223B .-223C .13D .-13D [解析] cos ⎝ ⎛⎭⎪⎫π4+α=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α=sin ⎝ ⎛⎭⎪⎫π4-α=-sin ⎝ ⎛⎭⎪⎫α-π4=-13.5.(2017·杭州一模)已知f (α)=cos ⎝⎛⎭⎫π2+αsin ⎝⎛⎭⎫3π2-αcos (-π-α)tan (π-α),则f ⎝⎛⎭⎫-253π的值为( ) A .12 B .-12C .32D .-32A [解析] 由于f (α)=cos ⎝ ⎛⎭⎪⎫π2+αsin ⎝ ⎛⎭⎪⎫3π2-αcos (-π-α)tan (π-α)=sin αcos αcos αtan α=cos α,所以f ⎝⎛⎭⎫-253π=cos ⎝⎛⎭⎫-253π=cos ⎝⎛⎭⎪⎫-8π-π3=12. 6.已知sin α+2cos α=3,则tan α=( )A .22B . 2C .-22 D .- 2A [解析] 因为sin α+2cos α=3, 所以(sin α+2cos α)2=3,所以sin 2α+22sin αcos α+2cos 2α=3, 所以sin 2α+22sin αcos α+2cos 2αsin 2α+cos 2α=3,所以tan 2α+22tan α+2tan 2α+1=3,所以2tan 2α-22tan α+1=0,所以tan α=22. 7.化简:cos (α-π)sin (π-α)·sin(α-π2)·cos(3π2-α)=________.[解析] cos (α-π)sin (π-α)·sin(α-π2)·cos(3π2-α)=-cos αsin α·(-cos α)·(-sin α)=-cos 2α.[答案] -cos 2α8.sin 43π·cos 56π·tan ⎝⎛⎭⎫-43π的值是________. [解析] 原式=sin ⎝ ⎛⎭⎪⎫π+π3·cos ⎝⎛⎭⎪⎫π-π6·tan ⎝ ⎛⎭⎪⎫-π-π3=⎝⎛⎭⎪⎫-sin π3·⎝ ⎛⎭⎪⎫-cos π6·⎝ ⎛⎭⎪⎫-tan π3=⎝⎛⎭⎫-32×⎝⎛⎭⎫-32×(-3)=-334.[答案] -3349.若f (α)=sin[(k +1)π+α]·cos[(k +1)π-α]sin (k π-α)·cos (k π+α)(k ∈Z ),则f (2 017)=________.[解析] ①当k 为偶数时,设k =2n (n ∈Z ), 原式=sin (2n π+π+α)·cos (2n π+π-α)sin (-α)·cos α=sin (π+α)·cos (π-α)-sin α·cos α=-1;②当k 为奇数时,设k =2n +1(n ∈Z ), 原式=sin[(2n +2)π+α]·cos[(2n +2)π-α]sin[(2n +1)π-α]·cos[(2n +1)π+α]=sin α·cos (-α)sin (π-α)·cos (π+α)=-1. 综上所述,当k ∈Z 时,f (α)=-1,故f (2 017)=-1. [答案] -110.若sin θ+cos θsin θ-cos θ=2,则sin(θ-5π)sin ⎝⎛⎭⎫3π2-θ=________.[解析] 由sin θ+cos θsin θ-cos θ=2,得sin θ+cos θ=2(sin θ-cos θ),两边平方得1+2sin θcos θ=4(1-2sin θcos θ),故sin θcos θ=310,所以sin(θ-5π)sin ⎝⎛⎭⎪⎫3π2-θ=sin θcos θ=310.[答案]31011.已知sin α=255,求tan(α+π)+sin ⎝⎛⎭⎫5π2+αcos⎝⎛⎭⎫5π2-α的值.[解] 因为sin α=255>0,所以α为第一或第二象限角.tan(α+π)+sin ⎝⎛⎭⎪⎫5π2+αcos ⎝ ⎛⎭⎪⎫5π2-α=tan α+cos αsin α=sin αcos α+cos αsin α=1sin αcos α. (1)当α是第一象限角时,cos α=1-sin 2α=55, 原式=1sin αcos α=52.(2)当α是第二象限角时,cos α=-1-sin 2α=-55, 原式=1sin αcosα=-52.12.设θ为第二象限角,若tan ⎝⎛⎭⎫θ+π4=12,则sin θ+cos θ=________.[解析] 因为tan ⎝ ⎛⎭⎪⎫θ+π4=12,所以1+tan θ1-tan θ=12,解得tan θ=-13.所以(sin θ+cos θ)2=sin 2θ+cos 2θ+2sin θcos θsin 2θ+cos 2θ=tan 2θ+2tan θ+1tan 2θ+1=19-23+119+1=25.因为θ为第二象限角,tan θ=-13,所以2k π+3π4<θ<2k π+π,k ∈Z ,所以sin θ+cos θ<0, 所以sin θ+cos θ=-105. [答案] -10513.已知sin α=1-sin ⎝⎛⎭⎫π2+β,求sin 2α+sin ⎝⎛⎭⎫π2-β+1的取值范围.[解] 因为sin α=1-sin ⎝ ⎛⎭⎪⎫π2+β=1-cos β,所以cos β=1-sin α. 因为-1≤cos β≤1,所以-1≤1-sin α≤1,0≤sin α≤2, 又-1≤sin α≤1,所以sin α∈[0,1].所以sin 2α+sin ⎝ ⎛⎭⎪⎫π2-β+1=sin 2α+cos β+1=sin 2α-sin α+2=⎝⎛⎭⎫sin α-122+74(*).又sin α∈[0,1],所以当sin α=12时,(*)式取得最小值74;当sin α=1或sin α=0时,(*)式取得最大值2,故所求范围为⎣⎡⎦⎤74,2.14.已知关于x 的方程2x 2-(3+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:(1)sin 2 θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;(3)方程的两根及此时θ的值.[解] (1)原式=sin 2θsin θ-cos θ+cos θ1-sin θcos θ=sin 2θsin θ-cos θ+cos 2θcos θ-sin θ=sin 2θ-cos 2θsin θ-cos θ=sin θ+cos θ.由条件知sin θ+cos θ=3+12,故sin 2θsin θ-cos θ+cos θ1-tan θ=3+12.(2)由已知,得sin θ+cos θ=3+12,sin θcos θ=m2,又1+2sin θcos θ=(sin θ+cos θ)2,可得m =32.(3)由⎩⎪⎨⎪⎧sin θ+cos θ=3+12,sin θcos θ=34知⎩⎨⎧sin θ=32,cos θ=12,或⎩⎨⎧sin θ=12,cos θ=32.π6或θ=π3.又θ∈(0,2π),故θ=。
