山东理工大学离散数学07-08年试题
《离散数学》试题及答案

《离散数学》试题及答案一、选择题(每题5分,共25分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},则A∩B的结果是()A. {1,2,3,4,5}B. {2,4}C. {1,3,5}D. {1,2,3,4,5,6,8,10}答案:B2. 下列关系中,哪个是等价关系?()A. ≤B. ≠C. |D. ≠答案:A3. 设图G有5个顶点,每两个顶点之间都有一条边相连,则图G的边数是()A. 5B. 10C. 15D. 20答案:C4. 下列哪一个图是欧拉图?()A. 无向图B. 有向图C. 树D. 环答案:D5. 下列哪一个命题是正确的?()A. 若p→q为真,则p为真B. 若p∧q为假,则p为假C. 若p∨q为真,则q为真D. 若p→q为假,则p为假答案:B二、填空题(每题5分,共25分)1. 设集合A={a,b,c,d},B={c,d,e},则A-B=________。
答案:{a,b}2. 设p是命题“今天是晴天”,q是命题“我去公园玩”,则命题“如果今天不是晴天,那么我不去公园玩”可以表示为________。
答案:¬p→¬q3. 设图G有n个顶点,e条边,则图G的度数之和为________。
答案:2e4. 一个连通图至少有________个顶点。
答案:25. 设图G的邻接矩阵为A,则A的转置矩阵表示________。
答案:图G的转置图三、判断题(每题5分,共25分)1. 离散数学是研究离散结构的数学分支。
()答案:正确2. 两个集合的笛卡尔积是这两个集合的直积。
()答案:正确3. 有向图中,顶点u和顶点v之间的长度为2的路径是指路径上有3条边。
()答案:错误4. 树是一种无向图。
()答案:正确5. 哈夫曼编码是一种贪心算法。
()答案:正确四、应用题(每题25分,共50分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},C={3,6,9,12,15},求A∪(B∩C)。
2008《离散数学》考试试卷(A卷)

海南大学2008-2009学年度第1学期试卷科目:《离散数学》试题(A卷)姓名:学号:学院:信息科学技术学院专业班级: 07级计算机阅卷教师: 200 年月日考试说明:本课程为闭卷考试,可携带计算器。
一、选择题:(每题2分,共20分)在以下各小题中画有()处填上答案。
1. 下述哪一个不是命题?()。
A.在整数集中不存在最大奇数;B.海口是海南省的省会;C.若我有空,我就运动;D.x+8=10。
2. 命题22∀∃+=的意义是()。
(1)x y x yA.对任何x均存在y使得x2+y2=1;B.对任何y均存在x使得x2+y2=1;C.存在y对任何x均使得x2+y2=1;D.存在x对任何y均使得x2+y2=1;3. 设S={1, 2, 3, 4, 5},则下列集合中是S的真子集的是()。
A.{1, 2, 3, 4}B.{x | x是整数且x2≤25}C.{x | x是正整数且x≤5}D.{x | x是有理数且x≤5}4. 设A={a,b,c},B={1,2,3},以下哪一个关系是从A到B的一一对应函数?()A. f={<a,2>,<b,2>,<c,1>}B. f={<a,1>,<b,2>,<c,3>}C. f={<a,1>,<b,2>,<c,3>,<a,3>}D. f={<a,1>,<b,2>}5. 图1哈斯图所示的偏序集为格的是()。
6. 设有无向图如图2,则()是一条哈密顿回路。
A.gabcdefg B.abcdefg C.cfabcdeg D.efgabcd 7. 哪个顶点可成为图3的割点?()A. aB. bC. cD. d8. 图4中()是欧拉图。
9. 下列()是满2元树。
10.图6中( )是平面图。
二、填空题:(每空2分,共20分)在以下各小题中画有_______处填上答案。
大学试卷《离散数学》及答案.docx

离散数学一、填空题(本大题共48分,共16小题,每小题3分)1.--公式为之充分必要条件是其合取范式之每一合取项中均必同时包含一命题变元及其否定2.无向图G具有是生成树,当且仅当的,若G为(n,m)连通图,要确定G的一棵生成树必删掉G的条边。
3.一个无向图的欧拉回路要求经过图中一次且仅一次,汉密顿图要求经过图中一次且仅一次。
4.设P:我生病,Q:我去学校(1)命题“我虽然生病但我仍去学校”符号化为o (2)命题“只有生病的时候,我才不去学校”符号化为o (3)命题"如果我生病,那么我不去学校”符号化为o5.设有33盏灯,拟公用一个电源,则至少需要5个插头的接线板数6.若HlAH2A-AHn是 ,则称Hl, H2, -Hn是相容的,若HlAH2A-AHn是 ,则称H1.H2, -Hn是不相容的7.设f,g,h 是N 到N上的函数(N 为自然数集合),f(n)=n+l;g(n)=2n;h(n)=0;贝lj(fdg)oh=8.K5的点连通度为 ,边连通度为o9.A={1, 2, 3, 4, 5, 6, 8, 10, 24, 36}, R 是A 上的整除关系。
子B={1, 2, 3, 4},那么B的上界是; B的下界是;:6的上确界是; B的下确界为10.命题公式P-*QAR的对偶式为11.设入={1, {2}, <t>},则A的幕集有元素个。
12.设A={0, 1,2, 3}, B={4,6, 7}, C={8, 9, 12, 14}, R1 是由A 到B 的关系,R2 是由B到C原关系,分别定义为Rl={<2, 6>, <3, 4>, <0, 7>} ;R2={<4, 8>, <4, 12>, <6, 12>,〈7, 14〉},则复合关系RloR2 为:13.设A= {<i)}, B={<t>, (<!>}},贝i]P(A) nP(B)= 。
离散数学-2007`2008(2)-试卷(毕业生)参考答案及评分细则
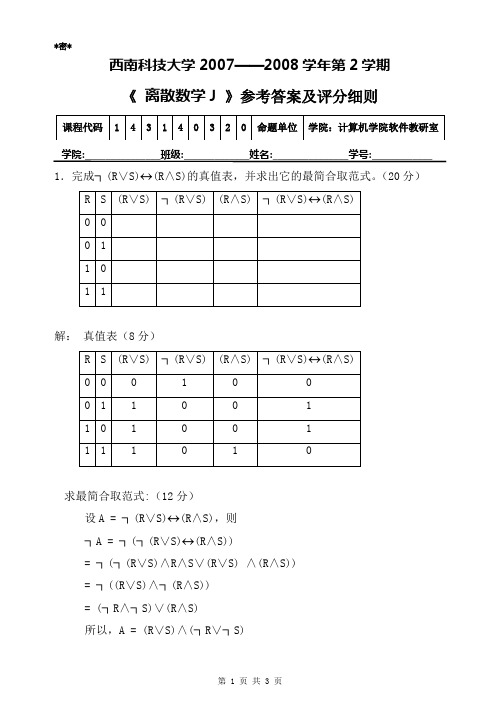
西南科技大学2007——2008学年第2学期《离散数学J 》参考答案及评分细则学院:_______________班级:_____________姓名:_______________学号:____________ 1.完成┐(R∨S)↔(R∧S)的真值表,并求出它的最简合取范式。
(20分)解:真值表(8分)求最简合取范式:(12分)设A = ┐(R∨S)↔(R∧S),则┐A = ┐(┐(R∨S)↔(R∧S))= ┐(┐(R∨S)∧R∧S∨(R∨S) ∧(R∧S))= ┐((R∨S)∧┐(R∧S))= (┐R∧┐S)∨(R∧S)所以,A = (R∨S)∧(┐R∨┐S)2.“同班同学有同一个班主任,张三和李四的班主任不是同一个人,所以张三和李四不是同班同学。
”将上述命题谓词符号化,并证明。
(20分)其中P(x,y):x和y是同班同学,Q(x,y):x和y有同一个班主任,a:张三,b:李四。
解:符号化:(5分)前提:∀x∀y(P(x,y)→Q(x,y)), ┐Q(x,y)结论:┐P(a,b)推理证明:(15分)(1)∀x∀y(P(x,y)→Q(x,y)) P(2)∀y(P(a,y)→Q(a,y)) T,(1),US(3)P(a,b)→Q(a,b) T,(2),US(4)┐Q(a,b) P(5)┐P(a,b) T,(3,4),I43.写出集合{{φ,a},{a}}的全部子集合(8分)解:子集有:φ,{{φ,a}},{{φ}},{{φ,a},{a}}4.某班学生40人,会排球的有20人,会篮球的15人,以上两种运动都会的5人,问两种运动都不会的有几人?(12分)解:设会排球的是集合A,会篮球的是集合B。
则|A∪B|=|A|+|B|-|A∩B|=20+15-5=30所以,两种运动都不会的有40-30=10人。
5.设R是从集合A到集合B的关系,S,T是从集合B到集合C的关系,试证明R(S∩T)⊆(RS)∩(RT) (15分)证明:对任意<a,c>∈Rο(S∩T),则由合成运算知,至少存在b∈B,使得:<a,b>∈R ,<b,c>∈(S∩T),即:<b,c>∈S,且<b,c>∈T。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x)),x R(x) x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠ 且B≠ ,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
B答案 离散期末考试(2010-11_08级)卷

————————¤—————¤———————————装订线————————¤———————¤——————北华大学2010-2011学年第1学期 《离散数学》课程期末考试试卷(B )一、填空(每空4分,共40分)1. 命题公式A 是由n 个命题变项构成的公式,若A 可表成s 个极大项之合取,则A 可同时表为_2n s -_____极小项之析取.2.设令集合A={{1,2},β},B={a ,b},C={b ,{φ}}则笛卡儿积A ×(B ∪C )=_{1,,1,,1,{},2,,2,,2,{}}a b a b φφ<><><><><><>.3.若函数f :A →B,g :B →C 均是单射,则f 和g 的复合函数f ·g :A →C 是___单射_________.4. 左图是___单向_________(弱、单向、强)连通图.5.画出集合表达式A ⊕(B ⋃C)的文氏图(其中A 、B 、C 为全集E 的子集):_________________________.6.对任意集合A ,B ,C 确定下列命题为真的是_____C____.A. 若A ∈B 及B ⊆C ,则A ⊆C; B. 若A ⊆B 及B ∈C ,则A ∈C ; C. 若A ∈B 及B ⊆C ,则A ∈C ; D.若A ⊆B 及B ∈C ,则A ⊆C . 7.设R 和S 是集合A 上的两个二元关系,则下列____B____是正确的.B. 若R 与S 均具有自反性,则R —S 具有自反性;B.若R 与S 均具有反对称性,则R ∪S 具有反对称性;C. 若R 与S 均具有传递性,则R ∩S 具有传递性;D.若R 与S 均具有对称性,则RoS 具有对称性;8.设集合A 含有2个元素,则A 上的函数(从A 到A 的函数)为___B_____个.A.16B.4C.8D.329.设<A,≤>是一个偏序集,取B 是A 的真子集,则必有_____A____.A.集合B 必有极大元和极小元;B.集合B 必有极大元和最小上界;C.集合B 必有最大元和最小元;D.集合B 必有极小元和最大下界.10.设Z 为实数集合,(),Z +是群,则53-=( D ). A.-3 B.-5 C.-6 D.-15二、(本题10分)设集合A={1,2,3,4,5,6,7,8,9,10},R 是A 上的二元关系,其中R={〈x ,y 〉|x ,y ∈A ∧x+y=10 } (1) 写出R 的关系矩阵M ; (2)作R 的关系图G ;(3)根据关系图G 说明R 所具有的性质和不具有的性质 解(3)关系R 具有对称性,不具有自反性,传递性。
2008级离散数学试题答案
2008级离散数学A 卷试题参考答案一、填空题(每小题2分,共20分) 1.(p∧┐q)∨(┐p∧q) 2.┐∀x ∀y (F(x )∧G(y )→H(x ,y )) 3.(F(a, a )∨F(a, b))∧( F(b, a)∨F(b, a)) 4.245 5.e6.a, a 5, a 7, a 11 7.交换律、结合律和吸收律 8.19.r=s10.G 是连通图二、判断题(每小题2分,共20分,正确的划v ,错误的划×) 1.v 2.× 3.× 4.v 5.× 6.×7.v8.×9.v10.v三、计算题(每小题5分,共15分) 1.m1∨m3∨m5∨m72.令f : N×N→N,f (<x,y>) = x 3.6四、证明题(共45分)1.必要性:假设An B?∅,必有x 属于An B ,则x 属于A 同时属于B ,即x 属于A 但是x 不属于A B −,与A B A −=矛盾。
充分性:显然A B A −⊆,下面证明A A B ⊆−。
任取x ,有 x ∈A ⇒ x ∈An E ⇒ x ∈An(B ∪~B) ⇒ x ∈(An B)∪(An ~B) ⇒ x ∈An B ∨ x ∈An ~B ⇒ x ∈An B ∨ x ∈A-B⇒ x ∈A-B (因为An B=∅) 综上上述命题得证。
2.①()F a前提引入 ②(()())x F x G x ∀→ 前提引入 ③()()F a G a → ②UI ④()G a ①③假言推理 ⑤()H a前提引入 ⑥(()()())x G x H x I x ∀∧→ 前提引入 ⑦()()()G a H a I a ∧→⑥UI ⑧()()G a H a ∧ ④⑤合取 ⑨()I a⑦⑧假言推理 3. (1)因为p→p为永真式,所以 pRp,R满足自反性。
(2)若pRq和qRp,则pRq∧qRp ⇔ (p→q)∧(q→p)⇔ p↔q,由于p→q和q→p为永真式,故p↔q为真,即 p与q等价,R满足反对称性。
离散数学试题及答案1(理工大学)
离散数学试题及答案1(计算机科学与技术)一、单选题(题数:25,共 50.0 分)1不是可满足的公式必永()。
(2.0分)A、假B、真C、负D、正正确答案:A2方法简单但是里面充满了()(2.0分)A、方法论B、推广C、推理D、公式正确答案:A3在联结词的集合Ω中如果一个联结词可以用集合Ω中的其它联结词(),则该联结词在Ω中被称为是冗余的,否则该联结词被称为是独立的。
(2.0分)A、表示B、代言C、规划D、条件正确答案:A4在一阶谓词逻辑的()中,所有命题逻辑的推理规则都要继承下来(2.0分)A、推理B、公式C、检查D、发展正确答案:A5首先求出公式G的无ヨ前束型()(2.0分)A、公式B、实数C、分数D、结构正确答案:A6对()中出现的个体常项,指定一个D中的元素(2.0分)A、AB、FC、GD、V正确答案:A7个体常元:通常用排在前面的小写字毋及其下标()(2.0分)A、表示B、发展C、位置D、幅度正确答案:A8谓词逻辑的任一()A,都可化为和应的ヨ前束范式,并且A是普有效的当且仅当其前東范式是普遍有效的。
(2.0分)A、公式B、检查C、发展D、规划正确答案:A9方法简单但是里面充满了()(2.0分)A、方法论B、推广C、推理D、公式正确答案:A10度为()的顶点称为悬点,与悬点关联的边称为悬边(2.0分)A、1B、2C、3D、4正确答案:A11A,B是命题(),若A→B是永真式,则称A永真蕴含B(2.0分)A、公式B、证明C、发展D、研究正确答案:A12命题公式的主范式包括主()范式和主合取范式两种。
(2.0分)A、析取B、完整C、大众D、发展正确答案:A13在一阶谓词逻辑的()中,所有命题逻辑的推理规则都要继承下来(2.0分)A、推理B、公式C、检查D、发展正确答案:A14如果命题公式A在任意的真值赋值()下的真值都为0,则称A为永假式(或称矛盾式)(2.0分)A、函数B、结果C、大小D、位置正确答案:A15A,B是命题公式,若A→B是(),则称A永真蕴含B(2.0分)A、永真式B、不等式C、法线D、结构式正确答案:A16设公式()和B都是限制性公式(2.0分)A、AB、BC、CD、D正确答案:A17{0,1}上的n元函数f:{0,1}n→{0,1}称为一个n元()函数。
山东理工大学《离散数学》答案及评分细则
计算机科学与技术 一 二 三
考核性质 四 五
考试 六
闭 卷 七
命题教师 八
张艳华 石少俭 九 十
考试时间
100 分钟 总分
十一
P F F T T
(3 分)
四、 (10 分). 设正整数的序偶集合 A,在 A 上定义二元关系 R 如下: <<x,y>,<u,v>>∈R,当且仅当 xv=yu, 证明:R 是 A 上的等价关系。 证明:1)自反:因为 <x,y>∈A,xy=yx 2)对称:因为 <<x,y>,<u,v>>∈R 所以<<x,y>,<x,y>>∈R (3 分) (3 分)
g 对应的前缀码为:1101
(4 分) 评分细则:每写错两个字母前缀码扣 1 分。
共
3 页
第
3 页
xv=yu, uy=vx, 所以<<u,v>,<x,y>>∈R
)传递:因为如果<<x,y>,<u,v>>∈R , <<u,v>,<s,t>>∈R ,xv=yu,ut=vs,xvut=yuvs,xt=ys, 所以<<x,y>,<s,t>>∈R (4 分)
共 3 页
第 1 页 2
页
山东理工大学《离散数学》试卷纸
(A )卷 第 2007-2008 学年第 二 学期 班级: 姓名: 学号: …………………………………装……………………………订…………………………线………….………………………………
八、 (10 分)
离散数学试题及答案
离散数学试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个选项不是集合的运算?A. 并集B. 交集C. 差集D. 乘法2. 命题逻辑中,下列哪个命题是真命题?A. (P ∧ ¬P) → QB. (P ∨ Q) ∧ ¬(P ∧ Q)C. P → (Q → P)D. (P → Q) ∧ (Q → R) → (P → R)3. 函数f: A → B,如果f是单射,那么下列哪个选项是正确的?A. A中不同的元素在B中可能有相同的像B. B中每个元素都有原像C. A中不同的元素在B中有不同的像D. B中不同的元素在A中有不同的原像4. 在图论中,下列哪个选项不是图的基本术语?A. 顶点B. 边C. 邻接D. 矩阵5. 组合数学中,从n个不同元素中取出k个元素的组合数记作C(n, k),下列哪个选项是错误的?A. C(n, k) = C(n, n-k)B. C(n, 0) = 1C. C(n, 1) = nD. C(n, k) = C(k, n)6. 关系R是A×B上的二元关系,下列哪个选项不是关系R的性质?A. 自反性B. 对称性C. 传递性D. 可数性7. 在命题逻辑中,下列哪个命题等价于P ∨ (Q ∧ R)?A. (P ∨ Q) ∧ (P ∨ R)B. (P ∧ Q) ∨ (P ∧ R)C. (P ∨ Q) ∨ RD. (P ∨ Q) ∧ R8. 集合{1, 2, 3}的幂集含有多少个元素?A. 3B. 6C. 8D. 99. 在图论中,下列哪个选项不是树的性质?A. 无环B. 至少有两个顶点C. 任意两个顶点都由唯一路径连接D. 至少有一个环10. 在集合论中,下列哪个选项是正确的?A. 空集是任何集合的子集B. 任何集合都是其自身的超集C. 空集是任何非空集合的真子集D. 空集是其自身的并集二、简答题(每题10分,共30分)11. 简述命题逻辑中的德摩根定律,并给出一个例子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P ((P Q) (Q P)) 的主合取范式为 P Q
(3 分)
方法二:真值表法
P Q P ((P Q) (Q P))
FFT
FTT
TFF
TTT
(4 分)
P ((P Q) (Q P)) 的主析取范式为 m00 m01 m11 (P Q) (P Q) (P Q) (3 分)
a b
c
e
d
f
g
(答案不唯一)(6 分)评分细则:每画错一个结点扣 1 分,直到扣为 0 分止。若树高度画错此题记为 0 分。
a 对应的前缀码为:00
b 对应的前缀码为:10
c 对应的前缀码为:010
d 对应的前缀码为:111
e 对应的前缀码为:011
f 对应的前缀码为:1100 g 对应的前缀码为:1101
七、(10 分)Q 为有理数集,设*为定义在 Q 上的运算 a*b=a+b-4 1).*在 Q 上可结合吗?*在 Q 上可交换吗? 2).求 Q 中关于运算*的幺元。 3).集合 Q 上所有的元素都有逆元吗?若有逆元,请求出。
解: 1).对于 Q 中的任意元素 a,b,c ,(a*b)*c=(a+b-4)*c= a+b-4+c-4=a+b+c-8=a*(b*c) ,所以*在 Q 上可结合。(2 分) 因为 a*b=a+b-4=b*a 所以*在 Q 上可交换。(2 分) 2)设 e 为所求的幺元,则对于任意的 a∈Q 有 a*e=e*a=a =a+e-4 解得 e=4 ,所以 Q 中关于运算*的幺元为 4。(3 分) 3)任取 a∈Q,有 8-a∈Q, 而 a*(8-a)=a+(8-a)-4=4
(4 分)
山东理工大学《离散数学》试卷纸
共 3 页 第1 页
(A)卷
第 2007-2008 学年第 二 学期
班级:
姓名:
学号:
…………………………………装……………………………订…………………………线………….………………………………
五、简答题(10 分) 设集合 A={1,3,4,5,6,12,24},D 为 A 上的整除关系,则 (1).〈A ,D 〉是偏序集吗? (2).写出集合{3,4,6,12}的上确界、下确界、极大元、极小元、最大元、最小元。
适用专业 计算机科学与技术
题号
一
二
三
得分
评阅人
复核人
考核性质 考试 闭 卷
四
五六 七
命题教师 张艳华 石少俭 考试时间 100 分钟
八
九
十 十一
总分
一、判断题:(对者划√, 错者划× 10 分)
1.如果 A B ,则有 A B 。(√ ) 2.设 R 与 S 是集合 A 上的任意两个关系。若 R 与 S 是反对称的,则 RoS 也是反对称的。(× )
八、(10 分)
1、(5 分)试画出一个无向图,它是欧拉图,但不是哈密尔顿图。
(5 分)(答案不唯一) 2、(5 分)求下图的最小生成树。(不写步骤)
4
2 13
2
12 11 5 6
8
9
7
9
10
(5 分) 评分细则:每画错一条边扣 1 分,直到扣为 0 分止。
13
56 8
九、(10 分)设在通信中 a,b,c,d,e,f,g 这 7 个字母,传输时出现的频率分别为 35%,20%,15%,9%,11%,5%,5%, 画出相应的最优二叉树,并写出每个字母对应的前缀码。
郑重声明: 该文档仅供本校学生考试参考所用
任何人不得用作其它商业用途 请下载完后于 24 小时内删除
本人不承担任何法律责任
山东理工大学《离散数学》答案及评分细则
( A)卷
第 2007-2008 学年第二 学期
班级:
姓名:
学号:
…………………………………装……………………………订…………………………线………….………………………………
(3 分)
2)对称:因为 <<x,y>,<u,v>>∈R xv=yu, uy=vx, 所以<<u,v>,<x,y>>∈R
(3 分)
)传递:因为如果<<x,y>,<u,v>>∈R , <<u,v>,<s,t>>∈R ,xv=yu,ut=vs,xvut=yuvs,xt=ys, 所以<<x,y>,<s,t>>∈R
3.(0,1,3,3,3)可以构成简单图的度数序列。( × )
4.如一个有向图是欧拉图,则此图一定是强连通图。此命题真值为真。( √ )
5.若〈S,*〉是一个阿贝尔群,则在关于运算*的运算表中任意两行或两列都是不相同的。( √ )
二、填空题:(每空 2 分 共 20 分)
1.将命题符号化。“凡偶数均能被 2 整除”。其中 F(x):x 是偶数。G(x):x 能被 2 整除。( x(F(x) G(x)) )。
2.已知集合 A={1,2},则 A 上可以定义( 16 )个不同的二元关系, A 的幂集为({{1},{2},{1,2}, } )。 3.设 M(x):x 是人,G(x):x 犯错误。则命题“没有不犯错误的人”形式化为( x(M (x) G(x)) )。
4.已知集合 A 和 B,|A|=3, |B|=4 则 A,B 间有( 64 )个函数;
答:(1).〈A ,D 〉是偏序集。(4 分) (2)集合{3,4,6,12}的上确界为 12、下确界为 1、极大元为 12、极小元为 3,4、最大元为 12、最小元无 (每个 1 分,共 6 分)
六、证明题:(10 分) 设<G,*>是群,对任一 aG,令 H={y|y*a=a*y,yG},试证明<H,*>是<G,*>的子群。 证明:显然 H G,运算*在 H 中满足结合性。 对于任意的 x,yH,以及任意的 aG,因为 (x*y)*a=x*y*a=x*a*y=a*x*y=a*(x*y) 所以 x*yH,运算*关于 H 是封闭的。 (5 分) 记 e 为 G 的幺元,因为 e*a=a*e,所以 eH 对于任意的 xH,由于 x*a=a*x,所以 x-1*(x*a)*x-1=x-1*(a*x)*x-1 即得 a*x-1=x-1*a 有 x-1 H 综上所述<H,*>是<G,*>的子群。 (5 分)
(8-a)*a=(8-a)+a-4=4 所以 Q 上任一的元素 a 都有逆元 8-a. .(3 分)
山东理工大学《离散数学》试卷纸
共3 页 第2 页
(A )卷
第 2007-2008 学年第 二 学期
班级:
姓名:
学号:
…………………………………装……………………………订…………………………线………….………………………………
5.若 G=<V, E>为 n 阶无向完全图,则每个结点的度数为(n-1 )。
6.若某连通平面图有 10 个结点,12 条边,r 个面,则 r=( 4 )。
7.在代数系统<I,+>中,-5 的逆元为( 5 ),33=( 9 ) 。
8.10 阶群的子群的阶数可能为(1,2,5,10 )
三、(10 分)试求 P ((P Q) (Q P)) 的主析取范式与主合取范式。
P ((P Q) (Q P)) 的主合取范式为 M10 P Q
(3 分)
四、(10 分). 设正整数的序偶集合 A,在 A 上定义二元关系 R 如下:
<<x,y>,<u,v>>∈R,当且仅当 xv=yu,
证明:R 是 A 上的等价关系。
பைடு நூலகம்证明:1)自反:因为 <x,y>∈A,xy=yx 所以<<x,y>,<x,y>>∈R
(4 分) 评分细则:每写错两个字母前缀码扣 1 分。
共 3页 第 3 页
解:方法一: P ((P Q) (Q P)) P ((P Q) (P Q)) P ((P (P Q)) (Q (P Q)))
P (P Q) (P P) (P Q) P Q M10 (4 分)
P ((P Q) (Q P)) 的主析取范式为 m00 m01 m11 (P Q) (P Q) (P Q) (3 分)
