1.3真实气体与范德华方程
考研必备物理化学核心知识点

第一章气体的pvT关系一、理想气体状态方程pV=(m/M)RT=nRT(1.1)或pVm=p(V/n)=RT(1.2)式中p、V、T及n的单位分别为P a 、m3、K及mol。
Vm=V/n称为气体的摩尔体积,其单位为m3〃mol。
R=8.314510J〃mol-1〃K-1称为摩尔气体常数。
此式适用于理想,近似于地适用于低压下的真实气体。
二、理想气体混合物1.理想气体混合物的状态方程(1.3)pV=nRT=(∑BBn)RTpV=mRT/Mmix(1.4)式中Mmix为混合物的摩尔质量,其可表示为Mmix def ∑BBy M B(1.5)Mmix=m/n=∑BBm/∑BBn(1.6)式中MB为混合物中某一种组分B的摩尔质量。
以上两式既适用于各种混合气体,也适用于液态或固态等均匀相混合系统平均摩尔质量的计算。
2.道尔顿定律pB=nBRT/V=yBp(1.7)P=∑BBp(1.8)理想气体混合物中某一种组分B的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。
而混合气体的总压即等于各组分单独存在于混合气体的温度、体积条件下产生压力的总和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
3.阿马加定律V B *=nBRT/p=yBV(1.9)V=∑VB*(1.10)VB*表示理想气体混合物中物质B 的分体积,等于纯气体B在混合物的温度及总压条件下所占有的体积。
理想气体混合物的体积具有加和性,在相同温度、压力下,混合后的总体积等于混合前各组分的体积之和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
三、临界参数每种液体都存在有一个特殊的温度,在该温度以上,无论加多大压力,都不可能使气体液化,我们把这个温度称为临界温度,以Tc 或tc表示。
我们将临界温度Tc时的饱和蒸气压称为临界压力,以pc表示。
在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积,以Vm,c 表示。
化工热力学1.3 气体的非理想性及状态方程

主讲教师:吕京宁
奇妙的P-V-T
论坛帖子:烧天然气的车友,你们发现天气热了之后,车 子更费气了吗?我的车在天气较凉的时候,每公里1毛2, 现在这天气,每公里1毛4了,这是为什么呢?我测试过了, 没有漏气跑气的地方,没开空调……
月球上为何没有液态的水? 最软的石墨能变成坚硬的金刚石吗?
1873年,Van der Waals的论文很快就受 到著名物理学家Maxwell的重视。Maxwell在 《自然》杂志上评述了 Van der Waals 的工 作,并且断言 “Van der Waals的名字将很 快出现在第一流分子科学家的名单中。”从 而使这位年轻人用荷兰文撰写的论文很快为 物理学界所知晓。
0
p
2 p
( V
)Tc
0, ( ቤተ መጻሕፍቲ ባይዱ 2 )Tc
0
把van der Waals方程代入上述条件,即可得
p
RT 2a
( V
)Tc
(Vc
b)2
Vc3
0
2 p ( V 2 )Tc
2RTc (Vc b)3
6a Vc4
0
b 1 RTc 8 Pc
a 27 R2Tc2 64 Pc
vdW常数常 用形式
一些气体的范德华参量
启迪与导航
van der Waals出身贫苦,中学时代一度辍学 在印刷厂当学徒工,后在小学和中学教书,由 于不懂古典语言失去报考大学资格。他以顽强 的自学精神感动了莱顿大学的教授们,而被破 例获准旁听课程和进实验室实验。 1873 年van der Waals获博士学位,其博士论文以 “论气态 和液态的连续性”为题将 van der Waals方程公 布于世。
实际气体的范德华方程是如何推导出来的

实际气体的范德华方程是如何推导出来的实际气体的范德华方程是描述气体行为的重要方程之一,它是由荷兰物理学家约翰·德·范德华于1873年提出的。
范德华方程是在理想气体状态方程的基础上进行修正和拓展的,可以更准确地描述实际气体的性质和行为。
在推导范德华方程之前,我们先简要回顾一下理想气体状态方程。
理想气体状态方程是描述气体行为的基本方程,它建立了气体的压力、体积和温度之间的关系。
根据理想气体状态方程,可以得到PV = nRT,其中P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的温度。
然而,理想气体状态方程假设气体分子之间没有相互作用力,忽略了分子之间的吸引力和斥力,因此只适用于低密度和高温的气体。
为了更准确地描述实际气体的行为,范德华引入了修正因子和吸引力势能的概念,提出了范德华方程。
范德华方程的推导基于气体分子之间的范德华力。
范德华力是一种分子间的吸引力,它是由于分子之间的瞬时诱导极化而产生的。
范德华力的大小与分子的极化程度和距离的六次方成反比。
在气体的高温和低密度条件下,范德华力对气体性质的影响非常小,可以忽略不计。
但在低温和高密度条件下,范德华力成为主导因素,需要进行修正。
为了修正理想气体状态方程,范德华引入了修正因子b和吸引力势能项an^2/V^2。
修正因子b考虑了气体分子体积对气体压力的影响,它是一个与分子数密度有关的常数。
吸引力势能项an^2/V^2考虑了范德华力对气体压力的修正,其中a是与气体分子之间相互作用力有关的常数。
将修正因子b和吸引力势能项an^2/V^2加入理想气体状态方程中,得到修正后的范德华方程:(P + an^2/V^2)(V - nb) = nRT。
范德华方程在描述实际气体的压力、体积和温度之间的关系时,考虑了分子间的吸引力和体积效应,能够更准确地预测气体的性质和行为。
范德华方程的推导过程涉及了一些复杂的物理和数学知识,包括分子间力的作用机制、统计力学的基本原理等。
普通化学第一章总结

弯曲液面的液体的蒸气压
液体的饱和蒸气压不仅与液体的温度有关,还与液体的压力有关。Ps=P外+ 。凹液面的蒸气压降低,凸液面的蒸气压减小。并且弯曲液面的饱和蒸汽压与平液面的饱和蒸汽压存在以下关系:
㏑ = 开尔文公式
M为液体的摩尔质量,
注意r的正负号。
与此类似的是稀溶液的凝固点降低的现象 Tf=Kf*mb.
1.6 液体的表面张力
表面张力:液体与气体的分界面上存在时液体表面积缩小的紧缩力,称为表面张力。
定义:
表面张力与液体本身的性质有关,与接触相的性质有关,还与环境中的温度、压力有关。例如降低温度,表面张力会升高。
弯曲液面上的表面张力
P= , 为液体的表面张力,r为液体的弯曲半径。并且,凹液面的曲率半径为正值;凸液面的曲率半径为负值。在毛细吸管中 ( 为接触角, 是毛细管的半径。
1.4水的相图
对OA段,OA表示水的饱和蒸汽压与温度的关系,曲线上的任意的一点都代表了液态的水与水蒸气两相平衡的状态;液态水合水蒸气的两相平衡状态都可以用曲线上的点来表示。注意:当温度高于Tc时,图像截止了,是因为此时水在超临界状态下,为流体。根据曲线OA 知,饱和蒸汽压越高(即液体受到的压力越大),液体的沸点越高。可以根据㏑Ps=— +B讨论,Ps与T成正比的关系。
真实气体的液化及临界参数

对应状态原理: 当不同气体有两个对比参数相等时,第三个对比
参数也将(大致)相等。
3. 普遍化压缩因子图
将对比参数引入压缩因子,有:
Z
pVm RT
pcVm,c RTc
prVr Tr
Zc
prVr Tr
Zc 近似为常数(Zc 0.26~0.29 ) 当pr , Vr , Tr 相同时,Z大致相同,
Z = f (Tr , pr ) 适用于所有真实气体
•
(0.035+0.025)×8.314×373.15
=
Pa
2.0×10-3
•
• =93.07kPa < 101.325kPa
• 所以H2O肯定为气态 • 定T,pB < pB*,B液体蒸发为气体至pB = pB*
2. 临界参数
由表1.3.1可知:p*=f (T) T ,p*
当T=Tc 时,液相消失,加压不再可使气体液化。 临界温度 (Tc或tc):使气体能够液化所允许的最高温度
Z
Vm ห้องสมุดไป่ตู้m
真实 理想
理想气体 Z=1 真实气体 Z < 1 : 比理想气体易压缩
Z > 1 : 比理想气体难压缩
在一定的T,p下,某真实气体的Vm,真实大于理想 气体的Vm,理想,则该气体的压缩因子Z()
a. >1 b. <1 c. =1 d. 无法判断
答案:a
临界点时的 Zc :
Zc
pcVm,c RTc
a. 气 b. 液 c. 气-液两相平衡 d. 无法确定其状 态
答案:a
3. 真实气体的 p-Vm 图及气体的液化
三个区域: T > Tc T < Tc T = Tc
真实气体的液化及临界参数
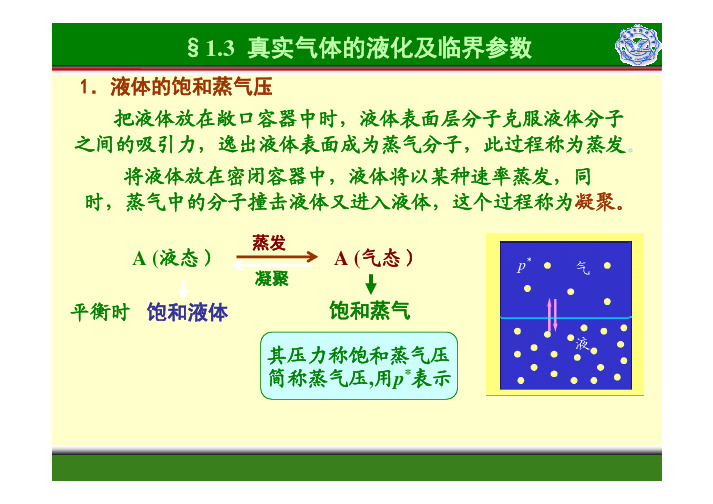
1.液体的饱和蒸气压苯乙醇水表不同温度的水、乙醇和苯的饱和蒸气压表不同温度的水、乙醇和苯的饱和蒸气压●同一物质,蒸气压随温度的升高而增大●大气中水蒸气的压力达到其饱和蒸气压时,称为相对湿度为100%2. 临界参数如图势能曲线所示,随着分子间距的缩小,分子间力将从吸引转为排物质的饱和蒸气压随温度的升高而急速增大,温度越高,使气体液化所一种纯气体的温度超过某一定值以后,靠加压来缩小分子间距使其液3. 真实气体的p-V图及气体的液化cm饱和曲线西安电子科技大学技大学图1.1.3真实气体的p-V m等温线技大学 技大学 技大学 西安电子科技大学西安电子科技大学西安电子科技大学超临界流体气和风味。
采用超临界流体技术脱除咖啡因,可避免以上缺点。
mm技大学 技大学西安电子科技大学西安电子科技大学9理想气体p V m /J ·m o l -1p V mp V m /J ·m o l -1m -p 图技大学 技大学 西安电子科技大学西安电子科技大学技大学 技大学 技大学 西安电子科技大学西安电子科技大学西安电子科技大学m <RT )范德华方程()a ⎛⎞技大学 技大学 技大学 西安电子科技大学西安电子科技大学西安电子科技大学★设分子A 、B 是半径为r 的圆球,当两个分子相碰时,质心间的最短距离x = 2r 。
★把分子B 看成是位于其球心处的质点,这个质点不能进入以分子A 为圆心、2r 为半径的球形禁区内,球形禁区的体积等于②b 是lmol 硬球气体分子本身体积的4倍★由于是两个分子碰撞,这个体积属于两个分子。
对每个分子来说,不能进入的体积为331444233x r ππ⎛⎞⎛⎞×=×⎜⎟⎜⎟⎝⎠⎝⎠即相当于分子本身体积的4倍。
3344(2)833r r ππ⎛⎞=×⎜⎟⎝⎠即等于分子本身体积的8倍。
技大学 技大学 西安电子科技大学西安电子科技大学27过饱和蒸汽过饱和液体方法,为以后建立更准确的真实气体状态方程,奠定了基础。
物理化学第一章讲义

第一章气体的pVT 关系§1.1 理想气体状态方程§1.2 理想气体混合物§1.3 真实气体的液化及临界参数§1.4 真实气体状态方程§1.5 对应状态原理及普遍化压缩因子图教学重点及难点教学重点1.理解理想气体模型、摩尔气体常数,掌握理想气体状态方程。
2.理解混合物的组成、理想气体状态方程对理想气体混合物的应用,掌握理想气体的分压定律和分体积定律。
3.了解气体的临界状态和气体的液化,理解液体的饱和蒸汽压。
4.了解真实气体的pV m - p图、范德华方程以及压缩因子和对应状态原理。
教学难点:1.理想气体的分压定律和分体积定律。
前言宏观的物质可分成三种不同的聚集状态:气态:气体则最为简单,最易用分子模型进行研究。
液态:液体的结构最复杂,对其认识还很不充分。
固态:结构较复杂,但粒子排布的规律性较强,对其研究已有了较大的进展。
当物质的量n确定后,其pVT 性质不可能同时独立取值,即三者之间存在着下式所示的函数关系:f(p,V, T)= 0也可表示为包含n在内的四变量函数式,即f(p,V,T,n)= 0这种函数关系称作状态方程。
§1-1 理想气体的状态方程1.理想气体状态方程(1)气体的基本实验定律:波义尔定律:PV = 常数(n,T 恒定)盖·吕萨克定律:V/T = 常数(n,p恒定)阿伏加德罗定律:V/n=常数(T,p恒定)( 2 ) 理想气体状态方程上述三经验定律相结合,可整理得理想气体状态方程:pV=nRT(p: Pa(帕斯卡)V: m3(米3) T:K(开尔文)R(摩尔气体常数): J·mol-1·K-1(焦·摩尔-1·开-1))因为摩尔体积V m = V/n,气体的物质的量n=m /M理想气体状态方程又常采用下列两种形式:p V m=RT、pV=(m/M)RT2.理想气体模型(1)分子间力:分为相互吸引和相互排斥,按照兰纳德一琼斯的理论:E=E吸引+E排斥=-A r6+B r12由图可知:[1]当两个分子相距较远时,它们之间几乎没有相互作用。
1-3真实气体状态方程

范德华方程只是一种简化的实际气体数学模型, 人们把在任何温 度压力下均服从范德Байду номын сангаас方程的气体称为范德华气体. 某些气体的范 德华常量可以从有关手册查到. 若实际气体压力趋于零, 则范德华方程还原为理想气体状态方程. 范德华方程在几 MPa(几十个大气压)的中压范围精度比理想气体 状态方程高, 但难以满足对高压气体计算的需要.
Z 的大小表示了实际气体难压缩的程度 描述了实际气体偏离理想气体行为的情况。 Z = f ( p 、T )
00-7-22 1
2. 范德华方程
2 ( p a / Vm 2 )(Vm b ) RT ( p a / Vm )(Vm b ) RT 2 2 或 ( p n 2 a / V 2 )(V nb ) nRT 或 ( p n a / V )(V nb ) nRT
§1-3 真实气体状态方程
1. 真实气体的与理想气体的偏差
RT Vm (理) p
pVm= RT
pVm≠ RT pVm = ZRT
压缩因子Z:
def pV pVm Vm (实) Z Vm (理 ) nRT RT
Z < 1 , Vm(实) < Vm(理),实际气体比理想气体易压缩; Z > 1 , Vm(实) > Vm(理),实际气体比理想气体难压缩; Z = 1 , Vm(实) = Vm(理),实际气体符合理想气体性质。
00-7-22
2
范德华气体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4/10/2014
4/10/2014
一些气体的范德华参量
4/10/2014
例题解析 计算结果表明,在低压和中压范围内(约为若干个MPa 以下),用范德华方程计算真实气体的pVT行为,可以得到 远远优于理想气体状态方程的结果。但对于更高的压力, 则用范德华方程计算也会带来较大偏差。这是因为范德华 假设的真实气体模型仍过于简单,而且实验表明,范德华 参量a,b之值并不能在很宽的温度、压力范围内保持不变。
2 m m 2 2
def m
以上即为著名的范德华方程。方程式中的a,b是气体的 pV 特性参量,称为范德华参量。它们分别与气体分子之间引力 Z RT 的大小及气体分子本身的体积大小有关。范德华认为,a和b 的值不随温度而变。下表给出了由实验测得的部分气体的范 德华参量之值。由表中数值可以看出,对于较易液化的气体, 如Cl2,SO2等,a的值较大,说明这些气体分子间的吸引力 较强;而对于如H2,He等不易液化的气体,a的值很小,说 明分子间的引力很弱。
4/10/2014
pVm RT
(i) 在pVm=RT方程式中,Vm是1mol气体分子自由活动的空 间。理想气体因为分子本身没有体积,则就等于容器 的体积。对于真实气体来说,因为要考虑分子本身的 体积,所以1mol气体分子自由活动的空间已不是Vm , 而要从Vm中减一个与气体分子本身体积有关的修正项b。 对1 mol气体而言:
1.3真实气体与范德华方程
1、真实气体对理想气体的偏差
为了定量描述真实气体的pVT行为与理想 气体的偏离程度,定义压缩因子Z为
pVm Z RT
def
pV Z 或 nRT
def
Vm Vm Z RT / p Vm ,id
式中,Vm为真实气体在某一确定状态下的摩尔体积, Vm,id 代表与真实气体具有相同温度和相同压力的理想气 体的摩尔体 1、低温低压:分子本身体积忽 略,分子间引力不忽略 2、高压:分子间距小,分子本 身体积不能忽略,分子间作用 力中斥力占主导 3、高温:分子热运动加剧,引 力作用可忽略,体积成为主导 因素 易压缩,Z<1
难压缩,Z>1
4/10/2014
范德华方程 为了能够比较准确地定量描述真实气体的 pVT行为,自19世纪以来,人们在大量实验的基 础上,提出了许多形式各异的真实气体状态方程, 它们的适用对象及精确程度也有所不同。 在众多的探索真实气体状态方程的科学家 中,荷兰科学家范德华(van der Waals J D)于1871 年首先从理论上建立了真实气体的微观模型,并 在此基础上对理想气体方程进行了修正,提出了 一个与实验结果比较一致的真实气体状态方程。 范德华提出:
实验表明,从数量级上看b的值粗略等于该气体物质 的液体的摩尔体积。
4/10/2014
• (ii)在pVm=RT方程中p是指分子间无引力时,气体分子 碰撞容器壁所产生的压力。但由于分子间引力的存 在,真实气体所产生的压力要比无引力时小。若真 实气体表现出来的压力为p,换算为没有引力时(作 为理想气体)的压力应该为p +a/Vm2。范德华把 a/Vm2项称为分子内压,它反映分子间引力对气体压 力所产生的影响。
式中a为一比例系数,它与真实气 体分子间的引力大小有关。
4/10/2014
经过两项修正,真实气体可看作理想气体加以处理。用 Vm-b代替理想气体状态方程中的Vm ,以p +a/Vm2代替方 程中的p,即得到范德华方程式:
p a / V (V b) RT 或 p n a / V (V nb) nRT
