LCL(LC)伯德图20110309
合集下载
5-3 频域:伯德图12

说明
为二阶系统 (振荡环节) 的转角角频率。
24
5.2.4 基本因子的伯德图
渐进线与实际曲线的误差与阻尼比ζ有关,当ζ< 0.707时必须考虑ζ对L(ω)的影响,对转角角频 率ω=ωn附近的L(ω)曲线进行修正。
当频率接近 ω=ωn时,将产生谐振峰。阻尼比的大 小决定了谐振峰值的幅值。
25
2ζ/n ω arctan 1 (/n ) 2
得到系统的对数幅频特性、相频特性。
9
5.2.3 对数频率特性图(伯德图)
典型环节归纳为四类基本因子:
常数增益K
在原点的极点(或零点) (jω)±1
实极点(或零点) ( jωτ +1)±1
复极点(或零点) [(jω/ω n )2+2ζ( jω/ω n ) +1]
±1
10
5.2.4 基本因子的伯德图
当 ω 1 / T 时,是一条斜率为-20dB/dec的直线
18
两条渐近线相交处的角频率 ω 1/ T 称为转角角频率。 用两条渐近线近似惯性环节的对数幅频特性,最大误差出现 在转角角频率处,
L( ) 20lg 1 ω 2 T 2
L ( )
1 / T
3 dB
L ( )
ω 90
20 0 0.1
20
1
10
20
( )
90
0
0.1
1
10
15
若在原点有多重零点 (jω)v
G jω ( jω) v
Lω 20lg G jω v 20lgω
ω v 90
16
3.实极点(或零点) (jωτ+1) ±1的伯德图
自动控制原理:第六章频域分析法——伯特图及稳定性分析

0.1
0.05
0.05
0.1 0.3
(1 T 2 2
j2T)1
0.7
1
1
10
/ n
(ω) arctan[(2ζωT)/ (1 ωT2 )] 相角:0°~-180°
6.4 系统开环频率特性-典型环节的伯德图特性:
令
dA ( ) d
0,得
谐振
20
10
Bode Diagram 转折频率
0 K 0
90
K 0 180
101
100
101
102
/(rad/sec)
6.4 系统开环频率特性-典型环节的伯德图
2) 积分环节( j )1,微分环节( j )
Bode Diagram 20
1 j
L() /(dB)
积分
A( ω ) 1 ,( ω ) 90
ω
0 j
20
微分 A(ω) ω,(ω) 90
6.3 频率特性图示法-对数幅相频率特性曲线
6.3.3 对数幅相特性曲线(尼科尔斯(N.B.Nichols)曲线)
横坐标为相位()
纵坐标为对数幅值L()=20lgA()
绘制过程:
0
L() /(dB)
从伯德图中分别读取各频率 10 下L()和()的值,
20
在尼科尔斯坐标系中确定相
应的点并将频率作为参变 30 量标于各点旁,
r n 1 2 2
A(r ) Am 2
1
1 2
L() /(dB)
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40
如何绘制伯德图PPT课件

G( j ) G1 ( j )G2 ( j )Gn ( j ) G( j ) G1 ( j ) G2 ( j ) Gn ( j ) L( ) 20 lg G( j) 20 lg G1 ( j) 20 lg G2 ( j ) 20 lg Gn ( j)
G( j ) 00
(5-63) (5-64)
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时,即
dB L()
G(
j
)
(
1
j
)n
其对数幅频特性为
20 lg
G(
j )
20 lg
1
பைடு நூலகம்n
40
( 5-70 )
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
(5-72) 度 ()
6
设 ' 10 ,则有
20lg ' 20lg 10 20 20lg
dB L()
可见,其对数幅频特性是一条在
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线 (ω 轴),且以每增加十倍频降 低20分贝的速度(-20dB/dec ) 变化的直线。
40
20dB / dec
1
L() dB
G( j ) 00
(5-63) (5-64)
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时,即
dB L()
G(
j
)
(
1
j
)n
其对数幅频特性为
20 lg
G(
j )
20 lg
1
பைடு நூலகம்n
40
( 5-70 )
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
(5-72) 度 ()
6
设 ' 10 ,则有
20lg ' 20lg 10 20 20lg
dB L()
可见,其对数幅频特性是一条在
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线 (ω 轴),且以每增加十倍频降 低20分贝的速度(-20dB/dec ) 变化的直线。
40
20dB / dec
1
L() dB
控制系统的伯德图分析自动控制原理-理论篇第6节

PM ( c ) (180 ) 180 ( c )
c — 剪切频率,截止频率,增益穿越频率。
G(jc )H (jc ) 1 L(jc ) 0
增益裕量—Gain Margin(GM) 1 GM K g G(jg )H (jg )
GM b 20 lg G(jg )H (jg ) K gb
自动化工程学院自动控制原理课程组制
2015年11月
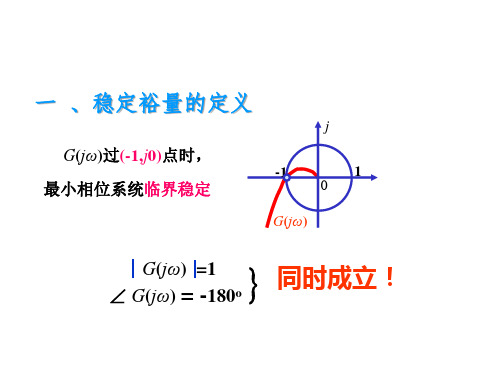
一 、稳定裕量的定义
j
G(jω)过(-1,j0)点时, 最小相位系统临界稳定
-1
G(jω)
0
1
G(jω) =1 ∠ G(jω) = -180o
同时成立!
K G(jωg) =1
G(jωg) -1 γ
ωg
∠G(jωc) – γ = –180o
幅值裕量 K=
K ( j ) 2 (Tj 1)
2 2
L ( ) 20 lg K 40 lg 20 lg T 1 0时有低频渐近线方程
L ( ) 20 lg K 40 lg 20 lg K a 40 lg
斜率=-40 db/dec,交点: 1 Ka L () T -40db/dec 1 T
0时有低频渐近线方程
20lgKp
L ( ) 20 lg K 20 lg K p
斜率=0, 与实轴无交点。
1 T
(2) N=1 (1型系统) G ( j ) H ( j )
K j (Tj 1)
2 2
L ( ) 20 lg K 20 lg 20 lg T 1 0时有低频渐近线方程
1 Kg
-180 不稳定闭环系统的GM和PM
典型环节的伯特图

3
5.1频率特性及其表示法 5.1.1 频率特性的基本概念
频率特性又称频率响应,它是系统(或元件)对不同频 率正弦输入信号的响应特性。
2 1.5 1
2 5 4 3
0.5 0 -0.5 -1
线性系统
1 0 -1 -2 -3
-1.5 -2
-4
0
0.5
1
1.5
2
2.5
3
-5
0
0.5
1
1.5
2
2.5
3
输出的振幅和相位一般均不同于输入量, 且随着输入信号频率的变化而变化
ห้องสมุดไป่ตู้s
微分 方程
p
d p dt
传递 函数
系统
频率 特性
s j
13
5.1.2 频率特性的表示法
(1)对数坐标图 (Bode diagram or logarithmic plot) (2)极坐标图 (Polar plot) (3)对数幅相图 (Log-magnitude versus phase plot) 对数幅频特性 对数频率 特性曲线 相频特性 纵坐标均按线性分度 横坐标是角速率 按 lg 分度 10倍频程,用dec
23
Asymptote 渐近线
0 -5
Corner frequency
Bode Diagram of G(jw )=1/(jw T+1) T=0.1
Asymptote 渐近线
Magnitude (dB)
-10 -15 -20 -25 0
精确曲线
Exact curve
Phase (deg)
精确曲线
-45
一阶因子 (1 jT ) 1
伯德莱蒙斜率法

伯德莱蒙斜率法
伯德图,也称波特图,指对数频率特性曲线(Bode diagram),其横坐标采用对数分度。
Bode图是经过处理的幅频特性图,普通的幅频率特性图,横坐标是频率,纵坐标是幅值的放大倍数,表明了一个电路网络对不同频率信号的放大能力。
但是在电子电路中,这种图有可能比较麻烦,一方面,要表示一个网络在低频和高频下的所有情况,那么横轴(频率轴会很长)。
此外,一般放大电路的放大倍数可能达到几百,使得纵轴也很长。
第三,这样画出的图形往往是很不规则的曲线。
波特(Bode)图是根据上述三点作了改进:
1,横坐标的频率改成指数增长,而不是以前的线性增长,比如频率刻度为。
10、100、1000、10^4、等,每一小格代表不同的频率跨度。
使一条横轴能表示如1hz到10^8hz这么大的频率范围。
2,纵坐标表示放大倍数的自然对数的20倍,这是根据分贝的定义做的。
这样纵坐标的值大概0到60就足够了。
这样在图中一眼就能看出放大的分贝数。
相频特性也可以相应的画。
3,把曲线做直线化处理。
画图所依据的式子中会得到fLfH的数值。
得出的波特图也应该在fL和fH处出现拐角(不是拐弯),尽管这点按拐角处理会产生一定的误差。
在斜率不为0的直线处要标明斜率。
标明出每十倍频程放大倍数的变化情况。
控制系统的伯德图分析——自动控制原理
() 0
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM,PM常作为控制系统的频域设计指标。
GM,PM大表明相对稳定性好,但响应速度低。 GM,PM小表明相对稳定性差,但响应速度高。 过大或过小都不好,较好的经验值为:
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0, 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec,交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec,交点: =Kv
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM,PM常作为控制系统的频域设计指标。
GM,PM大表明相对稳定性好,但响应速度低。 GM,PM小表明相对稳定性差,但响应速度高。 过大或过小都不好,较好的经验值为:
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0, 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec,交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec,交点: =Kv
伯德图分析-稳定性-及幅值和相角裕度

从根轨迹得到证实, 系统是条件稳定 的。
当k<k1时, 系统是不稳定的;
当k>k1时, 系统是不稳定的。
Im
K=K1
K=1
Re -2
2 zeroes
3 poles
图.16.13 系统的根轨迹图
通过伯德图判断稳定性的可靠方法是: - 如果系统有正的相角裕度,那么系统是
稳定的。
- 相角裕度是由伯德图判定系统稳定性的 唯一可靠的方法。
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
M ( pc)
g c
(g c)
(g c)
GMKc K
1
Mpc
P M180gc
GM db20lgM1 pc 20lgMpc
条件稳定
• 改变增益的作用是使幅值曲线上下平 移,而相角曲线不变。
如果 那么
2l0g KKd B
20lg2K20lg 220lgKKd B6
20lg0.5K20lg0.520lgKKd B6
• 考虑下面的例子:
K=0.1
Gs H s12sK 13s
转折频率为 1, 0.5, 0.34
• 奈奎斯特稳定性判据:
当相角为-180o时,如果系统幅值小于或等 于1,那么这个系统是稳定的。
在伯德图中, 单位幅值对应于 MdB=0。 例子中: 相位为-180°时, 幅值约为 – 18dB ,因此系统是稳定的。
获得最大值 Kmax=NK
1 1 2 0 l o g 1 0 N N 3 . 5 5 K 4 5 3 . 5 5 1 6 0
用劳斯阵列来验证结果: 特征方程为
( s 2 ) ( s 3 ) 2 K s 3 8 s 2 2 1 s 1 8 K 0
