实验2 离散时间傅里叶变换
数字信号处理____第二章 离散时间傅里叶变换(DTFT)

DTFT [ x ( n )]
)
1 2
[ X (e
j
) X (e
j
j
n
x (n )e
j n
[
n
x (n )e
j n
] [
*
n
x (n )e
j( )n
]
X (e
*
j
)
满足共轭对称性 共轭反对称函数
x a (t ) X a ( s )
§2.1 三大变换之间的关系
即:
X (z)
ze
sT
X (e
sT
ˆ (s) ) X a
取样信号
ˆ (s) ˆ a (t ) X x a
ˆ (s) X a
ˆ a (t )e x
st
dt
st
x ( n ) x a ( nT )
ˆ (s) 1 X a T
§2.1 三大变换之间的关系
k
X a ( s jk s )
令s=jΩ
ˆ ( j ) X ( e X a
j T
)
1 T
k
X a ( j jk s )
X (e
j
)
1 T
k
X a( j
k 2
d
11
X (e
j
)e
j n
d
非周期离散
12
2
§2.2 离散时间傅里叶变换(DTFT)
实验二用DFT及FFT进行谱分析

实验二用DFT及FFT进行谱分析实验二将使用DFT(离散傅里叶变换)和FFT(快速傅里叶变换)进行谱分析。
在谱分析中,我们将探索如何将时域信号转换为频域信号,并观察信号的频谱特征。
首先,我们需要了解DFT和FFT的基本概念。
DFT是一种将时域信号分解为频域信号的数学方法。
它将一个离散时间序列的N个样本转换为具有N个频率点的频率谱。
DFT在信号处理和谱分析中被广泛应用,但它的计算复杂度为O(N^2)。
为了解决DFT的计算复杂度问题,Cooley和Tukey提出了FFT算法,它是一种使用分治策略的快速计算DFT的方法。
FFT算法的计算复杂度为O(NlogN),使得谱分析在实际应用中更加可行。
在实验中,我们将使用Python编程语言和NumPy库来实现DFT和FFT,并进行信号的谱分析。
首先,我们需要生成一个具有不同频率成分的合成信号。
我们可以使用NumPy的arange函数生成一组时间点,然后使用sin函数生成不同频率的正弦波信号。
接下来,我们将实现DFT函数。
DFT将时域信号作为输入,并返回频域信号。
DFT的公式可以表示为:X(k) = Σ(x(n) * exp(-i*2πkn/N))其中,X(k)是频域信号的第k个频率点,x(n)是时域信号的第n个样本,N是信号的长度。
我们将使用循环计算DFT,但这种方法的计算复杂度为O(N^2)。
因此,我们将在实验过程中进行一些优化。
接下来,我们将实现FFT函数。
FFT函数将时域信号作为输入,并返回频域信号。
可以使用Cooley-Tukey的分治算法来快速计算FFT。
FFT的基本思想是将一个长度为N的信号分解为两个长度为N/2的子信号,然后逐步地将子信号分解为更小的子信号。
最后,将所有子信号重新组合以得到频域信号。
实验中,我们将使用递归的方式实现FFT算法。
首先,我们将信号分解为两个子信号,然后对每个子信号进行FFT计算。
最后,将两个子信号的FFT结果重新组合以得到频域信号。
离散时间傅里叶变换.

第3章 离散时间傅里叶变换在信号与系统中,分析连续时间信号可以采用时域分析方法和频域分析方法,它们之间是通过连续时间的傅里叶变换来完成从时域到频域的变换,它们之间是完成了一种域的变换,从而拓宽了分析连续时间信号的途径。
与连续时间系统的分析类似,在离散时间系统中,也可以采用离散傅里叶变换,将时间域信号转换到频率域进行分析,这样,不但可以得到离散时间信号的频谱,而且也可以使离散时间信号的分析方法更具有多元化。
本章将介绍离散时间系统的频域分析方法。
3.1 非周期序列的傅里叶变换及性质3.1.1 非周期序列傅里叶变换1.定义一个离散时间非周期信号与其频谱之间的关系,可用序列的傅里叶变换来表示。
若设离散时间非周期信号为序列)(n x ,则序列)(n x 的傅里叶变换(DTFT)为:正变换: ∑∞-∞=ω-ω==n nj j en x e X n x DTFT )()()]([ (3-1-1)反变换: ⎰ππ-ωωω-ωπ==d e e X n x e X DTFT n j j j )(21)()]([1 (3-1-2)记为:)()(ω−→←j Fe X n x当然式(3-1-2)等式右端的积分区间可以是)2,0(π或其它任何一个周期。
[例3-1] 设序列)(n x 的波形如图3-1所示,求)(n x 的傅里叶变换)(ωj e X 解:由定义式(3-1-1)可得ωω=--=--===ω-ω-ωω-ω-ωω-ω-ω-ω-=ω-∞-∞=ω∑∑21sin 3sin )()(11)()(25212121333656j j j j j j j j j nj n nj n j ee e e e e e e e een R e X 2.离散时间序列傅里叶变换存在的条件:图3-1离散时间序列)(n x 的傅里叶变换存在且连续的条件为)(n x 满足绝对可和。
即:∞<∑∞-∞=)(n x n (3-1-3)反之,序列的傅里叶变换存在且连续,则序列一定是绝对可和的。
离散时间傅里叶变换
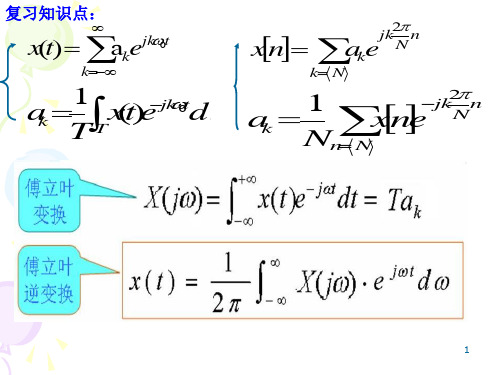
X
(e
j
)
sin
N1
sin
1 2
2
连续时间非周期矩形脉冲傅里叶变换: X(j)2sinT1
4. x[n][n]
X(ej) 1
Xej xnejn nejn1
n
n
20
三、离散时间傅里叶变换的收敛性
例5.1,5.2是无限长序列
x[n]a|n|,|a|1; 其傅里叶变换存在。 x[n]anu[n]|,a|1
X * ( e j ) X ( e j )即,X * ( e j ) X ( e j )
因此:
X (ej)X (e j) RX ( e ej) RX ( e e j) X (ej) X (e j) Im X (ej) Im X (e j)
❖ 若 x[n] 是实偶信号,则 x[n]x[n],
x% [n]X(ej)
ak2(k02l) kN l
23
如图P263 Fig5.9:下页
X (e j ) 2 a 0 ( 2 l) 2 a 1 (0 2 l)
l
l
.. .2aN1 ((N1)02l) ,02/N l
如果周期函数中包含连续相继的N次谐波,则有:
X(ej)2k ak(2N k)
调制特性在信息传输中是极其重要的。
一定是以 2 为周期的,因此,频域的冲激应该是周
期性的冲激串:
2(0 2k)
k
对其作反变换有
xn 1 X ej ejnd
2 2
0 ejnd ej0n
2
22
可见, 2( 02k) F 1 ej0n k
由DFS ,有 ~ xnkNakejk0n,02N
因此,周期信号 ~xn 可表示为DTFT
实验2 离散时间傅里叶变换

电 子 科 技 大 学实 验 报 告学生:项阳 学 号: 2010231060011 指导教师:邓建一、实验项目名称:离散时间傅里叶变换二、实验目的:熟悉序列的傅立叶变换、傅立叶变换的性质、连续信号经理想采样后进行重建,加深对时域采样定理的理解。
三、实验容:1. 求下列序列的离散时间傅里叶变换(a) ()(0.5)()n x n u n = (b) (){1,2,3,4,5}x n =2. 设/3()(0.9),010,j n x n e n π=≤≤画出()j X e ω并观察其周期性。
3. 设()(0.9),1010,n x n n =--≤≤画出()j X e ω并观察其共轭对称性。
4. 验证离散时间傅里叶变换的线性、时移、频移、反转(翻褶)性质。
5. 已知连续时间信号为t a e t x 1000)(-=,求:(a) )(t x a 的傅里叶变换)(Ωj X a ;(b) 采样频率为5000Hz ,绘出1()j X e ω,用理想插函数sinc()x 重建)(t x a ,并对结果进行讨论;(c) 采样频率为1000Hz ,绘出2()j X e ω,用理想插函数sinc()x 重建)(t x a ,并对结果进行讨论。
四、实验原理:1. 离散时间傅里叶变换(DTFT)的定义:2.周期性:()j X e ϖ是周期为2π的函数(2)()()j j X e X e ϖϖπ+= 3.对称性:对于实值序列()x n ,()j X e ϖ是共轭对称函数。
*()()Re[()]Re[()]Im[()]Im[()]()()()()j j j j j j j j j j X e X e X e X e X e X e X e X e X e X e ϖϖϖϖϖϖϖϖϖϖ-----===-=∠=-∠4.线性:对于任何12,,(),()x n x n αβ,有1212[()()][()][()]F x n x n F x n F x n αβαβ+=+5.时移[()][()]()j k j j k F x n k F x n e X e e ωωω---==6.频移00()[()]()j n j F x n e X e ωωω-=7.反转(翻褶)[()]()j F x n X e ω--=[()]()()(),()j j jn z e n n F x n X e X z x n e x n ωωω∞-==-∞∞=-∞===<∞∑∑收敛条件为:五、实验器材(设备、元器件):PC机、Windows XP、MatLab 7.1六、实验步骤:本实验要求学生运用MATLAB编程产生一些基本的离散时间信号,并通过MATLAB的几种绘图指令画出这些图形,以加深对相关教学容的理解,同时也通过这些简单的函数练习了MATLAB的使用。
离散时间傅里叶变换

离散时间傅⾥叶变换1. 离散时间傅⾥叶变换的导出针对离散时间⾮周期序列,为了建⽴它的傅⾥叶变换表⽰,我们将采⽤与连续情况下完全类似的步骤进⾏。
考虑某⼀序列x[n],它具有有限持续期;也就是说,对于某个整数N1和N2,在 −N1⩽以外,x[n]=0。
下图给出了这种类型的⼀个信号。
由这个⾮周期信号可以构成⼀个周期序列\tilde x[n],使x[n]就是\tilde x[n]的⼀个周期。
随着N的增⼤,x[n]就在⼀个更长的时间间隔内与\tilde x[n]相⼀致。
⽽当N\to \infty,对任意有限时间值n⽽⾔,有\tilde x[n]=x[n]。
现在我们来考虑⼀下\tilde x[n]的傅⾥叶级数表⽰式\tag{1}\tilde x[n] = \sum_{k=(N)}a_ke^{jk{(2\pi/N)}n}\tag{2}a_k = \frac{1}{N} \sum_{n=(N)} \tilde x[n]e^{-jk{(2\pi/N)}n}因为在-N_1 \leqslant N \leqslant N_2区间的⼀个周期上\tilde x[n]=x[n],因此我们将上式的求和区间就选在这个周期上\tag{3}a_k = \frac{1}{N} \sum_{n=-N_1}^{N_2} x[n]e^{-jk{(2\pi/N)}n} = \frac{1}{N} \sum_{n=-\infty}^{+\infty} x[n]e^{-jk{(2\pi/N)}n}现定义函数\tag{4}X(e^{j\omega})=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}可见这些系数a_k正⽐于X(e^{j\omega})的各样本值,即\tag{5}a_k = \frac{1}{N}X(e^{jk\omega_0})式中,\omega_0=2\pi/N⽤来记作在频域中的样本间隔。
离散时间信号的傅里叶变换和离散傅里叶变换

离散时间信号的傅里叶变换和离散傅里叶变换摘要本文主要介绍了离散时间信号的离散时间傅里叶变换及离散傅里叶变换,说明其在频域的具体表示和分析,并通过定义的方法和矩阵形式的表示来给出其具体的计算方法。
同时还介绍了与离散时间傅里叶变换(DTFT )和离散傅里叶变换(DFT )相关的线性卷积与圆周卷积,并讲述它们之间的联系,从而给出了用圆周卷积计算线性卷积的方法,即用离散傅里叶变换实现线性卷积。
1. 离散时间傅里叶变换1.1离散时间傅里叶变换及其逆变换离散时间傅里叶变换为离散时间序列x[n]的傅里叶变换,是以复指数序列{}的序列来表示的(可对应于三角函数序列),相当于傅里叶级数的展n j e ω-开,为离散时间信号和线性时不变系统提供了一种频域表示,其中是实频率ω变量。
时间序列x[n]的离散时间傅里叶变换定义如下:)(ωj e X (1.1)∑∞-∞=-=nnj j e n x e X ωω][)(通常是实变量的复数函数同时也是周期为的周期函数,并且)(ωj e X ωπ2的幅度函数和实部是的偶函数,而其相位函数和虚部是的奇函数。
)(ωj e X ωω这是由于:(1.2))()()(tan )()()()(sin )()()(cos )()(222ωωωωωωωωωωθωθωθj re j im j im j re j j j im j j re e X e X e X e X e X e X e X e X e X =+===由于式(1.1)中的傅里叶系数x[n]可以用下面给出的傅里叶积分从中算出:)(ωj e X 1(1.3)ωπωππωd e eX n x n j j )(21][⎰-=故可以称该式为离散时间傅里叶逆变换(IDTFT ),则式(1.1)和(1.3)构成了序列x[n]的离散时间傅里叶变换对。
上述定义给出了计算DTFT 的方法,对于大多数时间序列其DTFT 可以用收敛的几何级数形式表示,例如序列x[n]=,此时其傅里叶变换可以写成简单n α的封闭形式。
离散时间序列的傅里叶变换

傅里叶变换: 傅里叶反变换:
F ( j ) f ( t )e jt dt
1 f (t ) 2
F ( j )e jt d
一、离散序列傅里叶变换DTFT公式
F (e j ) F ( z )
T
z e jT
F (e j )
围内。
四、几种特殊的离散时间系统:
低通、高通、带通、带阻
全通系统
最小相位系统 最小相位系统:极零点全部在单位圆内。
全通
1) m=n;
2)
H (e j ) H 0 H ( z) |z 1
全通系统:对任意频率的离散正弦时间信号都有相同的幅
频响应,除了在z=0处的极点外,其余的极点和零点关于单
r (k )
i
k i k h ( i )( 1 ) ( 1 )
i
( 1) k H ( z ) z 1
H(-1)=32/3
32 r (k ) ( 1) k 3
k
作业:8.17 (2) , (3);
8.18(1)(5)
解:
F (e )
j
k
R
N
(k )e
j k
e jk
k 0
N 1
1 e 1 e j
j N
N sin j N 1 2 e 2 sin 2
| F (e j ) | e j ( )
|F(e j)| 幅频特性曲线 ()相频特性曲线
位圆镜像对称(即两者相角相等,幅度互为倒数, 或 zi
1 pi*
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电 子 科 技 大 学实 验 报 告学生姓名:项阳 学 号: 2010231060011 指导教师:邓建一、实验项目名称:离散时间傅里叶变换二、实验目的:熟悉序列的傅立叶变换、傅立叶变换的性质、连续信号经理想采样后进行重建,加深对时域采样定理的理解。
三、实验内容:1. 求下列序列的离散时间傅里叶变换(a) ()(0.5)()n x n u n = (b) (){1,2,3,4,5}x n =2. 设/3()(0.9),010,j n x n e n π=≤≤画出()j X e ω并观察其周期性。
3. 设()(0.9),1010,n x n n =--≤≤画出()j X e ω并观察其共轭对称性。
4. 验证离散时间傅里叶变换的线性、时移、频移、反转(翻褶)性质。
5. 已知连续时间信号为t a e t x 1000)(-=,求:(a) )(t x a 的傅里叶变换)(Ωj X a ;(b) 采样频率为5000Hz ,绘出1()j X e ω,用理想内插函数sinc()x 重建)(t x a ,并对结果进行讨论;(c) 采样频率为1000Hz ,绘出2()j X e ω,用理想内插函数sinc()x 重建)(t x a ,并对结果进行讨论。
四、实验原理:1. 离散时间傅里叶变换(DTFT)的定义:2.周期性:()j X e ϖ是周期为2π的函数(2)()()j j X e X e ϖϖπ+=3.对称性:对于实值序列()x n ,()j X e ϖ是共轭对称函数。
*()()Re[()]Re[()]Im[()]Im[()]()()()()j j j j j j j j j j X e X e X e X e X e X e X e X e X e X e ϖϖϖϖϖϖϖϖϖϖ-----===-=∠=-∠4.线性:对于任何12,,(),()x n x n αβ,有1212[()()][()][()]F x n x n F x n F x n αβαβ+=+5.时移[()][()]()j k j j k F x n k F x n e X e e ωωω---==6.频移00()[()]()j n j F x n e X e ωωω-=7.反转(翻褶)[()]()j F x n X e ω--=五、实验器材(设备、元器件):PC 机、Windows XP 、MatLab 7.1六、实验步骤:本实验要求学生运用MATLAB 编程产生一些基本的离散时间信号,并通过MATLAB 的几种绘图指令画出这些图形,以加深对相关教学内容的理解,同时也通过这些简单的函数练习了MATLAB 的使用。
[()]()()(),()j j jn z e n n F x n X e X z x n e x n ωωω∞-==-∞∞=-∞===<∞∑∑收敛条件为:七、实验源代码:1.(a)w = [0:1:500]*pi/500;x = exp(j*w) ./ (exp(j*w) - 0.5*ones(1,501));magx = abs(x);angx = angle(x);realx = real(x);imagx = imag(x);subplot(2,2,1);plot(w/pi,magx);gridxlabel('frequency in pi units');title('Magnitude Part');ylabel('Magnitude') subplot(2,2,3);plot(w/pi,angx);gridxlabel('frequency in pi units');title('Angle Part');ylabel('Radians')subplot(2,2,2);plot(w/pi,realx);gridxlabel('frequency in pi units');title('Real Part');ylabel('Real')subplot(2,2,4);plot(w/pi,imagx);gridxlabel('frequency in pi units');title('Imaginary Part');ylabel('Imaginary')1.(b)n = -1:3;x = 1:5;k = 0:500;w = (pi/500)*k;X = x * (exp(-j*pi/500)) .^ (n'*k);magX = abs(X);angX = angle(X);realX = real(X);imagX = imag(X);subplot(2,2,1);plot(k/500,magX);gridxlabel('frequency in pi units');title('magnitude Part')subplot(2,2,3);plot(k/500,angX);gridxlabel('frequency in pi units');title('Angle Part')subplot(2,2,2);plot(k/500,realX);gridxlabel('frequency in pi units');title('Real Part')subplot(2,2,4);plot(k/500,imagX);gridxlabel('frequency in pi units');title('Imaginary Part')2.n = 0:10; x = (0.9*exp(j*pi/3)).^n;k = -200:200;w = (pi/100)*k;X = x * (exp(-j*pi/100)) .^ (n'*k);magX = abs(X);angX = angle(X);subplot(2,1,1);plot(w/pi,magX);gridxlabel('frequency in units of pi');ylabel('|x|')title('Magnitude Part')subplot(2,1,2);plot(w/pi,angX/pi);gridxlabel('frequency in units of pi');ylabel('radians/pi') title('Angle Part')3.subplot(1,1,1)n = -5:5; x = (-0.9).^n;k = -200:200;w = (pi/100)*k;X = x * (exp(-j*pi/100)) .^ (n'*k);magX = abs(X);angX = angle(X);subplot(2,1,1);plot(w/pi,magX);gridaxis([-2,2,0,15])xlabel('frequency in units of pi');ylabel('|x|')title('Magnitude Part')subplot(2,1,2);plot(w/pi,angX/pi);gridaxis([-2,2,-1,1])xlabel('frequency in units of pi');ylabel('radians/pi') title('Angle Part')4.(1)x1 = rand(1,11);x2 = rand(1,11);n = 0:10;alpha = 2; beta = 3;k = 0:500;w = (pi/500)*k;X1 = x1 * (exp(-j*pi/500)).^(n'*k);X2 = x2 * (exp(-j*pi/500)).^(n'*k);x = alpha*x1 + beta*x2;X = x * (exp(-j*pi/500)).^(n'*k);X_check = alpha*X1 + beta*X2;error = max(abs(X - X_check))4.(2)x = rand(1,11);n = 0:10;k = 0:500;w = (pi/500)*k;X = x * (exp(-j*pi/500)).^(n'*k);y = x; m = n+2;Y = y * (exp(-j*pi/500)).^(m'*k);Y_check = (exp(-j*2).^w).*X;error = max(abs(Y - Y_check))4.(3)n = 0:100; x = cos(pi*n/2);k = -100:100;w = (pi/100)*k;X = x * (exp(-j*pi/100)) .^ (n'*k);y = exp(j*pi*n/4).*x;Y = y * (exp(-j*pi/100)) .^ (n'*k);subplot(1,1,1)subplot(2,2,1);plot(w/pi,abs(X));grid;axis([-1,1,0,60]) xlabel('frequency in units of pi');ylabel('|X|')title('Magnitude of X')subplot(2,2,2);plot(w/pi,angle(X)/pi);grid;axis([-1,1,-1,1]) xlabel('frequency in units of pi');ylabel('randiands/pi') title('Angle of X')subplot(2,2,3);plot(w/pi,abs(Y));grid;axis([-1,1,0,60]) xlabel('frequency in units of pi');ylabel('|Y|')title('Magnitude of Y')subplot(2,2,4);plot(w/pi,angle(Y)/pi);grid;axis([-1,1,-1,1]) xlabel('frequency in units of pi');ylabel('randiands/pi')title('Angle of Y')4.(4)n = -5:10; x = rand(1,length(n));k = -100:100;w = (pi/100)*k;X = x * (exp(-j*pi/100)) .^ (n'*k);y = fliplr(x);m = -fliplr(n);Y = y* (exp(-j*pi/100)).^(m'*k);Y_check = fliplr(X);error = max(abs(Y - Y_check))5.(a)Dt = 0.00005; t = -0.005:Dt:0.005;xa = exp(-1000*abs(t)); Wmax = 2*pi*2000;K =500; k = 0:1:K;W = k*Wmax/K; Xa = xa * exp(-j*t'*W)*Dt;Xa = real(Xa);W = [-fliplr(W),W(2:501)];Xa = [fliplr(Xa),Xa(2:501)];subplot(1,1,1)subplot(2,1,1);plot(t*1000,xa);xlabel('t in msec');ylabel('xa(t)')title('Analog Signakl')subplot(2,1,2);plot(W/(2*pi*1000),Xa*1000);xlabel('Frequency in KHz');ylabel('Xa(jW)'*1000)title('Continuous-tine Fouroer Transform')5.(b)(c)Dt = 0.00005; t = -0.005:Dt:0.005;xa = exp(-1000*abs(t)); Ts = 0.0002;n = -25:1:25;x = exp(-1000*abs(n*Ts));K =500; k = 0:1:K;w = pi*k/K;X = x * exp(-j*n'*w);X = real(X);w = [-fliplr(w),w(2:K+1)];X = [fliplr(X),X(2:K+1)];subplot(1,1,1)subplot(2,1,1);plot(t*1000,xa);xlabel('t in msec');ylabel('x1(n)')title('Discrete Signal');hold onstem(n*Ts*1000,x);gtext('Ts=0.2 msec');hold offsubplot(2,1,2);plot(w/pi,X);xlabel('Frequency in pi units');ylabel('X1(w)')title('Discrete-time Fourier Transform')八、实验数据及结果分析:2.1.a2.22.42.5bc九、实验结论:离散时间傅里叶变换(DTFT,Discrete-time Fourier Transform)是傅里叶变换的一种。
