交通事故引起的排队长度及消散时间的估算
交通事件下排队车辆数和总延误计算模型研究

交通事件下排队车辆数和总延误计算模型研究董国华左友兰摘要:为描述交通事件后导致拥挤交通流中的排队现象,分析预测交通流的时空影响。
根据流量守恒定律和交通波波速公式,提出了排队车辆数和车辆总延误定量计算的一个新模型。
将事件后交通流的发展划分为三个时间阶段,推导出道路堵塞时各相应时间段交通变量动态计算公式。
同时分析了交通事件影响因素除了事件本身的严重性外,事件的清理时间是决定事件瓶颈处车辆排队第二位的影响因素;以及交通事件时空发展模型与事件自动检测两者之间相互影响、互为因果的关系。
最后用应用算例对该模型的有效性进行验证,结果表明,数据符合实际情况,排队车辆数随着事件持续时间增加呈分段线性变化,而所有排队车辆的总延误随着交通事件处理时间的增加呈二次平方变化。
此模型可作为交通管理控制部门对交通事件发生后制定合理救援措施的理论依据。
关键词:交通事件;影响因素;交通流;排队车辆数;总延误;模型分析TP399:A1 引言近年来,由于我国机动车越来越多,人、车、路等矛盾也越来越突出。
在高速道路上,交通事故、车辆故障、货物散落、大货车占道、修路养路、路边停车、流量激增等交通事件是造成偶发性交通拥堵的主要原因,尤其是在节假日,事件发生后导致车辆排队现象在交通运输系统中随处可见。
交通事件发生后,原交通流的车流量会发生改变,车流量的波动甚至会传播到其它相邻的道路上去。
因此,交通事件对交通流的定量影响一直是一个倍受各方关注的问题。
特别是事件发生后,排队车辆数和总延误随时间如何增长,与事件特性如交通流量、车道数、事件处理效率等有何关系,对交通流预测、事件预警以及交通管理和控制都有重大意义[1]。
国内外很多研究者一直致力于排队现象的分析和交通流参数预测。
上世纪70年代,日本Akaike提出的Akaike信息准则(Akaike Information Crite-na,AIO经过各国大量实践证明,对交通流的预测精度在70%-800/0。
地铁中事故疏散时间和预测客流选值的计算方法

地铁中事故疏散时间和预测客流选值的计算方法摘要:由于城市地面交通日益繁忙,近年来交通拥堵现象在全国各大城市中尤为突出。
为了有效缓解地面交通,方便人们出行,合理利用和开发城市地下资源,建设地铁工程被各大城市认为是解决这一突出问题的有效手段。
但是由于地铁主要以地下工程居多,在规划设计阶段,各种不利因素也成为地铁建设者必须面对和克服的难题。
比如,在地铁发生意外事故时,尽快疏散地铁内部人员至安全区域显得异常重要。
本文以广州市地铁七号官堂站客流预测数据为例,参照目前地铁设计规范和地铁设计防火规范征求意见稿中事故疏散时间公式,简要计算事故发生在最不利情况下人员从站内疏散至站外安全区域所用的数值计算方法。
关键词:事故疏散客流预测超高峰系数断面客流目前我国地铁建设的车站规模,在满足市民出行和与城市局部区域需要相结合外,尽可能的以缩小投资规模和合理运用地下空间为原则。
但是车站宽度受上下行列车既有宽度影响外,合理预测客流量对有效站台宽度和楼扶梯设置数量起着决定性作用。
规范中事故疏散时间公式1.1、按《地铁设计规范GB50157-2003》疏散时间计算疏散时间T=1+{(Q1+Q2)/0.9[A1(N-1)+A2B]}<6分钟式中:Q1:表示1列车乘客数,该数据在客流预测表中选取。
也有Q1采用一列车满载人数进行取值,但是本人觉得这样虽然整条线安全性较高,但是在接近起点站和终点站附近,客流较为稀少列车一般达不到满载情况,该取值往往与实际情况偏差较大,显得不太经济、合理。
Q2:站台上候车乘客及站台层工作人员数。
候车乘客人数一般在客流预测表中选取,工作人员数量按定值考虑,比如可按站台层工作人员10人进行取值。
A1:1m宽自动扶梯通过能力(人/min),按现行规范规定取值。
A2:1m宽人行步梯通过能力(人/min),按现行规范规定取值。
B:人行楼梯宽度(m),按现行规范规定取值。
N-自动扶梯台数,往往在疏散计算时,N的取值一般规定:上行扶梯继续上行疏散;下行扶梯考虑一台故障,其余下行扶梯逆转按上行扶梯考虑进行疏散。
排队长度
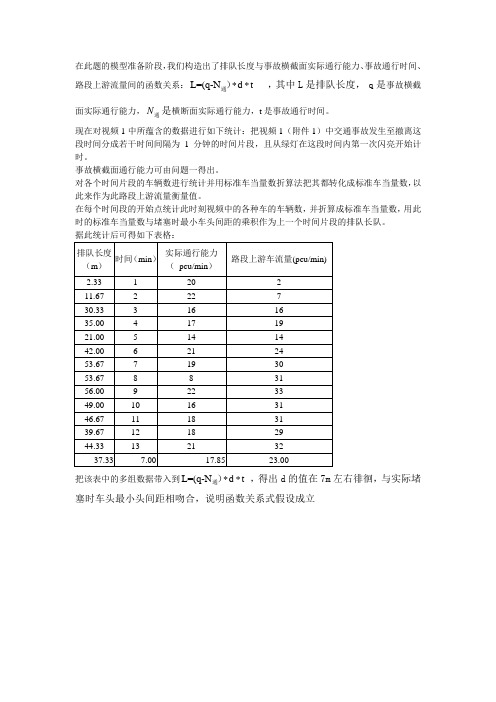
在此题的模型准备阶段,我们构造出了排队长度与事故横截面实际通行能力、事故通行时间、
路段上游流量间的函数关系:L=(q-N d t **通) ,其中L 是排队长度, q 是事故横截
面实际通行能力,N 通是横断面实际通行能力,t 是事故通行时间。
现在对视频1中所蕴含的数据进行如下统计:把视频1(附件1)中交通事故发生至撤离这段时间分成若干时间间隔为1分钟的时间片段,且从绿灯在这段时间内第一次闪亮开始计时。
事故横截面通行能力可由问题一得出。
对各个时间片段的车辆数进行统计并用标准车当量数折算法把其都转化成标准车当量数,以此来作为此路段上游流量衡量值。
在每个时间段的开始点统计此时刻视频中的各种车的车辆数,并折算成标准车当量数,用此时的标准车当量数与堵塞时最小车头间距的乘积作为上一个时间片段的排队长队。
据此统计后可得如下表格:
把该表中的多组数据带入到L=(q-N d t **通) ,得出d 的值在7m 左右徘徊,与实际堵
塞时车头最小头间距相吻合,说明函数关系式假设成立。
城市道路交通拥堵评价指标体系

城市道路交通拥堵评价指标体系城市道路交通拥堵评价指标体系是对城市道路交通拥堵程度进行评价和分析的一套指标体系。
该指标体系能够客观、全面地反映城市道路交通拥堵的程度和原因,为城市交通管理部门和决策者提供依据,帮助他们制定有效的交通拥堵缓解措施。
以下是一个常见的城市道路交通拥堵评价指标体系:1.交通流量:交通流量是指其中一段时间内通过一条道路或交叉口的车辆数量,通常以小时为单位。
交通流量的大小直接影响道路的通行能力和拥堵程度,因此是评价道路拥堵的重要指标之一2.交通速度:交通速度是指车辆在道路上行驶的速度,通常以公里/小时为单位。
交通速度的慢与快直接反映了交通流畅与拥堵的程度,因此是评价道路拥堵的重要指标之一3.延误指数:延误指数是指实际行驶时间与预计行驶时间之间的差距,通常用百分比表示。
延误指数是衡量道路交通拥堵程度的重要指标之一,可以直观地反映交通拥堵对车辆行驶速度的影响。
4.交通容量:交通容量是指道路在一定时间内所能容纳的最大交通流量。
交通容量的大小直接影响道路的拥堵程度,因此是评价道路拥堵的重要指标之一5.道路通行能力:道路通行能力是指其中一条道路在单位时间内能够容纳的交通流量。
道路通行能力的大小直接影响道路的拥堵程度,因此是评价道路拥堵的重要指标之一6.交通拥堵时长:交通拥堵时长是指道路在一段时间内处于拥堵状态的时间比例。
交通拥堵时长较长意味着道路拥堵问题较为严重,因此是评价道路拥堵的重要指标之一7.排队长度:排队长度是指在交通拥堵时,排在信号灯、交叉口或收费站等地点的车辆的长度。
排队长度的增加意味着道路拥堵程度加剧,因此是评价道路拥堵的重要指标之一8.交通事故率:交通事故率是指道路上发生交通事故的频率,可以用于评价道路交通拥堵的安全性。
交通事故率的增加可能与道路拥堵程度有关,因此是评价道路拥堵的重要指标之一9.环境污染:交通拥堵导致车辆长时间怠速和排放污染物,对环境造成一定的污染。
环境污染的程度可以通过测量大气污染物浓度、噪声水平等指标来评价。
浅谈事故路段道路的排队长度问题

L = L ( t )
路被占用 ,导致道路横断面通行 能力在单位
时间内出现 降低的现象,甚至 出现道路拥 堵 、瘫痪等严重现象 的发 生。本文通过参考
曲线决定系数 ( 一个 反应 因变量与 自变量相
关度大小的指标 ,其值越大 ,因变量与 自变
量的相关程度越大)R 2 _ 0 . 9 0 3 ,说明方程的 因变量与 自变量相关程度达到 9 0 . 3 %,且二 次方程的准确度 比一次方程和三次方程高 。 所 以,为了减小车辆排队长度 的计算误差, 建立 L关于 实际通行量 C p 的二次方程 Ⅲ,
S P S S 软件进行对次统计回归模 型进行汇总 与参数估计,并且得 出了车辆排队长度 L与 事故持续 时间 t 的回归曲线决定系数
R 2 = O . 9 3 3 ,说 明方程 的因变量与 自变量相关
程度达到 9 3 . 8 %,且三次方程 的准确度 比一
次方程和二次方程高。所 以,为了减小车辆 排 队长度 的计算误差,建立 L关于时间 t 的 三次方稗 “ ,即:
即: £ ( ) =c o + c + l c 2 c P
为了保证函数的准确性 ,我们再次利用
{ 2 0 1 3 高教社杯全国大学生数学建模竞赛
题 目》 , 运用 了其附件视频中所提供 的数据 , 简单分析了交通事故所影响的路段车辆 排 队长度与事故横断面实际通行能力和事 故 持续时间之间的关系 。
r e g r e s s i o n mo d e l i s e s t a b l i s h e d . Us i n g t h e r e g r e s s i o n c o e f i c i e n t , i t s i c o n c l u d e d t h a t t h e s t a t i s t i c a l r e re g s s i o n mo d e l p a r a me t e r s , he t mo d e l we r e e v a l u a t e d , a n d i t i s c o n c l u d e d t h a t t h e a f e c t e d b y h e枷 t c a c c i d e n t o f v e h i l c e q u e u e l e n g t h nd a he t r o a d a c c i d e n t c r o s s — s e c t i o n a l a c t u a l c a p a c i t y a n d he t r e l a t i o n s h i p b e t we e n t h e i n c i d e n t d u r a i t o n .
事故路段车辆排队长度分析

事故路段车辆排队长度分析
如下图所示,此路段长度总长480m,单方向车道数n为3,单方向车道宽度为D=3.25m,由视频1得发生事故的时间为16:42:32,设此时的时间为初始时间,即t=0,事故车辆占用道路为b(m)
长度为a(m),事故点上游路段长度为'L=240m。
假设车辆到达率为Q,在同级服务水平上事故发生断面通行能力为
Q,道路在正常条件
s
下的单方向通行能力为
Q。
i
视频1中交通事故位置示意图
此视频中的排队长度不同于以往文献的“排队长度”,这里的“阻塞行车道宽度”不只是事故车辆实际占用宽度,还包括虚拟占用宽度,比如事故发生位置横跨在两车道之间,导致事故点只能通行一个车道宽度的车流,那次此时“阻塞行车道宽度”为两个车道的宽度,视频1中占用的车道为第二、三车道。
2013年全国大学生数学建模竞赛A题:车辆排队长度与事故持续时间、道路实际通行能力、路段上流流量间的关系

道路上不断增加的交通流经常导致拥挤。
拥挤产生延误、降低流率、带来燃油损耗和负面的环境影响。
为了提高道路系统的效率,国内外许多研究者一直致力于车流运行模型的研究。
Daganzo[1]提出了一种和流体力学LWR 模型相一致的元胞传输模型,这种模型能用来模拟和预测交通流的时空演化,包括暂时的现象,如排队的形成、传播、和消散。
Heydecker 和Addison[2]通过研究车速和密度的因果关系分析和模拟了在变化的车速限制下的交通流。
Jennifer 和Sallissou[3]提出了一种混合宏观模型有效地描述了路网的交通流。
然而,拥挤也会由交通异常事件引起。
交通异常事件定义为影响道路通行能力的意外事件[4],如交通事故、车辆抛锚、落物、短期施工等,从广义角度看,还应包括恶劣天气与特殊勤务等。
异常事件往往造成局部车道阻塞或关闭,形成交通瓶颈,引起偶发性拥挤,这已经逐渐成为高速道路交通拥挤的主要原因[5],越来越多地受到研究者们的重视。
例如M. Baykal-Gursoy[6]等人提出了成批服务受干扰下的稳态M/M/c 排队系统模拟了发生异常事件的道路路段的交通流。
Chung[7]依据韩国高速公路系统监测的准确记录的大型交通事故数据库提出了一种事故持续时间预测模型。
当然,这些研究最终都是为了帮助缓解异常事件引起的交通拥挤。
交通异常事件发生后,事发地段通行能力减小,当交通需求大于事发段剩余通行能力时,车辆排队,产生延误,行程时间增加[8],交通流量发生变化。
本文以高速公路基本路段发生交通事故为例,主要分析了交通事故发生后不同时间段内事故点及其上游下游路段交通流量的变化,用于以后进一步的突发事件下交通流预测工作。
1 交通事故影响时间分析由于从交通事故发生到检测到事故、接警、事故现场勘测、处理、清理事故现场恢复交通,以及恢复交通后车辆排队不再增加都需要一定的时间。
这部分时间主要由三部分构成: 第一部分是事故发生到警察到达现场的时间T1; 第二部分是交通事故现场处理时间T2,由现场勘测、处理到事故族除、恢复交通; 第三部分是交通事故持续影响时间T3,这部分时间从恢复事故现场交通开始,到事故上游车辆排队不再增加,即排队开始减弱[9]。
交通事故引起的排队长度及消散时间的估算

交通事故引起的排队长度及消散时间的估算一、概述随着经济的快速发展和城市化进程的加快,交通问题日益成为制约城市可持续发展的重要因素之一。
交通事故作为交通问题的重要组成部分,不仅会造成人员伤亡和财产损失,还会引发交通拥堵,影响交通系统的正常运行。
对交通事故引起的排队长度及消散时间进行准确估算,对于有效应对交通拥堵、提高交通系统运行效率具有重要意义。
本文旨在探讨交通事故引起的排队长度及消散时间的估算方法。
通过对交通事故发生后的交通流特性进行分析,结合相关理论和模型,提出一套实用的估算方法。
该方法可以为交通管理部门提供决策支持,帮助他们在交通事故发生后迅速做出反应,采取有效措施减轻交通拥堵,提高道路通行能力。
同时,也可以为道路使用者提供有用的信息,帮助他们合理规划出行路线,避免拥堵区域,提高出行效率。
本文首先介绍了交通事故对交通流的影响,包括交通流量的减少、车速的降低等。
分析了影响交通事故排队长度和消散时间的因素,如事故发生的地点、时间、事故严重程度等。
接着,详细介绍了估算排队长度和消散时间的理论模型和计算方法。
通过案例分析,验证了所提估算方法的可行性和有效性。
通过本文的研究,可以为交通管理部门和道路使用者提供一套实用的估算方法,帮助他们更好地应对交通事故引起的交通拥堵问题,提高交通系统的运行效率和服务水平。
同时,也可以为未来的交通规划和管理提供有益的参考和借鉴。
1. 交通事故对道路交通的影响交通事故引起的排队长度取决于多个因素,包括事故发生的地点、时间、道路条件、交通流量等。
在高峰时段或交通瓶颈区域,事故更容易导致严重的交通拥堵和长时间的排队。
事故处理的时间和效率也会对排队长度产生影响。
如果事故处理及时、有效,排队长度可能会较短反之,如果处理缓慢或不当,排队长度可能会持续增长。
除了对交通流的直接干扰外,交通事故还可能对驾驶员和乘客的心理产生负面影响。
事故现场的混乱和不确定性可能导致驾驶员产生焦虑、紧张等情绪,进而影响他们的驾驶行为和安全性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下态车流密度: 状各出求可,系关的间者三量 mk/辆001=1。V/1S一lsK
2)1T—T(×Ⅱ.ⅣW+lT wⅡ.ⅢX(丁一%)
(6)
Ks2=&/V。—80辆/km mk/辆06—1,1/lO=1K
次本出解可)%一丁(×|)学墨_lh
。长队排的起引故事
2
系下的一队n辆车的运行状态变 化图。图中每条曲线表示一辆车运 行的时间一空间轨迹,车队密度不 同的两部分之间有一个分界面,虚 线OA是低密度状态向高密度状态 转变的分界面,它所体现的车流波 称为集结波;而BA是高密度状态 向低密度状态转变的分界面,它所 体现的车流波称为消散波。密度分 界面沿道路移动的速度称为波速, 在图中表现为虚线的斜率,其正负 号表示波传播的方向。从事故发生 至事故解除期间,上游车流由高速 低密的畅通状态转变为低速高密 的拥挤状态,从而形成集结波,波 面以一定的速度向车队的后方传 播;事故解除后,除了集结波继续 向车队后方传播外,在车队的前方 又形成了消散波,波面同样向车队 后方传播。当消散波的速度大于集 结波的速度时排队消散终能完成。 由车流波动理论可知,波速公 式为:
0
?
。F丢乡//j一
图1
—j乡/j
数
tj
车队运行状态变化图
图2车辆累计及消散过程图
万方数据
一聪5期
丁一墨二竺!二竺!×To
, 第27躐5固第 。尺一1K 卷第期■■
交通事故引起的排队长度及消散时间的估算 孔惠惠等 >、}匝 k 。 } 。劫/ 、∥彳t://, : 其中:‰爿茂抖卜警)| T/ 塑笋等等型一丁妣n血∥ 根据公式:x=w。.Ⅲ×(丁一死)= 图3车流波动传播图 时的行运车辆一示表线曲条每中图 纵,间时示表轴横。迹轨空一 持续时间7"0=15min,事故解除前
文章编号:1003—1421(2005)05—0065—03Βιβλιοθήκη 中图分类号:0226:U121
文献标识码:A
交通事故引起的排队长度及 消散时问的估算
Estimation of 0.ueue Length and Dispersing Time Caused by Traffic Accident
孔惠惠1,秦
42,China;3.Lanzhou Jiaotong
730070,China)
论对交通事故发生后的车流集结 摘 要:传统的排队论理论单纯使用需求量和通行能力关系推算 及消散过程进行分析,得出求解排 队长度和消散时间的估算方法。
1
排队长度,由于其未考虑车流波动的影响,从而使估算结果与实际 出入很大。现用车流波动理论分析发生交通事故后路段上车辆排 队的形成与消散过程,推导出估算排队长度与消散时间的公式,并 通过算例说明根据估算值提前分流,可提高道路的通行能力。 关键词:交通事故;车流波动;排队长度;消散时间;车辆
can
calculation
be improved with
Key words:accident;vehicle flow fluctuating;queue length;dispersing}time; vehicle
卉城市交通中,发生事故后往
lJ一往会引起该路段的车辆排 队,出现交通阻塞,甚至会波及相 邻路段。正确估算车辆排队长度及 消散所需时间,不仅为交通路网中 最短径路的选择提供依据,而且为
取.,一(g—Qy)/(K—K)(1) 式中:暇.,为集散波的波速,km/h;
Q。、Q。为前后两种车流状态的流 量,辆/11;K。、K为前后两种车流状 态的密度,辆/km。 根据交通流模型可知,交通量 Q、行车速度v、车流密度K三者的
关系为:
Q=v×K (2)
用车流波动理论分析车流 排队及消散的过程
密的应相,:Q为变量流求需,化变 :W 为写改式)5(以所。吗为变度 I.Ⅱx
0 =42 8— min 0 ×■×60 6 4 因为7。>Tl,所以假设不成立, 两波相遇时车流需求量已变为Q:。 丁:—(K/-K,l-X,.2)x—To+(K2-K,)xTI 速度缓慢行驶,事故解除后该路段 2=000辆/h, ,S:为变力能行通的 52一:,v:为升上度速驶行的流车 km/h。据资料显示该路段的阻塞密 度Ki=124辆/h,事故发生时段该 1=800 ,Q:为量求需流车的段路 辆/11,车速为:v,=30km/h,可持续 02=,T为间时 2。K一2K
a
间有密切关系。为简单起见,将本 文讨论的交通事故严重程度视为 相同。美国《道路通行能力手册》中 根据车速、流量、密度将公路基本 路段的服务水平分为A、B、c、D、 E、F六个等级,事故发生在不同的 服务等级条件下对车流的影响是 不相同的。在A、B、C服务水平条 件下车流比较稳定,密度较小,若 发生事故,尽管在其附近地区的服
1 =,S:为降下力能行通的段路该
ⅢV/X+丁=4丁
时:S为力能行通段路为Ⅲv:中其
。3算椤9 2K/2S=Ⅲ,1,度速车行的 某路段上发生交通事故,事故
124—100—80 1
点原,置位对相的点故事与示表轴 。表示事故发生点,纵轴的负半轴
表示事故点的上游,正半轴表示事 故点的下游,虚线OA、B表示集 结波,CB表示消散波,其斜率的绝 示表号负正的率斜,速波示表值对 为间时的遇相波两。向方的播传波 丁,当集结波与消散波在丁>0的范 围内有交点时,表示车队可以在有 。散消能不则否,散消内间时限 首先假设两波相遇之前该路 段需求流量始终为O,,OA与cB相 的到达伸延游上向队排示表处交 最远处,设两波相遇时的间为丁, 速波波散消,。.。w为速波波结集 为w。.Ⅲ,则根据两波相遇时波传 :知可系关一这等相离距的动 )5()%一丁(XI11,ⅡW=T×Ⅱ.Iw JWli,mzI茂M卜半)I )半卜小嘏ⅧW姚 则: 瓦×生竺与一丁 散消队车在明说则,,丁>丁若 过 a2=1 通需后之,niar 40辆/h,车速为:1,2=40 km/h。求该事故引起的排队长及 。间时要需所散消队排 解:根据(2)式密度、速度、交通
交通事故在不同服务等级 条件下的影响
交通事故对道路行车造成的
影响,不仅跟事故本身的严重程度 有关,而且与事故发生的地点与时
Abstract:The traditional Queuing Theory’calculates the queue length onl‘y based
on
demand and through capacity.Since it ignores the influence of vehicle
Line&Yard,No.4 Survey&Design Institute of China
Railway,Wuhan,Hubei
2.Tianjin Train&Crew Division,Tianjin Railway Sub—Administration,Tianjin
University,Lanzhou,Gansu
:竺:竺竺墨!?:竺i× 35—80 60—29.8min 则排队长为: x
=卜c卜‘100+80 I×学=6.7km 刮 卜, 半 车队消散时间为: 卜2 x
7 . =39.9 6 min 丁8=丁+瓦2 29・8+丽×60
km/h的
1 5分钟阻塞所 的短短,此因 间时 来消散。交通部门可根据该估计 的钟分04近要需队排的起引 值提前在上游进行分流,从而使排 队车辆减为最少,提高道路的通行 能力。
超1,李新波2,李引珍3
Yin—zhen3
KONG Hui—huil,QIN Cha01,LI Xin—b02,LI
(1.铁道第四勘察设计院线站处,湖北武汉450063;2.天津铁路分局天津车务段, 天津5001 42;5.兰州交通大学,甘肃兰州
(1.Department
of
750070)
430063,China; 300 1
1993年,格林希尔茨(Green— shields)提出了速度一密度线性关 系模型: 1,=vl(1一K/钙)
(3)
式中:v,为畅行速度,即车流密度为 零时,车辆的最大速度;Ki为阻塞 密度,即车流密集到所有车辆无法 移动时的密度。 由以上(1)、(2)、(3)式可以推导 出波速与密度的关系:
暇广v r(1_警当)(4)
as
well
as
the dispersing process after accident and to deduce the
a
calculation formula for queue length and dispersing time.With case,the paper states that the through capacity of road aforehand diffiuence according to calculation.
参考文献:
北 .]M[册手力能行通路道.译,田福任]1[ 京:中国建筑工业出版社,1991.
[2]张邰生.交通工程学基础【M】.北京:人 民交通出版社,2002.
【3]臧华,彭国雄.城市快速道路异常
运 通交 输系统工程与信息,2003,3(2): .】J[究研的间时程行段路下件事 . 收 稿日期: 责任编辑: 95 2004-12—23 —7 尹红 5
交通管理部门正确指挥行车提供 理论根据。传统的排队论理论,单 纯使用需求量和通行能力的关系 推算排队长度,由于未考虑车流波 动的影响,从而使估算结果与实际 出入很大。通过使用车流波动理
务水平会下降,但造成的影响会很 快消除,交通流能迅速恢复原有服 务水平。但在D、E服务水平条件下 交通流处于不稳定阶段,车流密度 较大。交通流量达到或接近路段的 通行能力,任何交通流的干扰和事
2.1车流波动理论 假设上游交通需求量大于事 发路段现有通行能力,到达车流在 事故地点陆续减慢速度甚至停车 而集结成密度较高的队列,事故解 除后,由于路段通行能力的恢复, 排队车辆又陆续加速而疏散成一 列具有适当密度的车队,车流中两 种不同密度部分的分界面经过一 辆辆车向车队后部传播的现象,称 为车流波动。 如图1所示为时间一空间坐标
