高等数学高教五版课件常系数非齐次线性微分方程工科类
合集下载
高数课件第七章微分方程:第八节 常系数非齐次线性微分方程

Pm ( x) e
y*
y1 y1 k x
( i ) x
Pm ( x) e ( i ) x
利用第二步的结果, 根据叠加原理, 原方程有特解 :
Qm (cos x i sin x) ~ x k e x Rm cos x Rm sin x ~ 其中 R m , R m 均为 m 次多项式 .
y
y1 y1
y*
~ 均为 m 次实 所以 y 本质上为实函数 , 因此 Rm , R m
多项式 .
小 结:
对非齐次方程
~ y p y q y e x Pl ( x) cos x P n ( x) sin x
( p, q 为常数 )
Pm ( x) A,
Be x , y* Bxe x Bx 2 e x
不是特征方程的根 是特征方程的单根 , 是特征方程的重根
上述结论可推广到n阶常系数非齐次线性微分方程
y
(n)
p1 y
( n 1)
p n y e Pm ( x)
x
其中: 是常数, Pm ( x) a0 x m a1 x m1 a m 对应齐次方程的特征方程:r n p1 r n 1 p n 0 方程的特解可设为
原方程通解为
y (c1 c 2 x)e
2x
3 2 9 x 3x 4 x 2 e 2 x 2 4
例5 设函数 ( x ) 连续,且满足
( x) e t (t )dt x (t )dt 求 ( x )
x x x 0 0
解
《高等数学教学课件》 第五、六节 常系数线性微分方程共28页

y1
e(i)xe(i)x
2
excosx是
微
分
方;
程
y2
e(i)xe(i)x 2i
exs
inx是
微
分
方;
程
y2 y1
eexxcsionsxxtanx不
恒
等
于 .常 y1, y数 2线
性
无
关 .
微分方 :y c 1 y 程 1 c 2y 2的 e x (c 1c 通 o x s c 解 2six n ).
微分方
程
2 的
通
解 : 为
2
;
yLeabharlann e2x2 (c1
cos
2 2
x
c2
s in
2 2
x)
e
2 x
2 (c3
cos
2 2
x
c4
s in
2 2
x).
解例特 4、求 征方 y方 :4r 42 程 y 程 2 r 35 为 y 5r 20 的 0 r通 .2(r2解 2r5)0
(rr210 )2 4r1 ,20 0 ;或 (rr2 1)2 2r 540 r3,4 12i;
(3)若 . p24q0,
有 一 对 共 轭 r1,2的 i复 . 特 征 根
则 ypyqy 0的 通:y 解 ex 为 (c1cox sc2sin x)
证明 因 r1 ,2 为 i是特 ,所 征 e( 以 i)x 根 ,e( i)x是 微分;方 e ( i)x程 e x e i的 x 欧 拉 e 解 x (公 cx o 式 is six n );
d2x dt2
g 4a
x
0
;
x t0 a, x t0 0
常系数非齐次高阶线性微分方程37页PPT

常系数非齐次高阶线性微分 方程
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
高等数学上册第七章课件.ppt
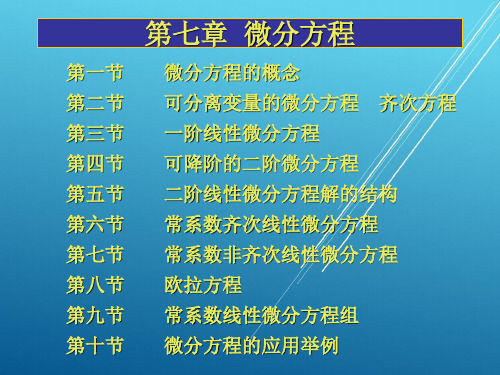
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
高数第十二章常系数非齐次线性微分方程

k x y * xQ ( x ) e m
x 结 论 : 如 果 f ( x ) P ( x ) e ,则 ( 1 ) 的 解 具 有 形 如 : m
的 特 解 , 其 中 Q ( x ) 是 与 P ( x ) 同 次 的 多 项 式 . m m
x Q ( x ) e , 不 是 特 征 根 m x y *x Q )e , 是 单 特 征 根 m(x 2 x x Q ( x ) e , 是 重 特 征 根 m
代 入 上 式 , 比 较 系 数 可 求 出 Q ( x ) , m x 从 而 得 ( 1 ) 的 特 解 为 y * = Q ( x ) x e .
( i i i )如 果 是 特 征 方 程 r p r q0 的 重 根 , 则
2
m
p q0 , , 且 2 p0 , 于 是 有
i x
P P P P i) x i) x l n ( l n ( ( ) e ( ) e 22 i 22 i
P () x e
( i ) x
P () x e
( i ) x
12
P P P P P l n P l n l n 其 中 P ( x ) i ,P ( x ) i 22 i 22 22
其 中 0 , = 2 , P x , P 0 l n
所 给 方 程 对 应 的 齐 次 方 程 为 y y 0 ,
2 特 征 方 程 为 r 1 0 , 特 征 根 r i .
因 i 2 i 不 是 特 征 方 程 的 根 , 所 以 可 设 特 解 为 y * ( a x b ) c o s 2 x ( c x d ) s i n 2 x
x 结 论 : 如 果 f ( x ) P ( x ) e ,则 ( 1 ) 的 解 具 有 形 如 : m
的 特 解 , 其 中 Q ( x ) 是 与 P ( x ) 同 次 的 多 项 式 . m m
x Q ( x ) e , 不 是 特 征 根 m x y *x Q )e , 是 单 特 征 根 m(x 2 x x Q ( x ) e , 是 重 特 征 根 m
代 入 上 式 , 比 较 系 数 可 求 出 Q ( x ) , m x 从 而 得 ( 1 ) 的 特 解 为 y * = Q ( x ) x e .
( i i i )如 果 是 特 征 方 程 r p r q0 的 重 根 , 则
2
m
p q0 , , 且 2 p0 , 于 是 有
i x
P P P P i) x i) x l n ( l n ( ( ) e ( ) e 22 i 22 i
P () x e
( i ) x
P () x e
( i ) x
12
P P P P P l n P l n l n 其 中 P ( x ) i ,P ( x ) i 22 i 22 22
其 中 0 , = 2 , P x , P 0 l n
所 给 方 程 对 应 的 齐 次 方 程 为 y y 0 ,
2 特 征 方 程 为 r 1 0 , 特 征 根 r i .
因 i 2 i 不 是 特 征 方 程 的 根 , 所 以 可 设 特 解 为 y * ( a x b ) c o s 2 x ( c x d ) s i n 2 x
高教社2024高等数学第五版教学课件-6.3 二阶微分方程

表达式有关。下面举例详细说明,请大家注意把握其数学思想方法。
例6 解二阶常系数线性非齐次微分方程
″ − 2 ′ − 3 = (3 + 1) 2
解 (1)求原方程所对应的齐次方程的通解
特征方程为
2 − 2 − 3 = 0
特征根
1 = 3, 2 = −1
所以齐次方程的通解为:
1 3 + 2 −
″ + ′ + = ()
(6.3.7)
的一个特解,则
= 1 1 + 2 2 + ∗
(6.3.8)
是二阶常系数线性非齐次微分方程(6.3.7)通解。其中1 , 2 为任意常数。
定理3中,齐次方程两个线性无关的解已容易求出,剩下的问题是如
何求非齐次方程(6.3.7)的特解 ∗ 。其实,该特解与右边自由项()
2 + 4 + 13 = 0
其解为共轭复根 1,2 = −2 ± 3
所以原方程的通解为 = −2 (1 3 + 2 3 )
(6.3.6)
2、二阶常系数线性非齐次微分方程
定理3 若1 , 2 是齐次方程
″ + ′ + = 0
的两个线性无关的特解, ∗ 是非齐次方程
第六章 常微分方程
第三节 二阶微分方程
一、可降阶的二阶微分方程
【引例1】解微分方程
解
两边积分一次
两边再积分一次
2
2
=
(是常数)
= ′ = = + 1
1
2
= (+ 1 ) = 2 + 1 + 2
例6 解二阶常系数线性非齐次微分方程
″ − 2 ′ − 3 = (3 + 1) 2
解 (1)求原方程所对应的齐次方程的通解
特征方程为
2 − 2 − 3 = 0
特征根
1 = 3, 2 = −1
所以齐次方程的通解为:
1 3 + 2 −
″ + ′ + = ()
(6.3.7)
的一个特解,则
= 1 1 + 2 2 + ∗
(6.3.8)
是二阶常系数线性非齐次微分方程(6.3.7)通解。其中1 , 2 为任意常数。
定理3中,齐次方程两个线性无关的解已容易求出,剩下的问题是如
何求非齐次方程(6.3.7)的特解 ∗ 。其实,该特解与右边自由项()
2 + 4 + 13 = 0
其解为共轭复根 1,2 = −2 ± 3
所以原方程的通解为 = −2 (1 3 + 2 3 )
(6.3.6)
2、二阶常系数线性非齐次微分方程
定理3 若1 , 2 是齐次方程
″ + ′ + = 0
的两个线性无关的特解, ∗ 是非齐次方程
第六章 常微分方程
第三节 二阶微分方程
一、可降阶的二阶微分方程
【引例1】解微分方程
解
两边积分一次
两边再积分一次
2
2
=
(是常数)
= ′ = = + 1
1
2
= (+ 1 ) = 2 + 1 + 2
高等数学:第八讲 二阶常系数线性非齐次微分方程(1)

齐次方程的通解为 Y C1ex C2e3x .
由于这里 0 不是特征根,所以设方程的特解为 y* b1x b0
把它代入方程得
3b1x (2b1 3b0 ) 3x 1
比较系数得
32bb11
3 3b0
1
b1
1, b0
1 3
所以原方程的一个特解为
y* x 1 3
因此所求通解为
y
C1e x
f (x) Pm (x)ex
此时微分方程(1)成为
Pm (x) a0 xm a1xm1
y'' py' qy f (x) Pm (x)ex (3)
am1x am
分三种情形讨论此式:
y'' py' qy f (x) Pm (x)ex (3)
(1)设不是特征方程的 根,即2 p q 0.
C2e3x
(x
1) 3
谢谢
y (C1 C2 x)er x y e x (C 1 cos x C2 sin x)
02 二阶常系数线性非齐次微分方程解法
定理
设 y * (x) 是二阶常系数线性非齐次微分方程(1)的一个特解,
Y C1 y1(x) C2 y2 (x)是方程(1)所对应的齐次方程(2)的通解,
则 y Y y* C1 y1(x) C2 y2 (x) y * (x) 是方程(1)的通解.
二阶常系数 线性非齐次 微分方程(1)
目录
01 二阶常系数线性非齐次微分方程
02 二阶常系数线性非齐次微分方程解法
03
例题
01 二阶常系数线性非齐次微分方程
二阶常系数非齐次线性
齐次微分方程解法
微分方程的一般形式 (一); py' qy f (x) (1)
大学课件高等数学二阶常系数非齐次线性微分方程

(2) 求非齐次方程的特解 x 设 y x 1A e ( 1 是单根 ) A 2 即 y 2 xe x 解得
x
1 特征根 r1 1
所以原方程通解为 y C1e C 2e
2x
2 xe
x
(3) 求原方程的特解 (求函数y的解析表达式)
2 由 y x x 1, 得 y 2 x 1, 且 y ( 0 ) 1,
设y xAe
3 x
将 y , y , y 代入方程,得
A 1 4 ,
y
1 4
xe
3 x
2x
1
C1 e C 2 e
x
2x
2x x( x 1)e
1
2
10
2002年考研数学二, 3分 设 y y ( x ) 是二阶常系数微分方程 py qy e 3 x 满足初始条件 y (0) y (0) 0 y 的特解, 则当 x 0时 , 函数 (A) 不存在. (B) 等于1.
ln( 1 x )
2
二阶常系数非齐次线性微分方程
y( x )
的极限
(D) 等于3.
0 0
(C) 等于2.
2
0 0
解 lim
ln( 1 x )
2
x 0
y( x )
2x lim lim x 0 y( x ) x 0 y ( x ) 2 2 lim x 0 y ( x )
y py qy 0
难点 如何求非齐次方程特解? 方法 待定系数法.
2
二阶常系数非齐次线性微分方程
y py qy Pm ( x )e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢解题步骤
是特征方程的重根 k=2
设特解 写出f(x),明确和m 写出特征方程,确定k
求特解 代入方程,比较系数 列出等式,求出系数
高等数学高教五版课件常系数非齐次线 性微分方程工科类
例1
的一个特解.
解: f ( x ) 3 x 1 , 0 , m 1
对应的齐次方程的特征方程:
不是特征方程的根 . 设所求特解为
f ( x) e x Pl ( x) cos x Pn ( x) sin x
,ω为实数 , Pl ( x) Pn ( x) 分别为l、n次多项式 .
=0 f ( x ) Pl ( x ) cos x Pn ( x) sin x
➢特解形式
y
xke x
R(1) m
(
x
)
cos
x
Rm(2) ( x ) sin
高等数学高教五版课件常系数非齐次线 性微分方程工科类
常系数非齐次线性微分方程
一、 f ( x ) e x Pm ( x ) 型 二、 f ( x ) e x [ Pl ( x ) cos x Pn ( x) sin x]型 三、高阶线性微分方程的物理应用举例
高等数学高教五版课件常系数非齐次线 性微分方程工科类
第七讲 常系数非齐次线性微分方程
高等数学高教五版课件常系数非齐次线 性微分方程工科类
➢思路 二阶常系数线性非齐次微分方程 :
y p y q y f (x) ( p, q 为常数)
通解: y Y y * 解的结构定理
齐次方程通解 非齐次方程特解 ➢关键 求出非齐次方程的特解 ➢方法 待定系数法
3b 4 c 0
a
1 3
,
d
4 9
3c 0
bc0
3d 4a 0
方程的特解
高等数学高教五版课件常系数非齐次线 性微分方程工科类
例5 求方程 y 9 y 18cos 3x 30sin 3x 的通解.
解: 对应的齐次方程的特征方程:r 2 9 0,
特征根
对应齐次方程的通解
f ( x) 18 cos 3 x 30 sin 3 x 0, 3, m 0
根据 f (x) 的特殊形式 , 给出特解 的待定形式, 代入原方程比较两端表达式以确定待定系数 .
高等数学高教五版课件常系数非齐次线 性微分方程工科类
常系数非齐次线性微分方程
一、 f ( x ) e x Pm ( x ) 型 二、 f ( x ) e x [ Pl ( x ) cos x Pn ( x) sin x]型 三、高阶线性微分方程的物理应用举例
例4
的一个特解 .
解: f ( x ) x cos 2 x 0, 2, m 1
对应的齐次方程的特征方程:r 2 1 0
不是特征方程的根, 设特解
代入方程得
(3a x 3b 4 c) cos 2x (3c x 3d 4 a)sin 2x x cos 2x
比较系数 , 得
3a 1
代入方程得: 比较系数, 得
b0
1 ,
b1
1 3
所求特解为
高等数学高教五版课件常系数非齐次线 性微分方程工科类
例2 求方程 y 5 y 6 y x e2 x的通解.
解: 对应的齐次方程的特征方程:r 2 5 r 6 0 ,
特征根
对应齐次方程的通解:
f ( x) xe2 x , 2, m 1 2 是特征方程的单根
为特征方程的单根 , 设非齐次方程特解
代入方程: 6b cos 3x 6a sin 3x
比较系数, 得
因此特解为 y* x ( 5 cos 3x 3sin 3x )
所求通解为
x (5cos 3x 3sin 3x )
高等数学高教五版课件常系数非齐次线 性微分方程工科类
例6 求下列高阶常系数线性非齐次方程的特解形式:
高等数学高教五版课件常系数非齐次线 性微分方程工科类
常系数非齐次线性微分方程
一、 f ( x ) e x Pm ( x ) 型 二、 f ( x ) e x [ Pl ( x ) cos x Pn ( x) sin x]型 三、高阶线性微分方程的物理应用举例
高等数学高教五版课件常系数非齐次线 性微分方程工科类
由初始条件得
C2
2C3
1 2
CC21
1
3 4
C3
1 4
于是所求解为
y 3 ex 1 e2x 1 x
4
4
2
高等数学高教五版课件常系数非齐次线 性微分方程工科类
常系数非齐次线性微分方程
一、 f ( x ) e x Pm ( x ) 型 二、 f ( x ) e x [ Pl ( x ) cos x Pn ( x) sin x]型 三、高阶线性微分方程的物理应用举例
设非齐次方程特解为y* x ( b0 x b1 ) e2 x
代入方程得 2 b0 x b1 2 b0 x
比较系数, 得
b0
1 2
,
b1
1
特解为 y*
x(
1 2
x
1)e2x
.
所求通解为
(
1 2
x2
x )e2x
.
高等数学高教五版课件常系数非齐次线
性微分方程工科类
例3
求解定解问题
y y(0)
3
y 2 y(0)
y
1 y(0)
0
解: 对应的齐次方程的特征方:
特征根
对应齐次方程通解 Y C1 C 2 e x C 3 e2 x
f ( x ) 1, 0, m 0 0 是特征方程的单根
设非齐次方程特解为
代入方程得
故
原方程通解为
y C1 C 2e x C 3e 2 x
高等数学高教五版课件常系数非齐次线 性微分方程工科类
f ( x ) e x Pm ( x ) 为实数 , Pm (x)为 m 次多项式 .
=0 f ( x ) Pm ( x )
多项式函数
m =0 f ( x ) Ae x
指数函数
其它 f ( x ) e x Pm ( x )
指数函数与多项式函数乘积
➢特解形式
不是特征方程的根 k=0
y x kQm ( x )e x 是特征方程的单根 k=1
x
R(1) m
(
x ),
Rm(2) (
x)
为m次多项式
m max{l, n}
+iω 不是特征方程的根 k=0
+iω 是特征方程的根
k=1
➢解题步骤
设特解 写出f(x),明确、ω和m 写出特征方程,确定k
求特解 代入方程,比较系数 列出等式,求出系数
高等数学高教五版课件常系数非齐次线 性微分方程工科类
