最新整理卡方检验习题doc资料
卡方检验习题e

2χ检验练习题一、最正确选择题1.四格表的周边合计不变时,如果实际频数有变化,那么理论频数〔〕。
A.增大B.减小C.不变D.不确定E.随a格子实际频数增减而增减2.有97份血液标本,将每份标本一分为二,分别用血凝试验法和ELISA法对轮状病毒进行诊断,诊断符合情况见下表,欲比拟何种诊断方法的诊断符合率较高,用〔〕统计方法?两种诊断方法的诊断结果血凝试验法ELISA法合计符合不符合符合74 8 82不符合14 1 15合计88 9 97A.连续性校正2χ检验B.非连续性校正2χ检验C.确切概率法D.配对2χ检验〔McNemar检验〕E.拟合优度2χ检验3.做5个样本率的χ2检验,每组样本量均为50,其自由度为〔〕。
A 249B 246C 1D 4E 94.对四格表资料做2χ检验时,如果将四格表的行与列对调,那么对调前后的〔〕。
A.校正2χ值不等B.非校正2χ值不等C.确切概率检验的P值不等D.非校正2χ值相等E.非校正2χ值可能相等,也可能不等二、问答题1.简述2χ检验的根本思想。
2.四格表2χ检验有哪两种类型?各自在运用上有何考前须知?3.什么情况下使用Fisher确切概率检验两个率的差异?4.在回忆性研究和前瞻性研究的四格表中,各自如何定义优势比?三、计算题1.前列腺癌患者121名中,82名接受电切术治疗,术后有合并症者11人;39名接受开放手术治疗,术后有合并症者1人。
试分析两种手术的合并症发生率有无差异?2.苏格兰西南部两个地区献血人员的血型记录见下表,问两地的血型分布是否相同?两地献血人员的血型分布地区血型合计A B O ABEskdale 33 6 56 5 100Annandale 54 14 52 5 125合计87 20 108 10 2253.某医院以400例自愿接受妇科门诊手术的未产妇为观察对象,将其分为4组,每组100例,分别给予不同的镇痛处理,观察的镇痛效果见下表,问4种镇痛方法的效果有无差异?4种镇痛方法的效果比拟镇痛方法例数有效率〔%〕颈麻100 41注药100 94置栓100 89对照100 27练习题答案一、最正确选择题解答1. C2. D3. D4. D二、问答题解答1. 答:在2χ检验的理论公式()22A T Tχ-=∑中,A 为实际频数,T 为理论频数。
卡方检验

2χ检验一、选择题χ检验的是()。
1.下列分析不能用2A 两个独立样本率的比较B.配对设计2×2列联表资料C.多个样本率或构成比的比较D.两个定性变量的关联性分析E.两个独立样本均数的比较2.对2×2列联表,在()情况下需要用Fisher确切概率计算法。
A T<5B T<l或n <40C T<l且n>40D 1≤T<5且n<40E T<5或n<40χ的取值范围是()。
3. 统计量2A.(-∞,∞) B (-∞,0) C (0,∞)D (-1,1)E (-∞,1)4.R ×C 列联表的自由度是( )。
A .R -1B .C -1 C R ×CD .(R -1)×(C -1)E .1-n5.三个样本频率比较,2χ>22,05.0χ,可以认为( )。
A 各总体频率不等或不全相等 B .各总体频率均不相等C .各样本频率均不相等D .各样本频率不等或不全相等E .各总体概率不等或不全相等6.研究大学生吸烟与饮酒的行为,对120名男性大学生调查每人的吸烟与饮酒的情况,结果如下。
要分析吸烟的大学饮酒发生率是否与不吸烟的大学生饮酒发生率相同,用( )饮酒 不饮酒 合计 吸烟 26 24 50 不吸烟 42 28 70 合计6852120A 独立样本2×2列联表2χ检验B 2×2列联表确切概率法C 配对2×2列联表2χ检验D 2×2列联表校正2χ检验E 吸烟与饮酒的关联性分析二、是非判断题1.2χ检验不要求观测变量服从某个特定分布。
()2.2χ检验适用于对定量资料作分析。
()3.对两组病人分别用两种方法治疗,结果如下,经过CR⨯列联表的2χ检验,有05P,说明甲法的疗效优于乙法。
()<.0分组无效好转显效治愈合计甲法64 26 32 186 308乙法20 16 24 32 92合计44 42 96 218 4004.对两个独立样本2×2列联表,当全部的理论数大于5,且两个样本含量之和40n,则对两个样本率的差别作检验时,也可用确切概率法。
卡方检验习题【精选文档】

检验练习题一、最佳选择题1.四格表的周边合计不变时,如果实际频数有变化,则理论频数()。
A.增大B.减小C.不变D.不确定E.随a格子实际频数增减而增减2.有97份血液标本,将每份标本一分为二,分别用血凝试验法和ELISA法对轮状病毒进行诊断,诊断符合情况见下表,欲比较何种诊断方法的诊断符合率较高,用()统计方法?两种诊断方法的诊断结果血凝试验法ELISA法合计符合不符合符合74 8 82不符合14 1 15合计88 9 97 A.连续性校正检验B.非连续性校正检验C.确切概率法D.配对检验(McNemar检验) E.拟合优度检验3.做5个样本率的 2检验,每组样本量均为50,其自由度为()。
A 249B 246C 1D 4E 94.对四格表资料做检验时,如果将四格表的行与列对调,则对调前后的( )。
A.校正值不等B.非校正值不等C.确切概率检验的P值不等D.非校正值相等E.非校正值可能相等,也可能不等二、问答题1.简述检验的基本思想。
2.四格表检验有哪两种类型?各自在运用上有何注意事项?3.什么情况下使用Fisher确切概率检验两个率的差别?4.在回顾性研究和前瞻性研究的四格表中,各自如何定义优势比?三、计算题1.前列腺癌患者121名中,82名接受电切术治疗,术后有合并症者11人;39名接受开放手术治疗,术后有合并症者1人.试分析两种手术的合并症发生率有无差异?2.苏格兰西南部两个地区献血人员的血型记录见下表,问两地的血型分布是否相同?两地献血人员的血型分布地区血型合计A B O ABEskdale 33 6 56 5 100Annandale 54 14 52 5 125合计87 20 108 10 225 3。
某医院以400例自愿接受妇科门诊手术的未产妇为观察对象,将其分为4组,每组100例,分别给予不同的镇痛处理,观察的镇痛效果见下表,问4种镇痛方法的效果有无差异?4种镇痛方法的效果比较镇痛方法例数有效率(%)颈麻100 41注药100 94置栓100 89对照100 27练习题答案一、最佳选择题解答1. C2. D3. D4. D二、问答题解答1.答:在检验的理论公式中,A为实际频数,T为理论频数。
卡方检验 习 题

卡方检验习题一、选择题(一)A1型每一道题下面有A 、B 、C 、D 、E 五个被选答案,请从中选择一个最佳答案。
1、下列不能用2χ检验的是 E 。
A .成组设计的两样本频率的比较B .配对设计的两样本频率的比较C .多个样本频率的比较D .频率分布的比较E .等级资料实验效应间的比较2、通常分析四格表在 B Fisher 精确概率计算法。
A .5T <B .140T n <<或C .140T n <<且D .1540T n ≤<<且E .540T n <<或3、2χ值的取值范围是 C 。
A . 2χ-∞<<∞B .20χ-∞<<C .20χ<<∞D .211χ-<<E .21χ≤4、R C ⨯表的自由度是 D 。
A .1R -B .1C -C .R C ⨯D .()()11R C --E .样本含量减15、三个样本频率比较220.01(2)χχ>,可以认为 A 。
A .各总体频率不等或不全相等B .各总体频率均不相等C .各样本频率均不相等D .各样本频率不等或不全相等E .各总体频率相等(二)A2型每一道题以一个小案例出现,其下面都有A 、B 、C 、D 、E 五个被选答案,请从中选择一个最佳答案。
观察366名疼痛患者针刺不同穴位后的镇痛效果如表7-5所示:表7-5 针刺不同穴位后的镇痛效果穴位镇痛效果合谷 足三里 抚突Ⅰ(基本无效) 38 53 47Ⅱ(效果一般) 44 29 23Ⅲ(较有效) 12 28 19Ⅳ (很有效) 24 16 332243211111366122.0710.01ij ij R R i j i j i j i j A A n P n m n m χ====⎛⎫⎛⎫ ⎪ ⎪=-=-< ⎪ ⎪⎝⎭⎝⎭∑∑∑∑基于以上分析,正确的结论是 C 。
A .各穴位的镇痛效果不全相同B .各穴位的镇痛效果全不相同C .各穴位不同镇痛效果的频率分布不全相同D .各穴位不同镇痛效果的频率分布全不相同E .不能认为各穴位不同镇痛效果的频率分布不全相同(三)A3/A4型:以下提供若干案例,每个案例下设若干题目。
卡方检验

(一) 单项选择题1. 关于样本率p 的分布正确的说法是: A . 服从正态分布 B . 服从2χ分布C . 当n 足够大,且p 和1-p 均不太小,p 的抽样分布逼近正态分布D . 服从t 分布 2. 以下说法正确的是: A . 两样本率比较可用Z 检验 B . 两样本率比较可用t 检验C . 两样本率比较时,有2χ=uD . 两样本率比较时,有22χ=t3. 率的标准误的计算公式是: A .)1(p p - B .np p )1(- C.1-n p D.np p )1(- 4. 以下关于2χ检验的自由度的说法,正确的是: A .拟合优度检验时,2-=n ν(n 为观察频数的个数) B .对一个43⨯表进行检验时,11=ν C .对四格表检验时,ν=4D .若2,05.02,05.0ηνχχ>,则ην>5. 用两种方法检查某疾病患者120名,甲法检出率为60%,乙法检出率为50%,甲、乙法一致的检出率为35%,问两种方法何者为优?A .不能确定B .甲、乙法一样C .甲法优于乙法D .乙法优于甲法 + - 甲法 乙法 合计36.已知男性的钩虫感染率高于女性。
今欲比较甲乙两乡居民的钩虫感染率,适当的方法是:A .分性别比较B .两个率比较的2χ检验C .不具可比性,不能比较D .对性别进行标准化后再做比较 7.以下说法正确的是A .两个样本率的比较可用u 检验也可用2χ检验B .两个样本均数的比较可用u 检验也可用2χ检验C .对于多个率或构成比的比较,u 检验可以替代2χ检验D .对于两个样本率的比较,2χ检验比u 检验可靠 (二) 名词解释1. 实际频数与理论频数 2. 2χ界值表 3. 拟合优度 4. 配对四格表5. 双向有序分类资料 6. 率的标准误7. 多个率的两两比较 8. Fisher 精确概率 9. McNemar 检验 10. Yates 校正 (三) 是非题四个样本率做比较,2)3(05.02χχ> ,可认为各总体率均不相等。
3.2卡方检验(完整修改版)
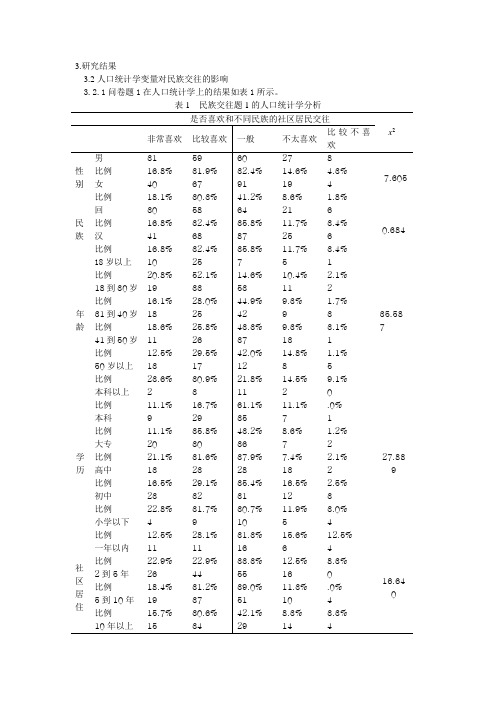
3.研究结果3.2人口统计学变量对民族交往的影响3.2.1问卷题1在人口统计学上的结果如表1所示。
表1 民族交往题1的人口统计学分析由表1分析结果显示:被试在性别上即男女之间没有显著差异,x2=7.605,df =4,p>0.05。
在民族上即回汉之间没有显著差异,x2=0.684,df =4,p>0.05。
在年龄之间存在显著差异,x2=35.587,df =16,p=0.003﹤0.05。
在学历之间没有显著差异,x2=27.889,df =20,p>0.05。
在居住年限之间没有显著差异,x2=16.640,df =12,p>0.05。
3.2.2问卷题2在人口统计学上的结果如表2所示。
表2 民族交往题2的人口统计学分析(注:p﹤0.05)由表2分析结果显示:被试在性别上即男女之间没有显著差异,x2=4.476,df =4,p>0.05。
在年龄之间没有显著差异,x2=23.968,df =16,p>0.05。
在学历之间没有显著差异,x2=17.625,df =20,p>0.05。
在居住年限之间没有显著差异,x2=10.950,df =12,p>0.05。
3.2.3问卷题3在人口统计学上的结果如表3所示。
表3 民族交往题3的人口统计学分析由表3分析结果显示:被试在性别上即男女之间没有显著差异,x2=3.660,df =4,p>0.05。
在年龄之间存在显著差异,x2=24.622,df =16,p>0.05。
在学历之间存在显著差异,x2=41.551,df =20,p=0.03﹤0.05。
在居住年限之间没有显著差异,x2=9.289,df =12,p>0.05。
3.2.4问卷题4在人口统计学上的结果如表4所示。
表4 民族交往题4的人口统计学分析由表4分析结果显示:被试在性别上即男女之间存在显著差异,x2=9.896,df =4,p=0.042﹤0.05。
5习题-卡方检验

计数资料统计分析————习题1.220.05,n x x ≥ 则( )≥0.05 ≤0.05 <0.05 =0.05 >0.052.2x 检验中,自由度v 的计算为( )A.行×列(R ×C )B.样本含量n D.(R -1)(C -1)2.四格表卡方检验中,2x <20.05(1)x ,可认为A.两样本率不同B.两样本率相同C.两总体率不同D.两总体率相同E.样本率与总体率不同3.分析计数资料时,最常用的显著性检验方法是( )检验法 B.正态检验法 C.秩和检验法 D.2x 检验法 E.方差分析4.在卡方界值(2x )表中,当自由度一定时,2x 值愈大,P 值( )A.不变B.愈大C.愈小D.与2x 值相等E.与2x 值无关 5.从甲乙两篇论文中,查到同类的两个率比较的四格表资料以及2x 检验结果,甲论文2x >20.01(1)x ,乙论文2x >20.05(1)x 。
若甲乙两论文的样本量相同,则可认为( )A.两论文结果有矛盾B.两论文结果基本一致C.甲论文结果更可信D.甲论文结果不可信E.甲论文说明两总体的差别大6.计算R ×C 表的专用公式是( )A. 22()()()()()ad bc n x a b a c b d c d -=++++ B. B. 22()b c x b c -=+ C . 221R C A x n n n ⎛⎫=- ⎪⎝⎭∑ D. ()220.5b c x b c --=+E. 22()A T x T -=∑7.关于行×列表2x检验,正确的应用必须是()A.不宜有格子中的实际数小于5 B.不宜有格子中的理论数小于5C.不宜有格子中的理论数小于5 或小于1D.不宜有1/5 以上的格子中的理论数小于5 或有一个格子中的理论数小于l E.不宜有1/5 以上的格子中的实际教小于5 或有一个格子中的实际数小于1×C 表的2x检验中,P<0.05 说明()A.被比较的n 个样本率之间的差异有显著性B.样本率间差别没有显著性C.任何两个率之间差别均有显著性D.至少某两个样本率是差别有显著性E.只有两个样本率间差别有显著性9.四个样本率作比较,220.01,(3)χχ>,可认为()A.各总体率不等或不全相等 B.各总体率均不相等 C.各样本率均不相等D.各样本率不等或不全相等E.各总体率相等10.配对四格表资料需用校正公式的条件()<T<5 和n>40 +c<40 <1 或n<40 >1 n>40 +c<4011.配对资料2x值专用公式是()A.22()()()()()ad bc nxa b a c b d c d-=++++B.2 2()b c xb c-=+C.221R CAx nn n⎛⎫=-⎪⎝⎭∑D.()2 20.5b cxb c--=+E.2 2()A T xT-=∑12.在x2 检验中,四格表的校正公式是:A.22()()()()()ad bc nxa b a c b d c d-=++++B.2 2()b c xb c-=+C.221R CAx nn n⎛⎫=-⎪⎝⎭∑D.()220.5b cxb c--=+E.22()A TxT-=∑13.作四格表卡方检验,当N>40,且__________时,应该使用校正公式A T<5B T>5C T<1D T>5E 1<T<514.四格表资料的卡方检验时无需校正,应满足的条件是( )。
5习题-卡方检验知识讲解

计数资料统计分析————习题1.220.05,n x x ≥ 则( )A.P ≥0.05B.P ≤0.05C.P <0.05D.P =0.05E.P >0.052.2x 检验中,自由度v 的计算为( )A.行×列(R ×C )B.样本含量nC.n-1D.(R -1)(C -1)E.n2.四格表卡方检验中,2x <20.05(1)x ,可认为A.两样本率不同B.两样本率相同C.两总体率不同D.两总体率相同E.样本率与总体率不同3.分析计数资料时,最常用的显著性检验方法是( )A.t 检验法B.正态检验法C.秩和检验法D.2x 检验法 E.方差分析4.在卡方界值(2x )表中,当自由度一定时,2x 值愈大,P 值( )A.不变B.愈大C.愈小D.与2x 值相等E.与2x 值无关 5.从甲乙两篇论文中,查到同类的两个率比较的四格表资料以及2x 检验结果,甲论文2x >20.01(1)x 2x >20.05(1)x 。
若甲乙两论文的样本量相同,则可认为( ) A.两论文结果有矛盾 B.两论文结果基本一致 C.甲论文结果更可信D.甲论文结果不可信E.甲论文说明两总体的差别大6.计算R ×C 表的专用公式是( )A. 22()()()()()ad bc n x a b a c b d c d -=++++ B. B. 22()b c x b c -=+ C . 221R C A x n n n ⎛⎫=- ⎪⎝⎭∑ D. ()220.5b c x b c --=+E. 22()A T x T -=∑7.关于行×列表2x检验,正确的应用必须是()A.不宜有格子中的实际数小于5 B.不宜有格子中的理论数小于5C.不宜有格子中的理论数小于5 或小于1D.不宜有1/5 以上的格子中的理论数小于5 或有一个格子中的理论数小于l E.不宜有1/5 以上的格子中的实际教小于5 或有一个格子中的实际数小于18.R×C 表的2x检验中,P<0.05 说明()A.被比较的n 个样本率之间的差异有显著性B.样本率间差别没有显著性C.任何两个率之间差别均有显著性D.至少某两个样本率是差别有显著性E.只有两个样本率间差别有显著性9.四个样本率作比较,220.01,(3)χχ>,可认为()A.各总体率不等或不全相等 B.各总体率均不相等 C.各样本率均不相等D.各样本率不等或不全相等E.各总体率相等10.配对四格表资料需用校正公式的条件()A.1<T<5 和n>40B.b+c<40C.T<1 或n<40D.T>1 n>40E.a+c<4011.配对资料2x值专用公式是()A.22()()()()()ad bc nxa b a c b d c d-=++++B.2 2()b c xb c-=+C.221R CAx nn n⎛⎫=-⎪⎝⎭∑D.()2 20.5b cxb c--=+E.2 2()A T xT-=∑12.在x2 检验中,四格表的校正公式是:A.22()()()()()ad bc nxa b a c b d c d-=++++B.2 2()b c xb c-=+C . 221R C A x n n n ⎛⎫=- ⎪⎝⎭∑ D. ()220.5b c x b c --=+ E. 22()A T x T -=∑ 13.作四格表卡方检验,当N>40,且__________时,应该使用校正公式A T<5B T>5C T<1D T>5E 1<T<514.四格表资料的卡方检验时无需校正,应满足的条件是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
检验
练习题
一、最佳选择题
1四格表的周边合计不变时,如果实际频数有变化,则理论频数()。
A .增大
B .减小C.不变
D •不确定E.随a格子实际频数增减而增减
2 .有97份血液标本,将每份标本一分为二,分别用血凝试验法和ELISA法对轮状病毒进行诊断,诊断符合情况见下表,欲比较何种诊断方法的诊断符合率较高,用()统计方法?
两种诊断方法的诊断结果
血凝试验法ELISA法合计
血L凝试验也彳厶-符合不符合合计
符合74882
不符合14115
合计88997
A •连续性校正2检验
B •非连续性校正2检验
C .确切概率法
D .配对2
检验(McNemar检验)
2
E .拟合优度检验
3. 做5个样本率的2检验,每组样本量均为50,其自由度为()。
A 249
B 246
C 1
D 4
E 9
2
4•对四格表资料做检验时,如果将四格表的行与列对调,则对调前后的()。
2
A .校正值不等
C .确切概率检验的P值不等B .非校正
D .非校正
2值不等
2
值相等
E. 非校正2值可能相等,也可能不等
、问答题
1简述2检验的基本思想。
2
2. 四格表检验有哪两种类型?各自在运用上有何注意事项?
3. 什么情况下使用Fisher确切概率检验两个率的差别?
4. 在回顾性研究和前瞻性研究的四格表中,各自如何定义优势比?
二、计算题
1•前列腺癌患者121名中,82名接受电切术治疗,术后有合并症者11人;39名接受开放手术治疗,术后有合并症者1人。
试分析两种手术的合并症发生率有无差异?
2.苏格兰西南部两个地区献血人员的血型记录见下表,问两地的血型分布是否相同? 两地献血人
员的血型分布
3•某医院以400例自愿接受妇科门诊手术的未产妇为观察对象,将其分为4组,每组100例,分别给予不同的镇痛处理,观察的镇痛效果见下表,问4种镇痛方法的效果有无差异?
4种镇痛方法的效果比较
镇痛方法例数有效率(%)
颈麻10041
注药10094
置栓10089
对照10027
练习题答案
一、 最佳选择题解答
1. C
2. D
3. D
4. D
二、 问答题解答
2
1. 答:在 检验的理论公式
根据检验假设 H o : n 1 =n 2,若H o 成立,则四个
格子的实际频数 A 与理论频数T 相差不应 很大,即 2统计量不应很大。
若 2值很大,即相对应的 P 值很小,比如 P W a ,则反过来 推断A 与T 相差太大,超出了抽样误差允许的范围,从而怀疑 H o 的正确性,继而拒绝 H o ,
接受其对立假设 H i ,即n 1工冗2。
2.
答:四格表 2检验分为两独立样本率检验和两相关样本率检验。
两独立样本率检。
连续性校正 2检验的理论计算公式为:
abacbdcd
其公式为2
当样本量n 和理论频数T 太小时,如n v 40而且T v 5,或T v 1,或n v 20, 应该用确切概率检验,即 Fisher 检验。
4.
答:暴露组的优势与非暴露组的优势之比就称为优势比,也称为比数比,简记为
OR 。
前瞻性研究暴露组相对于非暴露组关于非暴露组关于“发病”的优势比,即:
AT 2
中,A 为实际频数,T 为理论频数。
T
验应当首先区分其属于非连续性校正 2
检验,或是连续性校正
2
检验。
非连续性校正
2
检验的理论计算公式为: 2
2
A T
,专用计算公式为:
2
ad bc n
A T
E ,专用计算公式为
T
I
.
2
ad bc n 2 n ;两相关样
abacbd c d
本率检验的理论计算公式为:
当样本数据b + c v 40时,需做连续性校正,
3. 答:
;如果资料来自回顾性病例对照研究,则根据“暴露”
bc
相对于“非暴露”的优势计算病例组相对于对照组关于“暴露因素”的优势比,即:
Odd 病例 a b ad Odd 对照
~cd bc
三、计算题解答 1解:
H o :n 1= n 2,两种治疗方法总体合并症发生率无显著差异 H i :n 1工冗2;两种治疗方法总体合并症发生率有明显差异
0.05
2
2
71 1 11 38 121 2
3.483
82 39 12 109 2 12 1 1
查附表8,因为 爲沟 3.84
2
3.483,故P 0.05,按 0.05水准,不拒绝
H o ,即两种治疗方法合并症发生率无显著差异。
2•解:
H 0 :两地的总体血型分布相同 H 1 :两地的总体血型分布不同
0.05
2
225
332 62 562 52
100 87
100 20 100 108
100 10 542 142 522
52
1 5.710
125 87
125 20
125 108 125 10
4 1 2 1
3
查附表8,因为0』5,23
7.81 2
5.710,故 P 0.05, 按
0.05水准,不拒
绝
H 。
,即两地的总体血型分布无显著差异。
3•解:
H 0:n 1= n 2= n 3= n 4,四种镇痛方法总体有效率相同 Odd 暴露 Odd 非暴露
H i:四种镇痛方法总体有效率不同或不全相同
0.05
2400
4
1
2942892272 100251100 251100 251100 251
亠2.2,,2.2
5961173-1
146.17
100 149 100 149 100 149 100 149
4 12 1 3
查附表8,因为 2.005/ 2,3 12.84 2146.175,故P 0.005,按0.05水准,拒绝H0 ,接受H1,即四种镇痛方法总体有效率有显著差异,有效率由高到低依次为注药、
置栓、颈麻和对照。
