习题卡方检验图文稿
第九章 卡方检验12034 ppt课件

结论与之相反。
二、两相关样本率检验 (McNemar检验)
配对四格表资料的 2 检验
与计量资料推断两总体均数是否 有差别有成组设计和配对设计一样, 计数资料推断两个总体率(构成比) 是否有差别也有成组设计和配对设计, 即四格表资料和配对四格表资料。
例 9-3 某 抗 癌 新 药 的 毒 理 研 究 中 , 将
(2 1 )2 ( 1 )1
以 = 1 查 附 表 8 的 2 界 值 表 得 P 0 . 005 。 按 0 . 05
检 验 水 准 拒 绝 H0, 接 受
H
,
1
肺
癌
患
者
癌
胚
抗
原
的
阳性率显著高于健康人,提示可能具有临床诊断价
值。
四格表资料检验的专用公式
2
(adbc)2n
(ab)(ac)(bd)(cd)
表9-3 两种疗法治疗癫痫的效果
治 疗 方 法
治 疗 结 果
有 效
无 效
高 压 氧 组 66( 62.8)
4( 7.2)
常 规 组 38( 41.2)
8( 4.8)
合计 104
12
合 计 有 效 率 ( % )
70 46 116
94.3 82.6 89.7
H 0 :1 2 ,H 1 :1 2 , 0 .0 5
R ×C表 2 检验
行×列表资料
① 多个样本率比较时,有R行2列,称为R ×2表; ② 两个样本的构成比比较时,有2行C列,称
2×C表; ③ 多个样本的构成比比较,以及双向无序分类资
料关联性检验时,有行列,称为R ×C表。
检验统计量
2 n(
卡方检验_精品文档
α=0.05 2.计算χ2值
2 (b c)2 (24 20)2 0.3636
b c 24 20
3.确定P 值,作出统计推论
自由度ν=1 χ2=0.3636<χ20.05(1)=3.84,查
χ2界值表得P>0.05,按α=0.05水
nR nC
17699 17668
572 ... 92 1) 2.56 17693 112 28
3.确定P值
自由度ν=(2 – 1)(4 – 1)=3
χ2 =2.56<χ2 0.05(3)=7.81,则P>
0.05,按α=0.05水准,不拒绝H0, 差异无统计学意义,故不能认为鼻 咽癌患者与眼科病人血型构成1/5以上格子的理论频数小于5, 或有小于1的理论频数。 处理方法: 1)增加样本含量 2)去除上述理论频数过小的行或列 3)合并理论频数太小的性质相近的行 或列
2. 如检验结果拒绝H0,只能 认为各总体率或总体构成比之间 总的来说有差别,但不能说明 它们彼此之间有差别或两两之间 有差别。
α=0.05
2. 计算χ2值
2 n( A2 1) 84( 232 62
nR nC
29 40 29 44
... 32 1) 17.91 11 40
3.确定P值
自由度ν=(3 – 1)(2 – 1) = 2
χ2 =17.91>χ2 0.05(2)=5.99,则
P<0.05,按α=0.05水准,拒绝H0,
117
11.54
合计
20856
604
2.90
3911
127
3.25
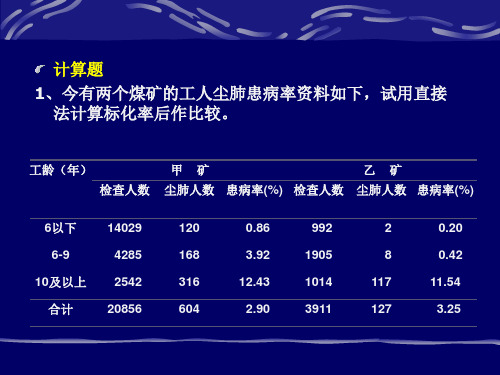
工龄(年) 标准人 口数
甲
试验数据的正态性检验数据的转换及卡方检验图文稿

试验数据的正态性检验数据的转换及卡方检验文件管理序列号:[K8UY-K9IO69-O6M243-OL889-F88688]试验数据的正态检验、数据的转换和卡方检验目录在对试验数据进行方差分析前,应对数据的三性(即同质性、独立性和正态性)进行检验。
本文介绍对资料的正态性进行检验的方法,主要介绍3种检验方法:(1)频数检验——作频率分布图、看偏度系数和峰度系数,(2)作Q-Q图检验,(3)非参数检验——单个样本K-S检验。
下面以两个试验数据为例,例1为84头育肥猪的体重数据,通常符合正态分布。
例2为生长育肥猪7个试验处理组的腹泻率(百分数资料)统计结果,这类资料往往不符合正态,而大多数人以为是符合正态分布,进行方差分析的,因而不能得出正确的结论,却可能得出错误结论。
一、符合正态分布的例子【例1】 84头生长育肥猪的“体重”数据如表1-1,检验该数据是否呈正态分布。
表1-1 84头育肥猪的“体重”数据(排序后)检验方法一:频数检验——作频率分布图、看偏度系数和峰度系数步骤1:数据录入SPSS中,如图1-1。
图1-1 体重数据录入SPSS中步骤2:在SPSS里执行“分析—>描述统计—>频率”,然后弹出“频率”对话框(图1-2a),变量选择“体重”;再点右边的“统计量”按钮,弹出图“频率:统计量”对话框(图1-2b),选择“偏度”和“丰度”(图1-2b);再点右边的“图表”按钮,弹出图“频率:图表”对话框(图1-2c),选择“直方图”,并选中“在直方图显示正态曲线”图1-2a “频率”对话框图1-2b “频率:统计量”对话框图1-2c “频率:图表”对话框设置完后点“确定”后,就会出来一系列结果,包括2个表格和一个图,我们先来看看“统计量”表,如下:统计量体重N有效84缺失0偏度.040偏度的标准误.263峰度-.202峰度的标准误.520偏度系数=0.040,峰度系数-0.202;两个系数都小于1,可认为近似于正态分布。
卡方检验正式文稿演示

组别 甲组 乙组 合计
阳性数 a c
a+c
阴性数 b d
b+d
合计 a+b=n1 c+d=n2
N
率% a/n1 c/n2 (a+c)/N
各组样 本例数 是固定 的
另一个同样重要的分布—χ2卡方分布(Chisquared distribution)。
此分布在1875年,首先由F. Helmet所提出, 而且是由正态分布演变而来的,即标准正态 分布Z值之平方而得
设Xi为来自正态总体的连续性变量。
ui
Xi
u2 i
(Xi )2 2
12
n
u2 i
类似于方差的计算思想,
(x i X ) (A T 0 )2 (A T )2
Pearson χ2检验的基本公式
残差大小是一个相对的概念,
相对于期望频数为10时,20
的残差非常大;可相对于期
望频数为1000时20就很小了。
因此又将残差平方除以期望
频数再求和,以标准化观察
Karl Pearson (1857 – 1936) 频数与期望频数的差别。
检验统计量:χ2 应用:计数资料
基本概念
例1 某院比较异梨醇(试验组)和氢氯塞嗪 (对照组)降低颅内压的疗效,将200名患者 随机分为两组,试验组104例中有效的99例,对 照组96例中有效的78例,问两种药物对降低颅 内压疗效有无差别?
表 200名颅内高压患者治疗情况
编号 年龄 性别 治疗组 舒张压 体温 疗效
行分类
列分类(Y)
合计
(X) 发生数 未发生数
甲
a=a99
b=b5
1a0+4b
卡方检验四格表例题

卡方检验四格表例题卡方检验是用于比较两个或多个样本之间是否存在显著差异的统计方法。
在四格表中,卡方检验可用于比较两个样本的性别、年龄、地区等因素之间的关系是否存在显著差异。
下面是一个例子: 假设我们要比较甲乙两个社区的死亡率是否存在显著差异。
我们随机从甲乙两个社区中各抽取了 100 名居民进行调查,发现甲社区的死亡率为千分之 5.4,乙社区的死亡率为千分之 8.3。
我们需要使用卡方检验来比较这两个社区的死亡率是否存在显著差异。
首先,我们需要画出一个四格表,列出甲乙两个社区的性别、年龄、地区等信息,如下所示:| 甲社区 | 乙社区 || ------ | ------ || 男 | 女 || 5.4 | 8.3 || 男 | 男 || 5.4 | 5.4 || 女 | 女 || 8.3 | 8.3 |接下来,我们可以计算出两个社区的死亡率之间的差异,可以使用卡方检验来进行假设检验。
卡方检验的基本思想是,根据样本数据计算出期望频数和实际频数之间的差异,然后通过卡方值来表达这种差异的程度。
在四格表中,卡方值可以表示为:卡方值 = (列交叉项的期望频数 - 列交叉项的实际频数) / 列交叉项的期望频数例如,在上面的示例中,甲社区的男性和女性的死亡率期望频数为 5.4 和 8.3,而实际频数为 5.4 和 5.4,因此卡方值 = (5.4 - 5.4) / 5.4 = 0。
最后,我们需要根据卡方值和原假设提出一个统计结论。
在本例中,原假设为两个社区的死亡率不存在显著差异,即 H0: μ1 = μ2,其中μ1 和μ2 分别表示甲社区和乙社区的死亡率。
我们要求出 P 值,P 值是指我们在零假设成立的情况下,观察到的卡方值至少大于该值的概率。
在本例中,卡方值为 0,P 值 = 0.999,这意味着我们几乎完全可以拒绝零假设,认为甲乙两个社区的死亡率存在显著差异。
需要注意的是,卡方检验只是一种统计方法,不能保证结论绝对正确。
卡方检验举例PPT课件

Manip>Stack/Unstack>Stack Column…
稳定性及随机性
运行图
Stat>Quality Tool>Run Chart 输出: 4 个 P > 0.05 …证明数据没有“趋势”“成群”“振荡”“混合”
形状
统计描述图
Stat>Basic Statistics>Display Descriptive Statistics...
改进前后均值比较
双样本 T检验(盒形图) Stat>Basic Statistic>2-Sample T-Test
(之前需要F检验)
ANOVA+盒形图
Stat>ANOVA>One-way
输出:如 F检验 P>0.05,需做T检验或ANOVA检验,P<0.05,有改进
6.131
前后独立性测试
卡方检验(Y离散X离散) Stat>Tables>Chi-Square Test… 输出:P < 0.05, 改进有意义
页码 4.49 6.63 4.37 4.109 6.7
6.103 6.94 6.109
6.167
控制
控制阶段主要目的: 证明改善是有效的 使改善保持下去
目的
工具
Minitab
采集改进后数据
数据采集表/采集规则
数据整理
重叠
Manip>Stack/Unstack>Stack Column…
稳定性及随机性
贯彻改进方案质量计划
“书面新流程” “操作公差” “监督评审内容” “对故障的响应计划” 培训操作人员
P12.4
避免错误
第6章 卡方检验 PPT课件

由 χC 2
(|OE|1/2)2可得: E
χ C 2(|8 2 - .7|.7 1 0 5 -.5 )5 6 2 (|8 .7 7|.2 0 5 - 2 .5 )2 5 0 .31 0 .4 90 4 1 .25 06
查附表,
χ2 0.05,1
3.8。4 现
χC 2 1.256002.0,51故应接受
Section 6.2
Fit Test 适合性检验
[例1] 大豆花色一对等位基因的遗传研究,在F2获得表1 所列分离株数。问这一资料的实际观察比例是否符合于3∶1 的理论比值。
表1 大豆花色一对等位基因遗传的适合性测验
花色
F2代实际株数 (O)
理论株数(E)
O-E
紫色
208
216.75 -8.75
0.5
0.4
纵高
0.3 0.2 0.1 0.0
0
自由度=1 自由度=2 自由度=3 自由度=6 a=0.05的临界值
3 3.84 6 7.81 9
1122.59 15
18
卡方值
单侧临界值
➢ 在自由度为
的
2
分布曲线图下,
2 a ,
右方
的面积为
a
,则称
2 a ,
为自由度为
的 2
分布概率为 a 的单侧临界值。可查表。
取 a=0.05。
根据H0的假定,计算各组格观察次数的相应理论次数: 如与146相应的E=(481×160)/547=140.69,
与183相应的E=(481×205)/547=180.26,……, 所得结果填于表4括号内。
根据 2 (OE)2 可得
iE χ 2 ( 1 4 1.6 6 4 )2 9 0 ( 7 8 .7 )2 8 ( 1 1 6 .9 1 )28 5 .62
卡方检验

作业2 卡方测验(一)1.资料:P144习题7.4。
2.数据说明:大麦杂交F2代芒性状表型有钩芒、长芒、短芒三种,测验三种性状是否符合9:3:4比例。
3.结果。
FREQ 过程检验gouxing 频数百分比百分比---------------------------------------钩芒 348 56.13 56.25长芒 115 18.55 18.75短芒 157 25.32 25.00指定比例的卡方检验-------------------------卡方 0.0409自由度 2渐近的 Pr >卡方 0.9798精确的 Pr >= 卡方 0.9797样本大小 = 6204.分析。
H0:三种性状符合9:3:4;H A:不符合。
显著水平:α=0.05 υ=2χ20.05,2=5.99>χ2.因此接受无效假设,无显著差异。
5.程序代码。
optionps=32767ls=255nocenter;data xiti7_4;x 'F:';x 'cd "F:\"';infile 'xiti7_4.csv' dsd;inputgouxing$ zhushu;run;procfreq data=xiti7_4 order=data;weightzhushu;tablesgouxing/nocumtestp=(56.2518.7525);/*ratio of 9:3:4*/exactpchi;run;(二)1.资料:P144习题7.6。
2.数据说明:某杂交组F2得到四种表型,B_C_,B_cc,bbC_,bbcc。
判断四种表型实际观察次数是否符合9:3:3:1的比例,判断是连锁遗传还是独立遗传。
3.结果。
FREQ 过程检验biaoxing 频数百分比百分比----------------------------------------B-C- 132 58.41 56.25B-cc 42 18.58 18.75bbC- 38 16.81 18.75bbcc 14 6.19 6.25指定比例的卡方检验-------------------------卡方 0.6431自由度 3渐近的 Pr >卡方 0.8865精确的 Pr >= 卡方 0.8915样本大小 = 2264.分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题卡方检验
集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)
计数资料统计分析————习题
1.220.05,n x x ≥ 则( )
A.P ≥0.05
B.P ≤0.05
C.P <0.05
D.P =0.05
E.P >0.05
2.2x 检验中,自由度v 的计算为( )
A.行×列(R ×C )
B.样本含量n
C.n-1
D.(R -1)(C -1)
E.n
2.四格表卡方检验中,2x <20.05(1)x ,可认为?
A.两样本率不同
B.两样本率相同
C.两总体率不同
D.两总体率相同
E.样本率与总体率不同
3.分析计数资料时,最常用的显着性检验方法是( )
A.t 检验法
B.正态检验法
C.秩和检验法
D.2x 检验法
E.方差分析
4.在卡方界值(2x )表中,当自由度一定时,2x 值愈大,P 值( )
A.不变
B.愈大
C.愈小
D.与2x 值相等
E.与2x 值无关
5.从甲乙两篇论文中,查到同类的两个率比较的四格表资料以及2x 检验结果,甲论文
2x >20.01(1)x ,乙论文2x >20.05(1)x 。
若甲乙两论文的样本量相同,则可认为( )
A.两论文结果有矛盾
B.两论文结果基本一致
C.甲论文结果更可信
D.甲论文结果不可信
E.甲论文说明两总体的差别大
6.计算R ×C 表的专用公式是( )
A. 22
()()()()()ad bc n x a b a c b d c d -=++++
B. B.
2 2
()
b c x
b c
-
=
+
C.
2
21
R C
A
x n
n n
⎛⎫=-
⎪
⎝⎭
∑
D.
()2 2
0.5
b c
x
b c
--
=
+
E.
2 2
()
A T x
T
-=∑
7.关于行×列表2x检验,正确的应用必须是()
A.不宜有格子中的实际数小于5 B.不宜有格子中的理论数小于5 C.不宜有格子中的理论数小于5 或小于1
D.不宜有1/5 以上的格子中的理论数小于5 或有一个格子中的理论数小于l
E.不宜有1/5 以上的格子中的实际教小于5 或有一个格子中的实际数小于1
8.R×C 表的2x检验中,P<0.05 说明()
A.被比较的n 个样本率之间的差异有显着性
B.样本率间差别没有显着性
C.任何两个率之间差别均有显着性
D.至少某两个样本率是差别有显着性
E.只有两个样本率间差别有显着性
9.四个样本率作比较,
22
0.01,(3)
χχ
>,可认为()
A.各总体率不等或不全相等 B.各总体率均不相等 C.各样本率均不相等
D.各样本率不等或不全相等
E.各总体率相等
10.配对四格表资料需用校正公式的条件()
A.1<T<5 和n>40
B.b+c<40
C.T<1 或n<40
D.T>1 n>40
E.a+c<40
11.配对资料2x值专用公式是()
A.
2
2
()
()()()()
ad bc n
x
a b a c b d c d
-
=
++++
B.
2 2
()
b c x
b c
-
=
+
C.
2
21
R C
A
x n
n n
⎛⎫=-
⎪
⎝⎭
∑
D.
()2 2
0.5
b c
x
b c
--
=
+
E.
2 2
()
A T x
T
-=∑
12.在x2 检验中,四格表的校正公式是:
A.
2
2
()
()()()()
ad bc n
x
a b a c b d c d
-
=
++++
B.
2 2
()
b c x
b c
-
=
+
C.
2
21
R C
A
x n
n n
⎛⎫=-
⎪
⎝⎭
∑
D.
()2 2
0.5
b c
x
b c
--
=
+
E.
2 2
()
A T x
T
-=∑
13.作四格表卡方检验,当N>40,且__________时,应该使用校正公式
A T<5
B T>5
C T<1
D T>5
E 1<T<5
14.四格表资料的卡方检验时无需校正,应满足的条件是( )。
A.总例数大于40
B.理论数大于5
C.实际数均大于l
D.总例数大于40且理论数均大于或等于5
E.总例数小于40
15.某防疫站同时用乳胶凝聚法与常规培养法对110 份乳品作细菌检查,结果如下:
问欲对比两种检验方法的结果有无差别,应采用什么方法()
A.u 检验
B.列联表2x检验
C.配对四格表2x检验
D.配对四格表校正2x检验
E.四格表2x检验
答案
1-5:BDDDCC 6-10:CDDAB 11-15:BAEDD。
