四年级数学包含与排除
奥数四年级--容斥问题(二)

练 1.有30名运动员,其中18人会三级跳,16人 习 会撑杆跳高,10人三级跳远、撑杆跳高均不
会。既会三级跳远又会撑杆跳高的运动员有 多少名?
14名
练 2、操场上的学生排成10路纵队做操,毎路 习 纵队人数同样多,小明站在第四纵队,从排
头数他是第13个,从后往前数他是第8人。 操场上有多少人在做操?
200人
练 3、一个年级有120人爱好数学,100人爱好 习 语文,85人爱好美术,30人既爱好数学又爱
好语文,20人既爱好语文又爱好美术,35人 既爱好美术又爱好数学,有18人三门学科都 爱好。请问:这个年级中数学、语文、美术 三门学科中至少爱好一门学科的学生有多少 人?
238人
练 4、某班全体学生进行了数学、语文、英语 习 三个科目的测试,有8名学生在这三个科目
球、蓝球的学生人数分别为10人,10人,6 人,其中手中既有红球又有黄球的有3人, 既有黄球又有蓝球的有2人,既有蓝球又有 红球的有4人。已知全队每人手中都至少有 一种颜色的球,那么,手中三种颜色的球都 有的多少人?
3人
练 6、某班50名同学全部参加数学、语文、美 习 术三个课外兴趣小组,参加数学小组的有29
17人
18人
15人
求全班人数。
这道题目条件比较复杂,可以根据 题意画出示意图,以便形象直观地 显示他们之间的关系。 全班人数=至少有一个项目达到优 秀的人数+三个项目上都没有达到 优秀的人数
篮球15人 6人 短跑 17人
篮球 游泳 短跑 2人
6人 游泳 18人
6人
经 典 题 型
运用容斥定理 至少有一个项目达到优秀的人数=(短跑达 到优秀人数+游泳达到优秀人数+篮球达到 优秀人数)-(短跑、游泳达到优秀人数+ 游泳、篮球达到优秀人数+篮球、短跑达到 优秀人数)+短跑、游泳、篮球都达到优秀 的人数
包含与排除——精选推荐

和倍问题基本公式和÷(倍数和)=1倍数1倍数⨯倍数=几倍数例1 某校四年级选出48人到区里参加珠算竞赛,其中女同学是男同学的2倍,问:这个学校参加珠算竞赛的男、女生各多少人?练1 五年级学生参加文艺小组和科技小组的共有108人,参加文艺小组的人数是参加科技小组人数的2倍,参加两个小组的各有多少人?练2 师徒二人共加工零件42件,师傅加工数是徒弟的5倍,师徒各加工多少件?例2 小明买了14张画片,小刚买了10张画片,小明送给小刚几张后,小刚的画片张数是小明的3倍?练1 甲、乙两个数之和为72,甲数除乙数商是2,甲、乙两个数各是多少?练2 父子年龄的和是50岁,再过5年父亲的年龄是儿子的4倍,父子现在的年龄各是多少岁?例3 甲、乙二人共有钱810元,甲比乙的3倍还多10元,甲、乙二人各有钱多少元?练1 两个数的和是29,大数除以小数商是4,余数也是4,两个数各是多少?练2 一个除法算式,商是18,余数是4,被除数与除数的和是270,问:除数、被除数各是多少?例4 两个整数相除得商数是12,余数是26,被除数、除数、商数及余数的和等于454。
除数是多少?被除数是多少?练1 被除数比除数的3倍多1,并且被除数、除数、商、余数的和是81,求被除数、除数各是多少?练2 某公社有两个仓库共存粮84吨,已知甲仓库存粮比乙仓库的4倍少1吨,甲、乙两仓库各存粮多少吨?练3 甲站有车192辆,乙站有车48辆,每日从甲站开往乙站的有21辆,从乙站开往甲站的有24辆。
问:如此经过几天后,甲站车辆是乙站车辆的7倍?例5 白、红、黄三种棋子共56颗,白棋子是红棋子的2倍,红棋子是黄棋子的2倍,三种棋子各是多少颗?练1 红、黄、白三种棋子共48颗,红的是黄的3倍,白的是黄的2倍,三种棋子各是多少颗?练2 三个生产队合挖一条长1902米的水渠,第一队挖的是第二队的2倍,第三队挖的是第二队的3倍,三个队各挖了多少米?例6 甲、乙、丙三个数,甲数是乙数的2倍多100,乙数是丙数的2倍多50,已知三个数的和是950,三个数各是多少?练1 胜利化肥厂3天共生产2540袋,第二天生产的比第一天生产的2倍少60袋,第三天生产的比第一天生产的3倍少100袋,三天各生产了多少袋?练2 甲、乙、丙三人,甲的年龄比乙的年龄的2倍还大3岁,乙的年龄比丙的2倍小2岁,三个人年龄之和是109岁,分别求出三个人的年龄。
包含与排除

(二十九)包含与排除(上)《奥赛天天练》第二十一讲《包含与排除》。
包含与排除问题也叫重叠问题,从三年级奥数课堂开始由浅入深逐步学习,此类问题说明及容斥原理具体内容,请查阅:三年级奥数解析(三十九)重叠问题与容斥原理四年级奥数解析(二十九)容斥原理这一讲将在三、四年级学习的基础上,进一步学习运用容斥原理二解答稍复杂的包含与排除问题。
【容斥原理二】如果被计数的事物有A、B、C三类,则:三类元素总个数二A类元素个数+B类元素个数+C类元素个数一既是A类乂是B类的元素个数一既是A类乂是C类的元素个数一既是B类乂是C类的元素个数+既是A类乂是B类又是C类的元素个数。
【原理证明】如下图,三个圆片两两重叠,用红色圆片面积表示A类事物元素个数、黄色圆片面积表示B类事物元素个数、蓝色圆片面积表示C类事物元素个数,三个圆片覆盖的总面积就表示三类元素的总个数:A、B、C三个圆片共同重叠的正中间的一块,覆盖了三层圆片,重叠了2次;剩下的重叠部分都覆盖了两层圆片,重叠了1次。
三个圆片覆盖的总面积就等于三个圆片的面积之和减去重叠部分的面积,重叠1次的减去重叠面积,重叠2次的减去重叠面积的2倍。
但用三个圆片的总面积依次减去AB的重叠部分、AC的重叠部分和BC的重叠部分,重叠1次的面积正好减去了,可三个圆片共同重叠的部分既属于AB的重叠部分,也属于AC的重叠部分,同时属于BC的重叠部分。
这一块儿面积重叠2次,却减去了3次,多减了1次,要补上去。
所以:三类元素总个数二A类元素个数+B类元素个数+C类元素个数一既是A类乂是B类的元素个数一既是A类乂是C类的元素个数一既是B类乂是C类的元素个数+既是A类乂是B类又是C类的元素个数。
【题目】:在参加数学竞赛的46人中,做对第二题的有32人,做对笫4题的有24人,两道题都做对的有20人,两道题都没有做对的有儿人?【解析】:用做对第2题与做对第4题的人数和,减去两题都做对的人数(重叠部分),求出的就是这两题中至少做对了一题的人数:32+24-20=36 (人)。
四年级三大原理包含与排除学生版

包含与排除知识要点在一些计数问题中,经常遇到有关集合元素个数的计算。
求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B=+-U I (其中符号“U”读作“并”,相当于中文“和”或者“或”的意思;符号“I”读作“交”,相当于中文“且"的意思。
),则称这一公式为包含与排除原理,简称容斥原理。
图示如下:I,即阴影面积。
A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A B1、先包含——A B+重叠部分A BI计算了2次,多加了1次;2、再排除——A B A B+-I把多加了1次的重叠部分A BI减去。
两者容斥【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条。
已知焊接部分长4厘米,焊接后这根铁条有多长?包含与排除原理告诉我们,要计算两个集合A B 、的并集A B U 的元素的个数,可分以下两步进行: 第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =I (意思是“排除”了重复计算的元素个数)。
A 类、B 类与C 类元素个数的总和=A 类元素的个数+B 类元素个数+C 类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数。
用符号表示为:A B C A B C A B B C A C A B C =++---+U U I I I I I图示如下:图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数。
1. 先包含——A B C ++A B I 、B C I 、C A I 重叠了2次,多加了1次。
2. 再排除——A B C A B B C A C ++---I I I重叠部分A B C I I 重叠了3次,但是在进行A B C A B B C A C ++---I I I 计算时都被减掉了。
包含与排除(容斥原理)

包含与排除(容斥原理)学生姓名:年级:小升初科目:数学授课教师:贺琴授课时间:学生签字:包含与排除(容斥原理)集合是指具有某种属性的事物的全体,它是数学中的最基本的概念之一。
如某班全体学生可以看作是一个集合,0、1、2、3、4、5、6、7、8、9便组成一个数字集合。
组成集合的每个事物称为这个集合的元素。
如某班全体学生组成一个集合,每一个学生都是这个集合的元素,数字集合中有10个元素。
两个集合中可以做加法运算,把两个集合A、B合并在一起,就组成了一个新的集合C。
计算集合C的元素的个数的思考方法主要是包含与排除:先把A、B的一切元素都“包含”进来加在一起,再“排除”A、B两集合的公共元素的个数,减去加了两次的元素,即:C=A+B-AB。
在解包含与排除问题时,要善于使用形象的图示帮助理解题意,搞清数量关系的逻辑关系。
有些语言不易表达清楚的关系,用了适当的图形就显得很直观、很清楚,因而容易进行计算。
1、六年级96名学生都订了报纸,有64人订了少年报,有48人订了小学生报。
两种报纸都订的有多少人?[分析]用左边的圆表示订少年报的64人,右边的圆表示订小学报的48人,中间重叠部分表示两种报刊都订的人数。
显然,两种报刊都订的人数被统计了两次:64+48=112人,比总人数多112-96=16人,这16人就是两种报刊都订的人数。
【练习】1、一个班的52人都在做语文和数学作业。
有32人做完了语文作业,有35人做完了数学作业。
语文、数学作业都做完的有多少人?2、六年级有122人参加语文、数学考试,每人至少有一门功课得优。
其中语文得优的有65人,数学得优的有87人。
语文、数学都得优的有多少人?3、某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。
如果两次测验都没得过满分的学生有17人,那么,两次测验都得满分的有多少人?2、某校教师至少懂得英语和日语中的一种语言。
已知有35人懂英语,34人懂日语,两种语言都懂的有21人。
【思维拓展】数学四年级思维拓展之包含与排除(附答案)

四年级思维拓展之包含与排除1.把长38厘米和53厘米的两根铁条焊接成一根铁条。
已知焊接部分长4厘米,焊接后这根铁条有多长?2.某小学三年级四班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。
这个班有多少人参加了语文或数学兴趣小组?3.在前100个自然数中,能被2或3整除的数有多少个?4.某科室有12人,其中6人会英语,5人会俄语,5人会日语,有3人既会英语又会俄语,有2人既会俄语又会日语,有2人既会英语又会日语,有1人英、日、俄这三种语言全会,只会一种外语的人比一种外语也不会的人多多少人?5.全班有46名同学,仅会打乒乓球的有18人,既会打乒乓球又会打羽毛球的有7人,既不会打乒乓球又不会打羽毛球的有6人。
问:仅会打羽毛球的有多少人?6.某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。
这个班既没参加美术小组也没参加音乐小组的有多少人?7.有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语。
问既懂英语又懂俄语的有多少人?8.三年级科技活动组共有63人。
在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中,老师到时清点发现:剪贴好一辆汽车模型的同学有42人,装配好一架飞机模型的同学有34人。
每个同学都至少完成了一项活动。
问:同时完成这两项活动的同学有多少人?9.在春光小学“创造杯”展览会上,展品中有26件不是六年级的,有25件不是五年级的.已知五、六年级展品共35件,那么五年级的展品有____件.10.四1班有48名学生,在一节自习课上,写完语文作业的有30人,写完数学作业的有20人,语文数学都没写完的有6人。
(1)问语文数学都写完的有多少人?(2)只写完语文作业的有多少人?参考答案1.【解答】分析:焊接部分为两根铁条的重合部分,由包含排除法知,焊接后这根铁条长:38+53-4=87(厘米)。
2.【解答】分析:如图所示,A圆表示参加语文兴趣小组的人,B圆表示参加数学兴趣小组的人,A与B重合的部分C(阴影部分)表示同时参加两个小组的人。
包含与排除

复习盈亏问题1、少先队员到山上植树,如果每人载4棵,还剩18棵树苗,如果每人栽8棵,则少6棵树苗。
问:有多少名少先队员?多少棵树苗?2、活动课某班同学们参加拔河比赛,分成若干组,每组8人。
后来改成12人,结果少两组。
问全班有多少人?3、老师给大班小朋友分桃子,若8位小朋友每人分到3个,其余小朋友各分到5个,则还余54,若每人分到7个则正好分完。
问小朋友人数和桃子总数?4同学们秋游去公园划船,如果租船增加1条,那么正好每条船坐6人,如果少一条那么正好每条船坐8人。
问这个班共有多少人?包含与排除1、同学们到图书馆借书。
四(1)同学每人都借到课外书,其中借文艺书有40人,借科技书的有30人,两种书都借的有25,四(1)班共有多少人?2、四年级二班有46人,其中会弹琴的有30人,会拉小提琴的有28人,则这个班既会弹钢琴又会拉小提琴的有多少人?3、期末考试小芳的语文成绩和自然成绩加起来是187分,语文成绩和数学成绩加起来195分,数学成绩和自然成绩加起来是190分,那么小芳的语文成绩是多少?4、小玲会唱19首歌,小丽会唱24首歌,两人一共会唱的歌有36首,两人会唱的歌有几首?5、一个班级有48人,班主任在会上问:“谁做完语文作业的?这时有37人举手,又问”谁做完数学作业的有42人举手。
最后问“谁语文、数学作业都没有做完的?没有人举手。
这个班级语文、数学作业都玩的有多少?6、某班级40人在一次体育达标测试中,立定跳远达标的有26人,50米跑达标的有24人,两项都达标的有15人,有多少人两项都没有达标?7、四年级有48人,23人参加科技小组,26人参加文艺小组,12人两个小组都参加了。
有多少人两个小组都没有参加?8、一个旅行团有40人,其中会英语的有24人,会俄语的有18人,两样都不会的有14人,那么,两样都会的有多少人?9、某校进行体育竞赛,项目有短跑、游泳、跳高。
其中参加短跑的有75人,游泳的有52人,跳高的有38人,同时参加短跑与游泳的有26人、短跑与跳高有22人、游泳与跳高的有10人;三项都参加的有2人。
奥数四年级--容斥问题(一)
经 例2、有62名学生,其中会弹钢琴的有11人,会吹竖笛的有56人,
典 两样都不会的有4人,两样都会的有多少人?
题 依题意,画圈框图。
总人数62人
型 依图可知,会弹钢琴+会竖笛
=11+56=67人, 67 > 总人数62人
会弹钢琴的 会两样 会吹竖笛
有11人
?人
既不是5的倍数,也不是7的倍数??。
(3)求既是5的倍数又是7的倍数的数量: 1000÷35 = 28...20
总1--1000的自然数
(4)根据容斥原理: 是5或7的倍数的数有: 200+142-28=314
(5)既不是5,也不是7的倍数的: 1000-314=686
5的倍数 有200
5和7的 公倍数
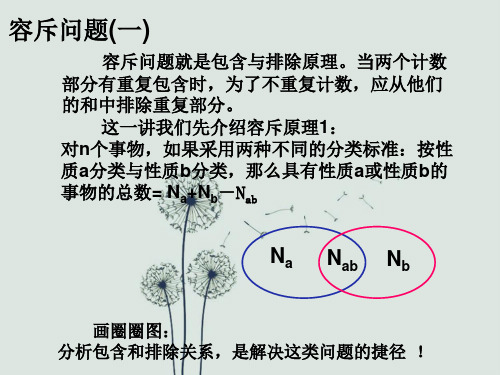
容斥问题(一)
容斥问题就是包含与排除原理。当两个计数 部分有重复包含时,为了不重复计数,应从他们 的和中排除重复部分。
这一讲我们先介绍容斥原理1: 对n个事物,如果采用两种不同的分类标准:按性 质a分类与性质b分类,那么具有性质a或性质b的 事物的总数= Na+Nb-Nab
Na Nab Nb
画圈圈图: 分析包含和排除关系,是解决这类问题的捷径 !
48名
练 9、有一根36cm长的绳子,从一端开始每隔3 习 厘米做一个记号,每隔4厘米也做一个记号,
然后把标有记号的地方剪断。绳子共被剪成 了多少段?
18段
练 10、科技节那天,学校的科技室里展出了每 习 个年级学生的科技作品,其中有114件不是
一年级的,有96件不是二年级的,一、二年 级参展的作品共32件。其他年级参展的作品 共有多少件?
分析搞清数量关系,是解决数学问题的不二法门。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.某班学生去图书室借书,每人都借了课外书,统计结果是:借语文书的有39人,借数学书的32人,语文、数学两种书都借的有26人。
全班学生共几人?
2.桥南小学三年级学生采集标本,采集昆虫标本的有27人,采集植物标本的有21人,两种标本都采集的有8人。
全班共有学生多少人?
3.一个班有学生54人,参加数学课外活动的有38人,参加语文课外活动的有29人。
至少有多少人两样活动都参加了?
4.某班36个同学在一次测验中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问:有几个同学两题都不对,
5.一个班42名学生都订了报纸,订阅《中国少年报》的有32人,订阅《小学生报》的有27人。
有多少人订阅两种报纸?
6.有40名运动员,其中有25人会摔跤,有20人会击剑,有10人击剑、摔跤都不会。
问:既会摔跤又会击剑的运动员有多少人?
7.某校开运动会,参加比赛项目的人数如下:参加田赛的有26人,参加径赛的有30人,其中既参加田赛又参加径赛的有12人,田赛和径赛都没参加的有4人。
这个班共有学生多少人?
8.在50名出国人员中,有4人既不懂英语,也不懂日语,但其中有37人懂英语,有43人懂日语。
有多少人既懂英语又懂日语?
9.明明幼儿园大班里,会弹钢琴的有25人,会拉手风琴的有20人,既会弹钢琴又会拉手风琴的有15人,这两样都不会的有10人,这个班一共有多少人?
10.全班有50名同学,只参加数学小组的有27人,既参加教学小组又参加作文小组的有5人,两个小组都没参加的有4人,求只参加作文小组的有几人?
11.有50名同学参加了短跑和跳远的达标测试,短跑达标的有38名,跳远达标的有31名,两项都达标的有22名。
这两项都没达标的有几名?
12.学校田径队有40人上场参加比赛。
有18人参加田赛,有28人参加径赛,请问只参加田赛与只参加径赛的人数共是多少?
13.某班成立英语和微机小组,有25人参加英语小组,其中10人既参加了英语小组又参加了微机小组,没有参加微机小组的有18人。
请问有多少人两个小组都没参加?
14.某班52名同学,在一次测验中.答错第一题的有29人,答错第二题的有14人,这两道题都答对的有16人。
问有几个同学这两道题都没答对?
15.某班开展课外活动,每名学生至少参加一个小组。
参加文艺小组的有38人,参加体育小组的有32人,既参加文艺小组又参加体育小组的有12人,这个班一共有学生多少人?
16.某校先后举行了数学、语文、自然三科竞赛,参加竞赛时学生中,至少参加一科的有:数学498人,语文525人,自然499人;至少参加两科的有:数学、语文330人、数学、自然297人,语文、自然328人;三科都参加的有234人。
求参加竞赛的学生总数。
17.26名男同学中喜欢打篮球的13人,喜欢打排球的12人,喜欢踢足球的9人,既喜欢篮球又喜欢足球的有2人,既喜欢足球又喜欢排球的有3人,但没有一个男同学同时喜欢三种球类,也没有不喜欢任何一种球的。
有多少男同学既喜欢篮球,又喜欢排球?
18. 五一班30人有14人参加径赛,9人参加田赛,两项都没有参加的有12人,既参加径赛又参加田赛的有多少人?。
