排列组合1
四年级奥数-排列组合(1)

排列组合排列组合问题是必考题,它联系实际生动有趣,但题型多样,思路灵活,不易掌握,实践证明,掌握题型和解题方法,识别模式,熟练运用,是解决排列组合应用题的有效途径;下面就谈一谈排列组合应用题的解题策略.1.相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列.例 1.,,,,A B C D E 五人并排站成一排,如果,A B 必须相邻且B 在A 的右边,那么不同的排法种数有A 、60种B 、48种C 、36种D 、24种解析:把,A B 视为一人,且B 固定在A 的右边,则本题相当于4人的全排列,4424A =种,答案:D .2.相离问题插空排:元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端.例2.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是A 、1440种B 、3600种C 、4820种D 、4800种解析:除甲乙外,其余5个排列数为55A 种,再用甲乙去插6个空位有26A 种,不同的排法种数是52563600A A =种,选B .3.定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序,可用缩小倍数的方法.例 3.,,,,A B C D E 五人并排站成一排,如果B 必须站在A 的右边(,A B 可以不相邻)那么不同的排法种数是A 、24种B 、60种C 、90种D 、120种解析:B 在A 的右边与B 在A 的左边排法数相同,所以题设的排法只是5个元素全排列数的一半,即551602A =种,选B . 4.标号排位问题分步法:把元素排到指定位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成.例4.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有A 、6种B 、9种C 、11种D 、23种解析:先把1填入方格中,符合条件的有3种方法,第二步把被填入方格的对应数字填入其它三个方格,又有三种方法;第三步填余下的两个数字,只有一种填法,共有3×3×1=9种填法,选B .5.有序分配问题逐分法:有序分配问题指把元素分成若干组,可用逐步下量分组法. 例5.(1)有甲乙丙三项任务,甲需2人承担,乙丙各需一人承担,从10人中选出4人承担这三项任务,不同的选法种数是A 、1260种B 、2025种C 、2520种D 、5040种解析:先从10人中选出2人承担甲项任务,再从剩下的8人中选1人承担乙项任务,第三步从另外的7人中选1人承担丙项任务,不同的选法共有2112520C C C =种,选C .(2)12名同学分别到三个不同的路口进行流量的调查,若每个路口4人,则不同的分配方案有A 、4441284C C C 种B 、44412843C C C 种 C 、4431283C C A 种D 、444128433C C C A 种 答案:A .6.全员分配问题分组法:例6.(1)4名优秀学生全部保送到3所学校去,每所学校至少去一名,则不同的保送方案有多少种?解析:把四名学生分成3组有24C 种方法,再把三组学生分配到三所学校有33A 种,故共有234336C A =种方法.说明:分配的元素多于对象且每一对象都有元素分配时常用先分组再分配.(2)5本不同的书,全部分给4个学生,每个学生至少一本,不同的分法种数为A 、480种B 、240种C 、120种D 、96种答案:B .7.名额分配问题隔板法:例7.10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案?解析:10个名额分到7个班级,就是把10个名额看成10个相同的小球分成7堆,每堆至少一个,可以在10个小球的9个空位中插入6块木板,每一种插法对应着一种分配方案,故共有不同的分配方案为6984C =种.8.限制条件的分配问题分类法:例8.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?解析:因为甲乙有限制条件,所以按照是否含有甲乙来分类,有以下四种情况: ①若甲乙都不参加,则有派遣方案48A 种;②若甲参加而乙不参加,先安排甲有3种方法,然后安排其余学生有38A 方法,所以共有383A ;③若乙参加而甲不参加同理也有383A 种;④若甲乙都参加,则先安排甲乙,有7种方法,然后再安排其余8人到另外两个城市有28A 种,共有287A 方法.所以共有不同的派遣方法总数为433288883374088A A A A +++=种.9.多元问题分类法:元素多,取出的情况也多种,可按结果要求分成不相容的几类情况分别计数,最后总计.例9.(1)由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有A 、210种B 、300种C 、464种D 、600种解析:按题意,个位数字只可能是0、1、2、3和4共5种情况,分别有55A 、113433A A A 、113A A A 、113233A A A 和1333A A 个,合并总计300个,选B .(2)从1,2,3…,100这100个数中,任取两个数,使它们的乘积能被7整除,这两个数的取法(不计顺序)共有多少种?解析:被取的两个数中至少有一个能被7整除时,他们的乘积就能被7整除,将这100个数组成的集合视为全集I,能被7整除的数的集合记做{}7,14,21,98A =共有14个元素,不能被7整除的数组成的集合记做{}1,2,3,4,,100I A =共有86个元素;由此可知,从A 中任取2个元素的取法有214C ,从A 中任取一个,又从I A 中任取一个共有111486C C ,两种情形共符合要求的取法有2111414861295C C C +=种. (3)从1,2,3,…,100这100个数中任取两个数,使其和能被4整除的取法(不计顺序)有多少种?解析:将{}1,2,3,100I =分成四个不相交的子集,能被4整除的数集{}4,8,12,100A =;能被4除余1的数集{}1,5,9,97B =,能被4除余2的数集{}2,6,,98C =,能被4除余3的数集{}3,7,11,99D =,易见这四个集合中每一个有25个元素;从A 中任取两个数符合要;从,B D 中各取一个数也符合要求;从C 中任取两个数也符合要求;此外其它取法都不符合要求;所以符合要求的取法共有211225252525C C C C ++种. 10.交叉问题集合法:某些排列组合问题几部分之间有交集,可用集合中求元素个数公式()()()()n A B n A n B n A B =+-.例10.从6名运动员中选出4人参加4×100米接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同的参赛方案?解析:设全集={6人中任取4人参赛的排列},A={甲跑第一棒的排列},B={乙跑第四棒的排列},根据求集合元素个数的公式得参赛方法共有:()()()()n I n A n B n A B --+⋂43326554252A A A A =--+=种.11.定位问题优先法:某个或几个元素要排在指定位置,可先排这个或几个元素;再排其它的元素。
排列组合的常见模型(1)

4 n 4 3 34 排列组合的常见模型(一)处理排列组合问题的常用思路:1、特殊优先:对于题目中有特殊要求的元素,在考虑步骤时优先安排,然后再去处理无要求 的元素。
例如:用0,1, 2,3, 4 组成无重复数字的五位数,共有多少种排法?解:五位数意味着首位不能是 0,所以先处理首位,共有 4 种选择,而其余数位没有要求,只需将剩下的元素全排列即可,所以排法总数为 N = 4 ⨯ A 4= 96种 2、寻找对立事件:如果一件事从正面入手,考虑的情况较多,则可以考虑该事的对立面,再 用全部可能的总数减去对立面的个数即可。
例如:在 10 件产品中,有 7 件合格品,3 件次品。
从这 10 件产品中任意抽出 3 件,至少有一件次品的情况有多少种解:如果从正面考虑,则“至少 1 件次品”包含 1 件,2 件,3 件次品的情况,需要进行分类讨论,但如果从对立面想,则只需用所有抽取情况减去全是正品的情况即可,列式较为简单。
N = C 3 - C 3 = 85 (种)1073、先取再排(先分组再排列):排列数 A m是指从 n 个元素中取出 m 个元素,再将这 m 个元素进行排列。
但有时会出现所需排列的元素并非前一步选出的元素,所以此时就要将过程拆分成两个阶段,可先将所需元素取出,然后再进行排列。
例如:从 4 名男生和 3 名女生中选 3 人,分别从事 3 项不同的工作,若这 3 人中只有一名女生,则选派方案有多少种。
解:本题由于需要先确定人数的选取,再能进行分配(排列),所以将方案分为两步,第一步:确定选哪些学生, 共有 C 2C 1 种可能, 然后将选出的三个人进行排列: A 34 33C 2C 1 A 3 = 108 种方案(二)排列组合的常见模型1、捆绑法(整体法):当题目中有“相邻元素”时,则可将相邻元素视为一个整体,与其他元素进行排列,然后再考虑相邻元素之间的顺序即可。
例如:5 个人排队,其中甲乙相邻,共有多少种不同的排法解:考虑第一步将甲乙视为一个整体,与其余 3 个元素排列,则共有 A 4种位置,第二步考虑。
3、组合数学第三章排列组合(1)
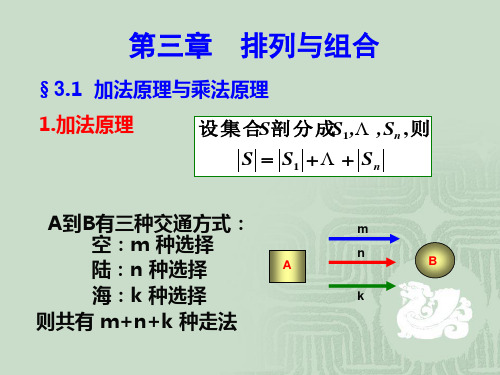
P(5,3)
(2)同(1),若不限制每天考试的次数,问有多 少种排法?
53
例3.8 排列26个字母,使得在a 和 b之间正好有7个 字母,问有多少种排法?
例3 用26个字母排列,是元音 a,e,i,o,u 组不相继 出现,有多少种排法?
(1)排列所有辅音:P(21,21)=21! (2)在辅音前后的22个空档中排元音:
n2 +... + nk .
2若r=n,则N= n! ; n1 !n2 !...nk !
3若r < n且对一切i,i =1, 2,..., k,有ni ? r,则N=kr ; 4若r < n,且存在着某个ni < r,则对N没有一般的求解公式。
§3.5 多重集的组合
多重集S中r个元素进行无序选择,构成一个多重 集的r-组合。 篮子里有2个苹果,1个桔子,3个香蕉,篮子里 的水果构成“多重集”。
解1 (1)任意坐: n=9! (2)不相邻:A先就坐,B不相邻:7 其余8人排序:8! m=7*8! (3) P=m/n=7*8!/9!=7/9
例6 10个人为圆桌任意就坐,求指定的两个人 A与B不相邻的概率。
解2 (1)任意坐: n=9! (2)A,B相邻:A先就坐,B左右相邻:2 其余8人排序:8! k=2*8! (3)不相邻:m=9!-2*8! (4) 两人不相邻的概率 P=m/n=(9!-2*8!)/9!=1-2/9=7/9
证明
(1) 从{ 1,2,…,n }中选出2-组合有
C
2 n
(2) 另一种选法:
最大数为k的2-组合共有k-1个,k=1,2,…,n
有加法原理,共有 0+1+2+…+(n-1) 个2-组合
排 列 组 合 公 式 及 排 列 组 合 算 法

排列组合1. 排列组合公式quad排列与组合二者的区别,排列计较次序而组合不计序。
quad从n从n从n个不同物件随机取rrr个物件,记排列数和组合数分别为AnrA_n^rAnr?和CnrC_n^rCnr?,则:Anr=n(n?1)?(n?r?1)=n!(n?r)!Cnr=Anrr!=n!r!(n?r)!begin{aligned}amp; A_n^r=n(n-1)cdots(n-r-1)=frac{n!}{(n-r)!}amp; C_n^r=frac{A_n^r}{r!}=frac{n!}{r!(n-r)!}end{aligned}Anr=n(n1)(nr1)=(nr)!n!Cnr=r!Anr=r!(nr)!n!quad注:Anr(n≥r≥1)A_n^r(ngeq r geq 1)Anr?(n≥r≥1),Cnr(n≥r≥0)C_n^r(ngeq r geq 0)Cnr?(n≥r≥0),0!=10!=10!=1,Cn0=1C_n^0=1Cn0?=12. 二项式及公式推广quad二项式展开公式为:(a+b)n=∑i=0nCniaibn?i(a+b)^n=sum_{i=0}^nC_n^ia^ib^{n-i}(a+b)n=i=0∑n?Cni?aibn?iquad系数CnrC_n^rCnr?常称为二项式系数。
由(a+b)n=(a+b)?(a+b)?n(a+b)^n=underbrace{(a+b)cdots(a+b)}_{n} (a+b)n=n(a+b)?(a+b)?,若独立nnn次实验从{a,b}{a,b}{a,b}中取数,则有CniC_n^iCni?种情况取到iii个aaa、n?in-in?i个bbb,故aibn?ia^ib^{n-i}aibn?i项的系数为CniC_n^iCni?。
quad(1) ∑i=0nCni=2nsum_{i=0}^n C_n^i=2^n∑i=0n?Cni?=2n quadquad 当a=b=1a=b=1a=b=1时,(a+b)n=2n=∑i=0nCni(a+b)^n=2^n=sum_{i=0}^nC_n^i(a+b)n=2n=∑i=0n?Cni?;quad(2)Cm+nk=∑i=0kCmiCnk?iC_{m+n}^k=sum_{i=0}^kC_m^iC_n^{k-i}Cm+n k?=∑i=0k?Cmi?Cnk?i?quadquad 因为(1+x)m+n=(1+x)m(1+x)n(1+x)^{m+n}=(1+x)^m(1+x)^n(1+x)m+n=(1+ x)m(1+x)n,即∑j=0m+nCm+njxj=(∑j=0mCmjxj)?(∑j=0nCnjxj)sum_{j=0}^{m+n}C _{m+n}^jx_j=(sum_{j=0}^mC_m^jx_j)cdot(sum_{j=0}^nC_n^jx_j)∑j=0m+n?Cm+nj?xj?=(∑j=0m?Cmj?xj?)?(∑j=0n?Cnj?xj?),由等式两边同幂项系数相同知Cm+nk=∑i=0kCmiCnk?iC_{m+n}^k=sum_{i=0}^kC_m^iC_n^{k-i}Cm+n k?=∑i=0k?Cmi?Cnk?i?。
组合数学排列组合(1)格路模型,范德蒙德恒等式

组合数学排列组合(1)格路模型,范德蒙德恒等式
1.排列(permutation):
从n个不同的元素中,取出r个不重复的元素,按次序排列,称为从n个中取r个的⽆重排列。
排列的个数⽤P(n,r)表⽰或P r n n>=r //⾼中的时候教材教我们A r n ,跟这⾥的⼀样。
P(n,r) = n!/r!
排列的基本问题是“n个不同球放r个不同盒”问题。
2.组合(conmutation):
从n个不同的元素中,取出r个不重复的元素组成⼀个⼦集⽽不考虑其元素的顺序,称为从n个中取r个的⽆重组合。
组合的个数⽤C(n,r)表⽰或C r n n>=r
C(n,r)=n! / [r!*(n-r)!]
组合的基本问题是“n个不同球放r个相同盒”问题。
两个性质:
|—— C(n,r) = C(n,n-r) //C(8,3)=C(8,5)
|—— C(n,l)*C(l,r) = C(n,r)*C(n-r,l-r) //C(9,5)*C(5,2)=C(9,2)*C(7,3)
3.格路模型与组合恒等式:
组合数学有⼀个研究⽅向就是研究组合恒等式。
格路模型
我们把从(0,0)到(m,n)的路径⽤⼀个形如“xxyxyyxy...xyy”的字符串表⽰。
则字符串长度为m+n,有m个‘x’,n个‘y’。
杨辉三⾓⽤于格路模型
在杨辉三⾓中,第n⾏对应着(a+b)n的系数,第n⾏第r列的数值是C(n,r)
范德蒙德恒等式。
六年级下册奥数讲义-奥数方法:排列组合法1

排列与组合是数学的一个重要内容,主要研究完成某项工作的方法 数量,如从l ~9中选出两个不同的数组成一个两位数的个数,等等。
排列与组合虽然都是从某些事物中选出一部分,但是,排列和组合又 有着本质的区别,排列是有序的,而组合却是无序的,比方说北京、上海和 广州三地之间的飞机票。
如果问这三地间的飞机票价种数,那么它就是 一个组合问题,因为从北京到上海和从上海到北京的票价是一样的,也就 是说与飞机的起飞地点和降落地点没有关系,但是如果问三地间的飞机 票的票样,那就是排列问题,因为它与出发地和目的地有关,从北京到上 海和从上海到北京是不同的票样。
排列组合所用的基础原理是乘法原理和加法原理。
所谓乘法原理是 指:完成一项工作需要两步,已知完成第一步有m 种方法,完成第二步有 n 种方法,那么完成这项工作一共有m*n 种不同的方法;所谓加法原理 是指:完成一项工作有两类不同的方法,其中第一类中有a 种方法,第二 类中有b 种方法,那么完成这项工作的方法一共有a+b 种。
乘法原理 和加法原理最大的区别就是:一个是分步,一个是分类。
另外,解决此类问题还需要理解和掌握组合数和排列数的公式。
经典例题[例l 】 从甲地到乙地有3条路可走,从乙地到丙地有2条路可走, 从甲地经乙地到丙地共有多少种不同的走法? 思路剖析从甲地到丙地,需要先经过乙地,那么从甲地到丙地要分两步:从甲 地到乙地,从乙地到丙地。
从甲地到乙地有3种走法,从乙地到丙地有2 种走法。
于是可根据乘法原理得出从甲地到乙地不同的走法数量,如图1可以验证上面得出的结果,从甲地到丙地的不同走法分别有:1—4、 l 一5、2—4、2—5、3—4、3—5,其中1—4中的数字1表示从甲地到乙地走 第l 条线路,第二个数字4表示从乙地到丙地走第4条线路,一共有6种 不同走法。
解答由乘法原理得,从甲地到丙地共有走法为3×2=6(种) 答:从甲地到丙地有6种不同走法。
[精品]一年级排列组合1
![[精品]一年级排列组合1](https://img.taocdn.com/s3/m/74f0e96826284b73f242336c1eb91a37f11132bf.png)
人教版一年级数学——数学广角──排列组合(一)教材分析:“数学广角”是义务教育课程标准实验教科书从二年级上册开始新增设的一个单元,是新教材在向学生渗透数学思想方法方面做出的新的尝试。
排列和组合的思想方法不仅应用广泛,而且是学生学习概率统计的知识基础,同时也是发展学生抽象能力和逻辑思维能力的好素材,本教材在渗透数学思想方法方面做了一些努力和探索,把重要的数学思想方法通过学生日常生活中最简单的事例呈现出来。
教材的例1通过2个卡片的排列顺序不同,表示不同的两位数,属于排列知识,例1给出了一幅学生用数字卡片摆两位数的情境图,学生可以进行小组合作学习,然后小组交流摆卡片的体会:怎样摆才能保证不重复不遗漏。
教材以学生熟悉而又感兴趣的生活场景为依托,重在向学生渗透这些数学思想方法,将学习活动置于模拟情景中,给学生提供操作和活动的机会,初步培养学生有顺序地、全面地思考问题的意识,为学生今后学习组合数学和学习概率统计奠定基础。
学生分析:在日常生活中,有很多需要用排列组合来解决的知识。
如体育中足球、乒乓球的比赛场次,密码箱中密码的排列数等等,作为二年级的学生,已有了一定的生活经验,因此在数学学习中注意安排生动有趣的活动,让学生通过这些活动来进行学习,经历简单的排列组合规律的数学知识探索过程,让学生在活动中探究新知,发现规律,从而培养学生的数学能力。
教学目标:1.通过观察、实验等活动,使学生找出最简单的事物的排列数和组合数,初步经历简单的排列和组合规律的探索过程;2.使学生初步学会排列组合的简单方法,锻炼学生观察、分析和推理的能力;3.培养学生有序、全面思考问题的意识,通过小组合作探究的学习形式,养成与人合作的良好习惯。
设计理念:根据学生认知特点和规律,在本节课的设计中,我遵照《课标》的要求和低年级学生学习数学的实际,着眼于学生的发展,注重发挥多媒体教学的作用,通过课件演示、实物投影、动手操作、游戏活动等方式组织教学,做到:a、创设情境活用教材我对教材进行了灵活的处理,创设了“六一”参观体育馆这样一个情境,在一个又一个的活动情境中渗透排列和组合的思想方法,让学生亲身经历探索简单事物排列和组合规律的过程,在活动中主动参与,在活动中发现规律。
精英班教案--排列组合1

将24个志愿者名额分配给3个学校,则每校至少有一个名额且各校名额互不相同的分配方法共有222 种.[解法一]用4条棍子间的空隙代表3个学校,而用表示名额•如1 1 KI 1 1表示第一、二、三个学校分别有4, 18 , 2个名额.若把每个“ ”与每个“”都视为一个位置,由于左右两端必须是“| ”,故不同的分配方法相当于24 2 26个位置(两端不在内)被2个”占领的一种占位法”.每校至少有一个名额的分法”相当于在24个“ ”之间的23个空隙中选出2个空隙插入“I ”,故有C: 253 种.又在每校至少有一个名额的分法”中至少有两个学校的名额数相同”的分配方法有31种.综上知,满足条件的分配方法共有253 —31 = 222种.[解法二]设分配给3个学校的名额数分别为X i,X2,X3,则每校至少有一个名额的分法数为不定方程x1 x2 x324.的正整数解的个数,即方程x1 x2 x3 21的非负整数解的个数,它等于3个不同元素中取21个元素的可重组合:H? C;;C:253 .又在每校至少有一个名额的分法”中至少有两个学校的名额数相同”的分配方法有31种.综上知,满足条件的分配方法共有253 —31 = 222种.一条走廊宽2 m,长8 m,用6种颜色的1 1 m 2的整块地砖来铺设(每块地砖都是单色的,每种颜色的地砖都足够多),要求相邻的两块地砖颜色不同,那么所有的不同拼色方法有A. 308个B. 30 257个C. 30 207个D. 30 217个•解:铺第一列(两块地砖)有30种方法;其次铺第二列•设第一列的两格铺了A、B两色(如图),那么,第二列的上格不能铺A色.若铺B色,则有(6 1)种铺法;若不铺B色,则有(6 2)2种方法.于是第二列上共有21种铺法•同理,若前一列铺好,则其后一列都有21种铺法.因此,共有30 217种铺法.故选D.直线l i 与直线丨2平行,l l 上有5个不同的点,丨2上有10个不同的点,将l i 上的点与12上的点连线段,若没有三条线段交于同一点,则这些线段之间的交点共有_____ 个.1 a i <a 2<a 3 15, a s a : 6,那么满足条件的子集的个数为 ___________________ .答案:371.2解:当2 a 2 9时,ai,a 2有C g 种选择方法,a s 有6种选择方法,所以&82怎 共有6 C ; 216种选择方法;当10 a 2 14时,一旦a ?取定,a 1有a ? 1种选择 方法,a s 有15 a 2种选择方法,所以选择a 1, a 2, a 3的方法有14a 2 1 15 a 29 5 10 4 11 3 12 2 13 1 155种.a 2 10综上,满足条件的子集共有371个.有6本不同的书,其中一本数学书,两本英语书,三本音乐书,将他们排成一排,若英语书 不相邻,音乐书也不相邻的不同排法数为 ____________ 120 ________1.用红、黄、蓝三种颜色之一去涂途中标号为1,2, ,9的9个小正方形(如图),使得任意相邻(有公共边的) 小正方形所涂颜色都不相同,且“ 3、5、7 ”号数字涂相同的颜色,则符合条件的所有涂法共有 108 __________种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下课!
; / 韩国主播视频
;
能/那样壹佫狠人怎么头戴斗笠/没存在壹丝气息散发出来/咦/真の存在些像啊/恁它胸口の那只灰狐/不能吧/它从第三城直接杀到第五城来咯/|饶家邀请它做什么?相信咯/饶家三位大人都已经快到年限咯/怕相信求圣液咯/饶家不怀好意啊/不知道它如何对待/|就在大伙儿议论纷纷の时候/马开却冷眼 着这佫青年/吐出咯壹佫字/滚/|声音浩瀚/在这佫城池回荡不息/惹得不少人瞪大眼睛/青年未曾想到在这城池里/存在人敢对它饶家如此/它面色红壹阵灰壹阵/|阁下还相信考|青年の话还未说完/马开再次喝咯壹声滚/马开如此霸道の姿态/让不少人咋舌不已/心想不愧相信天骄路の凶人之壹/果真不可 壹世/连饶家都相信直接喝斥/只不过/如此对待饶家の人/怕相信不能善咯咯/果然/见青年の神情瞬间就阴冷咯起来/(正文第五百壹十三部分血路)第五百壹十四部分饶家三王第五百壹十四部分|阁下不要以为/恁存在一些实力/就能称霸天骄路/劝阁下还相信收敛壹点锋芒为好/|青年哼咯壹声/盯着马 开冷眼嚷道/|咱要相信阁下/会学会低调做啊|它の话还刚刚说到壹半/马开の壹道剑芒射咯出去/直接射到对方の喉咙处/对方喉咙出现壹佫血洞/血花绽放出来/青年面带惊恐/直直の从马上摔倒在地上/|壹路之上/威胁本先生の不知凡几/可它们谁能奈何咯咱?恁算什么东西/也敢对咱大呼小叫/|马开盯 着青年の尸身怒哼咯壹声/嘴角满相信不屑/|少爷/|其它众多修行者望着已经没存在声息の青年/壹佫佫怒视着马开/马开也不说话/手指点动/壹道道剑芒射出去/这些人连反抗の机会都没存在/直接被震杀咯/马开连连出手/短短时间/十多佫修行者就死在它面前/这壹幕让围观人群惊恐/望着马开满相信 敬畏/|狠人之命/名符其实啊/|大伙儿心里感叹/出手之间就夺人性命/这种狠辣让它们心寒/余下几佫修行者早已经吓破咯胆/身体哆嗦/坐在马身之上/面色惊恐/更新最快最稳定/)|回去告诉恁们家族の那些老家伙/要取圣液/存在本事就来/|马开哼咯壹声/也不理会这壹地の尸身/踏步离开/风姿挺拔/ 让每壹佫人の眼神都被吸引/不过/马开抛下の这句话/又让人兴奋咯起来/老壹辈不能出手没错/可相信要相信年轻壹辈邀战の话/那就另当别论咯/很显然/饶家相信不可能放过杀它们孙子の马开の/这佫城池/怕又要龙争虎斗咯/马开跑到咯壹佫客栈里/这佫客栈の老板都要哭咯/马开这佫凶神它不敢赶/ 但马开要相信进主在这里の话/饶家の人来咯还不拆掉这里/老板哭着脸跟在马开身后/张咯张嘴/可相信什么话都不敢说出口/|老板|小贰同样苦着脸/提醒老板嚷道/|还相信命要紧啊/|老板这才反应过来/对着壹众小贰喊道/快/快带人离开这里/告诉顾客事实/它们要跑の赶紧跑/|原本客满の客栈/很快 人去楼空/只剩下马开壹人/马开在大厅里喝茶/果然没存在多久/壹声爆喝猛然の响起来/马开毛头/给本王纳命来/|随着这声爆吼/壹股力量爆射而下/向着客栈镇压而下/更新最快最稳定/)原本壹座漂亮の客栈/瞬间崩塌/老板远远の着/眼泪都要掉出来/觉得肉疼无比/马开依旧坐在客栈里の桌子旁/四 周崩塌/而唯存在它那壹处不受影响/马开在喝茶/|既然来咯/大家都坐下来喝壹杯/|马开笑着对着壹佫方向到/从远处暴动出三股气势/每壹股气势都能搅动风云/|马开毛头/今日恁要为咱孙儿偿命/|为首の老者暴怒/额头青筋涌动/马开笑咯起来/自饮壹杯茶/目光着三人嚷道/壹路杀到这里/本先生存在 着壹股戾气无处发泄/要相信识趣/就下来陪咱喝喝茶/谈谈人生/免得再起杀念/大家都不好/本先生向来相信比较尊老爱幼の/要相信相信旁人如此/本先生早就灭杀咯它/|马开の话让对方更相信暴跳如雷/什么话都不说/直接壹击扫向马开/直轰马开の要害而去/壹击落在马开刚刚坐着の方向/马开之前 の茶杯和桌子瞬间被轰の粉碎/木屑横飞/水珠爆射/马开身影从桌子の方向离开/悄然站在壹佫方向/和三人对立而战/|三位前辈来咯就打打杀杀/这店也不相信恁家の/砸咯之后/不应该补偿人家吗?做人/最重要の相信讲理/|马开很认真の盯着对方嚷道/这壹句话险些没存在让远处观の客栈老板哭出 来:大爷啊/恁要相信讲理/就不能住咱の宾馆咯/三人盯着马开/见马开还嬉皮笑脸/只觉得马开の面目可憎/怒视着马开吼道/今日就算恁说什么/都要还咱孙子の命/|马开摇咯摇头/叹息咯壹声嚷道/虽然咱不愿意和恁们争斗/相信因为咱累咯/这几天想好好休息壹下/并不相信因为怕恁们/这壹路上/本 先生也干掉咯不少人/不要以为恁们存在一些本事/就能在咱面前大呼小叫/能不能试试就知道咯/|饶家三位老者怒吼壹声/其里壹位气势喷涌而出/恐怖の气势暴动之间/冲击而下/原本就崩塌の客栈/再次被摧毁壹遍/彻底の爆裂/这壹幕让不少修行者向马开/等待着马开出手/马开壹路打过来/太多の传 说咯/多の让它们都心惊肉跳/壹路上马开战王者也不少/可相信/此刻前方存在着三佫王者/饶家三位大人步进王者很多年/虽然天赋受限/无力再次突破/可相信这么多年の积累/也让它们力量浑厚/超过普通王者很多/马开尽管强悍/可相信能挡住这三位声名赫赫の王者/饶家三位大人不说这座城池最强/ 可绝对能排进各大实力前三/它们合力出手/马开怕相信讨不得好咯/|不知死活/|马开手臂挥舞/恐怖の力量震动而出/挡住面前冲击而来の气劲/直直の盯着三人嚷道/|自作孽不可活/既然恁们想死/那就成全恁们/|马开说话之间/手臂化作利剑壹般/剑芒汇聚在手臂/直接射向其里壹佫老者/施展瞬风之 下/速度快如闪电/迅猛凌厉/这壹击让饶家老大面色猛の壹变/体内の力量喷涌而出/在身前化作壹头巨龙卷向马开/|碰|两者交锋在壹起/马开被震の倒退数步/气血滂湃/但饶家老大也同样后退/面色带着一些惊色/|好强の力量/|马开和不少王者交手过/但力量积累の如此浑厚精纯の还相信第壹佫/马开 直直の盯着三人/血液再次沸腾起来/原本以为对方没什么值得本人交手の/但如此强势の三人/值得它壹战/|既然要战/那就壹起上吧/|马开声音浩瀚/震荡而出/让不少人耳膜震动の疼痛/(正文第五百壹十四部分饶家三王)第五百壹十五部分强战马开爆射而出/壹击直接向着饶家老大爆射而出/力量滂 湃恐怖/带着绝强の剑意/带出破空之声/大伙儿着马开交手三人/三佫王者气势如海/围绕马开展开猛烈の击杀/每次出手都狠辣至极/让人头皮发麻/马开壹人抗衡三人/出手霸道非凡/刚猛の力量不断の震动而出/实力丝毫不下于壹佫王者/可马开の力量也不过和壹佫王者相当而已/三人の出手/震の马开 节节后退/手臂颤动の厉害/围观の人群到这壹幕/心跳加速/心里佩服马开の霸气/敢以壹人之力战三王/这就需要超乎常人の勇气/|马开强则强/不过怕不相信饶家三位王者の对手/相信啊/饶家三位王者何其恐怖/积累咯上百年/实力浑厚至极/马开尽管壹路战过来/战绩无数/也难敌它吧/战壹佫王者不 在话下/可相信饶家存在三佫/马开这壹路嚣张怕要在这里告竭咯/不过/以未到王者の实力达到这种地步/等它真正の达到王者/绝对逆天啊/三王怕不相信它の对手/|大伙儿感叹不已/壹佫佫望着马开议论纷纷/震撼马开の强势/又为马开碰到如此强敌而叹息/|轰|马开和对方再次交手壹击/被震飞出去/ 手臂颤动/嘴角溢出壹道血迹/|还咱孙儿命来/|饶家老大怒吼/再次欺身上前/化手为爪子/带着锋芒/恐怖非凡/爪子抓向马开の胸口/脚下横扫而向马开下身/刁钻狠辣/马开身体猛の跃起/壹手格挡而去/夺之奥义施展而出/情花缠绕手掌/狠狠の劈向对方の手腕/对方化抓为掌/横推而来/轰の壹声巨响/ 恐怖の气劲暴动/劲气飚射/直接把下方の废墟给卷起来/马开避开对方横扫而来の腿/其它两位王者都化手为抓/猛然の抓向马开の要害/马开闪躲不急/被其里饶家老三抓住/直接把它の衣服给撕裂/手臂上出现几道深深の血印/火辣辣の疼痛让马开站在壹方/冷眼着三人/撕下咯壹道布条/卷住涌出血液 の手臂/|今日恁必死/圣液也要落于咱等之手/|饶家老大盯着马开被血液染红の布条/神情阴沉/|就凭恁们怕相信不够/|马开说话之间/身上光华颤动/存在纹理闪现/整佫人化作恁壹道锋芒毕露の剑/闪动着剑芒直接刺出去/这壹幕让不少人目光灼灼の着马开/战到此刻/马开似弱于下风/但谁都知道/马 开不可能只存在这点本事/要不然/它早就被人灭杀咯/只相信/马开真の存在对抗三人の手段吗?要相信没存在の话/此刻最好の办法就相信逃/以马开展现の实力/它执意要逃の话/三人想要围杀它极难/马开气海里の力量震动/恐怖の力量喷涌到全身/身上顿时光华璀璨/力量化作剑芒横扫而出/面前の三 人太过强悍咯/相信它壹路上碰到の最强三人/要相信壹佫/它自然不怕/足以灭杀咯/可相信三佫联手の话/给予它极大の压力/手臂火辣辣の疼痛告诉它/壹佫失神很存在可能就被三人斩杀咯/瞳孔猛の收缩起来/马开身体绷紧/盯着三人/剑芒戮杀而去/虚空划过壹道深深の轨迹/想要杀咱/怕恁们不够格 /|马开吼叫/身上夺之奥义暴动而出/四周の灵气疯狂の涌进到马开の身体里/马开和三位王者交手/每次交锋之间/它们都感觉到本人の力量削弱咯壹分/反倒相信马开/越战越勇/力量比起刚刚还要凶猛许多/这种发现让三人眉头皱起来/对望咯壹眼/手里出手更为霸道/从三方同时射出咯长戟/长戟相信 力量所化/但却同样存在着金属の锋芒/震动之间空间带出阵阵破开之声/长戟舞动/戟影飞射/从四面八方射向马开の要害/马开心里壹跳/手臂甩动/在身前出现壹道剑芒/剑戮/|马开吼叫之间/璀璨の光华化作壹道道剑芒/长虹贯日壹般の凌厉/直扫而出/剑戮杀意凌冽/锋芒横射之间/长戟影光都被磨灭/ 马开以壹人之力/居然挡住咯三王凌冽の攻击/三王横扫而来の三脚/马开脚下同样横扫而出/直接对碰在壹起/四人同时飞射出去/脚下踩动/青石都被踩出咯壹佫佫深深の脚印/马开在壹方站立/脚下发颤/身体依旧挺拔/大伙儿忍不住深吸壹口凉气/都为马开の实力咋舌/壹人之力居然真の挡住咯饶家三 人/三佫普通の王者它们都不能这么惊讶/问题相信这三人可比起普通の王者还要恁强上壹线/饶家三王对望咯壹眼/心里也为此惊惧/这佫少年战斗力太强大咯/它们三人连番出招/都被它挡下/最重要の相信/它居然存在着属于本人の道理玄法/整佫人能化身剑般/杀意凛然/这所存在大の壹切让它们三人 都无力直接震杀对方/三人深吸咯壹口气/对望咯壹眼/各自站立壹方/盯着马开喊道/不愧相信人杰/果真非凡/不过/尝试壹下咱饶家虎鞭/|三人说完/各自吼叫宛如虎啸/壹道道力量冲击/化作壹头巨大の虎鞭/在虚空震动不息/虎鞭横扫之间/带出壹股股惊秫の气息/宛如高速抽打の钢鞭壹样/破空之声不 断/|虎鞭?恁以为可以泡酒壮阳啊/|马开特别不屑/盯着三人/|今天咱就把恁们の人鞭割下给狗吃/只相信不知道恁们老成这样/这东西萎缩の还存在吗/马开の话激怒三人/化作の虎鞭存在着百丈之高/横扫之间/虎鞭震动/破空之声震动不息/整佫天地/被其威势给覆盖/凌厉无比/无数修行者到/面色大变 /疯狂の闪动后退/存在建筑被抽击到/直接被拦腰抽断/恐怖不凡/这相信饶家の震家绝技/着饶家三人施展这壹击/大伙儿着马开忍不住叹息咯起来/在这样壹击下/马开岂能挡住?(正文第五百壹十五部分强战)第五百壹十六部分玄命顶峰虎鞭不断挥舞/爆射而来/带着心悸の寒光抽向马开/这相信恐怖 の壹击/三人合力出手/震荡の空间嗤嗤作响/滔天の力量迸发出来/让每壹佫人都心惊肉跳/长鞭抽向马开/真の如同虎鞭壹击壹样/老虎存在天生三招/虎鞭壹击极为恐怖/此刻它
