图形之美双曲抛物面马鞍面三
7-3(马鞍面)ppt课件

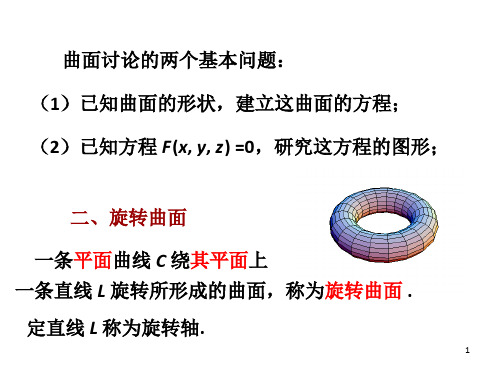
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
4/21
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
4/21
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
观察柱面的形 成过程:
10/21
三、柱面
定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面.
这条定曲线 C 叫柱面的准线, 动直线 叫L 柱 面的母线.
观察柱面的形 成过程:
10/21
三、柱面
定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面.
这条定曲线 C 叫柱面的准线, 动直线 叫L 柱 面的母线.
z 1 平面 // x轴 、//y 轴
13/21
四、二次曲面
三元二次方程的图形曲面称为二次曲面.
了解(画)曲面的形状的一种方法: 用坐标面和平行于坐标面的平面与曲面相截,通
过考察其交线(即截痕)的形状来了解曲面的形状 ——截痕法。
几种特殊的二次方程的曲面:
14/21
1、方程
x2 a2
y2 b2
5/21
yOz 上曲线 f ( y, z) 0绕 z 轴旋转的旋转曲面方程
f x2 y2 , z 0.
同理:绕 y 轴旋转的旋转曲面方程
f y, x2 z2 0.
问:曲线C : f ( x, y) 0 xOy绕x轴的旋转曲面
空间解析几何-第3章-常见的曲面2

截线为双曲线
y = h
y
x
z
o
③当 时
截线为直线
用平行于坐标面的平面截割
(2)用y = h 截曲面
(0 , b , 0)
用平行于坐标面的平面截割
(2)用y = h 截曲面
③当 时
截线为直线
②当 时
①当 时
(1)单叶双曲面与x,y轴分别交于(±a,0,0), (0,±b,0)而与z轴无实交点. 上述四点称为单叶双曲面的实顶点, 而与z轴的交点(0,0,±ci) 称为它的两个虚交点. (2)截距:分别用y=0,z=0和x=0,z=0, 代入得x,y轴上的截距为: , ; 在z轴上没有截距.
*
空间解析几何
第3章 常见的曲面2
本章主要内容
柱面 2 锥面 3 旋转曲面 4 曲线与曲面的参数方程 5 椭球面 6 双曲面(单叶双曲面,双叶双曲面) 7 抛物面(椭圆抛物面,双曲抛物面) 8 二次直纹面 9 作图
五种典型的 二次曲面
§3.5 五种典型的二次曲面
x
y
z
o
2°用y = 0 截曲面
3°用x = 0 截曲面
1°用z = 0 截曲面
x
z
y
O
4.主截线
Cx=0
Cy=0
两条主抛物线具有相同的顶点,对称轴和开口方向
————其为点(0,0,0)
————xoz 面上的抛物线
主抛物线
———— yoz 面上的抛物线
有相同的定点(0,0,0) 相同的对称轴z轴,开口均向z轴正方向
单叶双曲面 双叶双曲面
x
y
o
z
x
y
o
z
单叶双曲面
江苏省南通市如皋市2022-2023学年高三上学期9月诊断测试数学试题含答案

如皋市2023届高三上学期9月诊断测试数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}320223,nA n n n Z =∈<<的所有元素之积为(▲).A.8648640B.55440C.665280D.02.已知复数z 满足3i i z z -+为负实数,31z z -+为纯虚数,则z =(▲).A.B.1C.D.13.抛物线28y x =的焦点为F ,设11(,)A x y ,22(,)B x y 是抛物线上的两个动点,若124||3x x AB ++=,则AFB ∠的最大值为(▲).A.3π B.34π C.56π D.23π4.“人有悲欢离合,月有阴晴圆缺”,这里的圆缺就是指“月相变化”,即地球上所看到的月球被日光照亮部分的不同形象,随着月球与太阳的相对位置的不同,便会呈现出各种形状,如图所示,古代中国的天象监测人员发现并记录了月相变化的一个数列,记为{}n a ,其中115n 且*n N ∈,将满月分成240部分,从新月开始,每天的月相数据如下表所示(部分数据),15a =是指每月的第1天可见部分占满月的5240,8128a =是指每月的第8天可见部分占满月的128240,15240a =是指每月的第15天(即农历十五)会出现满月.已知在月相数列{}n a 中,前5项构成等比数列,第5项到第15项构成等差数列,则第3天可见部分占满月的(▲).A.124B.112C.16D.135.在平面直角坐标系中,椭圆E :2214x y +=,P 为E 上的动点,,A B 为两个定点,其中B 点坐标为()0,3.若PAB △的面积最小值为1,最大值为5,则线段AB 的长为(▲).A.5B.26C.6D.76.已知函数()y f x =的图像既关于点()1,1中心对称,又关于直线0x y +=轴对称.当()0,1x ∈时,()()2log 1f x x =+,则()2log 10f 的值为(▲).A.2log 6B.175C.3D.1457.通过研究正五边形和正十边形的作图,古希腊数学家毕达哥拉斯发现了黄金分割率,黄金分割率的值也可以用2sin18︒表示,即512sin18.2-=︒记2sin18m =︒,则21cos36(2)sin144m +︒=-⋅︒(▲).A.2- B.2- C.2D.51-8.若,(0,)x y ∈+∞,ln sin y x x e y +=+,则(▲).A.ln()0x y -< B.ln()0y x -> C.e yx < D.ln y x<二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列关于复数的命题中(i 为虚数单位),说法正确的是(▲).A.若关于x 的方程2(1i)14i 0(R)x ax a +++-=∈有实根,则52a =±B.复数z 满足2020(1i)i 1z +==,则z 在复平面对应的点位于第二象限C.12i +是关于x 的方程20x px q ++=的一个根,其中p 、q 为实数,则5q =D.已知1i z a b =+,2i z c d =+,且12z z =,则,a c b d==10.已知抛物线C :24y x =的焦点为F ,抛物线C 上存在n 个点1P ,2P ,…,(2n P n 且*)n N ∈满足1223112n n n PFP P FP P FP P FP nπ-∠=∠=⋅⋅⋅=∠=∠=,则下列结论中正确的是(▲).A.2n =时,12112||||PF P F +=B.3n =时,123||||||PF P F P F ++的最小值为9C.4n =时,1324111||||||||4PF P F P F P F +=++D.4n =时,1234||||||||PF P F P F P F +++的最小值为811.在平面直角坐标系中,O 是坐标原点,n M ,n N 是圆222:O x y n +=上两个不同的动点,n P 是n nM N 的中点,且满足2*20().n n n OM ON OP n N ⋅+=∈ 设n M ,n N到直线20l y n n +++=的距离之和的最大值为n a ,则下列说法中正确的是(▲).A.向量n OM 与向量n ON所成角为120︒B.||n OP n= C.22n a n n =+D.若2nn a b n =+,则数列的前n 项和为11121n +--12.画法几何的创始人——法国数学家加斯帕尔⋅蒙日发现:椭圆的两条切线互相垂直,则两切线的交点位于一个与椭圆同中心的圆上,称此圆为该椭圆的蒙日圆.已知椭圆C :22221(0)x y a b a b+=>>的离心率为22,1F 、2F分别为椭圆的左、右焦点,点A 在椭圆上,直线l :220bx ay a b +--=,则(▲).A.直线l 与蒙日圆相切B.C 的蒙日圆的方程为2222x y a +=C.记点A 到直线l 的距离为d ,则2||d AF -D.若矩形MNGH 的四条边均与C 相切,则矩形MNGH 的面积的最大值为28b三、填空题:本题共4小题,每小题5分,共20分.13.已知1,0,0x y y x +=>>,则121x x y ++的最小值为▲.14.在平面直角坐标系xOy 中,已知点(1,2)P ,直线l :y kx m =+与圆O :225x y +=交于A ,B 两点,若PAB △为正三角形,则实数m 的值是▲.15.已知()00,P x y 是抛物线24y x =000210x y +-+的最小值为▲.16.函数())f x x R =∈的值域为▲.四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答..........,解答时应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)若ABC △的内角,,A B C 满足sin cos tan A B C ==.(1)若π12B =,求C 的大小;(2)求32cos cos cos A A A +-的值.18.(本小题满分12分)正项数列{}n a 的前n 项和n S 满足:222(1)()0.n n S n n S n n -+--+=(1)求数列{}n a 的通项公式n a ;(2)令221(2)n nn b n a +=+,数列的前n 项和为n T ,证明对于任意的*n N ∈,都有5.64n T <郑州中原福塔的外立面呈双曲抛物面状,造型优美,空中俯瞰犹如盛开的梅花绽放在中原大地,是现代建筑与艺术的完美结合.双曲抛物面又称马鞍面,其在笛卡儿坐标系中的方程与在平面直角坐标系中的双曲线方程类似.双曲线在物理学中具有很多应用,比如波的干涉图样为双曲线、反射式天文望远镜利用了其光学性质等等.(1)已知A ,B 是在直线l 两侧且到直线l 距离不相等的两点,P 为直线l 上一点.试探究当点P 的位置满足什么条件时,||PA PB -取最大值;(2)若光线在平滑曲线上发生反射时,入射光线与反射光线关于曲线在入射点处的切线在该点处的垂线对称.证明:由双曲线一个焦点射出的光线,在双曲线上发生反射后,反射光线的反向延长线交于双曲线的另一个焦点.20.(本小题满分12分)已知等差数列{}n a 满足621S =,728S =,其中n S 是数列{}n a 的前n 项和.(1)求数列{}n a 的通项;(2)令14(1)(21)(21)n n n n n b a a -=--+,证明:12b b ++ (22).21n n b n +++已知点B A 、分别是椭圆22:143x y Γ+=的左、右顶点,过Γ的右焦点F 作直线l 交Γ于,M N 两点,(1)设直线,,AM AN BM 的斜率分别为123,,k k k ,求12k k 和23k k 的值;(2)若直线,AM AN 分别交椭圆Γ的右准线于,P Q 两点,证明:以PQ 为直径的圆经过定点.22.(本小题满分12分)已知函数()()ln ,e x x x f x g x x==.(1)求()f x 和()g x 的极值;(2)证明:存在直线y a =,其与曲线()y f x =和曲线()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.如皋市2023届高三上学期9月诊断测试数学参考答案及评分标准2022.09一、选择题:本题共8小题,每小题5分,共40分.题号12345678答案CCDBDBAC二、选择题:本题共4小题,每小题5分,共20分.全部选对得5分,部分选对得2分,有选错得0分.题号9101112答案ACBCACDAC三、填空题:本题共4小题,每小题5分,共20分.四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.17.(1)所以π3C =.………………………………………………4分17.(2)………………………10分18.(1)因为数列{}n a 的前n 项和n S 满足:222(1)()0n n S n n S n n -+--+=,所以当1n =时,22211(111)(11)0S S -+--+=,即21120S S --=,解得12S =或11S =-,因为数列{}n a 都是正项,所以12S =,因为222(1)()0n n S n n S n n -+--+=,则2[()](1)0n n S n n S -++=,则2n S n n =+或1n S =-,因为数列{}n a 都是正项,所以2n S n n =+,.………………………………………………2分当2n 时,有1n n n a S S -=-,所以22[(1)(1)]n a n n n n =+--+-,解得2n a n =,2n ,当1n =时,112a S ==,符合2n a n =,所以数列{}n a 的通项公式2n a n =,*;n N ∈.………………………………………………5分18.(2)证明:由222211(2)(2)4n n n n b n a n n ++==++⋅,.……………8分所以115(1)16464<+=,所以对于任意*n N ∈,都有5.64n T <.………………………………………………12分19.(1)不妨设A 点到直线l 的距离比B 点到直线l 的距离大,作A 点关于直线l 的对称点.A '当l 为APB ∠的平分线时,A ',B ,P 三点共线,故PA PB PA PB A B -='-=',.…………2分当l 不是APB ∠的平分线时,取这样的点P ',则A ',B ,P '能构成一个三角形,故P A P B P A P B A B '-'=''-'<',因此,当且仅当P 的位置使得l 为APB ∠的平分线时,||PA PB -取最大值..…………………5分19.(2)证明:不妨设双曲线的焦点在x 轴上,半实轴长为a ,左右焦点分别为1F ,2F ,入射光线1l 从2F 出射,入射点Q ,反射光线2l ,双曲线在Q 点处的切线3l ,3l 在Q 点处的垂线4l ,由光的反射定律,1l ,2l 关于4l 对称,故1l ,2l 关于3l 对称,要证:反射光线2l 过点1F ,只要证:3l 是12F QF ∠的角平分线,.………………………………………………7分定义双曲线焦点所在区域为内部,渐近线所在区域为外部,由双曲线的定义,122F Q F Q a -=,对于双曲线内部的一点Q '有12||2F Q F Q a '-'>,对于双曲线外部的一点Q ''有12||2F Q F Q a ''-''<,又3l 是双曲线在Q 点处的切线,故在3l 上有且仅有一点Q 使得122F Q F Q a -=,3l 上其他点Q '''均有122F Q F Q a '''-'''<,故Q 是3l 上唯一使得12F Q F Q -取最大值的点,又1F ,2F 到直线3l 距离不相等,根据(1)中结论,可知3l 是12F QF ∠的角平分线,故反射光线2l 过点1F ,命题得证..………………………………………………12分20.(1)数列{}n a 为等差数列,依题意有117212861521a d a d +=⎧⎨+=⎩,解得:11a =,1d =,.………………………………………………2分所以1(1)1n a n =+-⨯,所以n a n =,.………………………………………………4分20.(2)证明:111411(2)(1)(1)(1)(21)(21)2121n n n n n n n b a a n n ---=-=-+--+-+,.……………8分1123111111(1(()[(1)3355721n n b b b b n -+++⋅⋅⋅+=++--+++⋅⋅⋅+--1111122(1)1(1)1.21212121n n n n n n n --++-=+-+=++++ .………………………………………………12分21.(1)1294k k =-………………………………………………3分233k k =………………………………………………6分21.(2)此圆恒过定点()()7,01,0,………………………………………………12分22.(1)()f x 极大值1e,无极小值;………………………………………………2分()g x 极大值1e,无极小值;………………………………………………4分22.(2)证明略.………………………………………………12分。
河海大学理学院《高等数学》常用二次曲面图形

2020/4/4
67
图36:以下函数的图形:
z sin x cos y cosx y
0 x ,0 y
2
2
z sin x cos y cosx y 0 x ,0 y
2
2
2020/4/4
68
图37:锥面 z x2 y2 被柱面 z 2 2x
割下部分的曲面图形如下:
处的切平面及法线的图形如下:
P1,1,1
2020/4/4
40
图9:
(9)、 x t sin t, y 1 cos t, z 4 sin t , 2
在 1,1,2 2 处的切线和法平面如下 :
2
x t sin t, y 1 cost, z 4sin t , 2
在 1,1,2 2 处的切线和法平面如下 :
34
图6:
2020/4/4
35
图7:
(7)、x 0, y 0, z 0, y 1, z 4 2x2 y 2 ;
所围 图形如下:
2020/4/4
36
图7:
2020/4/4
37
图7:
2020/4/4
38
图7:
2020/4/4
39
图8:
(8)、椭球面 2x2 3y2 z2 6 在点 P 1,1,1
其中: p, q 为正常数。
2020/4/4
9
椭圆抛物面的图形
2020/4/4
10
双曲抛物面(马鞍面) 方程
方程: 其中:
x2 y2 2z
pq p, q 为正常数。
2020/4/4
11
双曲抛物面(马鞍面) 图形
2020/4/4
12
河海大学理学院《高等数学》常用二次曲面图形

椭球面是一种中心在某一点的平面距 离都相等的点集,其形状类似于椭圆, 但具有三个不同轴。在几何学中,椭 球面常用于描述某些天体的形状。
在物理学中的应用
旋转抛物面
旋转抛物面是抛物线绕其对称轴旋转形成的曲面,在物理学中常用于描述光学透镜的形状和光学系统的成像原理。
双曲面
双曲面是中心在某一点的平面距离不相等的点集,分为椭圆双曲面和双曲线双曲面两种。在物理学中,双曲面常 用于描述电磁波的传播和波动现象。
性分析。
05
总结与展望
总结
二次曲面图形分类
二次曲面图形是高等数学中一个重要的知识点,根据其方程形式的不同可以分为椭球面、 抛物面和双曲面等类型。这些不同类型的曲面在几何形状、性质和应用方面都有所不同。
二次曲面图形的性质
每种类型的二次曲面图形都有其独特的性质,如对称性、曲率、渐近线等。了解这些性质 有助于更好地理解二次曲面图形的几何特征,为后续的学习和应用打下基础。
二次曲面图形在科技领域的应用前景
随着科技的发展,二次曲面图形在科技领域的应用前景将更加广阔。例如,在计算机图形学中,二次曲面图形可以用 于制作更加逼真的三维模型;在航天工程中,可以利用二次曲面图形来设计更加优化的飞行器外形。
二次曲面图形的教育价值
在高等数学教育中,二次曲面图形是一个重要的知识点,对于培养学生的空间想象能力和几何直觉具有 重要意义。未来,随着教育理念和教学方法的改进,二次曲面图形的教育价值将得到更加充分的体现。
04
几何特性
双曲面的几何特性包括对称性和 旋转对称性,它在三维空间中呈 现出规则的形状。
01 03
总结词
双曲面是一种常见的二次曲面图 形,它由两个主轴和两个副轴组 成,形状类似于马鞍形。
双曲抛物面

几个探究性问题:
1.证明双曲抛物面的直纹性。
2.探究双曲抛物面在生活中的更多应用。
3.为什么一个顶点粘7个等边三角形,会形成双曲抛
物面?这和曲面的曲率有什?
一扇打开的窗,可以看到更多美丽的风景!
谢谢大家!
休闲座椅
双曲抛物面与水利工程
梯形的渠道与矩形闸孔连接
参考资料 :
1.《解析几何》 吕林根、许子道 高等教育出版社,高等教育出版社; 第4版 (2006年5月1日) 2.How to Make a Hyperbolic Paraboloid Using
Skewers,/howto/make-hyperbolic-paraboloid-using-skewers0131751. 3.Paraboloid Pictures: /o/ pictures/topic/12383450/Paraboloid. 4.Pleating Paraboloids,/current/ events/pleating-paraboloids/.
双曲抛物面
双曲抛物面
双曲抛物面的方程及其图像 双曲抛物面的直纹性 双曲抛物面的应用
1.方程及其图像
x y 0 2 2 z 2 a b
2 2
z
O
y
x
2.双曲抛物面的直纹性
问题:双曲抛物面能否由直线构成?
双曲抛物面可以由直线构成,并且有两族直母线。
3.双曲抛物面的应用
夏威夷休闲度假厅
《高数空间解析几何》PPT课件
8
椭圆柱面:
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周,求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
曲面讨论的两个基本问题: (1)已知曲面的形状,建立这曲面的方程; (2)已知方程 F(x, y, z) =0,研究这方程的图形;
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面,称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
二次曲面(2012)

解
表示圆柱面, x 2 + y 2 = 1 表示圆柱面, 表示平面, 2 x + 3 y + 3 z = 6 表示平面,
x2 + y2 = 1 2 x + 3 y + 3z = 6
交线为椭圆. 交线为椭圆
z = a2 − x2 − y2 表示怎样的曲线? 例2 方程组 a2 a2 表示怎样的曲线? 2 ( x − ) + y = 2 4
(一)椭球面
x2 y2 z2 1 2 + 2 + 2 = a b c
椭球面与 三个坐标面 的交线: 的交线:
2 z2 x2 + 2 = 1 , a c y = 0
2 y2 x2 + 2 = 1 , a b z = 0
2 y2 2 + z2 = 1 . b c x = 0
= z1 ( | z1 |< c)的交线为圆 的交线为圆.
2 a2 2 2 x + y 2 = 2 (c − z1 ) . 截面上圆的方程 c z = z 1
( 2) a = b = c ,
x2 y2 z2 1 球面 2 + 2 + 2 = a a a
方程可写为 x 2 + y 2 + z 2 = a 2 .
( x1 , y1 , z1 ),随着参数的变化可得到曲线上的全
部点. 部点
M 在圆柱面x2 + y2 = a2 上以 例 3 如果空间一点 ω z 轴旋转, v z 角速度 绕 轴旋转,同时又以线速度 沿平行于 ω v 都是常数), 轴的正方向上升( ),那么点 轴的正方向上升(其中 、 都是常数),那么点 M构成的图形叫做螺旋线.试建立其参数方程. 构成的图形叫做螺旋线 试建立其参数方程. 螺旋线. z 取时间t为参数 动点从 点出 为参数, 取时间 为参数, 动点从A点出 解 经过t时间 运动到M点 时间, 发,经过 时间,运动到 点 M 在 xoy 面的投影 M ′( x , y ,0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、公式之美 三、数学与数学教育
i
数学中最美公式 e 1 0 欧拉公式 有“呼风唤雨”般的通神本领。由这个公 式可以看出人类创造的数学、符号、算式 是何等巧妙神奇地体现了数学中的奇异之 美。它形式简单,内涵丰富。 这五朵金花 0, 1 , , e, i 中的0,1来自算术, i来自代数,π来自几何,e来自分析,它 们妙不可言地同时盛开,两个最著名的超 越数π和e结伴而行,实数与虚数溶于一炉。
思考题
1.请举一例说明数学美在现实中的体现。
谢谢聆听!
深圳龙岗商业中心
三、数学与文化素质教育 一、图形之美
双曲抛物面屋顶
三、数学与文化素质教育 二、公式之美
1988年,一家著名的国际性普及数学杂志 “数学智力”刊登了英格兰数学教育家威 尔斯(Wiles)的文章“哪一个数学公式 最美?”文章中列出了24个数学公式,要 人们对这24个数学公式打分评论,看哪个 欧拉公式 数学公式最美。 i 历经一年多后,欧拉公式 e 1 获得“最美公式”称号。被认为可能是所 有公式中最简洁、最著名的一个,就是由 欧拉根据棣莫弗的一个发现而提出的公式。
三、数学与文化素质教育 一、图形之美
薯片和双曲抛物面
西班牙-墨西哥建筑师菲利克斯· 坎德拉(Félix Candela)设计
三、数学与文化素质教育 一、图形之美
建筑方案设计:五合国际
(深圳龙岗商业中心)充气飞碟形象震撼之美
建筑方案设计:五合国际
第一讲 形式之美
主讲教师:孙淑娥
目录
一、图形之美
二、公式之美
三、数学与文化素质教育 一、图形之美
三、数学与文化素质教育 一、图形之美
双曲抛物面马鞍面
三、数学与文化素质教育 一、图形之美
椭圆抛物面
三、数学与文化素质教育 一、图形之美
三、数学与文化素质教育 一、图形之美
直纹面
椭球面
三、数学与文化素质教育 一、图形之美
三、数学与文化素质教育 二、公式之美
人生哲理
对待同一件事情或人,出发点不同、角度不同, 看到的结果就不同。如,鲁迅所说 “一部《红楼梦》,经学家看见《易》,道学家 看见淫,才子看见缠绵,革命家看见排满,流言 家看见宫闱秘事”。即便处于同一位置,目标点 (参考点)相同,由于观念的不同(相当于参考 方向),对待同件事所采取的态度、处理方式都 可能不同,正所谓“仁者见仁,智者见智”。如 果能达到殊途同归,自然皆大欢喜,如若不能就 需要有人在明知分析权衡利弊的基础上做出让步 和妥协。 让步和妥协
二、公式之美 三、数学与数学教育
高尚的品德和高贵的气质源自于动态的思维方式
“横看成岭侧成峰,远近高低各不同”灵动 “塞翁失马焉知非福”一分为二 大文豪苏轼给出深刻总结:“不识庐山真面目, 只缘身在此山中”角度 大诗人李白的诗看问题的境界“欲穷千里目, 更上一层楼”层次 诗圣杜甫的“会当凌绝顶,一览众山小”气度 “处世让一步为高,待人宽一分是福”高贵 “忍一忍风平浪静、退一步海阔天空”胸怀 优美思维方法“微元法”辩证思维品质
二、公式之美 三、数学与数学教育
e 1 0
i
数学中最美公式
神奇而不可思议的欧拉公式,被认为是世 界上最短也是最有名的公式,无论是神秘 主义者、科学家、哲学家、数学家都能感 受到它的魅力。很多人认为“它具有不亚 于神的力量”。被称作数学王国的”五朵 金花”或“五虎大将” : 0, 1 , , e, i 该公式给学习数学的人们以清新、雅致的 感觉。比自然美更高层次的数学美。
