正弦稳态电路分析和功率计算要点
合集下载
07第七章正弦稳态电路的分析功率部分详解

1
ω
Z
Z R j(ωL 1 )
ωC
当 ω 0
1 即 ω0 L 0C
时
Im[ Z ( j )] 0
•
I
R
jL
•
•
•U I
U
U
Z RR
u
•
电压电流同相位。
U
1
jC
谐振:当满足一定条件(对RLC串联电路,使 ( L=1/ C), 电
路中电压、电流同相,电路的这种状态称为谐振。
串联谐振:
ω
0L
使功率因数提高到0.9 , 求并联电容C。
•
I
+
• P=20kW
U cos1=0.6
C
_
•
•
IL
IC
R
•
U
L 解:
并电容前: Q QL Ptg1
并电容后: Q QL QC
Q Ptg2
C
P U
2
( tgφ1
tgφ2 )
QC Q QL QC CU 2
cosφ1 0.6 得: φ1 53.13 cosφ2 0.9 得: φ2 25.84
有:
•
•
U ZI
•
(R jX ) I
或:
•
•
I YU
•
(G jB)U
复功率 或:
• •
SU I
• •
ZII
(R jX )I 2
• •
SU I
•
U (Y
•
U
)
(G
jB)U
2
R、L、C元件的复功率为:
•
•
SR UR I R
• •
华科电工技术第6章 正弦稳态电路分析 (2)
而且与cos 有关,这是交流和直流的很大区别, 主要由于电
压、电流存在相位差。
cos 1,纯电阻
0,纯电抗
一般地,有 0cos1
X>0, >0,感性, 滞后功率因数 X<0, <0,容性, 超前功率因数
例: cos =0.5 (滞后), 则 =60o (电流滞后电压60o)。
u
C 对电容,i 超前 u 90°,QC<0,故电容发出无功
-
功率。
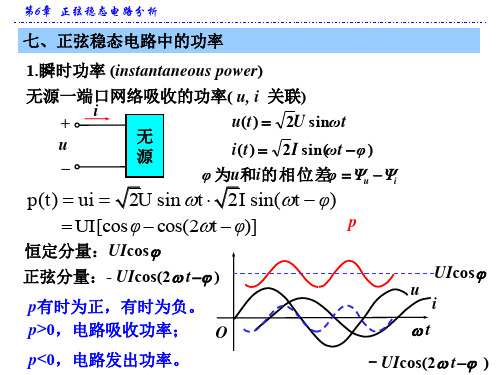
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时,C刚好吸收功率,则与外电路交换功率 为pL+pC。因此,L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
Q,并计算电源的视在功率S和功率因素cos 。
2
解法一: 采用定义计算;
·IS
压、电流存在相位差。
cos 1,纯电阻
0,纯电抗
一般地,有 0cos1
X>0, >0,感性, 滞后功率因数 X<0, <0,容性, 超前功率因数
例: cos =0.5 (滞后), 则 =60o (电流滞后电压60o)。
u
C 对电容,i 超前 u 90°,QC<0,故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时,C刚好吸收功率,则与外电路交换功率 为pL+pC。因此,L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
Q,并计算电源的视在功率S和功率因素cos 。
2
解法一: 采用定义计算;
·IS
第6章 正弦稳态电路的功率

例 求图所示电路电源对电路提供的功率(有功功率)。
3 + 2H – 4 + 1F 8 • I 3 4
j4
– 10 0°
–j4
10 2 cos2tV
解 利用 P = UI cos z 计算,只要算得阻抗 Z 即可, j4(4–j4) Z = 3 + j4+4 –j4 = 3 + 4 + j4 = 7 + j4 = 8.0623 29.74° I = U = 10 = 1.2403 A 8.0623 |Z| P = UI cos z = 10×1.2403×cos 29.74° = 10.77W
+ I
10kW 0.8 (超前) 15kW 0.6 (滞后)
– = 10000 [0.8 – j 1 – 0.82 ] 2300V 0.8 = 10000 – j7500 V•A • S2 = S2[cosZ2+ jsinZ2] = 15000 [0.6 + j 1 – 0.62 ] 0.6 = 15000 + j20000 V•A • S = S1 + S2 = 25000 + j12500 = 27950.85 26.57° V•A
Us2 RL 由此可得 PL = ( Rs+RL)2 第二步,令以上关于RL的导数等于零,或直接引用第四章中的 结论,即: RL = Rs 时,负载上获得的功率最大。 Us2 RL Us2 此时 PLmax = = 2 (2RL) 4RL 总结:当 ZL = RL + jXL = Rs – jXs = Zs* 时(共轭匹配),负载获 得的功率最大。 如果阻抗模值可变而阻抗角不变,那么在满足什么条件下获 得最大功率?
电路分析基础正弦稳态电路的功率

返节目录
电路分析基础
对指标点1-2的贡献: • 掌握正弦稳态功率的基本知识,能够应用基本理论分 析计算正弦稳态功率问题。 对指标点2-2的贡献: • 能够运用电路网络的基本定理,准确描述二端网络的 等效阻抗、阻抗匹配等工程问题。
返节目录
电路分析基础
10.1 二端网络的功率
1、瞬时功率
设端口电压、电流,且 u(t) Um cos(t u )V
S
显然 cos(u i ) 功率因数角:u i
有功功率、无功功率、视在功率的关系:
SQ
S2 P 2 Q2
P
功率三角形
返节目录
电路分析基础
S UI
P UI cos(u i ) Q UI sin(u i )
5、复功率
,
设:U Uu I Ii
定义: S~ UI 伏安(VA)
视在功率: S UI 复功率: S~ UI
返节目录
电路分析基础
测试题2 有功功率、无功功率、视在功率、复功率、 功率因素之间有何联系?
S~ P 2 Q2 S
P Re S
S~ P jQ
P
S
Q Im S
返节目录
电路分析基础
测试题3 填空题
返节目录
电路分析基础
例1 电路如图所示,已知 is (t) 20 cos100tmA 求三条支路的有功功率、视在功率和功率因数。
(2)电容
z 90o
Q UI CU 2 I 2 C
(3)电感 z 90 o
Q
UI
U2
LI 2
(4)若二端网络不含受控源,则 L
Q 网络内各电容和电感元件的无功功率之和。
返节目录
电路分析基础
电路分析基础
对指标点1-2的贡献: • 掌握正弦稳态功率的基本知识,能够应用基本理论分 析计算正弦稳态功率问题。 对指标点2-2的贡献: • 能够运用电路网络的基本定理,准确描述二端网络的 等效阻抗、阻抗匹配等工程问题。
返节目录
电路分析基础
10.1 二端网络的功率
1、瞬时功率
设端口电压、电流,且 u(t) Um cos(t u )V
S
显然 cos(u i ) 功率因数角:u i
有功功率、无功功率、视在功率的关系:
SQ
S2 P 2 Q2
P
功率三角形
返节目录
电路分析基础
S UI
P UI cos(u i ) Q UI sin(u i )
5、复功率
,
设:U Uu I Ii
定义: S~ UI 伏安(VA)
视在功率: S UI 复功率: S~ UI
返节目录
电路分析基础
测试题2 有功功率、无功功率、视在功率、复功率、 功率因素之间有何联系?
S~ P 2 Q2 S
P Re S
S~ P jQ
P
S
Q Im S
返节目录
电路分析基础
测试题3 填空题
返节目录
电路分析基础
例1 电路如图所示,已知 is (t) 20 cos100tmA 求三条支路的有功功率、视在功率和功率因数。
(2)电容
z 90o
Q UI CU 2 I 2 C
(3)电感 z 90 o
Q
UI
U2
LI 2
(4)若二端网络不含受控源,则 L
Q 网络内各电容和电感元件的无功功率之和。
返节目录
电路分析基础
第9章 正弦稳态电路的分析
§9.3 电路的相量图
例1: 应用相量图求图示电路的电压表的读数。
解:RC串联电路, I 设参考相量:= I 00 A I· + 8V + R 画相量图: + 1 · 先画参考相量: 如图(a)所示, U V jwC 11V I, 再画相量 UR , UR 与相量 I 同相, 再画相量 UC, UC 相量滞后 I90º 。 · UR 而 U=UR+UC ·I· 因此得直角三角形,所以 · UC U
1 | Y |= , φz = -φy |Z |
RL串联电路如图,求在w=106rad/s时的等效并 例 联电路。 50W 解 RL串联电路的阻抗为:
X L = w L = 106 0.06 10-3 = 60W
0.06mH
Z = R jX L = 50 j60 = 78.150.20 W
z
但有受控源时,可能会出现
| j z | 90
或
| j y | 90
其实部将为负值,其等效电路要设定受控 源来表示实部;
注意
③一端口N0的两种参数Z和Y具有同等效用,彼 此可以等效互换,其极坐标形式表示的互换 条件为
| Z || Y |= 1
jz j y = 0
6. 阻抗(导纳)的串联和并联 ①阻抗的串联
1 1 Y= = = 0.0128 - 50.20 W Z 78.150.20 = 0.0082 - j0.0098 S 1 1 R = = = 122 W G 0.0082 1 L = = 0.102 mH 0.0098w
R’
L’
注意
①一端口N0的阻抗或导纳是由其内部的参数、结 构和正弦电源的频率决定的,在一般情况下, 其每一部分都是频率的函数,随频率而变; ②一端口N0中如不含受控源,则有 | j y | 90 | j | 90 或
电路设计--正弦稳态电路的功率讲解
2U cos(t u )×
2I cos( t i )
UI cos( u i ) UI cos(2t u i )
u i
为电压和电流之间的相位差
p UI cos UI cos(2t u i )
瞬时功率有两个分量: 第一个为恒定分量,第二个为正弦分量。
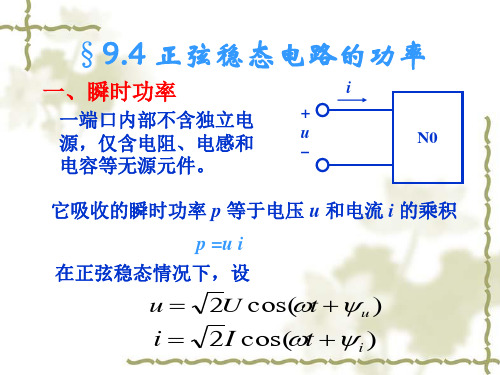
§9.4 正弦稳态电路的功率
一、瞬时功率
一端口内部不含独立电 源,仅含电阻、电感和 电容等无源元件。
+ u i N0
它吸收的瞬时功率 p 等于电压 u 和电流 i 的乘积 p =u i 在正弦稳态情况下,设
u
2U cos( t u )
i
2I cos( t i )
瞬时功率 p= 令
另一种解法
而 R = 30 Ω I R 30 Z R 2 (L) 2
2
故可求得: L 502 302 = 40Ω 40 L = 127 mH
解:
u 10
i 50 2 sin(314t 45 )=50 2 cos(314t 45 )
i 45
故:P UI cos(u i )=300 50cos55 8610(W )
例9-17:测量电感线圈R、L的实验电路,已知电压 表的读数为50V,电流表的读数为1A,功率表读数为 30W,电源的频率f =50Hz。试求R、L之值。
PC=UIcos =UIcos(-90)=0
电容不消耗有功 且QC<0
1 2 QC UI I wCU 2 wC
* 电感、电容的无功功率具有互相补偿的作用
例9-16: 求平均功率P。 已知u, i关联取向,且: u 300 2 cos(314t 10 )(V) i 50 2 sin(314t 45 )(A)
2I cos( t i )
UI cos( u i ) UI cos(2t u i )
u i
为电压和电流之间的相位差
p UI cos UI cos(2t u i )
瞬时功率有两个分量: 第一个为恒定分量,第二个为正弦分量。
§9.4 正弦稳态电路的功率
一、瞬时功率
一端口内部不含独立电 源,仅含电阻、电感和 电容等无源元件。
+ u i N0
它吸收的瞬时功率 p 等于电压 u 和电流 i 的乘积 p =u i 在正弦稳态情况下,设
u
2U cos( t u )
i
2I cos( t i )
瞬时功率 p= 令
另一种解法
而 R = 30 Ω I R 30 Z R 2 (L) 2
2
故可求得: L 502 302 = 40Ω 40 L = 127 mH
解:
u 10
i 50 2 sin(314t 45 )=50 2 cos(314t 45 )
i 45
故:P UI cos(u i )=300 50cos55 8610(W )
例9-17:测量电感线圈R、L的实验电路,已知电压 表的读数为50V,电流表的读数为1A,功率表读数为 30W,电源的频率f =50Hz。试求R、L之值。
PC=UIcos =UIcos(-90)=0
电容不消耗有功 且QC<0
1 2 QC UI I wCU 2 wC
* 电感、电容的无功功率具有互相补偿的作用
例9-16: 求平均功率P。 已知u, i关联取向,且: u 300 2 cos(314t 10 )(V) i 50 2 sin(314t 45 )(A)
正弦稳态的功率要点

其相量图如图(d)所示。单口网络吸收的平均功率为
P UI cos φ 10 2 cos(53.1 ) 12W
此时的功率因数=cos=0.6,功率的利用效率很低。
为了提高功率因数,可以在ab两端上并联一个电容, 如图(b)所示。为分析方便,先将电阻与电感串联等效变换 为电阻和电感的并联,如图(c)所示,其电导和电纳值由下 式确定
能量。
值得注意的是在用UIcos计算单口网络吸收的平均功 率时,一定要采用电压电流的关联参考方向,否则会影响 相位差的数值,从而影响到功率因数cos以及平均功率 的正负。
二、功率因数
从式(9-19)可见,在单口网络电压电流有效值的乘积 UI一定的情况下,单口网络吸收的平均功率P与cos的大 小密切相关,cos表示功率的利用程度,称为功率因数,
时,功率因数角=090以及功率因数cos<1,以致于 P<UI。为了提高电能的利用效率,电力部门采用各种措施 力求提高功率因数。
例9-15 图(a)表示电压源向一个电感性负载供电的电路模 型,试用并联电容的方法来提高负载的功率因数。
解:图(a)电路中的电流为
U 10 0 I S I 2 53 . 1 A 1 Z 3 j4
其波形如下图所示。
图9-24 电阻的瞬时功率和平均功率
瞬时功率p(t)在任何时刻均大于或等于零,电阻始终吸 收功率和消耗能量。此时平均功率的表达式为
U P UI I R R
2
2
(9 20)
p(t ) UI cos UI cos(2t 2 u ) (9 - 18)
下面我们讨论单口网络的几种特殊情况。 1. 单口网络是一个电阻,或其等效阻抗为一个电阻。 此时单口网络电压与电流相位相同,即=u-i=0, cos=1,式(9-18)变为
第九章 正弦稳态电路的分析

1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗(导纳) 分析阻抗(导纳)串、并联电路时,可以利用相关的 并联电路时, 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程,用相量平移求和法则,画出结点 方程, ③ 根据结点上的 方程 用相量平移求和法则, 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知:R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, (瞬时表达式)和各元件的 电路中的电流 瞬时表达式) 试求 电压相量; 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量;(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法: p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法: p UIcosϕ 恒定分量 恒定分量 u i
O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U (2) Z 为一复数,记为 Z = R + jX . I
其中: R — 电阻分量( ); X — 电抗分量()
1 — 容抗 XL = L — 感抗; X C C
U U (3) Z u i I I
Z R X
2
2
= R + jX = |Z| Z
第 九 章
正弦稳态电路的分析
9-1Байду номын сангаас
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 电阻
IR
电感 R
U R I L jL U L
电容
IC
1 j C
1 记为 Y。 即 Y I 。单位:西门子(S). Z U Y I YU I
元件
U
—— 欧姆定律的相量形式
一端口
+ U
I
N0
1 I U Y Z Z U I —— 输入阻抗 (导纳)
N 只含阻抗与受控源
3. 分析
I YU
称阻抗 Z 呈容性;
iii) X = 0 , Z = 0 , u – i = 0 , 电压与电流同相,
称阻抗 Z 呈阻性;
(5) 阻抗三角形
Z R X
2 2
|Z|
|Z|
|X| R
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
IC
j
1 C
U C
IR 1 YR U R R
IL 1 YL U L jL
IC YC jC U
C
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
I I (4) 导纳的性质 Y i u = G + jB = |Y| Y U U
i) B > 0 , Y > 0 , i – u > 0 , 电流超前于电压, 称导纳 Y 呈容性; ii) B < 0 , Y < 0 , i – u < 0 , 电流滞后于电压, 称导纳 Y 呈感性; iii) B = 0 , Y = 0 , i – u = 0 , 电流与电压同相, 称导纳 Y 呈阻性; 思考:感性的阻抗对应的导纳的性质如何?
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
1 记为 Y。 即 Y I 。单位:西门子(S). Z U
电阻
IR
电感
R
U R I L jL U L
电容
U C
U ZR R R IR
U Z L L jL IL
U 1 C ZC j IC C
9-1
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 元件
I
Z
U
Z U I
—— 欧姆定律的相量形式
2. 一端口的阻抗 对于不含独立源的一端口,在正弦稳态下其端口 电压相量与端口电流相量(关联参考方向)之比为 一端口的阻抗,记为 Z。单位:欧姆().
3. 分析
Z U I
(1) 元件与不含独立源的一端口的 VCR 统一表达为: Z U I ,不再表现为微积分的关系;
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
O IL
(6) 阻抗是频率的函数 Z(j) = R() + jX()
X = – Z arctg Z u i R
U Z I
(4) 阻抗的性质
U U Z u i = R + jX = |Z| Z I I
i) X > 0 , Z > 0 , u – i > 0 , 电压超前于电流,
称阻抗 Z 呈感性;
ii) X < 0 , Z < 0 , u – i < 0 , 电压滞后于电流,
(1) 元件与不含独立源的一端口的 VCR 统一表达为: ,不再表现为微积分的关系; I YU I (2) Y 为一复数,记为 Y = G + jB . U 其中: G — 电导分量 (S); B — 电纳分量 (S) 1 — 感纳 BC = C — 容纳; BL L I I I 2 2 (3) Y i u Y G B Y U U U B Y = i – u Y arctg = G + jB = |Y| Y G
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
Y = 0.164 –66 S
仍为感性。
(5) 导纳三角形
|Y|
2
Y G B
2
|Y|
|B| G
(6) 导纳是频率的函数
Y(j) = G() + jB()
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
其中: R — 电阻分量( ); X — 电抗分量()
1 — 容抗 XL = L — 感抗; X C C
U U (3) Z u i I I
Z R X
2
2
= R + jX = |Z| Z
第 九 章
正弦稳态电路的分析
9-1Байду номын сангаас
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 电阻
IR
电感 R
U R I L jL U L
电容
IC
1 j C
1 记为 Y。 即 Y I 。单位:西门子(S). Z U Y I YU I
元件
U
—— 欧姆定律的相量形式
一端口
+ U
I
N0
1 I U Y Z Z U I —— 输入阻抗 (导纳)
N 只含阻抗与受控源
3. 分析
I YU
称阻抗 Z 呈容性;
iii) X = 0 , Z = 0 , u – i = 0 , 电压与电流同相,
称阻抗 Z 呈阻性;
(5) 阻抗三角形
Z R X
2 2
|Z|
|Z|
|X| R
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
IC
j
1 C
U C
IR 1 YR U R R
IL 1 YL U L jL
IC YC jC U
C
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
I I (4) 导纳的性质 Y i u = G + jB = |Y| Y U U
i) B > 0 , Y > 0 , i – u > 0 , 电流超前于电压, 称导纳 Y 呈容性; ii) B < 0 , Y < 0 , i – u < 0 , 电流滞后于电压, 称导纳 Y 呈感性; iii) B = 0 , Y = 0 , i – u = 0 , 电流与电压同相, 称导纳 Y 呈阻性; 思考:感性的阻抗对应的导纳的性质如何?
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
1 记为 Y。 即 Y I 。单位:西门子(S). Z U
电阻
IR
电感
R
U R I L jL U L
电容
U C
U ZR R R IR
U Z L L jL IL
U 1 C ZC j IC C
9-1
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 元件
I
Z
U
Z U I
—— 欧姆定律的相量形式
2. 一端口的阻抗 对于不含独立源的一端口,在正弦稳态下其端口 电压相量与端口电流相量(关联参考方向)之比为 一端口的阻抗,记为 Z。单位:欧姆().
3. 分析
Z U I
(1) 元件与不含独立源的一端口的 VCR 统一表达为: Z U I ,不再表现为微积分的关系;
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
O IL
(6) 阻抗是频率的函数 Z(j) = R() + jX()
X = – Z arctg Z u i R
U Z I
(4) 阻抗的性质
U U Z u i = R + jX = |Z| Z I I
i) X > 0 , Z > 0 , u – i > 0 , 电压超前于电流,
称阻抗 Z 呈感性;
ii) X < 0 , Z < 0 , u – i < 0 , 电压滞后于电流,
(1) 元件与不含独立源的一端口的 VCR 统一表达为: ,不再表现为微积分的关系; I YU I (2) Y 为一复数,记为 Y = G + jB . U 其中: G — 电导分量 (S); B — 电纳分量 (S) 1 — 感纳 BC = C — 容纳; BL L I I I 2 2 (3) Y i u Y G B Y U U U B Y = i – u Y arctg = G + jB = |Y| Y G
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
Y = 0.164 –66 S
仍为感性。
(5) 导纳三角形
|Y|
2
Y G B
2
|Y|
|B| G
(6) 导纳是频率的函数
Y(j) = G() + jB()
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
