向量法求夹角
立体几何中的向量方法求夹角

[策略点睛]
[规范作答] 如图所示,取BC中点 O,连结AO.
因为△ABC是正三角形,所以AO⊥ BC,
因为在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1, 所以AO⊥平面BCC1B1.2分 取B1C1中点为O1,以O为原点, O→B , O→O1 , O→A 为x,y,z轴 的正方向建立空间直角坐标系,则B(1,0,0),D(-1,1,0),A1(0,2, 3),A(0,0, 3),B1(1,2,0).4分
成的角. (2)范围:
(0,
2
]
(3)向量求法:设直线a、b的方向向量为 a, b ,其夹角
为
,则有
cos
|
cos
|
|
|ab| a||b|
(4)注意:两异面直线所成的角可以通过这两条直线的
方向向量的夹角求得,当两方向向量的夹角是钝角时,
应取其补角作为两异面直线所成的角.
例2 Rt ABC中,BCA 900,现将 ABC沿着
3 , 1 , 44
2) 2
DB ( 3 , 3 ,0) z 44
由 C1D m, DB m 得
C1
B1
31 2
C1D m
4
x y 4
2
z 0,
DB m 3 x 3 y 0 44
A1
解得 x 3y 6 z 所以,可取m (3, 3, 6)
30 10
[题后感悟] 如何用坐标法求异面直线所成的 角?
(1)建立适当的空间直角坐标系;
(2)找到两条异面直线的方向向量的坐标形式;
(3)利用向量的夹角公式计算两直线的方向向 量的夹角;
(4)结合异面直线所成角的范围得到异面直线 所成的角.
空间向量直线与平面的夹角公式

直线与平面的夹角公式是什么?
直线与平面的夹角公式为sina=cos=|n·s|/(|n|·|s|),其空间中平面方程为Ax+By+Cz+D=0,法向量n=(A,B,C)。
线面夹角是指过不平行于平面的直线上一点作平面的垂线,这条直线与平面的交点与原直线与平面的交点的连线与原直线构成的锐角或直角。
斜线与它在平面上的射影所成的角为线面夹角。
两平面夹角公式的推导
两平面的夹角公式为:k=(y2-y1)/(×2-x1)。
夹角公式是基本数学公式,分为正切公式和余角公式,正切公式用tan表示,余角公式用cos表示。
两直线的夹角指的是两直线所成的小于等于90°的角,但是当夹角为90°时,k不存在,故当k存在时,正切值始终为正。
空间平面与平面的夹角计算

空间平面与平面的夹角计算在几何学中,空间平面与平面的夹角是指两个平面之间最小的夹角。
计算这个夹角的方法有多种,下面将介绍其中的两种常用方法。
方法一:向量法使用向量法计算空间平面与平面的夹角需要先将两个平面表示为向量形式。
假设有平面P1和平面P2,它们的法向量分别为n1和n2。
则使用以下公式可以计算它们的夹角θ:cosθ = |n1·n2| / (|n1|·|n2|)其中,·表示向量的点乘操作,|n1|表示向量n1的模长。
方法二:法线向量法使用法线向量法计算空间平面与平面的夹角,首先需要求解两个平面的法线向量。
假设两个平面分别为P1和P2,它们的法线向量为n1和n2。
则可以使用以下公式计算夹角θ:cosθ = |n1·n2| / (|n1|·|n2|)其中,·表示向量的点乘操作,|n1|表示向量n1的模长。
需要注意的是,在使用向量法或法线向量法计算夹角时,所得的角度值为弧度制,若需要转换为度数制,可以使用以下公式:角度(度数) = 角度(弧度) × (180 / π)其中,π为圆周率。
以上是两种常用的方法来计算空间平面与平面的夹角。
在实际应用中,根据具体的问题和所需的精度,可以选择合适的方法来计算夹角。
另外,还可以利用数学软件或计算机编程来进行夹角计算。
通过输入平面的相关参数,程序可以自动计算出所需的夹角值,提高计算的效率和准确性。
在工程、建筑设计等领域中,对空间平面与平面的夹角进行准确计算具有重要意义。
合理应用夹角计算方法,可以帮助我们更好地理解和分析空间中的几何关系,为实际问题的解决提供参考和支持。
综上所述,空间平面与平面的夹角可以通过向量法或法线向量法进行计算。
无论是使用哪种方法,都需要将平面表示为向量形式,并根据公式进行计算。
根据具体情况选择合适的计算方法,并且可以借助数学软件或计算机编程来提高计算效率。
夹角的计算在实际应用中具有重要意义,可以帮助我们更好地理解和分析几何关系,为问题的解决提供支持。
3.2.2立体几何中的向量方法(夹角)

P
平面PBC的一个法向量为
1 1 DE (0, , ) 2 2
平面PBD的一个法向量为
1 1 CG ( , , 0) 2 2
A X
D
G B
C
Y
cos DE1 , GC 1 / 2
cos 1/ 2, 60
例3、 如图,在四棱锥P-ABCD中,底面ABCD是 正方形,侧棱PD⊥底面ABCD,PD=DC, 求二面角C-PB-D的大小。
例3 如图,在四棱锥P-ABCD中,底面ABCD是 正方形,侧棱PD⊥底面ABCD,PD=DC, 求二面角C-PB-D的大小。
P
D A
C B
例3 如图,在四棱锥P-ABCD中,底面ABCD是 正方形,侧棱PD⊥底面ABCD,PD=DC, 求二面角C-PB-D的大小。
Z
解 如图所示建立 空间直角坐标系,设DC=1.
F
x
A y
C
B
3 所以B1C1与面AB1C所成的角的正弦值为 。 3
3、 二面角: 设直线 l,m 的方向向量分别为 a , b , 平面 , 的法向量分别为 u, v ,则
(3) , 的夹角为, 则cosθ = cos < u, v >
夹角问题:
u v
P
解2
F
D A
E
C B
练习
的棱长为 1.
求二面角A-BD1 -C的大小.
解1 建立直角坐标系.
z
D1
平面PBD1的一个法向量为
DA1 (0,1,1)
C1
A1
B1
平面CBD1的一个法向量为
向量法求夹角ppt课件
(1)求 cos BE ,DE
(2)记面BC V为a,面DCV为b,∠BED是二面角a—VC —b
的平面角,求∠BED。
z
解:(1)依题意: B(a, a,0),C(-a, a,0),D(-a,-a,0) V
B
设出空间向量的基底,再利用多面体的性质算出或找出其它的 向量。
ppt课件
14
4.法向量的夹角与二面角的平面角的关系
a
n1 g n2
b 设 n1 ,n2 = g
l
设a —l —b的平面
角为
g
-g
a
n1 g n2
两个平面的法向量同时指向或背离。
b
l
ppt课件
15
n1
g
a
n2
设 n1 ,n2 = g
∴ D1B =(2,2,2)
z
A1E =(0,2,1) C1E =(2,0,1)
D
设平面A1EC1的法向量为 n = (x,y,z)A
∴ A1E ·n =2y+ z =0 C1E ·n =2x+ z =0
令 x =1 时,z =-2 ,y =1
∴ n = (1 ,1, -2 )
D1
xA1
C
B E
C1 y
|b|2+|c|2
+2
a
·b
+2 c ·b +2 a ·c
)
O
1 3 3 2
9
3
∴ |OO’| 6 3
c
a
F
cos OO’,BF = OO’ ·BF
两向量夹角计算公式

两向量夹角计算公式好的,以下是为您生成的文章:在咱们学习数学这门神奇又有趣的学科时,两向量夹角计算公式可是个重要的小法宝。
咱们先来说说向量是啥。
向量就像是有方向的箭头,它既有大小又有方向。
想象一下,你在操场上跑步,不仅有跑的速度,还有跑的方向,这速度和方向合起来就是个向量。
那两向量夹角又是啥呢?比如说,有个向量像个勇敢的小箭头往东指,另一个向量像个调皮的小箭头往北指,它们之间形成的那个角度,就是两向量的夹角。
两向量夹角的计算公式是:cosθ = (向量 a·向量 b)/(|向量 a|×|向量 b|)。
这里面的“·”表示向量的点乘,可别小看这个点乘,它的作用可大了。
就拿我之前批改学生作业的事儿来说吧。
有个学生叫小李,他在做关于两向量夹角计算的题目时,那叫一个晕头转向。
我一看他的解题过程,发现他连向量的点乘都给弄错了。
我就给他仔细讲解,“小李啊,你看这两个向量,它们的点乘可不是简单地把对应分量相乘相加就行,还得考虑方向呢。
” 我边说边在纸上画图给他演示,看着他逐渐恍然大悟的表情,我心里那叫一个欣慰。
咱们再深入讲讲这个公式。
分子的向量点乘,就是把两个向量对应分量相乘再相加。
分母呢,是两个向量的模长相乘。
向量的模长就是向量的长度,就像一根箭的长度一样。
在实际应用中,这个公式用处可多啦。
比如在物理学中,计算力的合成和分解时,就经常用到两向量夹角的计算。
还有在工程学中,设计桥梁、建筑的结构时,也得靠它来帮忙。
咱再回到数学题里。
做这类题的时候,一定要仔细分析题目给出的条件,找准向量的坐标或者模长。
有时候一个小马虎,可能就把正负号给弄混了,结果整个答案就错啦。
总之,两向量夹角计算公式虽然看起来有点复杂,但只要咱们多练习、多思考,就一定能把它掌握得牢牢的。
就像咱们走路一样,一开始可能会磕磕绊绊,但走得多了,自然就顺了。
希望同学们在学习的道路上,都能勇敢地面对这些小挑战,把数学这门课学得棒棒的!。
利用向量的数量积和向量积求解向量的模和夹角

利用向量的数量积和向量积求解向量的模和夹角向量是数学中非常重要的概念,它在物理学、几何学和工程学等领域发挥着重要的作用。
利用向量的数量积和向量积,我们可以求解向量的模和夹角,下面将详细介绍这两个概念及其应用。
一、向量的数量积向量的数量积也被称为点积或内积,用符号"·"表示。
给定两个向量a和b,它们的数量积可以通过以下公式计算:a·b = |a| |b| cosθ其中,|a|和|b|分别表示向量a和b的模的大小,θ表示向量a和b之间的夹角。
从公式中可以看出,向量的数量积可以帮助我们求解向量的模和夹角。
二、向量的模向量的模表示向量的长度或大小,并且始终为非负数。
根据向量的数量积公式,我们可以得到以下计算向量模的公式:|a| = √(a·a)这个公式表示,向量a的模等于向量a与自身的数量积的平方根。
通过这个公式,我们可以求解任意向量的模。
三、向量的夹角向量的夹角表示两个向量之间的夹角大小。
根据向量的数量积公式,我们可以得到以下计算夹角的公式:cosθ = (a·b) / (|a| |b|)根据这个公式,我们可以通过求解向量的数量积来计算向量之间的夹角。
进一步地,通过取反余弦函数,我们可以得到夹角的具体数值。
四、向量的向量积另一方面,向量的向量积也被称为叉积或外积,用符号"×"表示。
给定两个向量a和b,它们的向量积可以通过以下公式计算:a×b = |a| |b| sinθ n其中,|a|和|b|分别表示向量a和b的模的大小,θ表示向量a和b之间的夹角,n表示一个垂直于a和b所在平面的单位向量。
从公式中可以看出,向量的向量积可以帮助我们求解向量所在平面的法向量。
五、应用举例下面通过一个例子来演示如何利用向量的数量积和向量积求解向量的模和夹角。
假设有两个向量a = (3, 4)和b = (2, 6),我们要求解它们的模和夹角。
两个向量夹角公式

两个向量夹角公式
两个向量夹角公式是求两个向量夹角的一种方法,也叫做“向量积公式”。
它是向量分析中最基本、最常用的公式之一。
它用于求取两个向量夹角的大小,以及它们之间的关系。
首先,我们来看一下两个向量夹角的定义:两个向量的夹角是指在一个平面上,由这两个向量所构成的三角形的夹角。
两个向量的夹角可以用数字表示,单位是角度。
两个向量夹角公式是:
cosθ = a · b/|a||b| (1)
其中,a和b分别代表两个不同的向量,θ代表两个向量之间的夹角,“·”代表向量的点积,|a|和|b|代表a 和b向量的模长。
要根据两个向量夹角公式计算出两个向量之间的夹角,首先要计算点积,即a·b,然后将点积除以向量a和b的模长的乘积,最后将得出的结果带入cosθ的公式中,就可以求出两个向量的夹角了。
两个向量夹角公式的一个重要特点是,它不仅适用于两个向量,而且可以用于任意的n个向量,只要它们之间的夹角是相同的,就可以求出这n个向量之间的夹角了。
此外,两个向量夹角公式可以用来识别两个向量之间的关系。
因为夹角的大小可以反映出两个向量之间的关系,当两个向量之间的夹角是0°时,说明它们是平行的;当两个向量之间的夹角是90°时,说明它们是垂直的;当两个向量之间的夹角是180°时,说明它们是相反的。
总之,两个向量夹角公式是一种简单有效的方法,它可以用来计算两个向量之间的夹角和关系,使数学家们能够快速准确的求出所需的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
θ= g1 2
当 n 与向量 BA 的夹角为钝角g
2
A
g2
n
θ
β B
θ= g 2 2
C
例1 如图所示,已知正四面体O—ABC, E、F分别是AB、OC的中点。 (1) 求OE与BF所成的角; (2)求BF与平面ABC所成的角。 分析:(1)设 OA = a
OB = b
O
OC = c a b
F E D B C
B
)
(2002年全国高考)
F1 A1 B1 C1 E1
D1
DE1 3 = FE1 又 DF 3 ∴ △FDE1为等边三角形 ∴∠ FE1D= 60°
A
解法2:建立如图所示的直角坐标系。
3 3 , C1 1, 3, 2 , D 0, 3,0 , B , , 0 2 2 1 3 . E1 , , 2 2 2 A1 1 3 1 3 ,DE , , 2 BC1 , 2 . 2 2 1 , 2 2 3 BC1 · DE1 1 , ∴cos BC1 DE1= 2 |BC1| |DE1| 3 2 A
C1
C (0,1,0), A1(1,0,1), B (1,1,0),
D (0,0,0), C1(0,1,1),
F
D A E B
C
y
A1C = (-1,1, -1), C1D = (0, -1, -1),
BD =(-1, -1, 0)
A1C⊥平面BDC1
x
A1C · C1D = 0-1+1 =0 A1C ⊥ C1D A1C · BD = 1-1+0 =0 A1C ⊥ BD C1D∩ BD=D
-g
两个平面的法向量同时指向或背离。
n1
a
l
g n 2
b
n1
g
a
l
n2
b
设 n1 , n2 = g
设a —l —b的平面 角为
g
g
两个平面的法向量一个指向另一个背离。
a
n1
l
n2
b
例1 如图,在棱长为1的正方体ABCD—A1B1C1D1 中,AC与BD交于点E, C1B与CB1交于点F. z (1) 求证:A1C⊥平面BDC1 D1 (2) 求二面角B—EF—C的大小 (结果用反三角函数表示) B 1 A 1 证明:(1)以点D为坐标原点建立 如图所示的空间直角坐标系,则
A1E =(0,2,1)
设平面A1EC1的法向量为 n = (x,y,z) A ∴
A1E ·n =2y+ z =0
C1E ·n =2x+ z =0
y =1 令 x =1 时,z =-2 ,
∴ n = (1 ,1, -2 ) ∴ D1B ·n = 0 D1B ⊥ n D1B 平面A1EC1
x
A 1
OB = b
O
c a b
C E F
B
1 2
1 OE ·BF 2 cos OE ,BF = | OE | | BF | 3 3 2 2 2 3
∴OE与BF所成的角为
O
c a b
A E C F
2 arccos 2 3
B
(2)求BF与平面ABC所成的角。 (2)作OO’⊥平面ABC于点O’,设OO’与BF所成
OA = a
OC = c 1 c |a |= |b |= |c |= 1 则a· b =c · b =a · 2 1 1 a ( + ) OE b c -b BF 2 2 1 1 · OE · BF = ( a + b ) ( c - b ) 2 2 A 2 1 1 1 c + b· c -a · b-|b | ) ( a· 2 2 2 11 1 1 1 24 4 2
C
2 1 1 1 2 2 a c b c c a b b b c 3 2 2 2 2 1 1 1 1 1 1 3 4 4 2 2 2
a
cos OO’,BF
O
c
F
2 2 ∴求BF与平面ABC所成的角 arccos arcsin 2 3 3
1 cos A1C , D1B = | A1C |· | D1B | 3
A1C · D1B
A x
例2.(2001年全国)如图,在底面是直角梯形的四 棱锥S—ABCD中, ∠ABC=90°,SA⊥面ABCD, 1 SA= BC=AB=1, AD . 求面SCD 2 与面SBA所成的二面角的正切值。 解法1:延长BA、CD相交于E, 连接SE,则SE是所求二面角的棱 AD ∥BC EA=AB=SA BC=2 AD SE⊥SB SA⊥面ABCD SA⊥BC BC ⊥AB BC ⊥ 面SEB ∴SB是SC在面SEB上的射影。
故 BC1 , DE1 = 60° ∴ E1D与BC1所成的角是60° 故应选 B
x
z F1 E1
D1
B1 C1
F
E D
B
C
y
一 法向量: 如果一个向量所在直线垂直于平面,则 该向量是平面的一个法向量。 二 法向量的主要作用 1 证明线面平行 取和直线平行的向量,验证该向量和法向量的点积是否为零。 设平面β的法向量为 n , a 是 a 的方向向量.
2 3
2 arccos 3
b
A C
E
O' B
评析:利用向量讨论线面关系不需作辅助线,但需要正确 设出空间向量的基底,再利用多面体的性质算出或找出其它的 向量。
4.法向量的夹角与二面角的平面角的关系
n1
a
l
g n 2
b
g
设 n1 , n2 = g
设a —l —b的平面 角为
2 2 2 2 2 3a 2 h 2 ∴ BE · DE 2 4 2 2 2 3a a h 1 2 2 又|BE| 10 a h 2 2 2 2
3a a h 1 10a 2 h 2 |DE| 2 2 2 2
设平面SCD的法向量 n =(x,y,z) 1 , 1 , 0 DC 2 1 SD ,0,1 A 2 1 n· DC =0 x y 0 即 2 1 n· SD =0 xz 0 2
y
B
C
D
x
1 1 令x=1,则 y , z 2 2 1 1 ∴ n 1, , 2 2 6 AD ∴cosa= n · |n|· 3 |AD|
2 2 2
a a h E , , 2 2 2 3a a h a 3a h ∴ BE , , DE , , 2 2 2 2 2 2
A x D
E
C
O
B
y
3a a h a 3a h ∴ BE , , DE , , 2
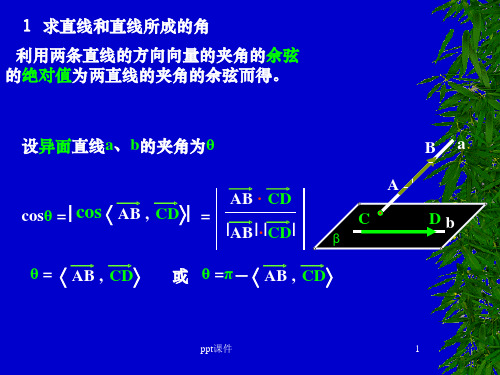
1 求直线和直线所成的角 利用两条直线的方向向量的夹角的余弦 的绝对值为两直线的夹角的余弦而得。
设异面直线a、b的夹角为θ AB ·CD A C
β
B
a
cosθ = | cos AB , CD| = θ=
|AB | · |CD|
Db
AB , CD
或 θ =π- AB , CD
[例1] 正六棱柱ABCDEF—A1B1C1D1E1F1 的底面边长为1,侧棱长为 2 ,则这个 棱柱的侧面对角线 E1D与BC1所成的角是( A.90° B. 60° C. 45° D. 30° 解法一: 连结FE1、FD 、BC1 ∴四边形BFE1C1是平行四边形 ∴ FE1∥ BC1 ∴∠ FE1D是异面直线E1D与BC1所成的角或补角 ∵底长为1,棱长为 2
A1
D1
E
C1 O
B1
BD1∥平面A1C1 E
证法二:如图所示建立直角坐标系,且设 正方体的棱长为2, D1(0,0,0), B(2,2,2), A1(2,0,0), C1(0,2,0), E(2,2,1) ∴ D1B =(2,2,2)
z
C1E =(2,0,1)
D B D1 E C1 y B 1 C
A E O' C F
求出 OE ,BF, 然后可求 cos OE
| OE | | BF |
BF所成的角为θ 0 ,则BF与平面ABC所成的角为 2
(2)可过点O作OO’⊥平面ABC于点O’, 若OO’与
B
2
解:(1)设正四面体O—ABC的棱长为1,
解: (2)同(1)可知, D1B⊥平面AB1C 由(1) A1C⊥平面BDC1
z C1
即向量 D1B 是平面AB1C的一个法向量。, D1
A1C 是平面BDC1的一个法向量。
∵ A1C = (-1,1, -1),
A1
B1 F
D y C E B
D1B = (1,1, -1),
1 故二面角B—EF—C的为 arccos 3
O
c
F
b
C O' B
2 1 | OO’| ( a +b + c ) 9 1 2 2 2 ( + |a| |b| +|c| +2 a · b +2 c ·b +2 a · c ) O 9 c 1 2 6 3 3 ∴ | OO’| F 9 3 a 3 OO’ · BF b cos OO’,BF = A | OO’| | BF | O' 1 1 E ( a + b + c )· ( c -b ) B 3 2 = 6 3 3 2 2 1 1 1 2 2 a c b c c a b b b c 3 2 2 2 2
