频率特性分析的bode图法
合集下载
自动控制原理3第三节典型环节的频率特性

左图是不同阻尼系数情况下的 对数幅频特性和对数相频特性 图。上图是不同阻尼系数情况 下的对数幅频特性实际曲线与 渐近线之间的误差曲线。
1 2T 1 T 2 T 5 T 10 T
1 5T
Saturday, November 05, 2016
15
微分环节的频率特性
⒌ 微分环节的频率特性: 微分环节有三种:纯微分、一阶微分和二阶微分。传递函 数分别为: G( s) s
05, 2016
12
振荡环节的波德图
2 T ( ) tg 相频特性: 1 T 2 2
1
几个特征点: 0, ( ) 0;
1 , ( ) ; , ( ) 。 T 2
由图可见:
K 10, T 1, 0.3 10 G ( j ) 2 s 0.6s 1 1 o T
1
幅频特性为: 相频特性为:
A( )
(1 T 2 2 )2 (2T )2 2 T ( ) tg 1 1 T 2 2
L( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2 对数幅频特性为:
低频段渐近线: T 1时,L( ) 0 高频段渐近线: T 1时, L( ) 20 log (T 2 2 ) 2 40 log T 1 两渐进线的交点 o 称为转折频率。斜率为-40dB/Dec。 T Saturday, November
1 2
T
时,无谐振峰值。当
M p A( p )
1 2
1 0.707时, p 0 。 2
时,有谐振峰值。
1 2 1 2
1 当 0 , A(0 ) , 。 L ( ) 20 lg 2 0 2
第六章-2-Bode图

Wintersweet 浙江大学控制科学与工程学系
2
Bode plots (Logarithmic plots )
Bode图(对数坐标图)
对数坐标图的优点 1) 将乘积和除法的数学操作转化为加法和减法; 2) 传递函数的获取大多采用图表法,而不是分析法; 3) 半对数坐标扩展了低频段 首先运用直线近似的方法来获得系统的近似特性,然后修正直线, 提高精度. 对数坐标图 足够多的数据 极坐标图
dB
可以计算出 ω 对应的Lm,然后绘制出频率响应。但是绘制对数幅 频渐近特性曲线会更容易,也更常用. 当 ω很小时, 也就是说 ωT<<1
Lm1 jT 20 log1 0
1
dB
Lm(dB) 20 -20 1/T 10/T ω
对数幅频渐近特性曲线 Lm 在低 频段为 0 dB 线
1
浙江大学控制科学与工程学系
Bode plots (Logarithmic plots )
自动控制理论
第六章
频域特性分析法
周立芳
浙江大学控制科学与工程学系
浙江大学控制科学与工程学系
Bode plots (Logarithmic plots )
主要内容
简介 Bode 图 (对数频率特性曲线) 极坐标图 Nyquist’s yq 稳定判据 相角裕度和幅值裕度,以及与稳定性的关系 ………
dB
K m (1 jT1 )(1 jT2 ) r G ( j ) 2 ( j ) m (1 jTa )[1 (2 / n ) j (1 / n )( j ) 2 ]
对数幅值:
LmG ( j ) LmK m Lm(1 jT1 ) rLm(1 jT2 ) mLm( j ) 2 1 2 Lm L (1 jTa ) Lm L 1 j 2 ( j ) n n
系统的频率特性分析(第二讲)

-45°
-90° 111
20T 10T 5T
112 2T T T
5 10 20 TTT
一阶惯性环节伯德图
一阶微分环节的Bode图与惯性环节的Bode图关于 横轴对称。
二阶微分环节的频率特性
③ 二阶微分环节: G(s) 2s2 2 s 1
幅频和相频特性为:
A
(1 22 )2 (2 )2 ,() arctan 2 1 22
常数T变化时,对数幅频特性和对数相频特性的形状都不变,
仅仅是根据转折频率1/T的大小整条曲线向左或向右平移即可。
而当增益改变时,相频特性不变,幅频特性上下平移。
G(s) 5 s 1
当增益 改变时, 相频特 性不变, 幅频特 性上下 平移。
Matlab 绘制的惯性环节的Bode图
4
振荡环节(要重视)G(s)
0.7 0.8 1.0
5
10
T
T
-30°
-60°
0.1
-90° 0.2
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
左图是不同阻尼系数情况下 的对数幅频特性和对数相频 特性图。上图是不同阻尼系 数情况下的对数幅频特性实 5 10 际曲线与渐近线之间的误差 T T 曲线。
1
0.086 0.34 1.29 2.76 4.30 6.20 4.30 2.76 1.29 0.34 0.086
K 10,T 1, 0.3
G(
j )
s2
10 0.6s
1
o
1 T
40dB/ Dec
第6章 频率特性 3 bode plot

Automatic control
Lecture: Bode Plot
L (w ) = -20 lg 1 + T 2 w 2
工程上常采用近似画法来画幅频曲线,即利用渐进线 近似表示,其原理如下:
当T w << 1时,即w << 1/T ,则
-20 lg wT
L (w ) = -20 lg 1 + T 2 w 2 » -20 lg1 = 0 幅频曲线是一条零分贝水平线。
3
2012/11/6
Automatic control
Lecture: Bode Plot
Automatic control
Lecture: Bode Plot
G ( s ) = Ts + 1 频率特性 G ( jw ) = 1 + jT w
(4). 一阶微分环节
L (w ) = 20 lg 1 + jT w = 20 lg 1 + T 2 w 2 j (w ) = (1 + jT w )
2
2
当w << wn时, L (w ) = -20 lg1 = 0 ,渐近线为一条 0dB线。
当w >> wn时, w2 w = -40 lg , 渐近线为 2 wn wn 一条过 (w, n 0) 点﹑斜率为 - 40dB/dec的直线。 L (w ) » -20 lg
éæ w 2 ö æw÷ öù ç1- ÷ ç ÷ú ÷ + j 2x ç j (w ) = - êêç ÷ 2÷ ç ç ø è wn ÷ øúúû êëè wn ÷
Automatic control
Lecture: Bode Plot
第4章第12节频率响应与频率特性及频率特性的图示法

4.1频率响应与频率特性
▪ 频率特性是复变量s=jω的复变函数,因此 有
▪ 一般地,系统对正弦输入信号的稳态响应 为
4.2频率特性的图示法——奈氏图 和伯德图
4.2.1奈魁斯特图
▪ 奈魁斯特(Nyquist)图也称极坐标图。在 数学上,频率特性可以用直角坐标式表 示,;也可以用幅相式(指数式)表示, 即
因是系统有储能元件、有惯性,对频率 高的输入信号,系统来不及响应。 (3)系统的频率特性是系统的固有特性,取 决于系统结构和参数。
4.1频率响应与频率特性
4.1.6求取频率特性的解析方法 ▪ 当已知系统的传递函数时,可按下式求取,
即
G(j)G(s) sj
▪ 当从系统原理图开始求取系统的频率特性 时,应该先求出系统的传递函数。
4.1频率响应与频率特性
可以看出: 随着输入信号频率的变化,输出、输入信号 的幅值比和相位差将会相应地随频率而发生 变化。 因此,可以利用这一特性,保持输入信号的 幅值不变,不断改变输入信号的频率,研究 系统响应信号的幅值和相位随频率的变化规 律,即可达到研究系统性能的目的。
4.1频率响应与频率特性来自4.1频率响应与频率特性
4.1.3频率响应
▪ 稳定的线性系统对正弦输入的稳态响应称 为频率响应。
▪ 另外一种表达: 当正弦信号作用于稳定的线性系统时,系 统输出响应的稳态分量是与输入同频率的 正弦信号,这种过程称为系统的频率响应。
线性系统的频率响应
求上图中输出信号与输入信号的 1、相位差A(ω) 2、幅值比ψ(ω)
两个问题:
1、正弦输入信号可不可以代表所 有信号?
2、什么是系统的频率特性?其图 形表示是什么样子?
4.1频率响应与频率特性
04 频率特性法——奈氏判据和伯德图判据

分析开环系统 G(s)H(s)的零点 都在S左半平面
一、开环频率特性与闭环频率 特性的关系
开环频率特性
G(s)H(s)
闭环频率特性
G( s ) ( s) 1 G( s ) H ( s )
F(s)=1+G(s)H(s)
二、奈斯判据
奈斯判据: s沿着奈氏路径绕一圈(当ω从 -∞→+∞变化时),G(jω)H(jω)曲线逆 时针包围(-1,j0)点R圈。 若 R=P (右半平面极点个数即正 实部极点分析系统稳定性。
Im
P0
0
Im
P 1
0
0
R
Re
R
K
0
Re
(a)
(b)
解: (a) N= N+ - N –=(0-1)= -1,P =0,故
Z=P-2N=2,闭环系统不稳定。 (b) K>1时,N= N+ - N - =1-1/2= 1/2,P=1,故 Z= P-2N=0,闭环系统稳定; K<1时, N = N+ - N - =0-1/2= -1/2,且已知P =1,故 Z= P-2N=2,闭环系统不稳定; K=1时,奈氏曲线穿过 (-1,j0) 点两次,说明有两个 根在虚轴上,闭环系统不稳定。
R=2N=2(N+-N-)=P
注意:
正穿越对应于Bode图φ(ω)曲线当ω增大 时从下向上穿越-180°线; 负穿越对应于Bode图φ(ω)曲线当ω增大 时,从上向下穿越-180°线。
例:开环特征方程有两个右根,P=2,试判定闭环系统的稳定性。 解:
P=2
正负穿越数之差(N+-N-)为1
第5章4——Bode图
2
1 2 n
2
n
2 arc tg n 2 1 2 n
0 0 ( ) 90 n 180
autocumt@ 22
振荡环节L()
L()dB 40 20 0dB -20
(rad / s)
10 -2
10 -1
1
10
0
2 3 4
10
1
autocumt@
自动控制原理
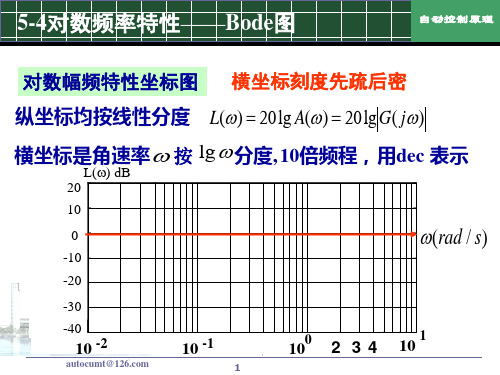
对数分度:
lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
lg 7 0.845 lg 8 3 lg 2 0.903 lg 9 2 lg 3 0.954
()º
(rad / s)
10 -2
autocumt@
10 -1
3
100
10
1
20 10 0
自动控制原理
L() dB -10
-20 -30 -40 900 450
( )
00 0 -450 -900
-1350
完 整 图 二 合 一
-1800
10 -2
autocumt@
[-20] 0.1 0.2
1
2
10 20
[-20]
100
16
5-4 对数频率特性——Bode图
(5)一次微分环节
传递函数: G(S) TS+ 1 频率特性: G ( j ) Tj 1
0 0 1 相频特性 ( ) arctanT 45 T 90
自动控制原理:第六章频域分析法——伯特图及稳定性分析

• 当阻尼系数接近1时,振荡环节具有低通滤波的作用; • 而随着减小,=n=1/T处的幅值迅速增大,表明其对输
入信号中该频率附近分量的放大作用逐渐加强,此时,振
荡环节具有选频作用。
6.4 系统开环频率特性-典型环节的伯德图
40
Bode Diagram
二阶微分环节:
30
20
转折频率 渐近线
L() /(dB)
10 /T
1) 将乘除运算转化为加减运算,因而可通过简单的图像叠加 快速绘制高阶系统的伯德图 ;如 G( j) A1()e j1() A2 ()e , j2 () 则20lgA1()A2()=20lgA1()+20lgA2()
2) 伯德图还可通过实验方法绘制,经分段直线近似整理后, 很容易得到实验对象的频率特性表达式或传递函数.
i 1
i m1 1
v n1
v n1 nv n1 2
( jTl 1)
(1 Tl2 2 2 j lTl )
l v 1
l v n1 1
(6 - 17)
其 中 ,K ,0 i 1,0 l 1, i 0,Tl 0都 为 常 数 。
除此外,也存在某个Tl<0,开环不稳定,但闭环可能仍然 稳定的情况。
1
A(ω)
1 ωT 2 2 2ζωT 2
L() /(dB)
10
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40
180
转折频率 渐近线
135
(ω)
arctan
1
2ζωT
ωT
2
90 45
0
() /()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
◆Bode图的优点
① 可将串连环节幅值的乘除化为加减,系统的Bode图为各环节的Bode图 的线性叠加;
② 可通过近似方法作图;先分段用直线作出对数幅频的渐近线,再用修 正曲线对渐近线进行修正。
③ 可分别作出各环节的Bode图,然后用叠加法得出系统的Bode图。 ④ 横坐标采用对数分度,所以能把较宽频率范围的图形紧凑地表示出来。
2022/3/23
11
对数幅频特性
ωT : 转角频率
20lg G( j) 20lg T 20lg T2 2
低频段(ω<<ωT), 20lgG(j)20lgT-20lgT=0dB 高频段(ω>>ωT), 20lgG(j)20lgT-20lg 始于点(ωT ,0), 斜率-20dB/dec的直线 对数相频特性:
应重点掌握)。 将函数化成实部和虚部之和或差,再用欧拉公式。
G( j) G(s) | G( j) | ejG( j) s j
3.用实验的方法求取。
2022/3/23
3
例 系统的传递函数为 G(s) K ,
Ts 1
若输入信号为 xi(t)=xisint,求系统的频率特性
和频率响应。
第一,用j替换s,即G( j) G(s) s j
对数相频特性:过点(0,90o )平行于横轴的直线
2022/3/23
10
(4)惯性环节
惯性环节的频率特性为G( j) 1 1 jT
若令T
1 T
,设T
为转角频率
则有G( j) T T j
故幅频特性为G( j) T T2 2
相频特性为G( j) arctan T
对数幅频特性 20lg G( j) 20lg T 20lg T2 2
20lg G( j) 20lg T 20lg T2 2
低频段渐近线: 20lgG(j)0dB
误差:e() 20lg T 20lg T2 2
高频段渐近线: 20lgG(j)20lgT-20lg e() 20lg 20lg T2 2
最大误差发生在转角频
率 T 处,其误差为 -3dB。
1 T 2 2
2022/3/23
5
◆频率特性的对数坐标图(Bode图)
对数坐标图由对数幅频特性图和对数相频特性图组成
分别表示幅频特性和相频特性
① 对数幅频特性图
横坐标:ω,对数分度,标注真值; 纵坐标:G(j)的分贝值dB, 1dB=20lgG(j);线性分度。
0dB,| G( j) | A() X 0 () 1
Xi 输出幅值等于输入幅值
dec (10倍频程)
dB 0,| G( j) | A() X 0 () 1
Xi 输出幅值 输入幅值(放大)
dB 0,| G( j) | A() X 0 () 1
Xi 输出幅值 输入幅值(衰减)
2022/3/23
② 对数相频特性图 横坐标:同上 纵坐标:∠G(j) ,线性分度
第二,利用复变函数的欧拉公式,得到系统的频率特性
G( j) G(s)
K
K
earctanT
s j 1 jT 1 T 2 2
2022/3/23
即
A()
G(
j)
K
1 T 2 2
() G( j) arctanT
G( j) G(s) K s j 1 jT
(1
K(1 jTw) jT)(1 jTw)
20lgG(j)= 20lg 1/= - 20lg
对数幅频特性:过点(1,0)斜率-20dB/dec的直线 对数相频特性:过点(0,-90o )平行于横轴的直线
2022/3/23
9
(3)微分环节
传递函数 G(s)=s 频率特性G(j)=j 20lgG(j)= 20lg G(j)= 90o
对数幅频特性:过点(1,0)斜率20dB/dec的直线
相频特性
放大电路的电压放大倍数与频率的关系称为幅频特性, 输出信号与输入信号的相位差与频率之间的关系称为相频特性。 两者统称频率特性。
◆频率特性:当输入量波形变化时,其输出量随频率变化的特性。
2022/3/23
2
◆频率特性的三种求法
1.根据系统的频率响应来求取。
2.将传递函数中的s换为jω (s= jω )来求取(最常用,
行拉氏变换 • w=logspace(-2,3,100); %产生介于10^(-2)和10^3之间的100个频率点 • grid; • bode(nunG1,denG1,w) %绘制bode图。
(exno2)
2022/3/23
14
• 谢谢!
2022/3/23
15
K(1 jTw) 1 T 2 2
1
K T 2
2(实部)
j
1
KTw T 2
2(虚部),
利用欧拉公式得到
K(2 1 T 2 2) (1 T 2 2)2 e
arcta
nT
K
e a r c ta nT
1 T 2 2
4
第三,系统的频率响应
xo(t) Xi G( j) sin[t G( j)] XiK sin(t arctanT)
2022/3/23
(matlab:GXhuanjie)
G(jω) arctan ω ωT
=0, G(j)=0°;
=T,G(j)=-45°; =, G(j)=-90°;
对数相频特性曲线对称于点(T,-45°) ≤0.1T 时,G(j) 0° ≥10T 时,G(j)90°
12
误差修正曲线
对数幅频特性
在分析和研究系统时,低频特性很重要。
2022/3/23
7
◆典型环节的Bode图
(1)比例环节
比例环节的频率特性为 G(j)=K
其对数幅频特性和相频特性分别为 20lgG(j)=20lgK G(j)=0。
2022/3/23
8
(2)积分环节
积分环节的传递函数为G(s)=1/s,则频率特性为G(j)=1/j, 故幅频特性|G(j)|=1/,相频特性G(j)= -90。
频率特性分析的Bode图法
李焱
2022/3/23
1
◆频率响应
线性定常系统对谐波输入的稳态响应。瞬态分量:XiKTw 1T2w2
t
*eT
系统的稳态响应公式
xo(t) G( j) Xi sin[t G( j)]
则系统的幅频特性和相频特性分别为
A()
Xo()
G( j) 幅频特性
X22/3/23
13
作传递函数的为 G(s) (5s2(42)0.2(5s0.005.s5) 2)的系统的BODE图
• k=24;nunG1=k*[0.25 0.5]; %系统的传递函数,分子及分母 • denG1=conv([5,2],[0.05 2]);%conv 用来求卷积的函数命令,在此处是进
◆Bode图的优点
① 可将串连环节幅值的乘除化为加减,系统的Bode图为各环节的Bode图 的线性叠加;
② 可通过近似方法作图;先分段用直线作出对数幅频的渐近线,再用修 正曲线对渐近线进行修正。
③ 可分别作出各环节的Bode图,然后用叠加法得出系统的Bode图。 ④ 横坐标采用对数分度,所以能把较宽频率范围的图形紧凑地表示出来。
2022/3/23
11
对数幅频特性
ωT : 转角频率
20lg G( j) 20lg T 20lg T2 2
低频段(ω<<ωT), 20lgG(j)20lgT-20lgT=0dB 高频段(ω>>ωT), 20lgG(j)20lgT-20lg 始于点(ωT ,0), 斜率-20dB/dec的直线 对数相频特性:
应重点掌握)。 将函数化成实部和虚部之和或差,再用欧拉公式。
G( j) G(s) | G( j) | ejG( j) s j
3.用实验的方法求取。
2022/3/23
3
例 系统的传递函数为 G(s) K ,
Ts 1
若输入信号为 xi(t)=xisint,求系统的频率特性
和频率响应。
第一,用j替换s,即G( j) G(s) s j
对数相频特性:过点(0,90o )平行于横轴的直线
2022/3/23
10
(4)惯性环节
惯性环节的频率特性为G( j) 1 1 jT
若令T
1 T
,设T
为转角频率
则有G( j) T T j
故幅频特性为G( j) T T2 2
相频特性为G( j) arctan T
对数幅频特性 20lg G( j) 20lg T 20lg T2 2
20lg G( j) 20lg T 20lg T2 2
低频段渐近线: 20lgG(j)0dB
误差:e() 20lg T 20lg T2 2
高频段渐近线: 20lgG(j)20lgT-20lg e() 20lg 20lg T2 2
最大误差发生在转角频
率 T 处,其误差为 -3dB。
1 T 2 2
2022/3/23
5
◆频率特性的对数坐标图(Bode图)
对数坐标图由对数幅频特性图和对数相频特性图组成
分别表示幅频特性和相频特性
① 对数幅频特性图
横坐标:ω,对数分度,标注真值; 纵坐标:G(j)的分贝值dB, 1dB=20lgG(j);线性分度。
0dB,| G( j) | A() X 0 () 1
Xi 输出幅值等于输入幅值
dec (10倍频程)
dB 0,| G( j) | A() X 0 () 1
Xi 输出幅值 输入幅值(放大)
dB 0,| G( j) | A() X 0 () 1
Xi 输出幅值 输入幅值(衰减)
2022/3/23
② 对数相频特性图 横坐标:同上 纵坐标:∠G(j) ,线性分度
第二,利用复变函数的欧拉公式,得到系统的频率特性
G( j) G(s)
K
K
earctanT
s j 1 jT 1 T 2 2
2022/3/23
即
A()
G(
j)
K
1 T 2 2
() G( j) arctanT
G( j) G(s) K s j 1 jT
(1
K(1 jTw) jT)(1 jTw)
20lgG(j)= 20lg 1/= - 20lg
对数幅频特性:过点(1,0)斜率-20dB/dec的直线 对数相频特性:过点(0,-90o )平行于横轴的直线
2022/3/23
9
(3)微分环节
传递函数 G(s)=s 频率特性G(j)=j 20lgG(j)= 20lg G(j)= 90o
对数幅频特性:过点(1,0)斜率20dB/dec的直线
相频特性
放大电路的电压放大倍数与频率的关系称为幅频特性, 输出信号与输入信号的相位差与频率之间的关系称为相频特性。 两者统称频率特性。
◆频率特性:当输入量波形变化时,其输出量随频率变化的特性。
2022/3/23
2
◆频率特性的三种求法
1.根据系统的频率响应来求取。
2.将传递函数中的s换为jω (s= jω )来求取(最常用,
行拉氏变换 • w=logspace(-2,3,100); %产生介于10^(-2)和10^3之间的100个频率点 • grid; • bode(nunG1,denG1,w) %绘制bode图。
(exno2)
2022/3/23
14
• 谢谢!
2022/3/23
15
K(1 jTw) 1 T 2 2
1
K T 2
2(实部)
j
1
KTw T 2
2(虚部),
利用欧拉公式得到
K(2 1 T 2 2) (1 T 2 2)2 e
arcta
nT
K
e a r c ta nT
1 T 2 2
4
第三,系统的频率响应
xo(t) Xi G( j) sin[t G( j)] XiK sin(t arctanT)
2022/3/23
(matlab:GXhuanjie)
G(jω) arctan ω ωT
=0, G(j)=0°;
=T,G(j)=-45°; =, G(j)=-90°;
对数相频特性曲线对称于点(T,-45°) ≤0.1T 时,G(j) 0° ≥10T 时,G(j)90°
12
误差修正曲线
对数幅频特性
在分析和研究系统时,低频特性很重要。
2022/3/23
7
◆典型环节的Bode图
(1)比例环节
比例环节的频率特性为 G(j)=K
其对数幅频特性和相频特性分别为 20lgG(j)=20lgK G(j)=0。
2022/3/23
8
(2)积分环节
积分环节的传递函数为G(s)=1/s,则频率特性为G(j)=1/j, 故幅频特性|G(j)|=1/,相频特性G(j)= -90。
频率特性分析的Bode图法
李焱
2022/3/23
1
◆频率响应
线性定常系统对谐波输入的稳态响应。瞬态分量:XiKTw 1T2w2
t
*eT
系统的稳态响应公式
xo(t) G( j) Xi sin[t G( j)]
则系统的幅频特性和相频特性分别为
A()
Xo()
G( j) 幅频特性
X22/3/23
13
作传递函数的为 G(s) (5s2(42)0.2(5s0.005.s5) 2)的系统的BODE图
• k=24;nunG1=k*[0.25 0.5]; %系统的传递函数,分子及分母 • denG1=conv([5,2],[0.05 2]);%conv 用来求卷积的函数命令,在此处是进
