圆的面积和阴影面积计算
初中几何圆、扇形、弓形的面积及阴影部分面积专项

初中几何圆、扇形、弓形的面积及阴影部分面积专项一、圆的面积计算公式:S=R 2,圆心角是1°的扇形面积等于圆面积的1360,圆心角是n 度的扇形面积等于圆的面积的360n ,扇形的弧长等于l=180n R ,⇒S 扇=12lR 。
二、运用公式法、割补法、拼凑法、等积变化法、平移法、旋转法、构造方程法等方法求组合图形的面积。
三、运用割补法、平移法、旋转法、等积变换法、容斥原理求阴影部分面积。
1、弓形面积弓形的面积可以转化为扇形的面积与三角形的面积之差,如下图所示,弓形AmB 的面积S弓形=S 扇性AOB -S △AOB弓形的面积可以转化为:扇形的面积与三角形的面积之和,如下图所示弓形AmB 的面积S 弓形= S 扇性AOB +S △AOB注:①当弓形所含的弧是劣弧时如甲图所示,弓形AmB 的面积S 弓形=S 扇性AOB -S △AOB②当弓形所含的弧是优弧时,如图乙所示,AnB 的面积S 弓形= S 扇性AOB +S △AOB③当弓形所含的弧是半圆时,弓形的面积S 弓形=12S 圆 如图:半径OA=6cm,C 为OB 的中点,∠AOB=120°,求阴影部分面积S 。
(右:乙图)解:由图形可知,S 阴影ABC =S 扇性ABO -S △ACO ,而S 扇形ABO =21206360⋅=12,S △ACO =12×6×3×sin60°=932,所以S 阴影ABC =(93122-)cm 2。
2、割补法凡求与圆有关的不规则图形面积问题,一般都要把它转化为三角形、扇形、弓形的面积来求解,在进行复杂的图形的面积计算时,时常通过添加辅助线,把图形分割成若干个基本图形求解,这种求解的方法是经常用到的。
如图:⊙O 中的弦AC=2cm ,圆周角∠ABC=45°,求图中阴影部分的面积。
(部分与整体)解:做⊙O 的直径AB 1,则连结OC 、B 1C ,∠ACB=90°,∠B=∠B 1,AB 1=22,∵OA=2,∴S △AOC=1,S 扇形AOC =12,∴S 阴影=S 扇形AOC -S △AOC =12-1 例二:如图在两个半圆中大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN=a ,ON ,CD 分别为两圆的半径,求阴影部分的面积。
小学六年级数学上册(人教版)——圆与求阴影部分面积

小学六年级数学上册(人教版)——圆与求阴影部分面积编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(小学六年级数学上册(人教版)——圆与求阴影部分面积)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为小学六年级数学上册(人教版)——圆与求阴影部分面积的全部内容。
小学六年级数学上册(人教版) ——圆与求阴影部分面积例1。
求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积.(单位:厘米)例3。
求图中阴影部分的面积.(单位:厘米)例4。
求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7。
求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)小学六年级数学上册(人教版)——圆与求阴影部分面积例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积.(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12。
求阴影部分的面积。
(单位:厘米)例13。
求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15。
已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16。
求阴影部分的面积.(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18。
如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长.例19。
正方形边长为2厘米,求阴影部分的面积.例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21。
圆-阴影部分面积(附答案)
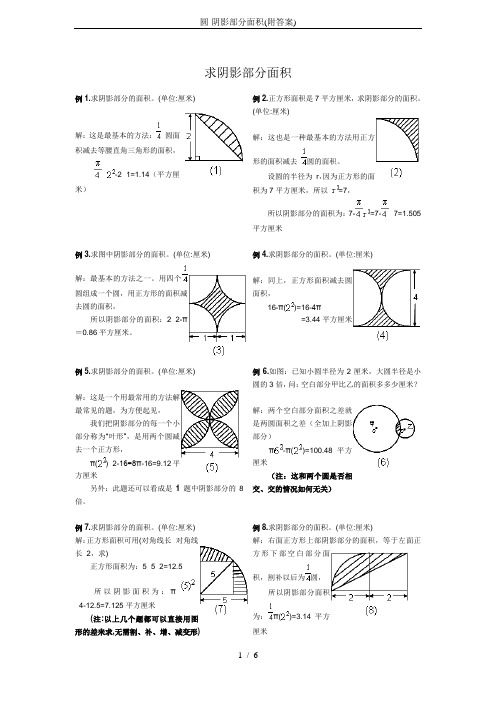
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
圆-阴影部分面积(含答案).
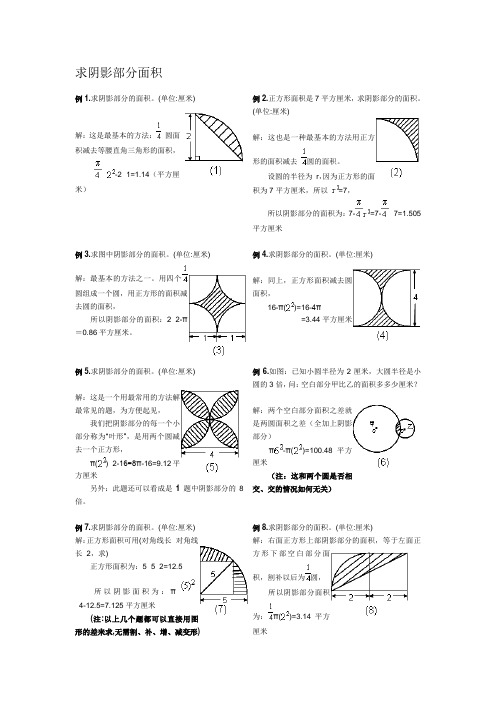
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
圆与三角形求阴影面积

圆与三角形求阴影面积1. 首先,让我们讨论如何计算圆的阴影面积。
一个圆的阴影面积是指圆周围的区域,被另一个对象(例如墙壁或其他物体)遮挡而无法被光线照射到的部分。
要计算圆的阴影面积,我们需要知道圆的半径和光源的位置。
2. 假设我们有一个圆,半径为R,光源位于圆心的正上方,距离为h。
为了计算阴影面积,我们首先需要确定光线从圆心到光源的投影长度。
这个投影长度可以通过简单的三角几何关系来计算。
由于光源位于圆心的正上方,光线与圆的切线垂直。
因此,光线的投影长度等于光线和圆的切线之间的距离。
3. 在这种情况下,投影长度等于圆的半径R。
因此,我们可以将投影长度定义为p=R。
接下来,我们需要计算投影长度与光源距离之间的比例。
这个比例可以通过简单的几何关系获得,即投影长度与光源距离之比等于圆的半径与光源距离之比。
4. 因此,我们可以得到以下比例:p/h=R/d,其中d是光源与圆心之间的距离。
通过重新排列这个方程,我们可以解出d:d=R*h/p。
5. 有了光源距离d,我们可以计算出阴影面积。
阴影面积等于圆的面积减去被光源照射到的部分的面积。
被光源照射到的部分是一个扇形,其角度等于2arcsin(p/d),其中arcsin是反正弦函数。
扇形的面积可以通过以下公式计算:A=πR²*θ/360°,其中A是扇形的面积,θ是扇形的角度。
6. 最后,我们可以计算阴影面积:阴影面积=圆的面积-扇形的面积。
圆的面积可以通过公式A=πR²计算得出。
将扇形的面积带入计算公式之后,我们可以得出最终的阴影面积。
总结:计算圆的阴影面积涉及到确定光源位置和圆的半径,以及计算光源距离和投影长度。
通过使用几何关系和公式,我们可以计算出阴影面积。
阴影面积等于圆的面积减去被光源照射到的部分的面积,其中被照射到的部分是一个扇形,其角度可以通过反正弦函数计算得到。
计算出阴影面积后,我们可以得到圆与光源的阴影面积。
求与圆有关的阴影部分面积

圆环面积=大圆面积 — 小圆面积 =R2×3.14-r2×3.14 =3.14×(R2-r2) =3.14×50 =157(平方厘米)
典型例题三、
3.如图,阴影面积是5cm2, 求圆环面积?
1 R2 1 r2 5cm2 22 R2 r2 10cm2 3.1410 31.4cm2
16π=50.24 25π=78.5
112 121
122 144 132 169 142 196
2
15 225 252 625
巧思巧解
圆的半径R=正方形的边长
R2 正方形的面积
大圆的半径R=大正方形的边长 小圆的半径r=小正方形的边长
R2 r 2 大正方形面积—小正方形面积
典型例题一、
求与圆有关的阴影部分面积
博尔思教育 胡亚静
CONTENTS
目 录
1 圆面积的基本知识 2 常用数据 3 典型例题:1、2、3、4
一、圆面积的基本知识
圆的面积S= r2
圆环面积S= (R2 r2 )
r r
二3π=9.42 4π=12.56 5π=15.7 6π=18.84 7π=21.98 8π=25.12 9π=28.26 10π=31.4
已知阴影部分的面积是20平 方厘米,圆的面积是多少?
分析:1.阴影部分面积是20平方厘米 2.正方形的边长=圆的半径 因此正方的面积=半径的平方
解:圆的面积=3.14×20=62.8平方厘米
典型例题二、
2.下图中阴影部分的面积是50 平方厘米,求环形的面积?
解:设大圆半径为 R,小圆半径为 r
典型例题四
4、如图,阴影面积是20cm2, 求圆环面积?
1 R2 1 r2 20cm2 22 R2 r2 40cm2 3.14 40 125.6cm2 125.6 3 94.2cm2
圆的面积和阴影面积计算

成成小升初精英班专享圆的面积计算(三分钟限时训练)——————你们这么萌!一定可以的!一、填空1、用圆规画一个周长69.08厘米的圆,圆规两脚之间的距离是()厘米,所画的圆的面积是()平方厘米。
2、圆的半径扩大6倍,直径扩大()倍,周长扩大()倍;面积扩大()倍。
3、一根铁丝正好围成一个直径3米的圆,这根铁丝长()米;如果改围成一个正方形,正方形的边长是()米,面积是()平方米。
4、小圆半径6厘米,大圆半径8厘米,两个圆重叠在一起,圆环的面积是()。
5、用一根长5米的绳子画一个最大的圆,这个圆的半径()米,周长()米,面积()平方米。
6、圆规两脚间距离5厘米,画出圆的周长()厘米,面积()平方厘米。
7、在一张长60厘米宽40厘米的长方形纸上剪一个最大的圆,圆的半径()厘米,周长()厘米,面积()平方厘米。
8、一个圆的半径扩大4倍,它的周长扩大()倍;面积扩大()倍。
9、在同一个圆中,所有的()都相等;所有的()都相等。
它俩之间的关系可以用()表示;也可以用()表示。
二、判断1、直径一定会半径长。
()2、一个圆的面积和一个正方形的面积相等,它们的周长一定也相等 ( )3、半圆的周长是这个圆的周长的一半。
()4、两端都在圆上的所有线段中,直径是最长的一条。
()5、同一个圆的直径一定是半径的2倍。
()6、圆只有一条对称轴。
()7、两个半圆的周长等于一个圆的周长()8、圆心决定圆的位置,半径决定圆的大小。
()三、应用题1、光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm,圆环的面积是多少平方厘米?2、下图中正方形的面积是8平方分米,那么圆的面积是多少?3、如图,在一块面积为12.56平方厘米的纸板中,裁出了2个同样大小的圆纸板。
问:余下的纸板的总面积是多少平方厘米?4、成成小升初精英班专享圆的面积计算(三分钟限时训练)——————你们这么萌!一定可以的!1、如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
(六年级)求阴影部分面积(圆和扇形)

2020年3月5日星期四
10m2
竹溪县实验小学 吴怀忠
3 求阴影部分的周长与面积。(单位:cm
4
10
2020年3月5日星期四
竹溪县实验小学 吴怀忠
4 求阴影部分周长和 面积。(单位:dm)
3
2020年3月5日星期四
5
竹溪县实验小学 吴怀忠
5 求阴影部分面积。(单位:dm)
8 求阴影部分周长和 面积。(单位:cm)
4
2020年3月5日星期四
2
竹溪县实验小学 吴怀忠
9 跑道外圈长多少米?内圈长 多少米?(两端各是半圆) 跑道和草坪面积分别是多少?
2020年3月5日星期四
100米
竹溪县实验小学 吴怀忠
10 求阴影部分面积。
2020年3月5日星期四
4cm
竹溪县实验小学 吴怀忠
11 求阴影部分面积。
2020年3月5日星期四
4m
4m
竹溪县实验小学 吴怀忠
8
2020年3月5日星期四
竹溪县实验小学 吴怀忠
10
10
用割补法:阴影部分的面积=圆面积的一半
求阴影部分的周长和面积。
6dm
求阴影部分周长和 面积。(单位:cm)
20
右面图形的中间是一个 边长为4厘米的正方形。 计算整个图形的面积是 多少平方厘米?
=
+
求阴影面积: 直接算呢?有简便方法吗?
4cm 4cm
求下列各图中阴影部分面积。
阴影部分的面积 =大半圆的面积 -小半圆的面积
一、复习
1、求圆面积的计算公式。 S = πr2
2、求正方形面积的计算公式。 S = a2
3、求三角形面积的计算公式。 S = a×h÷2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成成小升初精英班专享圆的面积计算(三分钟限时训练)
——————你们这么萌!一定可以的!
一、填空
1、用圆规画一个周长69.08厘米的圆,圆规两脚之间的距离是()厘米,所画的圆
的面积是()平方厘米。
2、圆的半径扩大6倍,直径扩大()倍,周长扩大()倍;面积扩大()倍。
3、一根铁丝正好围成一个直径3米的圆,这根铁丝长()米;如果改围成一个正
方形,正方形的边长是()米,面积是()平方米。
4、小圆半径6厘米,大圆半径8厘米,两个圆重叠在一起,圆环的面积是()。
5、用一根长5米的绳子画一个最大的圆,这个圆的半径()米,周长()米,
面积()平方米。
6、圆规两脚间距离5厘米,画出圆的周长()厘米,面积()平方厘米。
7、在一张长60厘米宽40厘米的长方形纸上剪一个最大的圆,圆的半径()厘米,周
长()厘米,面积()平方厘米。
8、一个圆的半径扩大4倍,它的周长扩大()倍;面积扩大()倍。
9、在同一个圆中,所有的()都相等;所有的()都相等。
它俩之间的
关系可以用()表示;也可以用()表示。
二、判断
1、直径一定会半径长。
()
2、一个圆的面积和一个正方形的面积相等,它们的周长一定也相等 ( )
3、半圆的周长是这个圆的周长的一半。
()
4、两端都在圆上的所有线段中,直径是最长的一条。
()
5、同一个圆的直径一定是半径的2倍。
()
6、圆只有一条对称轴。
()
7、两个半圆的周长等于一个圆的周长()
8、圆心决定圆的位置,半径决定圆的大小。
()
三、应用题
1、光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm,圆环的面积是多少平方
厘米?
2、下图中正方形的面积是8平方分米,那么圆的面积是多少?
3、如图,在一块面积为12.56平方厘米的纸板中,裁出了2个同样大小的圆纸板。
问:余下的纸板的总面积是多少平方厘米?
4、
成成小升初精英班专享圆的面积计算(三分钟限时训练)
——————你们这么萌!一定可以的!
1、如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
2、正方形边长为2厘米,求阴影部分的面积。
3、图中四个圆的半径都是1厘米,求阴影部分的面积。
4、如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)
分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,
5、求阴影部分的面积。
(单位:厘米)
6、如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
