第三章-命题逻辑的推理理论
合集下载
命题逻辑的推理理论,证明方法
31
⑨p
前提引入
⑩ pp
⑧⑨合取
推理正确, q是有效结论
.
武汉大学国际软件学院
唐存琛 刘峰
32
课堂实训
应用实例1 分析下列事实“如果我有很高的收 入，那么我就能资助许多贫困学生；如果我能资 助许多贫困学生，那么我很高兴；但我不高兴， 所以我没有很高的收入。”试指明前提和结论， 并给予证明。
.
武汉大学国际软件学院
.
武汉大学国际软件学院
唐存琛 刘峰
20
归谬法(反证法)的说明
欲证明
前提：A1, A2, … , Ak 结论：B
将B加入前提, 若推出矛盾, 则得证推理正确.
理由: A1A2…AkB (A1A2…Ak)B (A1A2…AkB)
括号内部为矛盾式当且仅当 (A1A2…AkB)为重言式
.
武汉大学国际软件学院
12
一、自然推理系统P的定义（续）
3. 推理规则 (1) 前提引入规则 (2) 结论引入规则 (3) 置换规则 (4) 假言推理规则 (5) 附加规则 (6) 化简规则
(7) 拒取式规则 (8) 假言三段论规则 (9) 析取三段论规则 (10)构造性二难推理
规则 (11) 破坏性二难推理
规则 (12) 合取引入规则
.
武汉大学国际软件学院
唐存琛 刘峰
16
（5）分情况证明法
为了证明 A1 A2 An B , 只需证明对任意的 i (1 i n) ，均有 Ai B 。
（6）附加前提证明法
为了证明 A1 A2 An A B ,
只需证明 A1 A2 An A B
.
武汉大学国际软件学院
武汉大学国际软件学院唐存琛 刘峰
离散数学课件03命题逻辑的推理理论
((┐p∧┐q)∨p) ∨ q
((┐p∨p )∧(┐q∨p)) ∨ q
(┐q∨p) ∨ q 1
精选课件ppt
由定理 3.1可知， 推理正确。
15
推理定律--重言蕴含式
(1) A (A∨B)
附加律
(2) (A∧B) A
化简律
(3) (A→B)∧A B
假言推理
(4) (A→B)∧┐B ┐A
拒取式
(5) (A∨B)∧┐B A
析取三段论
(6) (A→B) ∧ (B→C) (A→C)
假言三段论
(7) (AB) ∧ (BC) (A C)
等价三段论
(8) (A→B)∧(C→D)∧(A∨C) (B∨D) (A→B)∧(┐A→B)∧(A∨┐A) B
构造性二难 构造性二难
(特殊形式)
(9)(A→B)∧(C→D)∧(┐B∨┐精D选)课件pp(t ┐A∨┐C) 破坏性二难16
只要不出现(3)中的情况，推理就是正确的，因而判断 推理是否正确，就是判断是否会出现(3)中的情况。
推理正确，并不能保证结论B一定为真。
精选课件ppt
8
例题
例3.1 判断下列推理是否正确。（真值表法）
(1) {p,p→q}├ q (2) {p,q→p}├ q
正确 不正确
p q p(p→q) q p(q→p)
推理是指从前提出发推出结论的思维过程。
前提是已知命题公式集合。
结论是从前提出发应用推理规则推出的命题公式。
证明是描述推理正确或错误的过程。
要研究推理，首先应该明确什么样的推理是有效的或 正确的。
精选课件ppt
4
命题逻辑的推理理论
概念
描述问题 的句子
命题逻辑的推理理论课件(离散数学)
21
一、自然推理系统P
自然推理系统P由三个部分组成：
1.
字母表：命题变项符号；联结词符号；括
号和逗号。
2.
命题公式。
3.
推理规则。
22
二、推理规则
(1) 前提引入规则 (2) 结论引入规则 (3) 置换规则 (4) 假言推理规则 AB A \B (5) 附加规则 A \AB (6) 化简规则 AB \A (7) 拒取式规则 AB B \A (8) 假言三段论规则 AB BC \AC
30
四、附加前提证明法
例6：用附加前提证明法构造证明下面的推
理： 2是素数或合数。若2是素数，则 2 是 无理数。若 2 是无理数，则4不是素数。所 以，如果4是素数，则2是合数。
31
四、附加前提证明法
解： 设 p：2是素数， q：2是合数，
r： 2 是无理数，s：4是素数 推理形式结构 前提：pq, pr, rs 结论：sq
40
五、归谬法
解：命题符号化
p：小张守第一垒 q：小李向B队投球
r：A队取胜
s：A队成为联赛第一名
推理的形式结构如下：
( p q ) r , r s , s , p 结论： q
前提：
41
五、归谬法
证一：归谬法（略） 证二：直接法 ① r s 前提引入
② s
③r
前提引入
5
前提是有限个公式的集合，而不是序列 。
二、推理的有效性
A1A2… Ak
0 0
B
0 1
推理的有效性 有效 有效
1
1
0
有效
无效
6
二、推理的有效性
定义：若对于每组赋值，当 A1A2…Ak
一、自然推理系统P
自然推理系统P由三个部分组成：
1.
字母表：命题变项符号；联结词符号；括
号和逗号。
2.
命题公式。
3.
推理规则。
22
二、推理规则
(1) 前提引入规则 (2) 结论引入规则 (3) 置换规则 (4) 假言推理规则 AB A \B (5) 附加规则 A \AB (6) 化简规则 AB \A (7) 拒取式规则 AB B \A (8) 假言三段论规则 AB BC \AC
30
四、附加前提证明法
例6：用附加前提证明法构造证明下面的推
理： 2是素数或合数。若2是素数，则 2 是 无理数。若 2 是无理数，则4不是素数。所 以，如果4是素数，则2是合数。
31
四、附加前提证明法
解： 设 p：2是素数， q：2是合数，
r： 2 是无理数，s：4是素数 推理形式结构 前提：pq, pr, rs 结论：sq
40
五、归谬法
解：命题符号化
p：小张守第一垒 q：小李向B队投球
r：A队取胜
s：A队成为联赛第一名
推理的形式结构如下：
( p q ) r , r s , s , p 结论： q
前提：
41
五、归谬法
证一：归谬法（略） 证二：直接法 ① r s 前提引入
② s
③r
前提引入
5
前提是有限个公式的集合，而不是序列 。
二、推理的有效性
A1A2… Ak
0 0
B
0 1
推理的有效性 有效 有效
1
1
0
有效
无效
6
二、推理的有效性
定义：若对于每组赋值，当 A1A2…Ak
命题逻辑的推理理论
前提引入 ①化简 ①化简 前提引入 ②④假言推理 前提引入 ③⑥假言推理 ⑤⑦析取三段论
29
附加前提法
有时推理旳形式构造具有如下形式 ： 前提：A1, A2, …, Ak 结论：CB
可将结论中旳前件也作为推理旳前提，使结论只为B。 前提：A1, A2, …, Ak, C 结论：B
理由： (A1A2…Ak)(CB) ( A1A2…Ak)(CB) ( A1A2…AkC)B (A1A2…AkC)B
当推理中包括旳命题变项较多时，上述三种措施演 算量太大。
对于由前提A1,A2,…,Ak推B旳正确推理应该给出严谨 旳证明。
证明是一种描述推理过程旳命题公式序列，其中旳 每个公式或者是前提，或者是由某些前提应用推理 规则得到旳结论（中间结论或推理中旳结论）。
要构造出严谨旳证明就必须在形式系统中进行。
31
例题
（2） 形式构造：
前提：(p∧q)→r,┐s∨p,q 结论：s→r
（3）证明：用附加前提证明法
①s
附加前提引入
② ┐s∨p
前提引入
③p
①②析取三段论
④ (p∧q)→r
前提引入
⑤q
前提引入
⑥ p∧q
③⑤合取
⑦r
④⑥假言推理
32
归谬法（反证法）
有时推理旳形式构造具有如下形式：
前提：A1, A2, …, Ak 结论：B
只要不出现(3)中旳情况，推理就是正确旳，因而判断 推理是否正确，就是判断是否会出现(3)中旳情况。
推理正确，并不能确保结论B一定为真。
7
例题
例3.1 判断下列推理是否正确。（真值表法）
(1) {p,p→q}├ q (2) {p,q→p}├ q
离散数学课件-3-命题逻辑的推理理论
第三章 命题逻辑的推理理论§1 推理的形式结构推理：从前提出发推出结论的思维过程。
前提：已知命题公式集合。
结论：从前提出发应用推理规则推出的命题公式。
定义设A1, A2, …, A k, B都是命题公式，若命题公式A1∧A2∧…∧A k→B是重言式，则称由前提A1, A2, …, A k推出结论B的推理是有效的或正确的，并称B是有效的结论。
推理的形式结构记为{A1,A2,…,A k}A B推理正确，记为{ A1,A2,…,A k }⊨B推理无效，记为{ A1,A2,…,A k }⊭B注①推理正确，结论未必为真。
②推理只注重结构。
例判断下述推理的正确性。
(1) {p, p→q}⊢ q(2) {p, q→p}⊢ q解 (1) p∧(p→q)→q⇔p∧(¬p∨q)→q⇔(p∧¬p)∨(p∧q)→q⇔p∧q→q⇔¬ (p∧q)∨q⇔¬p∨(¬q∨q)⇔¬p∨1⇔1故{p, p→q }⊨ q(2) p∧(q→p)→q让q =0，可得q→p =1，再取p =1可得p∧(q→p)=1 由此得p∧(q→p)→q有成假赋值1 0，故{ p, q→p }⊭ q判断推理正确性：1．真值表法。
2．等值演算法。
3．主析取范式法。
4．构造证明。
例判断下述推理是否正确？（1）若a能被4整除，则a能被2整除。
a能被4整除。
所以a能被2整除。
（2）若下午气温超过30℃，则王小燕必去游泳。
若她去游泳，则她就不去看电影了。
所以，若王小燕没去看电影，则下午气温必超过了30℃。
解(1) p：a能被4整除q：a能被2整除前提：p→q，p结论：q推理的形式结构：{p→q，p} A q前面已证此推理正确。
(2) p：下午气温超过30℃q：王小燕去游泳r：王小燕去看电影前提：p→q, q→¬r结论：¬ r→p推理的形式结构：{p→q，q→¬r} A(¬r→p)因为，(p→q)∧(q→¬ r)→(¬r→p)⇔m1∨m3∨m4∨m5∨m6∨m7主析取范式显然不是重言式，故推理不正确。
3 命题逻辑的推理理论
（7）拒取式规则
AB B A
（8） 假言三段论规则
AB BC AC
（9）析取三段论规则
AB B A
（10）构造性二难推理规则
AB CD AC BD
（11）破坏性二难推理规则
AB CD BD AC
（12） 合取引入规则
A B AB
证明方法： ◦ 直接证明法 ◦ 附加前提法 ◦ 归谬法（或称反证法）
（2） 联结词符号： ┐， ， ， ， （3） 括号与逗号：( )，， 2. 合式公式（同合取联接词定义）
3. 推理规则
（1）前提引入规则 在证明的任何步骤上都可以引入前提。
（2）结论引入规则 在证明的任何步骤上所得到的结论都可以作为后继证明的前提。
（3）置换规则 在证明的任何步骤上，命题公式中的子公式都可以用与之等值的公
1、用不同的方法验证下面推理是否正确。对于正确的推理还 要在P系统中给出证明。 （1） 前提：pq, q
结论：p （2） 前提：qr, pr
结论：qp
（1）不正确。 验证答案，只需证明(pq)qp不是重言式。 方法一 等值演算
(pq)qp ((pq)q)p (pq)qp ((pq)(qq))p pq 易知10是成假赋值，故(pq)qp不是重言式，所以推理不正确。
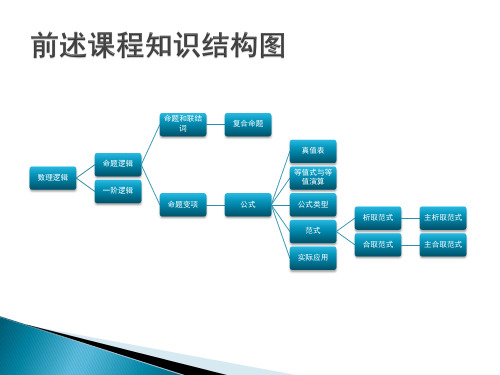
数理逻辑
命题逻辑 一阶逻辑
命题和联结 词
命题变项
复合命题 公式
真值表 等值式与等
值演算 公式类型
范式
实际应用
析取范式 合取范式
主析取范式 主合取范式
根据下列真语句，请判断是谁谋害了张先生？ (1)A、B、C三人中至少有一人。 (2)如果张先生生前未饮过麻醉剂，那不是C。 (3)如果张先生曾饮过麻醉剂，那不是A。 (4)如果是A谋害的，那么B也参加了。 (5)如果作案在落雨前，则是A谋害的。 (6)如果作案不在落雨前，张先生临死前搏斗过。 (7)张先生临死前搏斗过，就不是B谋害的。 (8)经过法医解剖化验，张先生死前曾饮过麻醉剂。
3第三章 命题逻辑的推理理论
从语言角度, 推理分为语义和语法两种。 从语言角度, 推理分为语义和语法两种。 语义(semantics)推理注重内涵的正确性 也就是从真 语义(semantics)推理注重内涵的正确性, 也就是从真 推理注重内涵的正确性, 要推出真的结论来, 的前提出发要推出真的结论来 推理过程考虑得少, 的前提出发要推出真的结论来, 推理过程考虑得少,关 心的是结论的正确性。 心的是结论的正确性。 语法推理则注重形式上的有效, 注重推理过程是否符 语法推理则注重形式上的有效, 注重推理过程是否符 则注重形式上的有效 合某些事先规定的逻辑规则, 结论是严格遵循规则 合某些事先规定的逻辑规则, 若结论是严格遵循规则 有效的 得到的, 那便是有效 得到的, 那便是有效的。 数理逻辑主要采用语法推理, 数理逻辑主要采用语法推理, 它关心的是结论的有效 不关心前提的实际真值, 性，而不关心前提的实际真值, 当然语法推理作为一 种推理方法, 种推理方法, 它必须能反映客观事物中真实存在的逻 辑关系, 语法推理必须保证语义上的正确性 必须保证语义上的正确性。 辑关系, 即 语法推理必须保证语义上的正确性。
3、2.1节给出的24个等值式中的每个都可以 2.1节给出的 个等值式中的每个都可以 节给出的24 派生出两条推理定律。 派生出两条推理定律。 例如：双重否定律 A⇔¬¬A ⇔¬¬A 例如： 可以产生两条推理定律 A⇒¬¬A ¬¬A ¬¬A ¬¬A ⇒A
§3.2 自然推理系统P 自然推理系统P
由上一节知识可知，可以利用真值表法、等值演算法 由上一节知识可知，可以利用真值表法、 真值表法 和主析取范式法三种方法来判断推理是否正确。 和主析取范式法三种方法来判断推理是否正确。 三种方法来判断推理是否正确 但是，当推理中包含的命题变项较多时，以上三种 命题变项较多时 但是，当推理中包含的命题变项较多 方法的演算量太大。因此对于由前提A1, A2,…,Ak推 方法的演算量太大。因此对于由前提A B的正确推理应给出严谨的证明。 正确推理应给出严谨的证明。 证明是一个描述推理过程的命题公式序列， 证明是一个描述推理过程的命题公式序列，其中的每 是一个描述推理过程的命题公式序列 个公式是已知前提或者是由某些前提应用推理规则得 个公式是已知前提或者是由某些前提应用推理规则得 已知前提或者是 到的结论。 到的结论。
命题逻辑的推理理论
精品课件
精品课件
实例
例 判断下面推理是否正确 (1) 若今天是1号，则明天是5号. 今天是1号. 所 以明天是5号.
解 设 p：今天是1号，q：明天是5号. 证明的形式结构为: (p®q)Ùp®q
证明（用等值演算法）
(p®q)Ùp®q Û Ø((ØpÚq)Ùp)Úq Û ØpÚØqÚq Û 1
得证推理正确
A Þ (AÚB)
附加律
(AÙB) Þ A
化简律
(A®B)ÙA Þ B
假言推理
(A®B)ÙØB Þ ØA
拒取式
(AÚB)ÙØB Þ A
论
析取三段
(A®B)Ù(B®C) Þ (A®C)
假言三段论
(A«B)Ù(B«C) Þ (A«C)
等价三段论
(A®B)Ù(C®D)Ù(AÚC) Þ (BÚD)
难
构造性二
推理的形式结构。
精品课件
说明（2）
设任一A1组，赋A2值，a…1a，2…Aka，n （B中ai＝共0出或现1n，个命i＝题1变，项2，，…对n于），
前提和结论的取值情况有以下四种：
（1） A1ÙA2Ù…ÙAk 为0，B为0； （2） A1ÙA2Ù…ÙAk 为0，B为1； （3） A1ÙA2Ù…ÙAk 为1，B为0； （4） A1ÙA2Ù…ÙAk 为1，B为1。
AB
(12) 合取引入规则
CD
课件
构造证明——直接证明法
例3.3 在自然推理系统P中构造下面推理的证明；
（1） 前提：p Ú q， q ® r， p ® s ， Ø s 结论：r Ù （p Ú q）
（2）前提： Ø p Ú q， r Ú Ø q ，r ® s 结论：p ® s
精品课件
精品课件
实例
例 判断下面推理是否正确 (1) 若今天是1号，则明天是5号. 今天是1号. 所 以明天是5号.
解 设 p：今天是1号，q：明天是5号. 证明的形式结构为: (p®q)Ùp®q
证明（用等值演算法）
(p®q)Ùp®q Û Ø((ØpÚq)Ùp)Úq Û ØpÚØqÚq Û 1
得证推理正确
A Þ (AÚB)
附加律
(AÙB) Þ A
化简律
(A®B)ÙA Þ B
假言推理
(A®B)ÙØB Þ ØA
拒取式
(AÚB)ÙØB Þ A
论
析取三段
(A®B)Ù(B®C) Þ (A®C)
假言三段论
(A«B)Ù(B«C) Þ (A«C)
等价三段论
(A®B)Ù(C®D)Ù(AÚC) Þ (BÚD)
难
构造性二
推理的形式结构。
精品课件
说明（2）
设任一A1组，赋A2值，a…1a，2…Aka，n （B中ai＝共0出或现1n，个命i＝题1变，项2，，…对n于），
前提和结论的取值情况有以下四种：
（1） A1ÙA2Ù…ÙAk 为0，B为0； （2） A1ÙA2Ù…ÙAk 为0，B为1； （3） A1ÙA2Ù…ÙAk 为1，B为0； （4） A1ÙA2Ù…ÙAk 为1，B为1。
AB
(12) 合取引入规则
CD
课件
构造证明——直接证明法
例3.3 在自然推理系统P中构造下面推理的证明；
（1） 前提：p Ú q， q ® r， p ® s ， Ø s 结论：r Ù （p Ú q）
（2）前提： Ø p Ú q， r Ú Ø q ，r ® s 结论：p ® s
精品课件
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2．推理规则 （1）P 规则（前提引入规则）
在推导过程中，前提可视需要引入使用。前提可 以用在证明中的任何步骤上。
（2）T规则 （结论引入规则）
在推导过程中，利用推理定律可引入前面已导出 结论的有效结论。
3. CP规则 (附加前提规则)
（1）欲证： 前提：A1, A2, …, Ak 结论：CB （3）理由： (A1A2…Ak)(CB) （2）等价地证明 前提: A1, A2, …, Ak, C
假言推理
拒取式 析取三段论
(AB)(BC) (AC)
(AB)(BC) (AC) (AB)(CD)(AC) (BD) (AB)(AB)(AA)B
假言三段论
等价三段论 构造性二难 构造性二难(特殊形式)
(AB)(CD)( BD) (AC) 破坏性二难
析取三段论
A B
B
A
构造性二难：
AB CD AC BD
合取引入： A B A B
破坏性二难： AB CD BD AC
（1）推理定律——重言蕴涵式
A (AB) (AB) A 附加律 化简律
(AB)A B
(AB)B A (AB)B A
3．判断推理是否有效的方法（多种） （1）真值表法 （2）等值演算法 （3）主析取范式法
例 判断下面推理是否正确? （1）若今天是1号，则明天是5号. 今天是1号. 所以明天是5号. （2）若今天是1号，则明天是5号. 明天是5号. 所以今天是1号. 解 设p：今天是1号，q：明天是5号. 证明的形式结构采用（2）.
第三章 小 结 一、本章的主要内容及要求 1．主要内容 推理的形式结构的不同形式 判断推理是否正确的不同方法 ① 真值表法 ② 等值演算法
③ 主析取范式法
④ 形式证明…
2. 要求
理解并记住推理形式结构的如下形式：
① (A1A2…Ak)B
② 前提：A1, A2, … , Ak
结论：B
熟练掌握判断推理是否有效的不同方法（如真 值表法、等值演算法、主析取范式法等） 牢记P系统中各条推理规则（内容与名称）
P P
③ r
④ (p q ) r
T①②拒取式
P
⑤ (p q )
T ③④拒取式
例 构造下面推理的证明： 2是素数或合数. 若2是素数，则 2 是无理数. 若 2 是无理数，则4不是素数. 所以，如果4是 素数，则2是合数. 用附加前提证明法构造证明 （1）设p：2是素数，q：2是合数，
练习： 3.如果乐队不能演奏摇滚乐或者点心没有 准时送上来，那么新年音乐会就将取消， 并且玛丽会很生气。如果音乐会取消， 那么就要办理退款。没有办理退款。所 以乐队能演奏摇滚乐。
练习： 证明： (1)pq，(qr)r，(ps)s (2) (pq) (qr) p
前提：A1, A2, … , Ak
结论：B
（2）将B当前提，推出矛盾，得证（1）正确 （3）理由： A1A2…AkB (A1A2…Ak)B (A1A2…AkB) 括号内部为矛盾式当且仅当 (A1A2…AkB)为 重言式
例 前提： (pq)r, rs, s, p 结论：q
r： 2 是无理数， s：4是素数
（2）形式结构 前提：pq, pr, rs 结论：sq
（3）证明 ①s ② p r ③ rs ④ ps ⑤ p CP P P T②③假言三段论 T①④拒取式
⑥ p q
⑦q
P
T⑤⑥析取三段论
请用直接证明法证明之
4．归谬法（或称反证法）
（1）欲证 A1A2…AkB
P T (1)蕴含等值式 P T(2) (3) 假言三段论 T(4) 假言异位 P T(5)(6)假言三段论 T(7) 蕴含等值式
例：前提：pq,q(rs),r(t u), pt
结论：u (1)pq
(2)q(rs) (3)p(rs) (4)pt (5)p (6) (rs)
((pq)q)p
(pq)qp
((pq)(qq))p
p q 易知10是成假赋值，故()不是重言式，所以推理不正确.
方法二 主析取范式法 经过演算后可知 () m0m1m3 未含m2, 故()不是重言式.
方法三 真值表法，()的真值表为
p q 0 0 1 1 0 1 0 1 (pq)qp 1 1 0 1
结论（不正确）是对的 方法四 直接观察出10是成假赋值
解（2）答案：推理正确
方法一 真值表法（自己做）
方法二 等值演算法（自己做） 方法三 主析取范式法（自己做）
方法四 P系统中构造证明
证明：（直接证明法）
① pr （前提引入）
T③⑥析取三段论
T⑦附加
② rp ③ qr ④ qp （①置换） （前提引入） （③②假言三段论） 请用附加前 提证明法证 明之
2．在P系统中构造下面推理的证明： 如果今天是周六，我们就到颐和园或圆明 园玩. 如果颐和园游人太多，就不去颐和 园. 今天是周六，并且颐和园游人太多. 所 以我们去圆明园或动物园玩.
结论： B
( A1A2…Ak)(CB)
( A1A2…AkC)B
(A1A2…AkC)B
（1） pq （ 2） p q （ 3） q s （4） p s （ 5） s p （6） pr （7） s r （8） sr
三、构造证明 1．P规则（前提引入规则） 例：前提: (pq) , (pr) ,(qs) ； 结论: sr
若明天是星期一或星期三，我就有课。 若有 课，今天必备课。我今天下午没备课. 所以， 说明天是星期一或星期三是不对的。
构造证明（ 1 ）设 p ：明天是星期一， q ：明天 是星期三，r：我有课，s：我备课 （2）形式结构：
前提：(pq)r, rs, s
结论：(p用归缪法）
①q
② rs
结论否定引入
P
③ s
④ r ⑤ (pq)r ⑥ (pq)
P
T②③拒取式 P T④⑤析取三段论 T⑥置换 T①⑦析取三段论 P
请用直接证明法证 明之
⑦ pq ⑧ p ⑨p
⑩ pp
T⑧⑨合取
练习： 1.证明：(pr),qs ,p,q r∧s 2.在自然推理系统中构造下面推理的证明： 若小张喜欢数学，则小李或小赵也喜欢 数学。若小李喜欢数学，他也喜欢物理。 小张确实喜欢数学，可小李不喜欢物理， 所以小赵喜欢数学。
会用附加前提证明法及归谬法
二、练习
1．用不同的方法验证下面推理是否正确. 对于 正确的推理还要在P系统中给出证明.
（1）前提：pq, q 结论：p
（2）前提：qr, pr
结论：qp
解（ 1 ）答案：不正确。验证答案，需将推理形式结 构改为另一种形式 (pq)qp () 只需证明()不是重言式 方法一 等值演算 (pq)qp
P P T(1)(2)假言三段论 P T(4)化简律 T(5)(3)假言三段论
(7)r
(8) r(t u)
T(6)化简律
P
(9) (rt) u
(10) t
T(8)
T(4)化简律
(11) rt
(12) u
T(7) (10)合取
T(9) (11)析取三段论
例 用直接证明法构造下面推理的证明：
第1.5节 推理理论
本章的主要内容
推理的形式结构
形式证明
1 推理的形式结构 一、何为推理？
1．例 （1）若今天是星期一，则明天是星期二 （2）若ACBD，则AB且CD 2．推理——从前提出发推出结论的思维过程
上例中，（1）是有效的推理，而（2）是无效的 推理.
二、推理的形式结构及证明方法
（4）形式证明
形式证明的推理过程是一个命题序列，其中每个命题 或者是已知命题，或者是由某个前提根据推理规则推 出的结论，序列的最后一个命题是需要论证的结论。
1 推理定律
假言推理
AB A B
附加律
A AB
化简律 AB A
假言三段论
A B B C A C
拒取式 AB B A
（1）设 p：今天是周六， q：到颐和园玩， r：到圆明园玩， s：颐和园游人太多
（3）证明：
① p (q r) ②p ③ q r ④ sq P P T①②假言推理 P
t：到动物园玩
（2）前提：
⑤s
⑥ q
P
T ④⑤假言推理
p(qr), sq, p, s
结论：rt
⑦r
⑧ r t
1．推理的有效性 定义1 设A1, A2, …, Ak, B为命题公式
由前提A1, A2, …, Ak 推出结论B的推理形式表示为 （1）A1A2…AkB （符号表示推出） （2）前提： A1, A2, … , Ak 结论： B
2．推理的形式结构（多种形式）
定义2 若对于每组赋值，或者A1A2… Ak 均为假，或者当 A1A2…Ak 为真时， B 也为 真，则称由前提A1, A2, …, Ak推出B的推理是 有效的（正确），并称B是一组前提A1, A2, …, Ak 的有效结论；否则称推理是无效的（错误 的）。 定理1 命题公式A1, A2, …, Ak 推出B的推理 是有效的当且仅当 A1A2…AkB为重言式
（1）(pq)pq
（2）(pq)qp
证明（1）（用等值演算法） (pq)pq ((pq)p)q pqq 1 由定理1可知推理正确
证明：（2）（用主析取范式法） (pq)qp (pq)qp ((pq)q)p q p (pq)(pq) (pq)(pq) m0m2m3 结果不含m1, 故01是成假赋值,所以推理不正确