开环幅相曲线绘制
绘制开环幅相频率特性曲线的教学方法研究

2 0 1 3年 1 1 月 第3 1 卷 第 6 期
的交点 的确 定
特 性 曲线 与实轴 的交 点 : 由 Q( 叫 ) 一0求 出对 应
的 ∞的值 , 再将 叫值代入到 P( ) 表达式 中, 得到的 值 即为频率 特性 曲线 与 实轴交 点 的坐 标 ;
同理 , 特 性 曲线 与 虚 轴 的 交 点 : 由 P( ) = = = 0求 出对 应 的 的值 , 再将 ∞值代 入到 Q( ∞ ) 表达式中, 得 到 的值 即为频率 特性 曲线 与 虚轴 交点 的坐 标 。 注: 问断 点 的问题 。随 着 叫的值 从 0开 始 不 断 增加 , 系统 的频率 特 性 曲线 在 某一 点 或某 些 点 处 不 连续 , 特 别要 注 意这些 不 连续 点 , 参 看本 文 开环 幅相 频率 特 性 曲线绘 制举 例部 分 中 的例 4 。
和虚部 的值及正负性 , 确定起点坐标及所处的象限。 步骤 二 开环 幅 相频 率特性 曲线 终 点 的确定 将∞ 一+。 。 分别代入到系统频 率特性 表达式 中的 实部和虚部 , 分别 求 出实部 及虚部 的值 。根 据 实部 和 虚部 的值 及正负性 , 确定终点坐标及所处的象限 。 步 骤 三 开环 幅 相频 率 特 性 曲线 与 实轴 、 虚 轴
2 开 环幅 相频 率特 性 曲线 绘制举 例 例 1 某 0型 单 位 反 馈 系 统 G( S )一
[ 收稿 日期]2 o 1 3 一O 6 —1 O [ 基金项 目]安徽省 教 育厅 自然科 学 重点 科 研项 目 ( K J 2 O 1 3 A O 7 1 ) ; 安 徽 省质 量工 程 项 目( 2 0 1 0 0 7 5 7 ) ; 安 徽 建 筑 大学 教 学 研究 项 目
5.3.15.2.2开环幅相特性曲线学习资料

j
1)
2 (1
k
0.25 2 )(1 2 ) [(1
2.5 2 )
j(0.5 2 )]
Im[ GK ( j)] 0.5 2
0
,求得
2 x
0.5 ,因此求得幅相曲线与实轴得交点为:Re[GK ( jx )] 2.67k
概略幅相曲线见右图:
入坐标原点;
n m 2 时, G( j) 0 180 0 ,Nyquist图从负实轴的方向进
入坐标原点;
n m 3时, G( j) 0 270 0 ,Nyquist图从正虚轴的方向进
入坐标原点。
图2
3)穿越实轴的位置。
令频率特性 G( j) 的虚部为零,即 Im[G( j)] 0 ,并求得相应的频率 x ,然后将此频率 x 代入 频率特性G( j) 的实部,则 Re[G( jx )] 就是Nyquist图与实轴的交点。
图1
5.2.2 开环幅相特性曲线
三要素
2)终点确定。
Nyquist图的终点是 时 G( j) 在复平面上的位置。
G(
j)
b0 s m a0 s n
b1sm1 a1sn1
... ...
bm1s an1s
bm an
b0 a0
(
1 j)nm
b0 / a0 ( j)nm
(3)
n m 1时, G( j) 0 900 ,Nyquist图从负虚轴的方向进
1)起点确定。
Nyquist图的起点是 0 时 G( j0 ) 在复平面上
的位置。
G(
j0 )
(
K
j)
G0 (
j)
0
(
K
j)
(2)
系统开环频率特性的绘制

5.3 系统开环频率特性的绘制对自动控制系统进行频域分析时,通常是根据开环系统的频率特性来判断闭环系统的稳定性和估算闭环系统时域响应的各项性能指标,或者根据开环系统的频率特性绘制闭环系统的频率特性,然后再分析及估算时域性能指标。
因此,掌握开环系统的频率特性曲线的绘制和特点是十分重要的。
5.3.1 开环幅相曲线的绘制开环系统的幅相频率特性曲线简称为开环幅相曲线。
准确的开环幅相曲线可以根据系统的开环幅频特性和相频特性的表达式,用解析计算法绘制。
显然,这种方法比较麻烦。
在一般情况下,只需要绘制概略开环幅相曲线,概略开环幅相曲线的绘制方法比较简单,但是概略曲线应保持准确曲线的重要特征,并且在要研究的点附近有足够的准确性。
下面首先介绍幅相频率特性曲线的一般规律与特点,然后举例说明概略绘制开环幅相曲线的方法。
设系统开环传递函数的一般形式为)1()1()()(11++=∏∏-==s T s s K s H s G j vn j v mi i τ )(m n ≥ (5-49)式中,K 为开环增益;v 为系统中积分环节的个数。
则系统的开环频率特性为)1()()1()()(11∏∏-==++=v n j jvmi i Tj j j K j H j G ωωωτωω (5-50)1.开环幅相曲线的起点在低频段当0→ω时,由式(5-50)可得 )90(0lim)(lim)()(lim ︒⋅-→→→==v j vve Kj K j H j G ωωωωωωω (5-51)由式(5-51)可知,当0→ω时,开环幅相曲线的起点取决于开环传递函数中积分环节的个数v 和开环增益K ,参见图5-23(a )。
0型(v =0)系统,开环幅相曲线起始于实轴上的)0,(j K 点。
Ⅰ型(v =1)系统,开环幅相曲线起始于相角为︒-90的无穷远处。
当+→0ω时,曲线渐近于与虚轴的平行的直线,其横坐标[])()(Re lim 0ωωωj H j G V x +→= (5-52)Ⅱ型(v =2)系统,开环幅相曲线起始于相角为︒-180的无穷远处。
线性系统频域分析方法开环频率曲线绘制

与实轴交点:
G( j)H ( j) K (T ) j(1T2 ) (1 T 22 )
x
1
T
G( jx )H ( jx ) K
2020/5/24
5-3开环频率曲线的绘制
12
二、开环幅相曲线的绘制(5)
例5.设系统开环传递函数为
G(s)H
(s)
s(Ts
K 1)(s 2
试绘制系统开环概略幅相曲线。
穿越频率: x
(3)变化范围(象限和单调性)。
Im[G( jx )H ( jx )] 0
(x ) G( jx )H ( jx ) k ; k 0, 1, 2,ggg
ReG( jx )H( jx ) G( jx )H( jx )
2020/5/24
5-3开环频率曲线的绘制
8
二、开环幅相曲线的绘制(2)
6)积分环节 1/ s
7)微分环节 s
(0 1)
2020/5/24
5-3开环频率曲线的绘制
3
一、典型环节及其频率特性(2)
非最小相位系统环节 1)比例环节 K (K 0) 2)惯性环节 1 / (1 Ts) (T 0)
3)一阶微分环节 1 Ts (T 0) 4)振荡环节 1/ (s2 / n2 2 s / n 1) (n 0, 0 1)
5)二阶微分环节 s2 / n2 2 s / n 1 (n 0,0 1)
2020/5/24
5-3开环频率曲线的绘制
4
一、典型环节及其频率特性(3)
Im
典型环节的幅相频率特性
⑴ 比例环节 G(s) K G( j) K
G K G 0
K Re
0 0
⑵ 微分环节 ⑶ 积分环节
第五章频率特性法

教学内容
1、频率特性的概念 2、典型环节频率特性
3、开环幅相曲线绘制方法,重点:开环对数频率特性曲线
4、频域稳定判据,奈奎斯特判据,对数频率稳定判据 5、稳定裕度的概念 6、闭环系统的频域指标
5-1 频率特性
频率特性法:用频率特性作为数学模型来分析和设 计系统的方法。 优点:①具有明确的物理意义; ②计算量很小,采用近似作图法,简单、直 观,易于在工程技术中使用; ③可以采用实验的方法求出系统或元件的频 率特性。
1 1 (T1 )
2
1 1 (T2 )
2
k
相频特性: ( ) tan1 T1 tan1 T2
1.确定开环幅相曲线的起点和终点
0时, G ( j 0) k (0) 0 时, G ( j 0) 0 (0) -180
式中, φ=-arctgωτ。
式(5.3)的等号右边 , 第一项是输出的暂态分量 , 第
二项是输出的稳态分量。 当时间t→∞ 时, 暂态分量趋 于零, 所以上述电路的稳态响应可以表示为
1 1 limuo (t ) sin( t ) U sin t (5.4) 2 2 t 1 j 1 j 1 U
0
ω 0 1/T ∞
∠G(jω ) 0º -90º -180º
│G(jω │ 1 1/2ζ 0
U(ω ) 1 0 0
V(ω )
-0.5
ζ =0.2— 0.8
0 -1/2ζ 0
-1.5 -0.5 0 0.5 1 1.5 -1
振荡环节的幅相曲线
: 0 , G ( j )曲 线 有 单 调 衰 减 和 谐 两 振种形式。
3、开环幅相曲线绘制开环幅相曲线绘制方法(1)由开环零点-极点
)
2型系统包含两个积分环节,例如
G(s)
K
s 2 (T1s 1)(T2 s 1)
G( j)
K
K
( j) 2 ( jT1 1)( jT2 1) 2 1 T12 2
() 180 arctgT1 arctgT2
2020/11/13
Automatic Control Theory
e j ( )
1 T22 2
起点: G( j0) A(0) K 终点: G( j) A() 0
G( j0) (0) 0o G( j) () 180o
与实轴的交点: Q(x ) 0 Q() K (T1 T2 ) /(1 T12 2 )(1 T22 2 ) 0
x 0
与虚轴的交点: P( y ) 0
P() K (1 T1T2 2 ) /(1 T12 2 )(1 T2 2 2 )
Hale Waihona Puke 变化的。例如P(0) K
0
G(s)
K(T1s 1)
(T2 s 1)(T3s 1)(T4 s 1)
n 3, m 1
G( j0) K0o , G( j) 0(1 3)90o 0 180o
2020/11/13
Automatic Control Theory
7
开环传递函数含有积分环节时的开环幅相曲线
T RC u r
C R uc
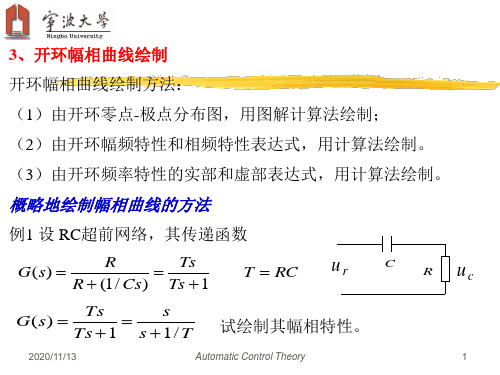
G(s) Ts s Ts 1 s 1/ T
试绘制其幅相特性。
2020/11/13
Automatic Control Theory
1
G( j) j T
T
j
(
arc
tgT
)
e2
jT 1 1 2T 2
关于绘制开环幅相频率特性曲线的方法研究

特性 曲线 的绘制则是利用乃奎斯特判据的基础 。针对许多学生对概念理解 不清的现状 , 本文着 重介绍绘制一般线性 系统开环幅相频率特性 曲
线 的原理 。 并分析其起点和终点的幅值与相位 , 详细阐述绘制步骤的推理过程 通过实例表 明, 该绘 制方法 简便 , 并且在教学 实践 中收 到了 良
Ab ta t Th t o ffe u n ya a y i o l e rs s e i av r sr c : e me h d o r q e c n l sst i a- y tm s e yi o t n eh di ls ia u o — n mp ra t t o ca sc l t ma m n a t n t e r ,a d t e Ny u i cie in i k y i e r i g a d ta h n . Dr wig t e c r e o g iu e i h o y n h q st rt r s e n lan n n e c i g o o a n h u v fma n t d - p a e fe u n y c aa trs i b s d o p n —lo sf u d t n o sn y u i cie in . I r e o h s rq e c h r ce it a e n o e c o p i o n a i fu ig N q st rt r o o n o d rt i r v h t d n s n e sa dn b u t o c p ,t i ril m p a ie rn i lso r wig c r e mp o e t e su e t ’u d r t n ig a o ti c n e t h sa t ee h sz sp icp e f a n u v s c d a o tg n r ll e rs se m a nt d p a e fe u n y c a a trsi n o e -o p.t e n lz s ma n — b u e e a i a- y t m g iu e h s r q e c h r ce it o p n l o n - c h n a ay e g i t d n h s fc r e Sp i a n e m ia.S m ee a p e n ia et a hsm e h d i s p ea dc n u ea dp a eo u v ’ r la d tr n 1 o x m lsid c t h tt i t o s i l n o — m m v n e t u t em o e i g t o d ta h n fe t e in ;f rh r r e sa g o e c i ge fc. t Ke w r s m a n f d p a efe u n y c a a trsi f p n lo ; y u s u v ;r q e c -il n l ss y o d : g i e — h s r q e c h r c eit o e -o p N q itc r e fe u n y f d a ay i i c o e
自动控制原理02开环幅相曲线、频域判据、闭环指标

代入 Re[G( j )] ,得:
10 Re[G( j)] 3
5.3.1 开环幅相曲线的绘制方法
最小相位系统的起点与终点:
G( j 0 )
{
K0, 0
( 900 ), 0
K *,n m
G( j)
{
0(n m)(900 ),n m
5.3.2 频率稳定判据
G( j 0 ) (90 ) G( j) 03(900 )
0
K s (T1s 1)(T2 s 1)
Im
Re
0
5.3.2 频率稳定判据
与坐标轴的交点
K [(T1 T2 ) j (1 T1T2 2 )] K G( j ) j ( jT1 1)( jT2 1) (1 2T12 )(1 2T2 2 )
5.3 开环幅相曲线与频域稳定判据
5.3.1 开环幅相曲线的绘制方法
绘制概略开环幅相曲线的步骤:
(1)求取系统的开环频率特性函数
(2)确定开环幅相曲线的起点和终点; (3)确定开环幅相曲线与实轴的交点; (4)勾画出大致曲线。 所用知识:复数的运算
5.3.1 开环幅相曲线的绘制方法
例5-3 已知系统的开环传递函数为 : G ( s ) 试绘制系统的开环幅相曲线
正穿越:开环幅相曲线从 上往下穿越实轴的 (1,) 区段(幅角增加) 负穿越:开环幅相曲线从 下往上穿越实轴的 (1,) 区段(幅角减小)
Nyquist图 以原点为圆心的单位圆 单位圆内 单位圆外 负实轴
Bode图 0dB线
L ( ) 0 的区段 L( ) 0 的区段
( ) 从下向上穿越 线 正穿越:从上往下穿越实轴 (1,) 区段 正穿越:在 L() 0 区段内, ( ) 从上向下穿越 线 负穿越:从下往上穿越实轴(1,) 区段 正穿越:在 L() 0 区段内,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
终点: G ( j∞) H ( j∞) = 0∠360 o
13
Automatic Control Theory
1
注意开环传递函数含有一个等幅振荡环节 当 ω = ωn
2 (s 2 / ω n ) + 1
A(ω n ) =| G ( jω n ) H ( jω n ) | → ∞
ϕ (ω n − ) ≈ −90 o − tg −1Tω n > −180 o ; ω n − = ω n − ε , ε > 0 ϕ (ω n + ) ≈ −90 o − tg −1Tω n − 180 o ; ω n + = ω n + ε , ε > 0
2012-4-26 Automatic Control Theory 10
j Im
起点与终点:
ω =0
Re 0ω → ∞
G ( j 0 + ) = ∞∠ − 180 o , G ( j∞) = 0∠ − 360 o
当包含一阶微分环节,这时的幅相曲 线也可能出现凹凸,例如
j Im
G (s) =
K (T3 s + 1) s 2 (T1 s + 1)(T 2 s + 1)(T 4 s + 1)
K G (s) = s (T1 s + 1)(T 2 s + 1)(T 3 s + 1)
假设 T 1 > T 2 > T 3 ,试概略绘制开环幅相曲线,并进行分析。
K G ( jω ) = jω ( jT1ω + 1)( jT 2 ω + 1)( jT 3ω + 1) = K
ω 1 + T1 2 ω 2 1 + T 2 2 ω 2 1 + T 3 2 ω 2
P(0) = K ω =0
n=2 n=4 n=3
ω → ∞ ∠G ( jω ) = (m − n) × 90
oLeabharlann 当开环传递函数包含有微分环节时,幅相 曲线会出现凹凸,幅值和相位不再是单调 ω →∞ 变化的。例如
K (T1 s + 1) G (s) = (T 2 s + 1)(T 3 s + 1)(T 4 s + 1)
2型系统包含两个积分环节,例如
G ( s) =
G( jω) =
K s 2 (T1 s + 1)(T2 s + 1) K
= K e jϕ (ω)
( jω) 2 ( jT1ω +1)( jT2ω +1)
ω 2 1+ T12ω 2 1+ T2 2ω 2
ϕ (ω ) = −180 − arctgT1ω − arctgT2ω
−90 −180 0 0 .1 −20
1
10
100
ω
−40
G ( jω )
ϕ (ω )
0
ω
∠G ( jω )
K K
, 1 / s , 1 /(Ts + 1) , 1 / jω , 1 /( jTω + 1)
绘制典型环节Bode图的数据: 20 log K = 20 log 7 = 16.9 (dB) 转折频率
2012-4-26
1 / T = 1 / 0.087 = 11.5 (rad / s )
16
Automatic Control Theory
ωT = 0
ωT →∞
2012-4-26
Automatic Control Theory
3
例2 某零型反馈控制系统,系统开环传递函数
K G ( s) = (T1 s + 1)(T2 s + 1)
试概略绘制系统的开环幅相曲线。
G ( jω ) =
G ( jω ) =
K = G ( jω ) e jϕ (ω ) = P (ω ) + jQ (ω ) ( jT1ω + 1)( jT2ω + 1)
Automatic Control Theory 9
令
Q (ω ) = 0 , ω x = 1 / T1T2 + T2 T3 + T3T1
− K (T1 + T 2 + T3 ) − ω x 2 T1T 2 T3
P (ω x ) =
[
]
(1 + T1 2 ω x 2 )(1 + T 2 2 ω x 2 )(1 + T3 2 ω x 2 )
i =1 i =1
对数幅频曲线和对数相频曲线是由n个典型环节对应曲线的叠加 后得到的。
2012-4-26 Automatic Control Theory 15
例1 设单位反馈系统,其开环传递函数
K G (s) = , s (Ts + 1)
K = 7, T = 0.087 s
试绘制近似对数幅频曲线和对数相频曲线,并修正近似对数幅频 曲线。 解:典型环节分别为
= = − K (T ω + j )
2 ω (1 + T 2 ω 2 )[1 − (ω 2 / ω n )]
− KT (1 + T ω )[1 − (ω
2 2 2 2 / ω n )]
+ j
−K
2 ω (1 + T 2 ω 2 )[1 − (ω 2 / ω n )]
起点: G ( j 0 + ) H ( j 0 + ) = ∞∠ − 90 o
ω =0
Re 0ω → ∞
起点与终点:
G ( j 0 + ) = ∞∠ − 180 o , G ( j∞) = 0∠ − 360 o
若T1大于其它时间常数,幅相曲线如图所示,与实轴、虚轴的 交点可以用对应的实部、虚部表达式求出。
2012-4-26 Automatic Control Theory 11
K (T 1 ω ) 2 + 1 ( T 2 ω ) 2 + 1
∠G( jω) = ϕ(ω) = −tg−1ω T1 − tg−1ω T2
实部与虚部
P(ω ) = K (1 − T1T2ω ) /(1 + T1 ω )(1 + T2 ω )
2 2 2 2 2
Q (ω ) = − K (T1 + T2 )ω /(1 + T1 ω )(1 + T2 ω 2 )
在 ω = ω n 附近,相角突变 -180o,幅相曲线在 ω = ω n 处出现了不连续
ω =∞ ω
ωn−
0
ω
ωn+
2012-4-26
Automatic Control Theory
14
4、开环对数频率特性曲线的绘制 、 设传递函数 G (s ) 由n个典型环节串联组成,n个典型积分环节分 别以 G1 ( s ), G 2 ( s ), L , G n ( s ) 表示,则有
基本规律:设
G ( s) =
K (τ 1 s + 1) L (τ m s + 1) sν (T1 s + 1) L (Tu s + 1)
(1)
(2) m < n
ω → 0+ ω →0
K ν n = ν + u ω → ∞ ∠G ( j∞) = ( m − n) × 90 o
3型
(3)幅相曲线与实轴、虚轴的交点求取。 (4) 不包含一阶微分环节, 包含一阶微分环节的幅相曲线。
j ( − − arc tgωT ) 2
π
P
A θ
jω
α 0
−1 / T
概略地绘制开环幅相曲线应当反映开环频率特性的三个重要因素: (1)开环幅相曲线的起点 ω =0 + 与终点 ω = ∞ (2)开环幅相曲线与实轴、虚轴的交点 (3)开环幅相曲线的变化范围(象限、单调性)
2012-4-26 Automatic Control Theory 2
2 2 2
2012-4-26 Automatic Control Theory 4
Q G ( j 0) = K∠0 o , G ( j∞) = 0∠ − 180 o
起点: 起点: G ( j 0 ) = A ( 0 ) = K 终点: G ( j ∞ ) = A ( ∞ ) = 0 终点: 与实轴的交点: 与实轴的交点: Q (ω x ) = 0
由于含有两个惯性环节,当 ω → ∞ 由此可见,若包含 n 个惯性环节,则有
G ( jω ) → 0∠ − 180 o
ω → ∞ G ( jω ) → 0∠ − n × 90 o
2012-4-26 Automatic Control Theory 6
由此可见,若包含 n 个惯性环节, ω → ∞ m个一阶微分环节,则有
∠G( j0) = ϕ(0) = 0o ∠G( j∞) = ϕ(∞) = −180o
Q Q (ω ) = − K (T1 + T2 )ω /(1 + T12ω 2 )(1 + T2 2ω 2 ) = 0
与虚轴的交点: 与虚轴的交点: P (ω y ) = 0
ωx = 0
P (ω ) = K (1 − T1T2ω 2 ) /(1 + T1 2ω 2 )(1 + T2 2ω 2 )
2型
j Im
0
0型
Re
2012-4-26
Automatic Control Theory
1型
12
例4 设系统开环传递函数为
G (s) H (s) = K
2 s (Ts + 1)[( s 2 / ω n ) + 1]
K, T > 0
