绘制下列传递函数的幅相曲线：

合集下载

自动控制原理及应用各章习题清华董红生

习题1-1 什么是自动控制？什么是自动控制系统？1-2 试比较开环控制和闭环控制的优缺点。

1-3 自动控制系统有哪些基本组成元件？这些元件的功能是什么？1-4 简述反馈控制系统的基本原理。

1-5 简述对自动控制系统基本要求。

1-6 试举几个日常生活中的开环和闭环控制系统的实例，并说明它们的工作原理。

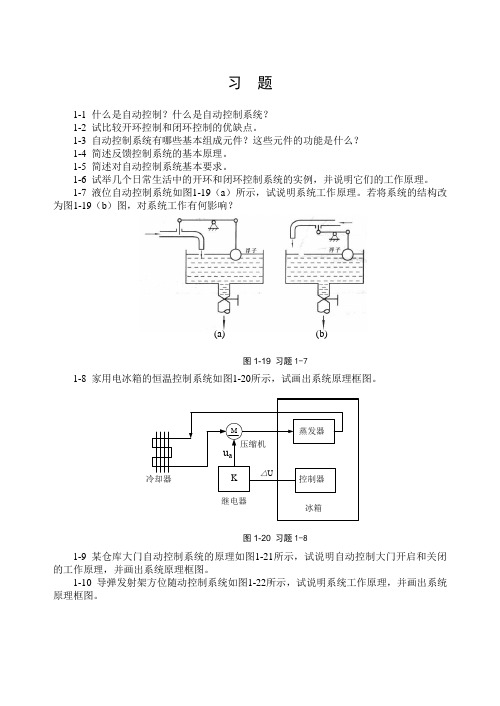
1-7 液位自动控制系统如图1-19（a）所示，试说明系统工作原理。

若将系统的结构改为图1-19（b）图，对系统工作有何影响？(a) (b)图1-19习题1-71-8 家用电冰箱的恒温控制系统如图1-20所示，试画出系统原理框图。

图1-20习题1-81-9 某仓库大门自动控制系统的原理如图1-21所示，试说明自动控制大门开启和关闭的工作原理，并画出系统原理框图。

1-10 导弹发射架方位随动控制系统如图1-22所示，试说明系统工作原理，并画出系统原理框图。

图1-20 习题1-8nU fU cU aU rθ图1-21 习题1-10习题2-1 试建立如图2-39所示电路的微分方程。

1R )C（b ）（a ）图2-39 习题2-12-2求下列函数的拉普拉斯逆变换。

（1）)3)(2(1)(+++=s s s s F（2）)3()2(1)(3++=s s s s F （3）)22(1)(2+++=s s s s s F2-3设系统传递函数为)2)(1(2)()(++=s s s R s C ，初始条件1)0(-=c ，0)0(=∙c ，试求单位阶跃信号作用时，系统输出响应)(t c 。

2-4若某系统在单位阶跃输入信号时，零初始条件下的输出响应t t e e t c --+-=21)(，试求系统的传递函数。

2-5使用复阻抗法写出如图2-40所示有源电路的传递函数。

)1C图2-40 习题2-52-6 已知系统方程组如下：⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X 试绘制系统结构图，并求闭环传递函数)()(s R s C 。

(完整版)自动控制原理课后习题及答案

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(1) 优点:结构简单，成本低，工作稳定。

用于系统输入信号及扰动作用能预先知道时，可得到满意的效果。

(2) 缺点：不能自动调节被控量的偏差。

因此系统元器件参数变化，外来未知扰动存在时，控制精度差。

2 闭环系统⑴优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值，都会产生控制作用去清除此偏差，所以控制精度较高。

它是一种按偏差调节的控制系统。

在实际中应用广泛。

⑵缺点：主要缺点是被控量可能出现波动，严重时系统无法工作。

1-2 什么叫反馈？为什么闭环控制系统常采用负反馈？试举例说明之。

解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。

闭环控制系统常采用负反馈。

由1-1中的描述的闭环系统的优点所证明。

例如，一个温度控制系统通过热电阻（或热电偶）检测出当前炉子的温度，再与温度值相比较，去控制加热系统，以达到设定值。

1-3 试判断下列微分方程所描述的系统属于何种类型（线性，非线性，定常，时变）？（1）22()()()234()56()d y t dy t du t y t u t dt dt dt ++=+（2）()2()y t u t =+（3）()()2()4()dy t du t ty t u t dt dt +=+ （4）()2()()sin dy t y t u t tdt ω+=（5）22()()()2()3()d y t dy t y t y t u t dt dt ++= （6）2()()2()dy t y t u t dt +=（7）()()2()35()du t y t u t u t dt dt =++⎰解答：（1）线性定常（2）非线性定常（3）线性时变（4）线性时变（5）非线性定常（6）非线性定常（7）线性定常1-4 如图1-4是水位自动控制系统的示意图，图中Q1，Q2分别为进水流量和出水流量。

自动控制原理试-4

自动控制原理试-4(总分：100.00，做题时间：90分钟)一、(总题数：29，分数：100.00)1.已知某系统结构图如图所示，试根据频率特性物理意义，求当信号输入为r(t)=2sin(t+30°)+cos(2t-45°)时，系统的稳态输出c ss和稳态误差e ss。

（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：闭环传递函数；频率特性；；误差传递函数；误差频率特性；；当r 1(t)=2sin(t+30°)时，当r 2 (t)=cos(2t-45°)时，因此在输入作用下，2.最小相位系统对数幅频渐近特性如图所示，请确定系统的传递函数。

（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：由图知在低频段渐近线斜率为0，因为最小交接频率前的低频段L(ω)=-v20lgω，故v=0。

渐近特性为分段线性函数，在各交接频率处，渐近特性斜率发生变化。

在ω=0.1处斜率变化20dB/dec，属一阶微分环节。

在ω=ω1处斜率变化-20dB/dec，属惯性环节。

在ω=ω2处斜率变化-20dB/dec，属惯性环节。

在ω=ω3处斜率变化-20dB/dec，属惯性环节。

在ω=ω4处斜率变化-20dB/dec，属惯性环节。

因此，系统的传递函数具有下述形式式中，K，ω1，ω2，ω3，ω4待定。

由201gK=30得K=10 1.5≈31.62。

因渐近线直线段，若设某段的斜率为k，(ωA，L(ωA ))，(ωB，L(ωB ))为该线段上的两点，则由直线方程：确定所以确定，所以确定，所以确定，所以于是，所求的传递函数为单位反馈控制系统的开环传递函数为：（分数：4.00）(1).求系统的幅值裕量为20dB时的K值。

自控试题练习题集

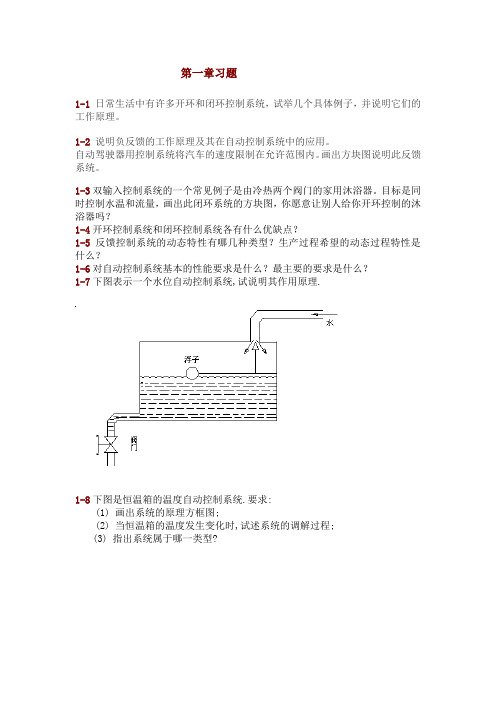
第一章习题1-1日常生活中有许多开环和闭环控制系统，试举几个具体例子，并说明它们的工作原理。

1-2说明负反馈的工作原理及其在自动控制系统中的应用。

自动驾驶器用控制系统将汽车的速度限制在允许范围内。

画出方块图说明此反馈系统。

1-3双输入控制系统的一个常见例子是由冷热两个阀门的家用沐浴器。

目标是同时控制水温和流量，画出此闭环系统的方块图，你愿意让别人给你开环控制的沐浴器吗？1-4开环控制系统和闭环控制系统各有什么优缺点？1-5反馈控制系统的动态特性有哪几种类型？生产过程希望的动态过程特性是什么？1-6对自动控制系统基本的性能要求是什么？最主要的要求是什么？1-7下图表示一个水位自动控制系统,试说明其作用原理.1-8下图是恒温箱的温度自动控制系统.要求:(1) 画出系统的原理方框图;(2) 当恒温箱的温度发生变化时,试述系统的调解过程;(3) 指出系统属于哪一类型?1-9 下图为位置随动系统,输入量为转角r θ,输出量为转角c θ,p R 为圆盘式滑动电位器,s K 为功率放大器SM 为伺服电动机.要求: (1)说明系统由哪几部分组成,各起什么作用？ (2)画出系统原理方框图;(3)说明当r θ 变化时, c θ的跟随过程.1-10 位置随动系统如下图所示,回答以下问题 1.说明该系统的以下(1)-(10)各是什么:(1)被控制对象 (2)被控制量 (3)给定元件 (4)给定量 (5)主反馈元件 (6)主反馈量 (7)误差量 (8)负载 (9)积分元件 (10)执行元件. 2.画出系统作用方框图,表出个环节的输入输出量。

3.判断(在括号内对的上面打"对号")(1)该系统是(按偏差;按扰动)原则的控制系统; (2)该系统是(有差;无差)系统; (3)该系统是(0型,1型,2型)系统; (4)该系统的输入量是(rr U Q 、);(5)该系统的输出量是(c c U Q 、)。

1－11下图为温度自动控制系统,改变a 点位置可以改变恒温温度.试说明该系统的工作原理和性能,并指出它属何种类型?1-12如题图（a ）、（b ）所示两水位控制系统，要求∙ 画出方块图（包括给定输入量和扰动输入量）； ∙ 分析工作原理，讨论误差和扰动的关系。

自动控制理论第五章习题汇总

自动控制理论第五章习题汇总填空题1、系统的频率响应与正弦输入信号之间的关系称为频率响应2、在正弦输入信号的作用下，系统输入的稳态分量称为频率响应简答题：5-2、什么是最小相位系统及非最小相位系统？最小相位系统的主要特点是什么？答在s平面上，开环零、极点均为负实部的系统称为最小相位系统；反之，开环零点或极点中具有正实部的系统称为非最小相位系统。

最小相位系统的主要特点是：相位滞后最小，并且幅频特性与相频特性有惟一的确定关系。

如果知道最小相位系统的幅频特性，可惟一地确定系统的开环传递函数。

5-3、什么是系统的频率响应？什么是幅频特性？什么是相频特性？什么是频率特性？答对于稳定的线性系统，当输入信号为正弦信号时，系统的稳态输出仍为同频率的正弦信号，只是幅值和相位发生了改变，如图5-3所示，称这种过程为系统的频率响应。

图5-3称为系统的幅频特性，它是频率的函数；称为系统的相频特性，它是频率的函数：称为系统的频率特性。

稳定系统的频率特性可通过实验的方法确定。

计算题5-1、设某控制系统的开环传递函数为)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图，并确定剪切频率c ω的值。

解：Bode 图如下所示剪切频率为s rad c /75.0=ω。

5-2、某系统的结构图和Nyquist 图如图(a)和(b)所示，图中2)1(1)(+=s s s G 23)1()(+=s s s H 试判断闭环系统稳定性，并决定闭环特征方程正实部根的个数。

解：由系统方框图求得内环传递函数为：ss s s s s s H s G s G +++++=+23452474)1()()(1)( 内环的特征方程：04742345=++++s s s s s由Routh 稳定判据：1:0310:16:44:171:01234s s s s s由此可知，本系统开环传函在S 平面的右半部无开环极点，即P=0。

自动控制原理卢京潮主编课后习题答案西北工业大学出版社

自动控制原理卢京潮主编课后习题答案西北工业大学出版社SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第五章线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。

(a) (b)图5-75 R-C 网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s（1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r 解系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ （2）当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应试求系统频率特性。

开环幅相曲线绘制

（3）在交接频率处，曲线斜率发生改变，改变的多少取决于典型环节的类型。
2 1 T1 2 2 1 T2 2 2 ( ) 180 arctgT 1 arctgT 2
2019/3/29 Automatic Control Theory

K
e j ( )
10
j Im
起点与终点：
0
Re 0
G( j 0 ) 180o , G( j) 0 360o
0
2019/3/29
P(0 ) V x K (T1 T2 T3 )
Automatic Control Theory 9
令
Q( ) 0 , x 1 / T1T2 T2T3 T3T1
K (T1 T2 T3 ) x 2T1T2T3
K K
, 1 / s , 1 /(Ts 1) , 1 / j , 1 /( jT 1)
绘制典型环节Bode图的数据： 20 log K 20 log7 16.9 (dB)
转折频率
2019/3/29
1 / T 1 / 0.087 11.5 (rad / s)
16
Automatic Control Theory
在 n 附近,相角突变
-180o，幅相曲线在 n 处出现了不连续

n
0

n
2019/3/29
Automatic Control Theory
14
4、开环对数频率特性曲线的绘制设传递函数 G ( s) 由n个典型环节串联组成，n个典型积分环节分别以 G1 ( s), G 2 ( s), , G n ( s) 表示，则有

开环幅相曲线绘制

2 / n 1 / 2 , n 2 , 0.3535 0.35
13
1
注意开环传递函数含有一个等幅振荡环节
(s
2
/

2 n
)

1
当 n A(n ) | G( jn )H( jn ) |
(n ) 90o tg 1Tn 180o ; n n , 0
(n ) 90o tg 1Tn 180o ; n n , 0

KT
j
K
(1 T 2 2 )[1 ( 2 / n2 )] (1 T 2 2 )[1 ( 2 / n2 )]
起点: G( j0 )H ( j0 ) 90o 终点: G( j)H ( j) 0360o
2019/12/19
Automatic Control Theory
12
例4 设系统开环传递函数为
G(s)H (s)
K
s(Ts 1)[(s2 / n2 ) 1]
K, T 0
试绘制系统的开环概略的幅相曲线。
解:
G( j)H ( j)
K
j( jT 1)[1 ( 2 / n2 )]

K (T j)
(1 T 2 2 )[1 ( 2 / n2 )]
0
（1） 0
K

（2） m n n u G( j) (m n) 90o
（3）幅相曲线与实轴、虚轴的交点求取。
（4）不包含一阶微分环节，
3型
j Im
包含一阶微分环节的幅相曲线。
2型
0
Re
0型
2019/12/19
Automatic Control Theory 1型

《自动控制原理》答案李红星第五章

由上式可得
0<K <
3 2
b 、 K = 10 时，对于开环幅相曲线与实轴的交点有
Kω (T ω 2 − 1) 10ω (T ω 2 − 1) = =0 (T + 1)2 ω 4 + ω 2 (T ω 2 − 1)2 (T + 1)2 ω 4 + ω 2 (T ω 2 − 1)2
由上式可得 ω =
1 ，则交点的实轴坐标为 T
− K (τ j∞ + 1) = 0, ϕ (∞) = −180o ∞ 2 (Tj∞ + 1)
又由于 G ( jω ) H ( jω ) =
− K (τ jω + 1) − K (τ T ω 2 + 1) + jK ω (T − τ ) = ，所以有 ω 2 (Tjω + 1) ω 2 (T 2ω 2 + 1)
要求画出以下 4 种情况下的奈奎斯特曲线，并判断闭环系统的稳定性： a． T2 = 0 ；
141
b． 0 < T2 < T1 ； c． 0 < T2 = T1 ； d． 0 < T1 < T2 。解： a．当 T2 = 0 时， Q ( s ) =
K ， s (T1 s + 1)
2
其开环幅相曲线如题 5-5 解图 a 所示， P = 0 ，N=2 则 Z=P+N=2，故在 s 平面右半平面有 2 个闭环极点，闭环系统不稳定； b．当 0 < T2 < T1 时， Q( jω ) =
a 、 T = 2 时，对于开环幅相曲线与实轴的交点有
K ω (T ω 2 − 1) K ω (2ω 2 − 1) = =0 (T + 1) 2 ω 4 + ω 2 (T ω 2 − 1)2 9ω 4 + ω 2 (2ω 2 − 1) 2

自动控制原理复习题(二)

自动控制原理复习题（二）一、选择题1、下列串联校正装置的传递函数中，能在1c ω=处提供最大相位超前角的是：A. 1011s s ++C. 210.51s s ++B. 1010.11s s ++ D. 0.11101s s ++2、一阶系统的闭环极点越靠近S 平面原点：A. 准确度越高 C. 响应速度越快B. 准确度越低 D. 响应速度越慢3、已知系统的传递函数为1s Ke TS τ-+，其幅频特性()G j ω应为： A. 1Ke T τω-+τω-B. 1Ke T τωω-+4、梅逊公式主要用来（）A. 判断稳定性 C. 求系统的传递函数B. 计算输入误差 D. 求系统的根轨迹5、适合应用传递函数描述的系统是： A. 单输入，单输出的线性定常系统；B. 单输入，单输出的线性时变系统；C. 单输入，单输出的定常系统；D. 非线性系统。

6、对于代表两个或两个以上输入信号进行（）的元件又称比较器。

A. 微分 C. 加减B. 相乘 D. 相除 7、直接对控制对象进行操作的元件称为（）A. 比较元件C. 执行元件B.给定元件D. 放大元件8、二阶欠阻尼系统的性能指标中只与阻尼比有关的是（）A. 上升时间C. 调整时间B.峰值时间D. 最大超调量9、在用实验法求取系统的幅频特性时，一般是通过改变输入信号的（）来求得输出信号的幅值。

A. 相位C. 稳定裕量B.频率D. 时间常数10、已知二阶系统单位阶跃响应曲线呈现出等幅振荡，则其阻尼比可能为（）A. 0.707 C. 1B.0.6 D. 011、非单位反馈系统，其前向通道传递函数为G(S)，反馈通道传递函数为H(S)，则输入端定义的误差E(S)与输出端定义的误差*()E S之间有如下关系：A.* ()()() E S H S E S=⋅C.*()()()()E S G S H S E S=⋅⋅B.*()()()E S H S E S=⋅D.*()()()()E S G S H S E S=⋅⋅12、若两个系统的根轨迹相同，则有相同的：A. 闭环零点和极点C. 闭环极点B.开环零点D. 阶跃响应13、已知下列负反馈系统的开环传递函数，应画零度根轨迹的是：A.*(2) (1) K s s s-+C.*2(31)Ks s s+－B.*(1)(5Ks s s-+）D.*(1)(2)K ss s--14、闭环系统的动态性能主要取决于开环对数幅频特性的：A. 低频段C. 高频段B.开环增益D. 中频段15、系统特征方程式的所有根均在根平面的左半部分是系统稳定的（）A. 充分条件C. 充分必要条件B.必要条件D. 以上都不是16、以下关于系统稳态误差的概念正确的是（ C ）A. 它只决定于系统的结构和参数B.它只决定于系统的输入和干扰C. 与系统的结构和参数、输入和干扰有关D. 它始终为0非线性系统17、当输入为单位加速度且系统为单位反馈时，对于I型系统其稳态误差为（）A. 0 C. 1/kB.0.1/k D.18、开环控制的特征是（）A. 系统无执行环节C. 系统无反馈环节B.系统无给定环节D. 系统无放大环节19、若已知某串联校正装置的传递函数为，则它是一种（）A. 相位滞后校正C. 微分调节器B.相位超前校正D. 积分调节器20、在信号流图中，只有（）不用节点表示。

第5章2——Nyquist曲线

11
2 n arc tg n 2 1 2 n 2 n arc tg n 2 1 2 n
2016/5/20
autocumt@
5-2 幅相频率特性——Nyquist曲线
d A( ) 0 d d 1 0 d 2 2 2 2 1 n n
S (T j S 1)
j 1
h
1 ( n h ) 2 j 1
2 2 ( T j S 2 jT j S 1)
开环传递函数分解成典型环节串连形式
autocumt@ 1
G( S ) H ( S ) Gi ( S )
i 1
N
5-2 幅相频率特性——Nyquist曲线
谐振频率：r n 1 2 2 谐振峰值：M r 1 2 1
2
自动控制原理
Im 0
0 1 Re

1 2
n
M
r

A ( r )
r
2 谐振条件： 0 0.707 2
autocumt@ 12
振荡环节的幅相特性曲线
2016/5/20
A( ) 1 T 1
2 2
( ) arctan T
Im
A(0) 1; (0) 0 A() 0; () 90
0 45
1 0
Re

autocumt@ 6
1 T
2016/5/20
5-2 幅相频率特性——Nyquist曲线
i 1
结论：开环幅频特性是串联环节幅频特性幅值之积开环相频特性是串联环节相频特性相角之和
autocumt@

自动控制原理第五章课后答案

五频域分析法2-5-1 系统单位阶跃输入下的输出)0(8.08.11)(94≥+-=--t e e t c tt ,求系统的频率特性表达式。

【解】： 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G2-5-2系统时，系统的稳态输出（1）)30sin()(0+=t t r ；（2）)452cos(2)(0+=t t r ；（3）)452cos(2)30sin()(00--+=t t t r 。

【解】：求系统闭环传递函数5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义，以及线性系统的迭加性求解如下：（1）︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ（2）︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s（3）)8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s2-5-3 试求图2-5-3所示网络的频率特性，并绘制其幅相频率特性曲线。

【解】：（1）网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R C j R j G（2）绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j eT T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。

《自动控制原理(第二版)》课后答案(卢京潮著)西北工业大学出版社_1-185

第一章自动控制的一般概念习题及答案1-1 根据题1-15图所示的电动机速度控制系统工作原理图，完成：(1)将a，b与c，d用线连接成负反馈状态；(2)画出系统方框图。

解（1）负反馈连接方式为：a↔d，b↔c；（2）系统方框图如图解1-1所示。

1-2 题1-16图是仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开、闭的工作原理，并画出系统方框图。

图1-16仓库大门自动开闭控制系统1解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如图解1-2所示。

1-3 图1-17为工业炉温自动控制系统的工作原理图。

分析系统的工作原理，指出被控对象、被控量和给定量，画出系统方框图。

图1-17 炉温自动控制系统原理图解加热炉采用电加热方式运行，加热器所产生的热量与调压器电压u c的平方成正比，u c 增高，炉温就上升，u c的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压u f。

u f作为系统的反馈电压与给定电压u r进行比较，得出偏差电压u e，经电压放大器、功率放大器放大成u a后，作为控制电动机的电枢电压。

在正常情况下，炉温等于某个期望值T°C，热电偶的输出电压u f正好等于给定电压u r。

此时，u e=u r−u f=0，故u1=u a=0，可逆电动机不转动，调压器的滑动触点停留在某个合适的位置上，使u c保持一定的数值。

这时，炉子散失的热量正好等于从加热器吸取的热量，形成稳定的热平衡状态，温度保持恒定。

当炉膛温度T°C由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下2的控制过程：控制的结果是使炉膛温度回升，直至T°C的实际值等于期望值为止。

绘制下列传递函数的幅相曲线：

习题5-1 试求图5-76(a)、(b) 所示网络的频率特性。

图5-76 R-C 网络5-2 某系统结构图如图5-77所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s(1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 5-3 若系统单位阶跃响应h t e e t t t()..=-+≥--11808049试求系统频率特性。

5-4 绘制下列传递函数的幅相曲线： ()()/1G s K s = ()()/22G s K s = ()()/33G s K s =5-5 已知系统开环传递函数 )15.0)(12(10)()(2+++=s s s s s H s G试分别计算当5.0=ω 和2=ω 时开环频率特性的幅值)(ωA 和相角)(ωϕ。

5-6 试绘制下列传递函数的幅相特性曲线。

(1) G s s s ()()()=++52181(2) G s s s ()()=+10125-7 已知系统开环传递函数 )1()1()(12++-=s T s s T K s G ； 12(,,0)K T T >当1=ω时，()180G j ω∠=-︒，5.0)(=ωj G ；当输入为单位速度信号时，系统的稳态误差为 1，试写出系统开环频率特性表达式)(ωj G 。

5-8 已知系统开环传递函数 )1)(1(10)(2++=s s s s G 试概略绘制系统开环幅相曲线。

5-9 绘制下列传递函数的渐近对数幅频特性曲线。

(1) G s s s ()()()=++22181(2) G s s s s ()()()=++20011012(3) G s s s s s s ()(.)(.)()=++++40050212(4) G s s s s s s s ()()()()()=+++++20316142510122(5)G s s s s s s s ()(.)()()=+++++8011425225-10 若传递函数 G s KsG s v ()()=0 式中，)(0s G 为)(s G 中，除比例和积分两种环节外的部分，试证ω11=K v式中，1ω为近似对数幅频特性曲线最左端直线（或其延长线）与零分贝线交点的频率，如图5-78所示。

自动控制原理复习题(二)

6、对于代表两个或两个以上输入信号进行（）的元件又称比较器。

自控习题

1-1 下图是仓库大门自动控制系统原理示意图，试说明系统自动控制大门开、闭的工作原理，并画出系统方框图。

1-2 根据图所示的电动机速度控制系统工作原理图，完成：(1) 将a ，b 与c ，d 用线连接成负反馈状态； (2) 画出系统方框图。

1-3 图 (a)，(b)所示的系统均为电压调节系统。

假设空载时两系统发电机端电压均为110V ，试问带上负载后，图(a)，(b)中哪个能保持110V 不变，哪个电压会低于110V ？为什么?2-1 试建立下图所示各系统的微分方程。

其中电压)(t u r 和位移)(t x 为输入量；电压)(t u c 和位移)(t y 为输出量；R （电阻），C （电容），k （弹性系数），和f （阻尼系数），均为常数。

2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

2-3 求下图所示各有源网络的传递函数)()(s U s U r c 。

2-4 已知在零初始条件下，系统的单位阶跃响应为 t te et c --+-=221)(，试求系统的单位脉冲响应和传递函数。

2-5 系统传递函数 232)()(2++=s s s R s C ，试求初始条件为1)0(c -=、0)0(c = 时系统在输入信号)t (1)t (r =作用下的输出)t (c 。

2-6 飞机俯仰角控制系统结构图如图所示，试求闭环传递函数)()(s s Q r c 。

2-7 已知系统方程组如下，试绘制系统结构图，并求闭环传递函数)()(s R s C 。

⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X2-8 试用结构图等效变换法化简下图所示系统，并求各系统的传递函数)()(s R s C 。

自动控制原理习题

（1）；
（2）；
试确定它们的开环传递函数。
5－4如下10个控制系统的开环传递函数分别为
（1）；
（2）
（3）
（4）
（5）
（6）
（7）
（8）
（9）
（10）
适当选择各题正值参数有题5－4图中顺序对应题号的开环幅相频率特性，试判断它们的稳定性。
5－5某控制系统的动态结构图如题5－5图所示，试绘制该系统的开环幅相频率特性，并判别系统的稳定性。如果系统不稳定，有几个不稳定的闭环极点？
6－3题6－3图所示三个控制系统的开环对数幅频特性渐近线和串联校正环节的对数幅频特性渐近线均已知。试写出它们校正后的开环传递函数表达式，并计算图a、图b所示两系统校正后的相位裕度和幅频裕度，时域指标的超调量和调节时间。
6－4 一单位负反馈控制系统的开环传递函数为
(1) 试设计串联超前校正装置的传递函数，使系统在不改变稳态传输的前提下具有的相位裕度和13～16dB的幅值裕度，并估算校正后系统响应的最大超调量和调节时间；
校正后要求稳态误差系数，试分别设计串联校正装置的传递函数,满足：
（1）系统开环频域指标，；
（2）系统闭环频域指标，。
6－7 某晶闸管整流的直流电动机速度给定控制系统是由电流内环和转速外环组成的。其中电流内环的系统动态结构图如题6－7图所示。其中，为电流给定量滤波环节的传递函数；为晶闸管整流环节的传递函数；为直流电动机环节的传递函数；为电流检测信号经滤波环节的传递函数。试按典Ⅰ期望特性设计电流环调节器的传递函数，使：
3－15若某单位负反馈控制系统的闭环传递函数有如下的形式
试计算给定输入量时系统的稳态误差。
3－16某系统动态结构图如题3－16图所示。其中增益值、和时间常数、均为正数，试计算在给定输入量，扰动输入量共同作用时响应的稳态误差。

自动控制原理(第2版)(余成波)_第5章习题解答 -

108第5章频率特性法教材习题同步解析5.1 一放大器的传递函数为：G (s )=1+Ts K测得其频率响应，当ω=1rad/s 时，稳态输出与输入信号的幅值比为12/2，稳态输出与输入信号的相位差为－π/4。

求放大系数K 及时间常数T 。

解：系统稳态输出与输入信号的幅值比为A ==222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ϕω=-=-︒，即1T ω=当ω=1rad/s 时，联立以上方程得T =1，K =12放大器的传递函数为：G (s )=121s +5.2 已知单位负反馈系统的开环传递函数为5()1K G s s =+ 根据频率特性的物理意义，求闭环输入信号分别为以下信号时闭环系统的稳态输出。

（1）r （t ）=sin （t +30°）；（2）r （t ）=2cos （2t －45°）；（3）r （t ）= sin （t +15°）－2cos （2t －45°）；解：该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为109365)(2+=ωωA闭环系统的相频特性为6arctan )(ωωϕ-=（1）输入信号的频率为1ω=，因此有37375)(=ωA ，()9.46ϕω︒=- 系统的稳态输出()20.54)37ss c t t ︒=+ （2）输入信号的频率为2ω=，因此有()A ω=，()18.43ϕω︒=- 系统的稳态输出()cos(263.43)2ss c t t ︒=- （3）由题（1）和题（2）有对于输入分量1：sin （t +15°），系统的稳态输出如下1() 5.54)37ss c t t ︒=+ 对于输入分量2：－2cos （2t －45°），系统的稳态输出为2()63.43)ss c t t ︒=- 根据线性系统的叠加定理，系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(︒︒--+=t t t c ss5.3 绘出下列各传递函数对应的幅相频率特性与对数频率特性。

1-5-1绘制下列传递函数的对数幅频渐进特性曲线：

1-5-1 绘制下列传递函数的对数幅频渐进特性曲线：（1）)18)(12(2)(++=s s s G ；解：①确定各交接频率ωi ，i ＝1,2。

惯性环节：ω1＝1/2 －20db/dec 惯性环节：ω2＝1/8 －20db/dec 最小交接频率：ωmin ＝ω2＝1/8②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝0∴低频渐进斜率k ＝0db/dec又Q La(0.1)＝20lg2－20*0*lg0.1＝6.02db ∴曲线过（0.1，6.02）点③绘制频段（ω≥ωmin ）渐进特性曲线。

ωmin ≤ω＜ω1 k ＝－20db/decω≥ω1 k ＝－40db/dec ④系统开环对数幅频渐进特性曲线如下图：（2）)110)(1(200)(2++=s s s s G ；解：①确定各交接频率ωi ，i ＝1,2。

惯性环节：ω1＝1 －20db/dec惯性环节：ω2＝0.1 －20db/dec 最小交接频率：ωmin ＝ω2＝0.1②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝2∴低频渐进斜率k ＝－40db/dec又Q La(1)＝20lg200－20*2*lg1＝20lg200＝46.02db∴曲线过（1，46.02）点③绘制频段（ω≥ωmin ）渐进特性曲线。

ωmin ≤ω＜ω1 k ＝－60db/decω≥ω1 k ＝－80db/dec ④系统开环对数幅频渐进特性曲线如下图：（3）)12)(1()11.0(8)(2++++=s s s s ss G ；解：①确定各交接频率ωi ，i ＝1,2,3。

一阶微分环节：ω1＝0.1 20db/dec惯性环节： ω2＝2 －20db/dec 振荡环节： ω3＝1 －40db/dec最小交接频率：ωmin ＝ω1＝0.1②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝1∴低频渐进斜率k ＝－20db/dec又Q La(1)＝20lg8－0＝20lg8＝18.06db∴曲线过（1，18.06）点③绘制频段（ω≥ωmin ）渐进特性曲线。

控制习题

1-1 试比较开环控制系统和闭环控制系统的优缺点。

1-2 试列举几个日常生活中的开环和闭环控制系统的例子，并说明其工作原理。

1-3 图1-8是水位控制系统的示意图，图中1Q ,2Q 分别为进水流量和出水流量。

控制的目的是保持水位为一定的高度。

试说明该系统的工作原理并画出其方框图。

1-4 仓库大门自动控制系统如图1-9所示，试分析系统的工作原理，绘制系统的方框图，指出各实际元件的功能及输入、输出量。

1-5 瓦特发明的蒸汽机机械式离心调速器，被认为是近代早期典型的自动调节装置，系统示意图如图1-10所示，试说明该系统的工作原理并画出其方框图。

1-6 图1-11所示为角位置随动系统工作原理图，简述其工作原理并画出系统方框图。

习题33-1 某一系统的数学模型为y=x 2。

试求其线性化方程。

求当x 在10附近时的线性化方程，并求将此线性化方程用于x=11时y 的误差。

3-2 图3-40是一旋转运动的惯量-阻尼-弹簧系统物理模型。

若输入量为转矩T ，输出量为转子转角θ，求传递函数，并写成式（3-28）的形式，求无阻尼固有频率ωn 及阻尼比ζ。

3-3 求图3-41所示二系统的传递函数。

3-4 证明图3-42中机械系统与电气系统是相似系统，即证明两者传递函数具有相同的形式。

3-5 试分析当反馈环节H(s)=1时，前向通道传递函数G(s)分别为惯性环节、微分环节、积分环节时，系统闭环传递函数为什么？3-6 化简图3-43的方框图，并求系统传递函数。

3-7 化简图3-44的方框图，并求系MθJck图3-40 题3-2图x i (t)x 0(t)mc ku i (t)u o (t)CR L（a ）（b ）图3-41 题3-3图（a ）（b ）x i (t)x 0(t)c 1k 2c 2k 1u i (t)u o (t)C 1R 1C 2R 2图3-42 题3-4图统传递函数。

3-8 化简图3-45的方框图，并求系统传递函数。

绘制下列传递函数的幅相曲线：

自动控制原理及应用各章习题清华董红生

(完整版)自动控制原理课后习题及答案

自动控制原理试-4

自控试题练习题集

自动控制理论第五章习题汇总

自动控制原理卢京潮主编课后习题答案西北工业大学出版社

开环幅相曲线绘制

开环幅相曲线绘制

《自动控制原理》答案 李红星 第五章

自动控制原理复习题(二)

第5章2——Nyquist曲线

自动控制原理第五章课后答案

《自动控制原理(第二版)》课后答案(卢京潮著)西北工业大学出版社_1-185

绘制下列传递函数的幅相曲线：

自动控制原理复习题(二)

自控习题

自动控制原理习题

自动控制原理(第2版)(余成波)_第5章习题解答 -

1-5-1绘制下列传递函数的对数幅频渐进特性曲线：

控制习题

《自动控制原理》答案李红星第五章