速度投影
合集下载
平面图形上加速度投影定理的数学证明
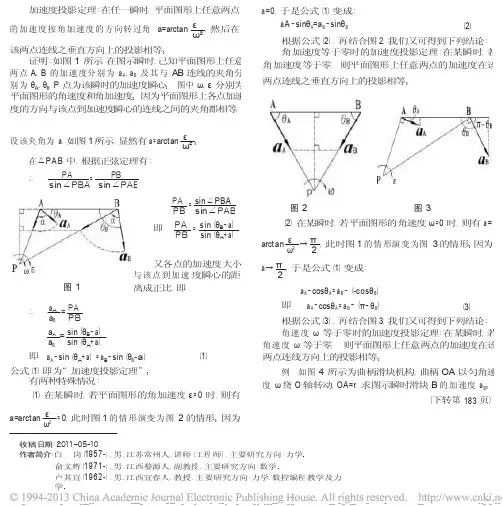
加速度投影定理：在任一瞬时，平面图形上任意两点a=0，于是公式（1）变成：a A·sinθA=a B·sinθB的加速度按角加速度的方向转过角a=arctan ε ，然后在（2）ω2根据公式（2），再结合图2，我们又可得到下列结论：角加速度等于零时的加速度投影定理：在某瞬时，若角加速度等于零，则平面图形上任意两点的加速度在该两点连线之垂直方向上的投影相等。
该两点连线之垂直方向上的投影相等。
证明：如图1 所示，在图示瞬时，已知平面图形上任意两点A、B的加速度分别为a A、a B及其与AB 连线的夹角分别为θA、θB，P点为该瞬时的加速度瞬心。
图中ω、ε分别为平面图形的角速度和角加速度。
因为平面图形上各点加速度的方向与该点到加速度瞬心的连线之间的夹角都相等，设该夹角为a，如图1 所示，显然有a＝arctanε 。
ω2在△PA B 中，根据正弦定理有：PA＝PB∴sin∠PBA sin∠PABP A＝s in∠PBA图2图3PB sin∠PAB（2）在某瞬时，若平面图形的角速度ω＝0时，则有a=P A＝sin（θB－a）即PB sin（θA＋a）arctan ε →π，此时图1 的情形演变为图3 的情形。
因为ω22又各点的加速度大小与该点到加速度瞬心的距离成正比，即a→π，于是公式（1）变成：2图1aA·cosθA＝a B·（-cosθB）a A·cosθA＝a B·（π－θB）即（3）a A=P A∴a B PB根据公式（3），再结合图3，我们又可得到下列结论：角速度ω等于零时的加速度投影定理：在某瞬时，若角速度ω等于零，则平面图形上任意两点的加速度在该两点连线方向上的投影相等。
例如图4 所示为曲柄滑块机构，曲柄OA 以匀角速度ω绕O 轴转动，OA=r，求图示瞬时滑块B 的加速度a B。
（下转第183 页）a A = sin（θB－a）a B sin（θA＋a）a A·sin（θA＋a）＝a B·sin（θB-a）即（1）公式（1）即为“加速度投影定理”。
理论力学(武清玺,高教版)课后习题解答(6)
再以B为基点, 求 a c
ac = aB + aCB + aCB
τ
n
(b)
作加速度矢量图，P2 为BC的瞬心，而 P2C = 9 r
∴ ω BC =
vc 3 1 ωo = rω o ⋅ = P2 C 2 9r 6
2
aCB = BC ⋅ ω BC = 3 3r ⋅ (
n
ωo
6
)2 =
3 2 rω o 12
n
将 (b) 式在BC方向线上投影： ac = a B cos 30o − aCB =
r 2 3 3 3 2 2 ωo ⋅ − rω o = rω o 3 2 12 12
8-23 解： （1） v A = OA ⋅ ω AB 杆的速度瞬心为 O， 所以 AB 的角速度为ω， 因此： v B = OB ⋅ ω = 200 × 2 = 400 mm/s ω vA
由于 aa = ae + ae + ar + ar + aC
n n
va
M
v r = rw2 = 100 × 6 = 600(mm/s)
ω2
r O
vr
ω1
α1
arτ arn
A O
τ
τ
a
n e
aC
M
ae = 3rα1 = 3 × 100 × 3 = 900mm/s ar = rα 2 = 100 × 4 = 400mm/s
y
vD D
Q v A cos ϕ = v B = OB ⋅ ω ∴ ω AD OB ⋅ w v OB ⋅ ω cos ϕ = A = = PA PA PA ⋅ cos ϕ
2 2
P
ωAD
ac = aB + aCB + aCB
τ
n
(b)
作加速度矢量图，P2 为BC的瞬心，而 P2C = 9 r
∴ ω BC =
vc 3 1 ωo = rω o ⋅ = P2 C 2 9r 6
2
aCB = BC ⋅ ω BC = 3 3r ⋅ (
n
ωo
6
)2 =
3 2 rω o 12
n
将 (b) 式在BC方向线上投影： ac = a B cos 30o − aCB =
r 2 3 3 3 2 2 ωo ⋅ − rω o = rω o 3 2 12 12
8-23 解： （1） v A = OA ⋅ ω AB 杆的速度瞬心为 O， 所以 AB 的角速度为ω， 因此： v B = OB ⋅ ω = 200 × 2 = 400 mm/s ω vA
由于 aa = ae + ae + ar + ar + aC
n n
va
M
v r = rw2 = 100 × 6 = 600(mm/s)
ω2
r O
vr
ω1
α1
arτ arn
A O
τ
τ
a
n e
aC
M
ae = 3rα1 = 3 × 100 × 3 = 900mm/s ar = rα 2 = 100 × 4 = 400mm/s
y
vD D
Q v A cos ϕ = v B = OB ⋅ ω ∴ ω AD OB ⋅ w v OB ⋅ ω cos ϕ = A = = PA PA PA ⋅ cos ϕ
2 2
P
ωAD
速度投影定理
速度投影定理[1]：同一刚体上任意两点的速度在这两点连线上的投影相等。
速度投影定理反映了刚体不变形的特性，这个定理对于任何形式的刚体运动以及刚体上的任意两点都成立，对此应能有所领会和认识。
速度投影定理：不可伸长的杆或绳绕一点转动时，尽管各点速度不同，但各点速度沿绳方向的投影相同。
简单证明：假设一条绳子上有两点A&B，两点的速度分别为VаVв。
因为A B 是刚体上的两点，他们之间的距离应保持不变。
所以两点的速度在绳子上的投影即直线上的分速度应该相同。
否则，线段不是伸长就是缩短。
因此，此定理不仅适用于刚体做平面运动，也适用于刚体做其他任意运动。
从速度投影到柯西不等式
例如 ， 求ｓ ｉ ｎ ｅ （ ３ —４ ｓ ｉ ｎ ０ ） 的极值．
（ １ － ｃ ｏ ｓ 口 ） ≤ ８ ｇ Ｌ （ 、 等 ） ， 一 劳Ｌ ‘ ， 当 丢 ｃ 。 ｓ 一 ｌ － Ｃ Ｏ Ｓ 目 ， 即 ｃ 。 ｓ ０ ＝ ２ Ｕ ￣ ， Ｂ 球 动 能 有 最 ≤ ÷ （ ± 专 ± ） ＝ ７ － （ ＿ 吾 ＿ ） ＝ ÷ ， 且 仅 当 ２ ｓ ｉ ｎ 一 ｓ 一 仅
＼Ｂ ｇ．
（ ３ ）如 图 ４设 杆 在 下 落 的 某
一
时刻与竖直 方 向的夹角 为 ０ ， 此
时 Ａ、 Ｂ 两 小 球 速 度 分 别 为
、
口 ｎ ， 则 有 Ａ ｃ ｏ ｓ ０ 一 ８ ｓ ｉ ｎ ０ ． 对 系 统 由功 能 关 系 可 得 ｍ ｎ ｇ Ｌ（ １ 一ｃ ｏ ｓ ０ ）
解析 ： ｓ ｉ ｎ （ ３ ４ ｓ ｉ ｎ ０ ） 一 ７ － ２ ｓ ｉ ｎ ０・２ ｓ ｉ ｎ ０・（ ３ ４ ｓ ｉ ｎ ０ ）
４ ｓ ｉ ｎ ， 即ｓ ｉ ｎ ０ ￣÷ 时成立． 所 以上式有最小值５ － ．
速 度 的 投 影 定 理 展 示 了 物理 模 型 的严 谨 与 简 约 ， 而 柯 西 不 等 式 则 折 射 出数 学 规 律 的精 密 与 细 腻 ， 都 向 我 们 传 递 着 科 学 的 内在 美 ． 而熟 练地 应 用 它们 则 会 增 加 我 们 的成 就 感 与进 一 步 学 习的 激 情 ． ３ 例 题 如 图 ３所 示 ， Ａ、 Ｂ 两 小 球 用 轻杆 连接 ， Ａ 球 只 能沿 内壁 光 滑 的
为零 势 能 面 ） ？ 解析 ： （ １ ）由速 度 的 投 影 定 理 知 Ａ 球 着 地 时 ， 一０ ，
１
刚体的平面运动
l 40
瞬时针方向
例2： 图示椭圆规。已知 ：AB =l=20㎝， vA=20㎝/s，φ=30°， C为杆AB的中点。试求 ：vB 、ωAB 、 vC 。
解： （1）分析各刚体的 运动，选取研究对象
选取AB作为研究对 象
（2）分析与AB连接点的运 动，选取运动已知的点 为基点
选A点 —— 基点（A点 运动已知）
解
(1)分析运动，确定基点。轮I做平面 运动，O点加速度可求，选其作为 基点。
(2)基点O的速度、加速度、轮I角速度
vo L 1，ao L12
vo r
L r
1
(3)求B点的加速度
aB ao aτBo aBno
v0
aτBo 0
aBno
r 2
L2 r
12
aB
ao2
aBnO
2
L1
1
vB= vA+ vBA
大小： ？ ？ 方向： （4）由三角关系求出所求量。
vA A r 900
o
l
vA
B
vB vBA
vB
vBA
vc
vCA
vA
B vA
AB
C vA
A
y
vB
vr =vBA
y'
r'B B
ve =vA
vA S
A
x'
0
x
1、定义
第三节 速度投影定理
平面图形上任意两点的速度在该两点连线上的投影相 等。——速度投影定理
vC vA2 vC2A 2vA vCA cos vA2 (AB l / 2)2 2vA (AB l / 2) cos
20(cm / s)
瞬时针方向
例2： 图示椭圆规。已知 ：AB =l=20㎝， vA=20㎝/s，φ=30°， C为杆AB的中点。试求 ：vB 、ωAB 、 vC 。
解： （1）分析各刚体的 运动，选取研究对象
选取AB作为研究对 象
（2）分析与AB连接点的运 动，选取运动已知的点 为基点
选A点 —— 基点（A点 运动已知）
解
(1)分析运动，确定基点。轮I做平面 运动，O点加速度可求，选其作为 基点。
(2)基点O的速度、加速度、轮I角速度
vo L 1，ao L12
vo r
L r
1
(3)求B点的加速度
aB ao aτBo aBno
v0
aτBo 0
aBno
r 2
L2 r
12
aB
ao2
aBnO
2
L1
1
vB= vA+ vBA
大小： ？ ？ 方向： （4）由三角关系求出所求量。
vA A r 900
o
l
vA
B
vB vBA
vB
vBA
vc
vCA
vA
B vA
AB
C vA
A
y
vB
vr =vBA
y'
r'B B
ve =vA
vA S
A
x'
0
x
1、定义
第三节 速度投影定理
平面图形上任意两点的速度在该两点连线上的投影相 等。——速度投影定理
vC vA2 vC2A 2vA vCA cos vA2 (AB l / 2)2 2vA (AB l / 2) cos
20(cm / s)
速度投影
vA
如果取速度瞬心C为基点，图形上任一点的速度就等于该点随图形绕点C 转动的速度。如图所示，点A、B、D的速度大小为
vA AC
vB BC
vD DC
A
vB
B
C
A D
vA
vA vD vB
B
C
平面图形的运动可以看成绕速度瞬心的瞬时转动。利用速度瞬心求解平面 图形上点的速度的方法，称为速度瞬心法。
AB
2 aBA aA vAsin l lcos l 2cos3
【例8-6】如图所示的半径为R的轮子在水平面上做纯滚动，已知轮心O的速度
与加速度分别为vO和aO，求轮子转动的角速度和角加速度，并求轮与水平面接
触点C的加速度。
O
aO vO
O
aC
aO
n aCO
，
C
aCO
故由点D的速度合成图，可知 vDA vA 0 (r1 r2 ) ,故轮II的角速度为
II
由B、C两点的速度合成图，有
2 2 vB v A vBA
20 (r1 r2 )
vC vA vCA 0 (r1 r2 )
0 (r1 r2 )
r2
A
解：轮II做平面运动，其上点A的速度为
vA
v A 0 OA 0 (r1 r2 )
以A为基点，分别分析三点B、C、D的
vB v BA
B
vA vA
D
vCA
A II
C
0
O
速度，分别画出速度合成图，由于vD=0，而
v DA
I
vD v A vDA
第八章 第二节 平面图形上各点的速度
100
小结速度分析的瞬心法解题步骤 总结平面运动速度分析三种方法(P182): (1)基点法: 基本方法。 可以求解图形上一点的速度或图形的角速度 (2)速度投影定理: 比较简单， 但只能求速度，不能求平面运动刚体的角速度 (3)瞬心法: 既简单直观(比基点法)， 又全面(比速度投影定理)
二、速度瞬心法(取速度瞬心为基点的速度分析方法) ［速度］瞬心(瞬时速度中心): 某一瞬时，刚体上速度等于零的一点vI =0 1．定理:一般情况下，在每一瞬时，平面图形上都唯一地存在 一个速度瞬心。 ［证明］ 见P177 2．平面图形内各点的速度及其分布
基点:速度瞬心 I vM = vI + vMI = vMI 任一瞬时，平面图形上任一点的速度 等于该点随图形绕瞬心转动的速度。 vM =MIw 方向垂直于MI
vA R r w wO r r v B BIw 2rw 2 ( R r )wO
vC CIw 2rw 2( R r )wO
v D DIw 2rw 2 ( R r )wO
wO
O I
I
A
w
B
例(P180例8-6) 曲柄滑块机构，曲柄OA的w=常量，杆长OA=r， AB=l，试求j=0、j=90°以及任一瞬时t时，连杆AB的角速度 和滑块B的速度。 wAB I j wt v A rw IA l cosy / cos j IB l cosy r cos j tanj vA A
速度合成定理:平面图形上任一点的速度等于基点的速度与该点 随图形绕基点转动速度的矢量和。
2. 速度投影定理(速度合成定理的推论) 定理:同一瞬时，平面图形上任意两点的速度在这两点连线上 的投影相等。 vB [证明] vB = vA + vBA vBA vA 投影到AB连线上 (vB )AB = (vA )AB + (vBA)AB (vB )AB = (vA )AB
08-理论力学-第二部分运动学第八章刚体的平面运动
形S在该瞬时的位置也就确定了。
88
运动学/刚体的平面运动
四、平面运动的分解 ——平移和转动
当图形Ｓ上Ａ点不动时，则
刚体作定轴转动 。
当图形Ｓ上 角不变时，
则刚体作平移。
故刚体平面运动可以看成是 平移和转动的合成运动。
例如：车轮的平面运动可以看成: 车轮随同车厢的平移 和相对车厢的转动的合成。
99
2121
如图示平面图形，某瞬时速度瞬心为P点， 该瞬时平面图形内任一点B速度大小
vB vP vBP vBP
B
大小：vB BP
方向：BP，指向与 转向相一致。
vB
S
vA
C
vC
同理:vA=ω·AP, vC=ω·CP
由此可见，只要已知图形在某一瞬时的速度瞬心 位置和角速度 ，就可求出该瞬时图形上各点的速度。
的平面Ⅱ内的运动。
66
运动学/刚体的平面运动
二、平面运动的简化 刚体的平面运动可以简化为
平面图形S在其自身平面内的运动。 即在研究平面运动时，不需考虑 刚体的形状和尺寸，只需研究平 面图形的运动，确定平面图形上 各点的速度和加速度。
三、平面运动方程 为了确定代表平面运动刚体的
平面图形的位置，我们只需确定平 面图形内任意一条线段的位置。
vBA
s
B
vB vA
A
vA
方向： AB, 指向与 转向一致。
即：平面图形上任一点的速度等于基点的速度与该点随
平面图形绕基点转动的速度的矢量和。 ——基点法
基点法是求解平面图形内一点速度的基本方法。 1414
运动学/刚体的平面运动
二、速度投影法
由于A, B点是任意的，因此
理论力学总复习
e
2
再选动点:滑块B; 动系: O1D; 静系: 机架。
根据
vBa vBe vBr
做出速度矢量图。
vBe 2ve 0.06 5
m/s,
vB vBa vBe / cos 0.15 vBr vBetg 0.03 5
做出加速度矢量图
m/s
m/s
n 根据 aBa aBe aBe aBr aBk
2．定轴转动刚体
3．平面运动刚体
1 T J z 2 2
1 T J P 2 （P为速度瞬心） 2
1 1 2 M vC J C 2 2 2
四．质点系的动能定理
T2 T1 W
•求速度定用动能定理； •若机构中有平面运动的物体，求机构的运动量，用动能定
理；
•求定轴转动刚体的角加速度，用定轴转动刚体的转动微分 方程最简单；
感谢大家的支持与配合
祝期末考试取得优异成绩！
求：该瞬时顶杆 AB的速度和加速度。 解: 动点: 顶杆上A点； 动系: 凸轮 ; 静系: 地面。 绝对运动: 直线;
绝对速度: va=? 待求, 方向沿AB;
相对运动: 曲线; 相对速度: vr=? 方向n; 牵连运动: 定轴转动; 牵连速度: ve= r ， 方向OA，
根据速度合成定理 va
理论力学总复习
运动学
运动学部分重点内容： 1.运动学基础
2.点的合成运动
速度合成定理
va = vr + ve
常用几何法,作速度合成图,最后归结为解三角形。 加速度合成定理 牵连运动为平动 aa = ar + ae aa = ar + ae + ak
牵连运动为定轴转动
2
再选动点:滑块B; 动系: O1D; 静系: 机架。
根据
vBa vBe vBr
做出速度矢量图。
vBe 2ve 0.06 5
m/s,
vB vBa vBe / cos 0.15 vBr vBetg 0.03 5
做出加速度矢量图
m/s
m/s
n 根据 aBa aBe aBe aBr aBk
2．定轴转动刚体
3．平面运动刚体
1 T J z 2 2
1 T J P 2 （P为速度瞬心） 2
1 1 2 M vC J C 2 2 2
四．质点系的动能定理
T2 T1 W
•求速度定用动能定理； •若机构中有平面运动的物体，求机构的运动量，用动能定
理；
•求定轴转动刚体的角加速度，用定轴转动刚体的转动微分 方程最简单；
感谢大家的支持与配合
祝期末考试取得优异成绩！
求：该瞬时顶杆 AB的速度和加速度。 解: 动点: 顶杆上A点； 动系: 凸轮 ; 静系: 地面。 绝对运动: 直线;
绝对速度: va=? 待求, 方向沿AB;
相对运动: 曲线; 相对速度: vr=? 方向n; 牵连运动: 定轴转动; 牵连速度: ve= r ， 方向OA，
根据速度合成定理 va
理论力学总复习
运动学
运动学部分重点内容： 1.运动学基础
2.点的合成运动
速度合成定理
va = vr + ve
常用几何法,作速度合成图,最后归结为解三角形。 加速度合成定理 牵连运动为平动 aa = ar + ae aa = ar + ae + ak
牵连运动为定轴转动
理论力学第九章刚体的平面运动
O 基点
转角
基点的选取是任意的，平面图形的位置可由O’点 坐标及直线O’M与x’的夹角φ 完全确定。 基点的选择不同，其运动方程9-1a不同，平面图形随基 点平移的速度和加速度也不同。但平面图形绕不同基 点转动的角速度和角加速度却完全相同。证明如下
f (t ) f (t ) 3 3
结 论
刚体的平面运动可以简化为平面图形S 在其自身平面L上的运动。
6
2、运动分析
思考
刚体平面运动是复杂运动，考虑是否可以用 简单运动合成来分析？
Oxy 平移坐标系(动系) 平面运动=随 Oxy 的平移+绕 O 点的转动
=
+
7
3 运动方程
xO f1 t 9-1a yO f 2 t f3 t 9-1b
vB AB = vA
OA
vD
vB
vB
cos30 2 CD作定轴转动（C）
0.2309 m s
vE
vA
vB vD CD 3vB 0.6928 m s CB
vD vE DE = vD ,vE cos 30 vD , vE cos 30 0.8 m s
第九章 刚体的平面运动
本章重点：刚体平面运动的基本概念，求平面图形上各 点的速度与加速度的基点法，以及求速度的 速度投影法和瞬心法，运动学的综合应用。
1
刚体平面运动举例：行星齿轮中小齿轮运动情况
2
车轮运动情况
3
观察曲柄滑块机构中连杆AB的运动情况
4
§ 9-1
1、概念
刚体平面运动的概述和运动分解
30
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y
O1
O O
A
B
x
刚体平面运动的实例演示
8.1.2 刚体平面运动的简化
根据平面运动的定义可知，在刚体运动过程中，此平面图形必在平面II内
运动。在刚体内任取一条垂直于平面图形S的直线A1A2做平动。点A的运动代表
了A1A2上所有各点的运动。过平面图形S作无数条垂线，这无数条垂线与平面 图形有无数个交点，这无数个交点的运动代表了无数条直线的运动。刚体的平
BA
A
vA
解：杆AB做平面运动，先进行速度分析，以A为基点分析点B的速度。
vB vA tan
故杆AB的角速度为
vBA vA / cos
AB
vBA
BA
vA l cos
然后再进行加速度分析和计算，以A为基点分析点B的加速度。
n 列 aBA 方向的投影方程
n aB cos aAcos(90 ) aBA
故由点D的速度合成图，可知 vDA vA 0 (r1 r2 ) ,故轮II的角速度为
II
由B、C两点的速度合成图，有
2 2 vB v A vBA
20 (r1 r2 )
vC vA vCA 0 (r1 r2 )
0 (r1 r2 )
r2
vBx 3 0 r，vBy 3 0 r， AB 3 0， BC 2 0
y
C A D
B
30
0
a BC
aBA
30
n a BC
O
0
30
n a BA
B
n aA
n aC
x
，
再由加速度合成图可知：
n n n aBx aBA aC aBC sin30 aBC cos30 n n aBy aBA a A aBC cos30 aBC sin30
AB
2 aBA aA vAsin l lcos l 2cos3
【例8-6】如图所示的半径为R的轮子在水平面上做纯滚动，已知轮心O的速度
与加速度分别为vO和aO，求轮子转动的角速度和角加速度，并求轮与水平面接
触点C的加速度。
O
aO vO
O
aC
aO
n aCO
，
C
aCO
B
aA
n a BA
a BA
解得
aB
aB a A tan
vA l cos
3
aBsin aAcos aBA
2
BA
A
aA
列 aBA 方向的投影方程
解之得
a
BA
2 aA vAsin aBsin aAcos cos lcos3
所以，AB杆的角加速度为
C
aO
解：轮子在水平面上做纯滚动，轮子和水平面的接触点C为其速度瞬心。
根据轮心O的速度和加速度，轮子的角速度和角加速度可分别表示为
vO R
d d vO 1 dvO a O ( ) dt dt R R dt R
O
aO vO
O
aC
aO
n aCO
C
aCOBiblioteka CaOn 以轮心O为基点，分析点C的加速度，由加速度合成定理 aC aO aCO aCO ，
即
AB
P
cos PA l cos
代入可得
sin( ) PB l cos
O
vA
A
AB
r PA
r cos l cos
r sin( ) cos
vB
B
vB PB AB
例8-4 如图所示的圆轮转动的角速度为 求圆轮中心O和轮缘上两点A、B的速度。
8.3.2 平面图形上速度瞬心的求法
如图给出了各种条件下速度瞬心的求法。
A
B
vA
A
vA vB
P
P
vB
B
A
vA vB
B
P
P
若轮子沿着固定的轨 道只滚不滑，那么轮 子和轨道接触点在瞬, 时处于静止，因此该 点就是此瞬时的速度 瞬心。
在某瞬时，如果平面图形内各点的速度相等，称此时刚体做瞬时平移。必 须注意，做瞬时平动的刚体，在其平面图形上没有速度瞬心，此瞬时刚体内各 点的速度相等，但加速度不相等。
2rad / s
，试用速度瞬心法
解：圆轮做平面运动，轮与地面的接触点 P为轮的速度瞬心。因此，三点O、A、B的速 度可分别表示为
A
vA
vO PO 2 0.75 4.71m / s
vB
B
O
vO
vB PB 2 2 0.75 6.66m / s
r2 20 (r1 r2 )
8.2.2 速度投影定理
速度投影定理：刚体上任意两点M和O'的速度在此两点连线上的投影彼此 相等，即
[vM ]OM [vO ]OM
证明:如图所示，以O'为基点分析动点M 的速度，由速度合成定理，可得
v MO'
vM
vM vO' vMO'
将上式投影到直线O'M上，有
8.1.4 平面运动的分解
设有平面图形S在其自身平面内做平面运动，连线AB的位置可代表平面图 形的位置。设平面图形S在△t 时间内从位置I 运动到位置II，其内的直线由位 置AB移到A' B'。可将直线AB位置的变化分成两步来完成。如图所示 。从上 面的分析可知,平面运动可以分解为随基点的平动和绕基点的转动。
A
vA
B
vB
A B
vA vB
【例8-3】 曲柄滑块机构图所示，已知AB=l，OA=r，杆OA转动的角速度为ω , 杆OA与水平线间的夹角为 ，杆AB与水平线间的夹角为 。求杆AB转动的角 速度ωAB和滑块B的速度vB。
AB
P
解：连杆AB做平面运动，P为杆AB的 速度瞬心。由于A点的速度可表示为
面运动,可简化为平面图形在其自身平面内的运动。
A1
S
II A
I
A2
8.1.2
刚体平面运动的简化
8.1.3 刚体平面运动方程
如图所示为一平面图形在其自身平面Oxy平面上的运动。要确定平面图形
(刚体)的位置,只需确定其中任一直线的位置。而要确定此直线在平面Oxy的位
置，只须确定点O′的位置和夹角即可，即
y
M
xO' f1 ( t ) yO' f 2 ( t ) f (t ) 3
上式称为刚体平面运动方程。
O
O'
x
如果图形中点O'固定不动，则平面图形绕基点O' 做定轴转动；如果线段O'M 的方位不变，则平面图形作平动。由此可见，刚体的平面运动可以看成随基点平
动和绕基点的转动的合成。
刚体平面运动的概述和运动 分解
8.1 8.2 8.3 平面运动概述 用基点法求平面图形内各点速度 用瞬心法求平面图形内各点速度
8.4
8.5
用基点法求平面图形内各点的加速度
运动学综合应用举例
8.1 平面运动概述 8.1.1 刚体平面运动的特征
左图所示的行星轮绕固定轮的滚动，右图所示的曲柄连杆机构中连 杆的运动等，这些刚体的运动既不是平动，也不是定轴转动，但它们 的运动有一个共同特征，即刚体在运动过程中，其上任一点与某一固 定平面的距离始终保持不变。这种运动称为刚体的平面运动。
P
vA PA 2 1.5 9.42m / s
其方向分别垂直于三点O、A、B和点P连线，并且与轮子转动的方向一 致。方向如图所示。
8.4 用基点法求平面图形内各点的加速度
如图所示，用一平面图形表示一刚体做平面运动。设某瞬时，平面图形内
某一点O的加速度为aO，平面图形的角速度为ω ，角加速度为ε ，求平面图形 内任一点M的加速度aM。
y
平面运动中平动部分与基 点位置的选择有关，而转动部 分却与基点位置的选择无关。
S
y' B
B'
B''
A''
A'
A x'
平面图形转动无须标明绕哪一 点转动。
O
II
I
x
8.2 用基点法求平面图形内各点速度
8.2.1 用基点法求平面图形内一点的速度
可用点的速度合成定理求点M的速度，即
v MO'
vM
O
vA
A
v A OA PA AB
可得做平面运动的杆AB角速度
vB
B
AB
滑块B的速度可表示为
OA r PA PA
vB PB AB
而由正弦定理，可知
AB PA PB sin(90 ) sin(90 ) sin( )
如图所示。
B
由速度合成图可知
vA
vB v A tan
v BA vB
vBA v A / cos
故杆AB的角速度为
BA
A
vA
BA
vBA
BA
vA
l cos
【例8-2】 如图所示的行星轮系中，已知大齿轮I固定，半径为r1；行星齿轮II 沿轮I只滚动而不滑动，半径为r2，系杆OA角速度为ω0。试求轮II的角速度ωII vC 及其上B、C两点的速度 v