圆柱螺旋弹簧设计计算表
圆柱螺旋压缩弹簧计算

D+d 265 D-d 175 arc tan t/πD 0.10002485 0.1003598 0.001447 691.15 πDn1 / cosα 16671 1.005 0.995002 1447.54 1101.38 1059.00 346.1681845 0.3 0.9 7.245454545 2.6 1 / Pj 1/D 1.09E-05 0.004545 P1/ P' Pn / P' Pj / P' 146.4558 492.624 535.0029
圆柱弹簧设计计算
最小输出扭矩M(Nm) 最大输出扭矩M(Nm) 驱动半径R(m) 驱动半径R(mm) 弹簧最小输出力 P1(N) 弹簧最大输出力 Pn(N) 工作行程 L(m) 工作行程 h(mm) 最大最小输出力差 Δ P(N) 初算弹簧刚度 P'(N/mm) 工作的极限载荷 Pj(N) 初选材料直径d及中径D 弹簧 有效圈数 n 总圈数 n1 弹簧刚度 P'(N/mm) 工作极限载荷下的变形量 Fj 节距 t(mm) 自由高度 H0(mm) 取标准值 H0(mm) 弹簧外径 D2(mm) 弹簧内径 D1(mm) 螺旋角 α (弧度) 展开长度 L(mm) Mmin Mmax R R P1 Pn L h Pn-P1 ΔP / h K × Pn d 45 P'd / P' n+2 P'd / n n × fj Fj / n+d nt + 1.5d 5500 18500 0.22 倒数 1/R 4.545455 220 25000 84090.90909 0.3454 345 倒数 1/h 0.002895 59090.90909 171.0796442 倒数 1/P' 0.005845 92500 D 220 21.94884154 24 170.6818182 535.04 69.36363636 1593.5 1594 系数 K Pj 91325 取整 取整 取整 Fj / n nt 1.1 fj 24.32 22 170.7 536 24.36364 1526 P'd 3755 倒数 倒数 倒数 1.5d 0.045455 0.005858 0.001866 67.5
圆柱压缩弹簧计算表

弹簧中径D mm安装高度H1mm压缩长度f mm初始载荷F 1 N68105400弹簧载荷类别弹簧材料假设丝径d mm抗拉强度σb Mpa Ⅰ类50CrVA71520查表7.1-6Ⅰ类Ⅱ类Ⅲ类弹簧刚度kN/mm安装变形量校核f1 mm 安装变形量取值f1 mm 安装高度取值H1 mm5.80041642968.9605660170230受循环载荷次数大于100万次受循环载荷次数小于1000次1. 选择材料与许用切应力受循环载荷次数大于1000次小于100万次基本数据4.弹簧刚度、载荷和变形量的校核根据机械手册所做的压缩弹簧计算表,所有参k =G ⅆ48nD 3f 1=F 1k工作载荷F 2 N1000许用切应力τp Mpa切变模量G Mpa 旋绕比 C 曲度系数K532790009.714285714 1.125查表7.1-8 0.35σb查表7.1-4D/d 查图7.1-4工作变形量f2 mm 安装载荷F1 N 工作载荷F2 N 自由高度H0 mm压并高度Hbmm175406.029151015.0728********.5f2=f1+f F1=f1*k F2=f2*k H0=H1+F1Hb=n1*d节距 mm δ1 mm 22.969230770.7一般取值>=0.1*d校核校核弹簧特性所有参数请查阅机械设计手册2. 弹簧钢丝直5. 自由高度、压并高度弹簧的其余尺1p =d +f b n+δ1计算直径d mm 直径取值 dmm 弹簧刚度k 弹簧有效圈数有效圈数取值n 总圈数 n 17.2518007697.0 5.71428571413.195947371314.5支撑圈数取值n 21.5压并变形量f b mm198.5fb=H0-Hb 螺旋角α °6.1368438660.107519606α=arctan(p/πD)钢丝直径mm 3. 弹簧有效圈数并高度和压并变形量 6.实验载荷和试验载荷下的变形量其余尺寸参数1.6KCF 2τpF f =F1−F2f1−f2n =G d 48D 3k。
圆柱螺旋压缩(拉伸)弹簧的设计计算

圆柱螺旋压缩(拉伸)弹簧的设计计算
一、圆柱螺旋压缩(拉伸)弹簧的设计原理
1、圆柱螺旋压缩(拉伸)弹簧原理
圆柱螺旋压缩(拉伸)弹簧是一种特殊的弹簧,其结构设计使用了螺
旋结构,螺旋结构的形状是一个圆柱形的圆柱螺纹。
圆柱螺旋压缩(拉伸)弹簧的压缩(拉伸)受力分布差异,当进行压缩(拉伸)力作用时,弹簧
的整个螺旋节在不同的力矩作用下会产生相应的弹性变形,从而使得弹簧
的中心轴变长,以缩短弹簧的长度。
2、圆柱螺旋压缩(拉伸)弹簧特性
圆柱螺旋压缩(拉伸)弹簧具有对同直径和外径的小变化具有很强的
适应性的特性,同时,压缩(拉伸)力也有必要时可以根据弹性变形率来
改变。
圆柱螺旋压缩(拉伸)弹簧的压缩(拉伸)受力分布差异,当进行
压缩(拉伸)力作用时,弹簧的整个螺旋节在不同的力矩作用下会产生相
应的弹性变形,从而使得弹簧的中心轴变长,从而缩短弹簧的长度。
此外,这种弹簧具有紧凑结构,能够有效地减少设备装置内的多余空间,重量轻,由于采用细小的钢、不锈钢、铜或其它有良好装配性的金属等材料,具有
良好的耐磨性、耐腐蚀性和耐臭氧性等性能。
圆柱螺旋弹簧一般计算公式

1. 弹簧刚度:
2. 力值: 其中:G 为材料剪切模量,一般不锈钢取71500Mpa,碳钢取
78500Mpa ;
d 为材料直径;
D 为弹簧中径;
n 为弹簧有效圈数;
f 为变形量(拉压行程)。
3. 应力: K 为曲度系数,公式为: 其中C 为弹簧旋绕比,是弹簧中径与线径的比值,即
4. 下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力,加上初拉力就行。
初拉力: 其中初拉力τ0按初切应力图选取,见下图。
三.扭簧:
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径;
E---材料的弹性模量,一般不锈钢丝取188000Mpa ,碳素钢丝
取206000Mpa ;
D---弹簧外径;
ϕ---弹簧的扭转行程(角度);
4. 应力: K1为曲度系数,顺旋向扭转取1,逆旋向扭转时按下式:
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。
DIN 圆柱螺旋压缩弹簧计算和设计
5.1 静负荷和准静负荷 静负荷为: 不随时间变化的负荷 准静负荷为: 随时间变化但位移应力很小,以致可忽略的负荷(标准值:位移应力达 0.1 × 连续行程疲劳强度) 随时间变化,而且位移应力较大,但负载循环数达到 104 的负荷
5.2 动负荷 弹簧的动负荷为: 随时间变化,负载循环数超过 104,位移应力超过 0.1 × 连续行程疲劳强度的负荷,且在以下情
第 2 页 DIN 2089 第一部分
2 理论压缩弹簧图
弹力
弹簧行程
弹簧长度
图 1. 理论压缩弹簧图 根据 DIN 2095 和 DIN 2096 第 1、2 部分描绘和制作压缩弹簧并给出试验图。
DIN 2089 第一部分 第 3 页
3 常用符号、单位和名称
常用符号 单位
名称
a0
mm 无负荷弹簧上有效弹簧圈之间的内侧距离
8 计算公式……………………………………5 9.1 在闭塞长度上的允许剪应力 …………12
8.1 弹性功………………………………………5 9.2 在静或准静负荷时的允许剪应力………12
8.2 弹性力………………………………………5 9.3 动负荷时的允许位移应力………………18
1 应用范围
该标准适用于直径不变的圆形簧丝和棒构成,且具有线性特性曲线的圆柱形螺旋压力弹簧的计 算和设计,而且这些弹簧的主要负荷处于弹性轴上,其质量规范在 DIN2095 和 DIN2096 第 1 和第 2 部分中已有规定。因此适用以下极限值:
Kn
τKh τKH(…) τKU(…) τKO(…)
τzul τSt
N/mm2 N/mm2 N/mm2
N/mm2
N/mm2 N/mm2 N/mm2 N/mm2 N/mm2 N/mm2
弹簧设计计算

项目 最小工作载荷P1 最大工作载荷Pn 工作行程h 弹簧中径D 弹簧直径d 原 弹簧类别 始 条 端部结构 件 旋绕比C 曲度系数K 弹簧材料 材料极限切应力 材料切变模量 初算弹簧刚度P' 工作极限载荷Pj 单位 N N mm mm mm 公式及数据 2000 7570 170 80 14 III类 端部并紧、磨平,两端支承圈各1圈 C= 5.714285714 K= 1.266715909 60Si2Mn MPa τj= 740 MPa G= 79000 N/mm P'= 32.76470588 N Pj= 7868.763643 P1= Pn= h= D= d= fj= 10.62006597 P'd= 740.9335938 n= 22.613772 取 n= n1= 30 P‘= 26.46191406 Fj= t= H0= D2= D1= α= L= H1= Hn= Hj= h= 下限 上限 b= 297 24.61 710.08 取H0= 94 66 5.592578199 7576 634.42 423.93 412.64 210.49 0.25 0.96 81、根据弹簧套筒内径以及旋绕比C 5~8初步确定 弹簧直径与中径; d 3 j 2、由极限载荷公式 Pj 8DK 可知,极限载荷 只由中径、直径以及材料有关,与施加的外力无关 。故一旦中径、直径以及材料确定后,弹簧的极限 载荷就是一定值; 3、根据 弹簧的工作范围为20%~80%初步确定最小工作载荷 以及最大工作载荷;最小工作载荷应大于推动侧护 板所需要的力; 4、根据以上 最终验算结果,对以上各值进行调整
工作极限载荷下的 mm 单圈变形量fj 单圈弹性刚度P'd N/mm 有效圈数n 圈 总圈数n1 圈 N/mm 参 数 弹簧刚度P’ 计 算 工作极限载荷下的 变形量Fj mm 节距t mm 自由度高H0 mm 弹簧外径D2 mm 弹簧内径D1 mm 螺旋角α (°) 展开长度L mm 最小载荷时高度H1 mm 最大载荷时高度Hn mm 极限载荷时高度Hj mm mm 验 算 实际工作行程h 工作范围 高径比b
弹簧设计计算软件
L=n*l+钩 mm 316.44 环展开尺
寸
计算
公式
661.5 N/mm2
78500 N/mm2 203000 N/mm2
备注
2.16 mm
Mn'>Mn
合理
8
n)/(3667* Mn*D)= φn/Ψn=
23 工作极限扭矩 Mj
N.mm
787.5
Mj=(d^3* [σ BP])/(10* K)
24 最小工作扭矩 M1 25 工作极限扭矩下扭转角 φj
N.mm (°)
295
M1=φ 1/(Ψ'*n)
88 φj=Ψ '*n*Mj
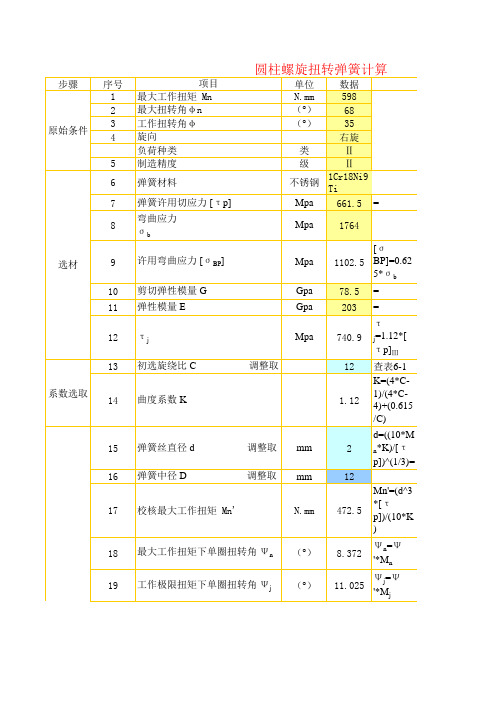
步骤 原始条件
选材
系数选取
序号 1 2 3 4 5 6 7 8
9 10 11 12 13
14
15 16
17
18
19
项目 最大工作扭矩 Mn 最大扭转角φn 工作扭转角φ 旋向 负荷种类 制造精度
弹簧材料
弹簧许用切应力 [τp] 弯曲应力 σb
许用弯曲应力 [σBP]
剪切弹性模量 G 弹性模量 E
圆柱螺旋扭转弹簧计算
(°) (°)
8.372 11.025
Ψn=Ψ '*Mn
Ψj=Ψ '*Mj
公式
Ψ
'=(3667*
20 在1N.mm扭矩作用下单圈扭转角Ψ' (°) 0.014 D)/(E*d^ 4)=Ψ
n/Mn l=((π
21 弹簧单圈展开长度 l
mm
37.68
*D)^2*t^ 2)^(1/2)
≈π*D
参数计算 22 有效圈数 n
26 最小工作扭矩下扭转角 φ1
弹簧计算

′
13.73239437
mm
= +d
5.068
自由高度H0
mm
H0=nt+1.5d
75.452
弹簧外径D2
mm
D2=D+d
19
弹簧内径D1
mm
D1=D-d
13
mm
最小载荷时的高
度H1
mm
最大载荷时的高
度Hn
mm
极限载荷时的高
度Hj
mm
实际工作行程h
mm
工作区范围
高径比 b
Fj=nfj
α =
π
πD1
=
1
1 = 0 −
′
′
= 0 −
′
= 0 −
h=H1-Hn
1
; ;
0
=
根据机械设计手册表查得标准
值
14
取标准值
75
12.1875
节距t
展开长度 L
根据机械设计手册表查得
16
mm
(°)
弹簧类别Ⅱ时 Pj≥1.25Pn
弹簧类别Ⅲ时 Pj≥Pn
195
′
= ′
工作载荷下的变
形量Fj
螺旋角α
算
N/mm
碳素弹簧钢丝C级
− 1
′ =
14.2
ℎ
N
单圈刚度 P'd
验
1000000
工作极限载荷Pj
所选弹簧 工作极限载荷Pj
数据
工作极限载荷下
的单圈变形量fj
28.952
5.763193109
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱螺旋弹簧设计计算表
4 - 16
外径Demax. 350 mm工作线圈数nmin. 3比
率b/h1:5 - 5:1自由长度L0max. 1500 mm长细
比L0/D1 - 15间距p(0.2 - 0.4) D - 无预压弹簧
弹簧收尾设计
.
A =半圈
B = 整圈
C = 侧面整圈
D =双扭曲整圈
E = 侧面双扭曲整圈
F = 内部整圈
G =. 提高的挂勾H = 侧面提高的挂勾L = 锥形旋转小圈收尾I = 小圈J = 侧面小圈K = 倾斜的整圈
M = 锥形旋转螺栓收尾N = 螺丝状收尾O = 螺丝状束缚收尾
拉伸弹簧通常使用几种不同高度和特性的挂钩来固定(A..J)。
从技术角度讲,固定挂钩是最好的解决方案,但是,这也带来弹簧负载的一些确定问题。
弹簧负载带给挂钩集中的负载应力,该负载应力可能明显地高于弹簧线圈所计算的应力。
针对在挂钩中产生的弯曲应力,小圈(类别 I, J)或双圈(类别 D, E)是最佳方案。
针对由线变成线圈所产生的集中的扭转应力,侧边整圈(类别 C,E,I)是最佳方案。
对于挂钩的独立设计,以下挂钩高度值指定如下:
热成型弹簧,方形线圈弹簧以及循环负载弹簧通常无弹簧卡钩使用(M..O. design)。
无固定挂钩弹簧使用边缘线圈固定,弹簧功能变形中线圈间距不会变化。
