1.7 极限存在准则 两个重要极限-习题
1-7存在准则两个重要极限

例1 求 lim( 1 1 1 ).
n n2 1 n2 2
n2 n
解 n 1 1 n ,
n2 n n2 1
n2 n n2 1
又 lim n
n lim n2 n n
1 1 1 1,
n
lim n lim 1 1, 由夹逼定理得
n n2 1
n
1
1 n2
lim( 1 1 1 ) 1.
x [x]
x [x]
x [x]
lim (1 1 )[ x] x [x] 1
lim (1 1 )[ x]1 lim (1 1 )1 e,
x [x] 1
x [x] 1
lim (1 1 )x e.
x
x
令 t x,
lim (1 1 )x lim (1 1)t lim (1 1 )t
7、 lim(1 x )2x _________. x x
8、 lim(1 1 ) x _________.
x
x
二、求下列各极限:
1、 lim 1 cos 2x x0 x sin x
2、 lim(tan x)tan 2x x 4
3、 lim( x a ) x x x a
4、 lim( n2 1)n n n 1
sin x x tan x, 即 cos x sin x 1, x
上式对于 x 0也成立. 当 0 x 时,
2
2
0 cos x 1 1 cos x 2sin 2 x 2( x)2 x2 , 22 2
lim x2 0, lim(1 cos x) 0,
x0 2
2、 lim sin 2x __________. x0 sin 3x
3、 lim arc cot x __________.
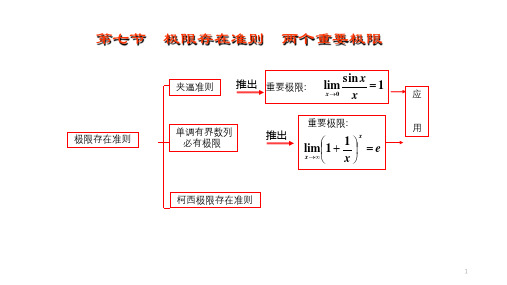
极限存在准则两个重要极限

sin x 即 cos x < < 1, x
π 上式对于 − < x < 0也成立. 2
当 0 < x < 时, 2
π
2 x x 2 x , = 2 sin 2 < 2( ) = 0 < cos x − 1 = 1 − cos x 2 2 2
x2 Q lim = 0, x →0 2
∴ lim cos x = 1,
x
+9
1 x x
)
= lim (9
x → +∞
x
1 x x
)
1 x + 1 3
0
1 x
3 1 = 9 ⋅ lim 1 + x x → +∞ 3
1 3x ⋅x
= 9⋅e = 9
∴ {xn } 是单调递增的 ;
1 1 1 1 xn < 1 + 1 + + L + < 1 + 1 + + L + n −1 2! n! 2 2 1 = 3 − n − 1 < 3, ∴ {xn } 是有界的 ; 2 1n ) ∴ lim x n 存在. 记为lim(1 + ) = e (e = 2.71828L n→∞ n→∞ n
x→0
∴ lim(1 − cos x ) = 0,
x→0
又 Q lim 1 = 1,
x→0
sin x sinx ∴lim = 1. x→0 x
注
此结论可推广到
sinϕ( x) lim =1 x→a ϕ( x)
条件是x → a时,ϕ( x) → 0,其中a可为 有限值, 有限值,也可为∞
(完整版)1-7两个重要极限练习题

1-7 两个重要极限练习题教学过程:引入:考察极限xx x sin lim 0→当x 取正值趋近于0时,x x sin →1,即+→0lim x xx sin =1;当x 取负值趋近于0时,-x →0, -x >0, sin(-x )>0.于是)()sin(lim sin lim 00x x x x x x --=+-→-→. 综上所述,得一.1sin lim0=→x xx .1sin lim 0=→xxx 的特点:(1)它是“00”型,即若形式地应用商求极限的法则,得到的结果是0;(2)在分式中同时出现三角函数和x 的幂.推广 如果ax →lim ϕ(x )=0,(a 可以是有限数x 0, ±∞或∞),则 ax →lim()[]()x x ϕϕsin =()()[]()x x x ϕϕϕsin lim 0→=1.例1 求xxx tan lim0→.解 x x x tan lim 0→=111cos 1lim sin lim cos 1sin lim cos sin lim 0000=⋅=⋅=⋅=→→→→xx x x x x x x x x x x x .例2 求x xx 3sin lim 0→.解 x x x 3sin lim 0→=3sin lim 3)3(33sin 3lim 00==→→ttt x x x t x 令.例3 求20cos 1lim xxx -→. 解 20cos 1limx xx -→=2122sin22sin 21lim )2(22sin lim 2sin 2lim0220220=⋅⋅==→→→x xx x x x x x x x x .例4 求xxx arcsin lim0→.解 令arcsin x =t ,则x =sin t 且x →0时t →0. 所以x x x arcsin lim0→=1sin lim 0=→ttt .例5 求30sin tan lim xxx x -→. 解 30sin tan lim x x x x -→=3030cos cos 1sin lim sin cos sin lim xx xx x x x x x x -⋅=-→→ =21cos 1lim cos 1lim sin lim2000=-⋅⋅→→→xx x x x x x x . 考察极限e xx x =+∞→)11(lim当x 取正值并无限增大时,x x )11(+是逐渐增大的,但是不论x 如何大,x x )11(+的值总不会超过3.实际上如果继续增大x .即当x →+∞时,可以验证x x)11(+是趋近于一个确定的无理数e =2.718281828....当x →-∞时,函数x x)11(+有类似的变化趋势,只是它是逐渐减小而趋向于e .综上所述,得二.x x x)11(lim +∞→=e .xx x)11(lim +∞→=e 的特点:(1)lim(1+无穷小)无穷大案;(2)“无穷小”与“无穷大”的解析式互为倒数.推广 (1)若ax →lim ϕ(x )= ∞,(a 可以是有限数x 0, ±∞或∞),则 ()[])()()(11lim ))(11(lim x x x ax x x ϕϕϕϕϕ+=+∞→→=e ;(2)若ax →lim ϕ(x )=0,(a 可以是有限数x 0, ±∞或∞),则[()]()[()])(10)(11lim1lim x x x ax x x ϕϕϕϕϕ+=+→→=e .变形 令x1=t ,则x →∞时t →0,代入后得到 ()e t t t =+→101lim .如果在形式上分别对底和幂求极限,得到的是不确定的结果1∞,因此通常称之为1∞不定型.例6 求x x x )21(lim -∞→.解 令-x 2=t ,则x =-t2.当x →∞时t →0,于是 x x x)21(lim -∞→=21020])1(lim [)1(lim -→-→+=+t t t t t t =e –2.例7 求xx x x )23(lim --∞→.解 令x x --23=1+u ,则x =2-u1.当x →∞时u →0, 于是 xx xx )23(lim --∞→=])1()1[(lim )1(lim 210120u u u u u u u +⋅+=+-→-→=])1(lim [])1(lim [2011u u u uu +⋅+→-→=e -1.例8 求x x x cot 0)tan 1(lim +→.解 设t =tan x ,则t1=cot x . 当x →0时t →0, 于是 xx x cot 0)tan 1(lim +→=tt t 10)1(lim +→=e .小结:两个重要极限在求极限过程中有着很重要的作用,特别要注意其变式。
极限存在准则 两个重要极限

∴ {xn } 是单调递增的 ;
1 1 1 1 xn < 1 + 1 + + L + < 1 + 1 + + L + n −1 2! n! 2 2 1 = 3 − n − 1 < 3, ∴ {xn } 是有界的 ; 2 1n ) ∴ lim x n 存在. 记为lim(1 + ) = e (e = 2.71828L n→∞ n→∞ n
x → +∞
)
= lim (9
x → +∞
x
1 x x
)
1 x + 1 3
0
1 x
3 1 = 9 ⋅ lim 1 + x x → +∞ 3
1 3x ⋅x
= 9⋅e = 9
∴ lim cos x = 1,
x→0
∴ lim(1 − cos x ) = 0,
x→0
又 Q lim 1 = 1,
x→0
sin x ∴lim = 1. x→0 x
例3
1 − cosx . 求 lim 2 x→0 x
x 2sin2 2 lim 2 x→0
解: 原式 =
x
1 sin = lim x 2 x→0 2
1 令t= , x
x→0
1t lim(1 + x) = lim(1 + ) = e. x→0 t →∞ t
1 x
1 x
lim(1 + x) = e
例.
解: 令 t = −x, 则
t →∞
lim(1+ 1)−t t
1
= lim
§1-7j极限存在准则与两个重要极限

, sin x 0 , sin x x tan x 2 sin x 1 1 cos x , x
得
1
x 1 , sin x cos x
1式 也 成 立 .
lim cos x 1
x 0
x 0
sin x 1. 由夹逼准则知 lim x
推广:
lim
sin
x 1 解 lim x x 1
x
x x x x lim ( ) ( ) 1 1 x x x 1 x 1 解 lim lim lim x 1 x e x x 1 x x x (1 ) lim x x x 1 x 1
n 2 2 2 2 2
解
存在 , 并求极限. 1 1 1 2 2 k 1,2, , n, 2 2 n k n2 12 n n 1 1 1 n 1 n 2 2 2 2 2 2 2 2 n 1 2n n n n 1 n 2 n n
12
t年末的本利和为
r mt Am (t ) A0 (1 ) m
若期数无限增大,即令 m , 则表示利息随时 计入本金,这样t年末本利和为
A(t ) lim Am (t ) lim A0 (1
m m
r mt ) m
r m rt = A0 lim (1 ) r A0 e rt m m
8
1 1 1 2. lim 1 e lim 1 e lim( 1 x ) x e n x x 0 n x
n
x
利用准则2,可以证明第二个重要极限
特点 1.幂指函数; 2.底数是1与无穷小量之和; 3.指数是无穷大量,且与底数中的无穷小量成倒数关系.
高等数学 第1章 第七节 极限存在准则 两个重要极限
则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,(舍去)
lim n
xn
3.
14
3.两个重要极限的应用
例6: 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解: lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知:
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明:
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x
极限存在准则.两个重要极限

例13 求 lim x 1 2x x0 1
解 原式 lim(1 2x) x (1 型) x0
lim(1
2
x
)
1 2x
2
(lim(1
2
x)
1 2x
)2
e2.
x0
x0
例14 求 lim(1 sin x)csc x (1 型)
x0
1
解 原式 lim(1 sin x)sin x x0
x0 nx
x0
nx
lim sin mx / limcos x m lim sinmx /limcos x m 。
x0 nx
x0
n x0 mx x0
n
7/17
例7 求 解
lim arcsin x
x0
x
(0 型) 0
lim arcsin x yarcsin x
x0
x
lim y y0 sin y
例9 证明数列x1
3 , xn1
3 xn
的
极
限
存
在
并
求lim n
xn
.
证 易知 xn1 xn , xn是单调递增的 ;
又 x1 3 3, 假定 xk 3 xk1 3 xk 3 3 3
xn是有界的;
lim n
xn
存在.
1.
第一个重要极限
lim sin x 1 x0 x
(0 型) 0
C B
证: 设单位圆 O, 圆心角AOB x, (0 x )
2
作单位圆的切线,得AOC , 于是由
o
极限存在准则两个重要极限公式

夹逼准则不仅说明了极限存在,而且给出了求极限的
方法.下面利用它证明另一个重要的
极限公式: lim sin x 1 x0 x
证:
当
x
(
0
,
2
)
时,
BD
1x
oC
A
△AOB 的面积<圆扇形AOB的面积<△AOD的面积
即
1 2
sin
x
1 2
x
1 2
tan
x
亦故即有
1sin sxinxxxctoa1snxx
1. 单调有界准则
数列 xn : 单调增加 x1 x2 xn xn1 ,
单调减少 x1 x2 xn xn1 ,
准则I 单调有界数列必有极限 单调上升有上界数列必有极限
说 明: 单调下降有下界数列必有极限 (1) 在收敛数列的性质中曾证明:收敛的数列一定 有界,但有界的数列不一定收敛.
1
1 1 n1 n 1
1 yn1
由于数列 yn 是单调增加的,所以数列 zn 是单调减少的.
又
xn
1
1
n
n
1
1
ห้องสมุดไป่ตู้n1
n
zn
z1
4
则 2 xn 4. 综上,根据极限存在准则Ⅰ可知,数列是
收敛的.
2023年12月9日星期六
4
目录
上页
下页
返回
通常用字母 e 来表示这个极限,即
lim
n
1
1
n
)
( n 1, 2,
), 且
x1 0,
a0,
求
lim
n
xn
.
利用极限存在准则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.计算下列极限: ⑴0tan 3limx xx→;【解】这是“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 为将tan3x 化出sin3x ,利用sin 3tan 3cos3xx x=,得:0tan 3lim x x x →0sin 33lim 3cos3x x x x →=⋅313cos0=⨯=。
⑵1lim sin x x x→∞; 【解】由于1lim sin x x→∞sin 00==,这是“0⨯∞”型极限,应化为商式极限求解:1lim sin x x x →∞101sinlim1xx x→=, 这又成为了“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 101sinlim 11xx x→=,亦即1lim sin 1x x x →∞=。
⑶0lim cot x x x →;【解】由于0limcot x x →=∞,这是“0⨯∞”型极限,应化为商式极限求解:0lim cot x x x →0limtan x xx→=,这又成为了“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 同样利用sin tan cos xx x=,得: 00lim lim cos tan sin x x x x x x x→→=⋅1cos01=⨯=, 亦即0lim cot 1x x x →=。
⑷01cos 2limsin x xx x→-;【解】这是“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 为将1cos2x -化出正弦函数,利用2cos 212sin x x =-,得:01cos 2lim sin x x x x →-202sin lim sin x x x x →=0sin 2lim x xx→=212=⨯=。
⑸sin limx xxππ→-;【解】这是“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 由于不可能将x π-转化为x ,应考虑利用诱导公式,将sin x 转换为sin()x π-,得:sin limx x x ππ→-0sin()lim x x x πππ-→-=-1=。
⑹0lim x +→;【解】这是“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 为将根号去掉,并将余弦函数转化为正弦函数,可利用2cos 12sin2xx =-,得:lim x +→0limx +→=0lim sin2x x +→=0lim sin 2x x x +→=02lim sin2x x x +→=1== ⑺0sin limsin x x xx x→-+;【解】这是“”型含三角函数极限,可考虑套用极限公式()0sin ()lim1()f x f x f x →=: 0sin lim sin x x x x x →-+0sin 1lim sin 1x xx x x→-=+11011-==+。
⑻lim 2sin2nnn x→∞(x 为不等于零的常数)。
【解】由于lim sin 2n n x →∞sin 00==,知lim 2sin 2nn n x →∞属于“0⨯∞”型极限,应化为商式极限求解:lim 2sin 2n n n x →∞sin 2lim12n n n x →∞=sin 2lim 2nn nx x x →∞=⋅1x x =⨯=。
2.计算下列极限: ⑴10lim(1)xx x →-;【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:10lim(1)x x x →-1(1)0lim[1()]xx x ⨯--→=+-11lim{[1()]}x x x --→=+-1e -=。
⑵21lim()xx x x→∞+; 【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:21lim()x x x x →∞+21lim[(1)]x x x →∞=+2e =。
⑶1lim(1)kxx x→∞-(k N ∈); 【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:1lim(1)kx x x →∞-()1lim(1)x k x x -⨯-→∞=+-1lim[(1)]x k x x --→∞=+-k e -=。
⑷3lim()1x x x x+→∞+; 【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:【解法一】3lim()1x x x x +→∞+12lim()1x x x x ++→∞=+12lim()()11x x x x x x+→∞=++1(1)211lim(1)()11x x x x x+⨯--→∞-=+++ 112111lim[(1)]()111x x x x+--→∞-=+++1211e e --=⨯=。
【解法二】3lim()1x x x x +→∞+31lim()11x x x +→∞=+31lim 1(1)x x x →∞+=+31lim11(1)(1)x x x x →∞=++ 111e e -==⨯。
⑸10lim(1)x xx xe →+;【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:10lim(1)x xx xe →+1lim(1)xxe x xex xe ⋅→=+1lim[(1)]x xx e xe x xe →=+0e e e ==。
⑹lim()xx x a x a→∞+-(a R ∈). 【解】这是“1∞”型极限,可考虑套用极限公式1()()0lim [1()]f x f x f x e →+=:【解法一】lim()x x x a x a →∞+-lim()x a a x x a x a -+→∞+=-lim()()x a ax x a x a x a x a-→∞++=--222lim(1)()x a a a a x a x a x a x a-⨯→∞+=+-- 2212lim[(1)]()1x a aa a x a ax a x ax-→∞+=+--210()10a ae +=-2a e =。
【解法二】lim()x x x a x a →∞+-1lim()1x x a x a x →∞+=-(1)lim (1)xx x a x a x →∞+=-()(1)lim (1)xa a x x a aa x a x⨯→∞⨯--+=-+ [(1)]lim [(1)]xaa x x aa a x ax→∞--+=-+2a a a e e e -==。
3.已知2lim()3xx x c x c→∞+=-,求常数c . 【解】先求出2lim()xx x c x c→∞+-,这有如下两种解法:【解法一】2lim()x x x c x c →∞+-()222lim(1)x c c c c x c x c -+→∞=+-2222lim[(1)](1)x c cc c x c c x c x c-→∞=++-- 21c c e =c e =。
【解法二】由于2lim()xx x c x c →∞+-21lim()1x c c x cx c x ⨯→∞+=-+2(1)lim[](1)x c c x x c c x c x →∞+=-+21(1)lim[][(1)]xc c x x c c x c x→∞--+=-+ 2221[][]c cc e e e e-=== 即由已知得3ce =,从而知ln3c =。
4.利用极限存在准则证明: ⑴222111lim ()12n n n n n n πππ→∞+++=+++; 【证明】由于在括号内的n 个分式中,分母最大的是2n n π+,最小的是2n π+,因此这n 个分式中最小的是21n n π+,最大的是21n π+,从而有222221112n nn n n n n n n πππππ≤+++≤+++++, 可得2222222111()2n n n n n n n n n n πππππ≤+++≤+++++, 而2221lim lim 11n n n n n ππ→∞→∞==++,221lim lim 11n n n n n nππ→∞→∞==++, 即由夹逼准则得,222111lim ()12n n n n n n πππ→∞+++=+++。
证毕。
⑵01x →=。
【证明】由于0x →,故不妨设11x -<<,又因0x →的方式可以分为0x -→和0x +→, 从而可以分10x -<<和01x <<两种情况进行证明:①当10x -<<时,有011x <+<,使指数函数(1)vu x =+是减函数,于是由110n>>得到110(1)(1)(1)n x x x +<+<+,亦即11(1)1nx x +<+<, 而0lim(1)1x x -→+=,0lim 11x -→=,即由夹逼准则得,10lim (1)1nx x -→+=,亦即0lim 1x -→=; ②当01x <<时,有112x <+<,使指数函数(1)vu x =+是增函数,于是由101n<<得到101(1)(1)(1)n x x x +<+<+,亦即11(1)1nx x <+<+, 而0lim(1)1x x +→+=,0lim 11x +→=,即由夹逼准则得,10lim (1)1nx x +→+=,亦即0lim 1x +→=,综上有0lim 1x -→=,0lim 1x +→=,从而得 01x →=。
证毕。
5,…的极限存在,并求出极限。
【证明】⑴先证明数列有界:令1a =2a =3a =,…,可见n a =0n a >由于12a =<,22a =<=,…,假设12n a -<,于是,有n a =2<=,由数学归纳法知,对一切n N +∈,均成立02n a <<,可知该数列有界。
⑵再证明数列单调:由于n a =有11n n n a a a ---==2=0=>,亦即1n n a a ->必有极限。
【解】设数列的极限值为a ,对等式n a =两端求极限,得a =22a a =+,求得其正数解为2a =。
