(完整版)1极限存在准则-两个重要极限
极限存在准则与两个重要极限

极限存在准则与两个重要极限首先,我们来定义极限存在准则。
设函数f(x)在x=a的其中一去心邻域内有定义,且有极限L,那么对于任意给定的正数ε,存在正数δ,使得当0<,x-a,<δ时,有,f(x)-L,<ε。
左极限:设函数f(x)在x=a的其中一左去心邻域内有定义,且有极限L,那么对于任意给定的正数ε,存在正数δ,使得当a-δ<x<a时,有,f(x)-L,<ε。
右极限:设函数f(x)在x=a的其中一右去心邻域内有定义,且有极限L,那么对于任意给定的正数ε,存在正数δ,使得当a<x<a+δ时,有,f(x)-L,<ε。
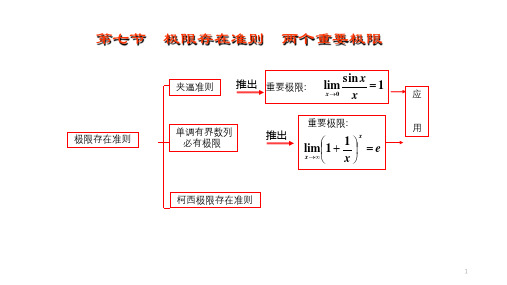
接下来,我们来介绍两个重要的极限存在准则。
1.夹逼准则(或夹挤准则):设函数f(x)在x=a的其中一去心邻域内有定义,且在这个去心邻域中,存在两个函数g(x)和h(x),满足g(x)≤f(x)≤h(x)。
若当x→a时,g(x)和h(x)的极限都是L,则函数f(x)在x=a处的极限也是L。
夹逼准则的直观意义是,如果一个函数在一些点附近被两个函数“夹住”,而这两个函数的极限是相等的,则原函数在该点也存在极限,并且极限等于夹逼的值。
2.单调有界准则:如果函数f(x)在x=a的其中一去心邻域内有定义,并且在这个去心邻域中是递增或递减的(即f’(x)≥0或f’(x)≤0),那么如果存在一个实数M,使得对于任意的x,都有f(x)≤M(或f(x)≥M),那么函数f(x)在x=a处存在极限。
单调有界准则的直观意义是,如果一个函数在一些点附近是单调递增或递减的,并且在该区间内被一个实数所界定,那么函数在该点存在极限。
这两个极限存在准则在微积分中具有重要的意义和应用。
在求解极限问题时,可以利用夹逼准则来确定极限的存在性。
而在证明一些极限存在的定理时,可以利用单调有界准则来进行证明。
总结起来,极限存在准则是用于确定函数在一些点是否存在极限的基本规则。
夹逼准则和单调有界准则是两个重要的应用极限存在准则,它们在微积分中有着广泛的应用。
两个重要的极限

例7 求 解 令 arcsin x t ,则 且 x 0时,t 0
arcsin x lim x 0 x
x sin t
arcsin x t lim lim 1 x 0 t 0 sin t x
(2)
定义
1 x lim (1 ) e x x 1 n lim (1 ) e n n
arccot x 3、 lim __________. x 0 x
4、 lim x cot 3 x __________.
x 0
sin x 5、 lim __________. x 2 x
6、 lim (1 x ) _________.
x 0
1 x
1 x 2x 7、 lim ( ) _________. x x 1 x 8、 lim (1 ) _________. x x
xn 是单调递增的 ;
1 1 1 1 xn 1 1 1 1 n 1 2! n! 2 2 1 3 n 1 3, xn 是有界的; 2 1 n lim x n 存在. 记为 lim (1 ) e (e 2.71828) n n n2例5 求 解Fra biblioteklim
x 0
tan x sin x lim x 0 x3
tan x sin x tan x(1 cos x) 1 sin x 1 cos x lim lim ( ) 3 3 2 x 0 x 0 x x cos x x x
1 sin x 1 cos x 1 (lim )( lim )( lim ) 2 x 0 cos x x 0 x 0 x 2 x
sin口 lim (口代表同样的变量 1 口0 口
极限存在准则 两个重要极限

12/19/2010 10:04 PM
1 1 1 1 2 n −1 xn = 1+ 1+ (1− ) +L+ (1− )(1− )L(1− ). 2! n n! n n n
n→∞
12/19/2010 10:04 PM
令 lim xn = A, 对递推公式
n→∞
xn = a + xn−1 的两边取极限
lim xn = lim a + xn−1 ⇒ 1 ± 1 + 4a 4a , A = a + A ⇒ A − A−a = 0⇒ A = 2
2
n→∞
n→∞
存在, 因为 xn > 0, 且 lim xn存在,则 lim xn = A ≥ 0,
类似地, 类似地,
xn +1 1 = 1 + n+1
n +1
1 1 = 1 + 1 + (1 − ) +L 2! n+1
1 1 2 n−1 )(1 − )L(1 − ) + (1 − n! n+1 n+1 n+1 1 1 2 n (1 − )(1 − )L(1 − ) + ( n + 1)! n+1 n+1 n+1
1 − cos x 1 = 1 ⋅ lim = . 2 x →0 2 x
12/19/2010 10:04 PM
sin 3 x . 例11 求 lim x →π tan 5 x 解 令x = π − t ⇒ t = π − x , 当x → π 时 ⇒ t → 0, 则 sin ( 3π − 3t ) sin 3 x lim = lim x →π tan 5 x t → 0 tan ( 5π − 5t )
两个极限存在准则和两个重要的极限

两个极限存在准则和两个重要的极限第一个极限存在准则是柯西-斯维亚切斯极限存在准则(Cauchy-Schwarz Limit Existence Criteria)。
其表述为:对于一个函数 f(x),如果对于任意的ε>0,存在一个δ>0,使得当 0<,x-a,<δ 时,总有,f(x)-f(a),<ε,则函数 f(x) 在点 a 处存在极限。
第二个极限存在准则是海涅定理(Heine's Theorem),也被称为局部有界性定理(Local Boundedness Theorem)。
其表述为:如果对于一个函数 f(x),在点 a 的一些邻域内 f(x) 有界,即存在一个常数 M>0,使得对于所有的x∈(a-δ,a+δ) 有,f(x),≤M,则函数 f(x) 在点 a 处存在极限。
这两个极限存在准则都用于判断函数在其中一点处的极限是否存在。
柯西-斯维亚切斯极限存在准则要求函数在该点的极限存在时,对于任意给定的ε>0,都能找到对应的δ>0,使得函数值与极限值的差小于ε。
而海涅定理则要求函数在该点附近有界,即函数在该点附近的函数值都不超过一些常数M。
这两个定理的应用范围和方法略有不同。
除了极限存在准则外,还有两个重要的极限:无穷小与无穷大。
无穷小是指极限趋近于零的数列或函数。
对于一个数列 {a_n},如果对于任意的正数ε>0,存在正整数 N,使得当 n>N 时,有,a_n,<ε,则该数列是无穷小。
对于一个函数 f(x),如果在其中一点 a 处,有lim(x→a) f(x)=0,则该函数在点 a 处是无穷小。
无穷大则是指极限趋于无穷的数列或函数。
对于一个数列 {a_n},如果对于任意的正数 M>0,存在正整数 N,使得当 n>N 时,有,a_n,>M,则该数列是无穷大。
对于一个函数 f(x),如果在其中一点 a 处,有lim(x→a) f(x)=∞(或表示为lim(x→a) ,f(x),=∞),则该函数在点 a 处是无穷大。
极限存在准则 两个重要极限

第二个重要极限:勇气极限
勇气极限是指我们所能承受的恐惧和心理压力的极 限。了解并逐步超越这个极限,可以使我们在挑战 中变得无所畏惧。
重要性说明
1 激发潜力
了解重要极限能激发我们 内在的潜力,鼓励我们尝 试新事物并突破自身的局 限。
2 规避风险
重要极限的认识有助于我 们规避风险,避免陷入危 险和不理智的决策中。
极限存在准则:两个重要 极限
在极限存在的世界里,我们要探讨两个重要极限:极限存在准则以及第一个 和第二个重要极限。让我们一同揭开生活中最极致的部分。
极限存在准则
1
什么是极限存在准则?
极限存在准则是指在一定条件下,存在着极限情况的规律和约束。它定义了事物 的极限状态和行为。
2
为什么极限存在准则重要?
3 追求卓越
超越重要极限是追求卓越 的关键一步,让我们不断 学习、成长和创新。
实际应用
运动训练
运动训练中,了解和超越个人身体极限是提高 体能和成绩的关键。
领导能力
领导者需要超越自身能力和局限,带领团队不 断创新和突破。
创业企业
创业企业需要超越市场的竞争和资源限制,寻 找新的商业机会和创新解决方案。
科学研究
科学研究需要不断突破知识和技术的边界,发 现未知领域和新的发现。
总结和结论
极限存在准则以及两个重要极限的认识,可以帮助我们更好地理解和应对生活中的极端情况和挑战。通过超越 这些极限,我们能够实现更高的成就和创造。
极限存在准则能帮助我们了解事物的极端表现和局限,提醒我们在决策和行动中 要注意避免超越这些极限。
3
应用领域
极限存在准则广泛应用于科学研究、工程设计、金融市场和人类行为等领域,在 寻找平衡和解决问题时发挥着关键作用。
第六节两个重要极限

x
x
lim(1 1 )x e
x
x
8/18/2019 3:32 PM
第二章 极限与连续
若在极限 lim(1 1 )x e 中,令 t 1
x
x
x
得极限的另一种形式
1
lim(1 t)t e
t0
这种数学模型在实际中非常有用,例如 “银行计算复利问题”。设本金为 A0,利率为 r , 期数为 t ,如果每期结算一次,则本利和 A为
lim x A
证毕。
例1 证明 limsin x 0 x0
证 当 x 时,0 sin x x
2
由 lim x 0 , x0
再根据准则1,得
limsin x 0 证毕。
x0
8/18/2019 3:32 PM
第二章 极限与连续
例2 证明 limcos x 1 x0
2
8/18/2019 3:32 PM
第二章 极限与连续
1 x 1
(0 x )
sin x cos x
2
sin x是偶函数
x
得到 cos x sin x 1 (0 x )
x
2
limcos x 1 , lim sin x 1
x0
x0 x
证毕。
例4
计算 lim tan x
8/18/2019 3:32 PM
第二章 极限与连续
而
lim(1
n
n
1
)n 1
lim
n
(1 n
1
1 )n1 1 1
e
n1
lim(1 1 )n1 lim(1 1 )n(1 1 ) e
高等数学 第1章 第七节 极限存在准则 两个重要极限
则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,(舍去)
lim n
xn
3.
14
3.两个重要极限的应用
例6: 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解: lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知:
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明:
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x
极限存在准则两个重要极限公式

夹逼准则不仅说明了极限存在,而且给出了求极限的
方法.下面利用它证明另一个重要的
极限公式: lim sin x 1 x0 x
证:
当
x
(
0
,
2
)
时,
BD
1x
oC
A
△AOB 的面积<圆扇形AOB的面积<△AOD的面积
即
1 2
sin
x
1 2
x
1 2
tan
x
亦故即有
1sin sxinxxxctoa1snxx
1. 单调有界准则
数列 xn : 单调增加 x1 x2 xn xn1 ,
单调减少 x1 x2 xn xn1 ,
准则I 单调有界数列必有极限 单调上升有上界数列必有极限
说 明: 单调下降有下界数列必有极限 (1) 在收敛数列的性质中曾证明:收敛的数列一定 有界,但有界的数列不一定收敛.
1
1 1 n1 n 1
1 yn1
由于数列 yn 是单调增加的,所以数列 zn 是单调减少的.
又
xn
1
1
n
n
1
1
ห้องสมุดไป่ตู้n1
n
zn
z1
4
则 2 xn 4. 综上,根据极限存在准则Ⅰ可知,数列是
收敛的.
2023年12月9日星期六
4
目录
上页
下页
返回
通常用字母 e 来表示这个极限,即
lim
n
1
1
n
)
( n 1, 2,
), 且
x1 0,
a0,
求
lim
n
xn
.
利用极限存在准则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Afr .-f-e
第一早第八节
极限存在准则两个重要极限
【教学目的】
1、 了解函数和数列的极限存在准则;
2、 掌握两个常用的不等式;
3、 会用两个重要极限求极限。
【教学内容】
1、 夹逼准则;
2、 单调有界准则;
3、 两个重要极限。
【重点难点】
重点是应用两个重要极限求极限。
难点是应用函数和数列的极限存在准则证明极限存在,并求极限。
【教学设计】 从有限到无穷,从已知到未知,引入新知识( 3分钟)。
首先给出极限存在准
则(10分钟),并举例说明如何应用准则求极限(
5分钟);然后重点讲解两个重要的极限类
型,并要求学生能利用这两个重要极限求极限( 10分钟);课堂练习(5分钟)。
【授课内容】
引入:考虑下面几个数列的极限
1000
3、lim X n ,其中 x n = 、.、3+ x n-1, N = '、3,极限不能确定。
对于2、3就需要用新知识来解决,下面我们来介绍极限存在的两个准则:
一、极限存在准则
1. 夹逼准则
准则I 如果数列X n ,y n 及Z n 满足下列条件
(1) y n X n Z n (n 1,2,3 )
(2) lim y n
a, lim z n a,
n
n
那么数列X n 的极限存在,且lim X n
a .
n
证: y a, z a,
0, N 1 0, N 2 0,使得
1、 lim
n
n 2
1000个0相加,极限等于 0。
2、 lim
n
——2一无穷多个
.n i
0”相加,极限不能确定。
当n N1时恒有y n a ,当n N2时恒有Z n
取N 二max{N j , N 2},上两式同时成立,即a _1_ n 2 2
【说明】 夹逼准则应恰当结合“放缩法”使用
2. 单调有界准则
准则n 单调有界数列必有极限
几何解释:
X 2 X 3 X n X
n 1
A
1 - 3—X n , X 1 ,3,求lim X n 。
首先证明是有界的,然后证明是单
n
调的,从而得出结论
证:1、证明极限存在
例2证明数列
X n
.3 '/L 3 ( n 重根式)的极限存在
当n > N 时,恒有 a
y n x n z n a ,即 X n a
成立, lim x n a.
n
上述数列极限存在的准则可以推广到函数的极限
o
准则I '如果当X U (x 0,)(或x M )时,有
(1) g(x) f(x) h(x),
⑵』m g(x) A ,』m h(x) A,
x x
x x
(x ) (x )
那么lim f (x)存在,且等于A .
x x 0 (x )
准则 和准则'称为夹逼准则。
【注意】利用夹逼准则求极限的关键是构造出
y n 与z n ,并且y n 与z n 的极限是容易求的。
解:
又lim
n
1
1 求 lim(
+
=+ L n
“n 2+ 1
、n 2 + 2
+
J 2
:
).
.n + n
1 + . < ..n
2 + n
lim
n
1,
lim 一n -
n
lim
n
1, 1
2
y n a 由夹逼定理得:
-)1- n
如果数列x n 满足条件X 1 加的;如果数列 x n
满足条件X 1 x 2 x 3 少的。
单调增加和单调减少的数列统称为单调数列。
X 2 X 3 X n X n
X n 1 X n 1
,就称数列 x n 是单调增 ,就称数列x n 是单调减
【分析】已知X n
2
2
(|)2
2
(1
a )证明有上界
N 3 3,设 x n
3 x
n 1
3
, 则 X n 1 ,3 X n 3一3 3
所以对任意的n 有 X n
3
b )证明单调上升
X n 1 X n ... 3 X n X n
X n X n
X n x n
x n
所以lim X n 存在
n
2、求极限 设 lim x n
l n
,则I .FT ,解得I
卫舍去)
所以 lim x n n
两个重要极限
1. sin x ’ lim
1 x 0 x
如右图所示,设单位圆O,圆心角 AOB X,
(0 X 2)
作单位圆的切线, 得ACO.扇形OAB 的圆心角为x, OAB 的高为BD, 于是有sinx BD, x 弧AB,
tanx AC,
sin x x tan x, 即 COSX 沁1,上式对于
- x 2 2时,° cosx 1 1 cosx 2 sin 2 △
2(52
X 0也成立. 2
lim — x 0 2 0, lim (1 cosx) x 0
0, lim cosx x 0
1,又
lim1 x 0
1,
lim
sin X
x 0
(1) 求下列极限
1- cosx lim 2— x ?0 x 2 解:原极限=lim 0 X? 2
X 2sin
— 2
2
X
2x
m
1.
sin 2^ x
sin
2凹(二
2. lim (1 丄广
x
x
,lim 0(1
x 0
1
x)x e , lim n
“1 ”型
X
【说明】
1
(1)
上述三种形式也可统一为模型
lim 1 x 一冈 e
(x) 0
(2) 第二个重要极限解决的对象是
1型未定式。
2
例如,lim 2 x 门 lim 1
X 1
X 1
(2) lim
X
而广 n(n 1) 2
1
n(n 1)/2 1 而 lim 2
, lim 厂 n
n
n n 2 n n n 1
2
1 所以原极限 一 2
【内容小结】
lim f (x) A = lim h(x),则 lim g(x) A 。
X X o
XX)
x X o
2、单调有界准则
(1) 单调上升有上界的数列,极限一定存在;
解:
n 2n
n 1) 2
1 2 n
2 n n
n n 2 n n n 2 n n n 1
2
L
n
2 n n 1 2 n n 2
2 n n n
1
2
L
n n(n 1) 2 2 n n
1 2 n n 1 2 n n 1 2 n n 1
O
i 1
【课堂练习】求lim
n
n (1) 求下列极限
x
lim(1 -
X
解:原极限二 lim[(1
X
X ) x
]
lim
X
(1
解:原极限=lim[(1
X
")
1、夹逼准则
o
当 X U(X 0,)时
有 f (X) g(x) h(x)
(2) 单调下降有下界的数列,极限一定存在。
3、两个重要极限
(X 为弧度);
1
1 x 一
(2) lim (1
)x e , lim (1 x)x e x
x x 0
mo
z
\1。
