第五章 固体电子论基础2
合集下载
固体物理-第五章--固体电子论基础1

d2 dx 2
d2 dy2
d2 dz 2
布洛赫、布里渊等人利用势场的周期性
[V(x)=V(x+nx)]和微扰理论,计算出了晶体中电子的能 带和禁带分布,解释了晶体中导体和绝缘体存在的原因,
并从理论上预言了半导体的存在。 16
§5.1 电子气的能量状态 一、一维晶体中电子气的能量分布
1.量子力学(索末菲)自由电子模型 (1)电子之间相作用很弱,完全忽略。电子只有动能, 没有相互作用势能。 (2)电子和离子实之间的相互作用可看成是电子在离子 实的平均势场中运动, V(x)=V0。 (3)把电子看成是服从费米-狄拉克分布的、封闭于晶体 中的理想气体(自由电子气)。
第五章 固体电子论基础
1
一、经典理论对电子气的描述
1.特鲁特自由电子模型(1900年) (1)金属中的价电子象气体分子一样组成电子气,在温 度为T的晶体内,它们的行为和理想气体中的气体分子 一样。 (2)除了和金属离子碰撞以外,基本上是自由的。通过 和金属离子的碰撞在一定温度下达到热平衡。可以用具 有确定的平均速度和平均的自由时间的电子来代表。 (3)在外电场的作用下,电子气产生的漂移运动引起了 电流。
1x2 y3 z
26
(3)化简
(4)通解
d
2 1x
d x2
k
2
x1
x
0
d
2 2
d y2
y
k
y2
2
y
0
d
2 3 z
d z2
kz2 3
z
《固体电子论基础》课件

课件的编写目的和意义
课件的结构和内容安排
课件目的
掌握固体电子论的基本概念和原理 了解固体电子论在材料科学中的应用 掌握固体电子论的数学基础 了解固体电子论在物理、化学等领域的应用
适用人群
固体电子论专业本 科生
固体电子论爱好者
电子工程、材料科 学等领域的研究人 员
对固体电子论感兴 趣的其他人员
课件结构
固体电子论在器 件设计中的应用
半导体技术 太阳能电池 电子器件 磁学和光学应用
应用领域
固体电子结构与性质
固体电子结构
固体电子论的 概述
固体电子的能 级结构
固体电子的态 密度
固体电子的输 运性质
电子性质
电子的电荷与质 量
电子的能级与跃 迁
电子的波粒二象 性
电子在固体中的 行为
固体能带结构的定义
固体电子论概述
固体电子论的定义
定义与概念
固体电子论的研究对象
固体电子论的基本概念
固体电子论与量子力学、固体物理学的关系
固体电子论的起源
发展历程
固体电子论的发展阶段
固体电子论的应用领域
固体电子论的未来展望
研究内容
固体电子论的基 本概念和原理
固体电子论的研 究对象和方法
固体电子论在材 料科学中的应用
单击此处输入你的 项正文
电流方向:单向 导电
单击此处输入你的 项正文
伏安特性:正向和 反向伏安特调幅 信号解调为音频信
号
单击此处输入你的
项正文
开关电路:控制 电路的通断
单击此处输入你的 项正文
晶体管工作原理及应用
晶体管基本结构与工作原理 晶体管类型与特性 晶体管在电路中的应用 晶体管在固体电子器件中的重要性
固体物理 第五章 固体电子论基础2(2)
d u du 2 2 可得: + ik 2 -k u 0 2 dx dx
2
4
(2)特征方程为:
2
r 2ikr -k 0
2 2
r
- ik 2
2ik -4 -k -ik i
2 2 2
r1 -i k ,r2 i -k
i -k e
i -k c
= -ik e
A0 i k e -
-i k c
- -ik b
C 0 ik e -
B0 D0
ik b
(4)
16
(3)方程组
A0 B0 C 0 D0 0 - - = = i -k A0 - i k B0 - -ik C 0 + ik D0 0 i -k c e A0 e-i k c B0 - e - -ik bC 0 - e ik b D0 0 = i -k e i -k c A0 i k e-i k c B0 -ik e - -ik bC 0 - - ik e ik b D = + 0 0
2.波函数和薛定谔方程 (1)波函数 根据布罗赫定理可得:
x e ikxux
(2)薛定谔方程 把波函数代入薛定谔方程可得:
2 d 2 V x ψ x Eψ x 2 2m dx
d 2 2m + 2 E - V 0 2 dx
Dne
u x 是周期函数
u x u x na
C0e
-ik x
D0e
e
- ik x
C ne
固体物理:第五章 晶体中电子能带理论

电子在一个具有晶格周期性的势场中运动
V r V
r
Rn
其中 Rn 为任意格点的位矢。
2 2 2m
V r
E
2. 布洛赫定理
当势场具有晶格周期性时,波动方程的解具有如下性质:
(
r
Rn
)
eikRn
(
r
),
其中 k
为电子波矢,Rn
n1 a1 n2 a2 n3 a3
是格矢。
个能级分裂成N个相距很近的能级, 形成一个准连续的能带。 N个原子继续靠近,次外壳层电子也开始相互反应,能级 分裂成能带。
能带理论
能带论是目前研究固体中的电子状态,说明固体性质最重 要的理论基础。
能带理论是用量子力学的方法研究固体内部电子运动的理 论。它曾经定性地阐明了晶体运动的普遍特点,并进而说 明了绝缘体与半导体、导体的区别所在,解释了晶体中电 子的平均自由程问题。
原子中的电子处在不同的能级上,形成电子壳层
原子逐渐靠近,外层轨道发生电子的共有化运动——能级分裂
原子外壳层交叠的程度最大,共有化运动显著,能级分裂的很厉害, 能带很宽;
原子内壳层交叠的程度小,共有化运动很弱,能级分裂的很小,能 带很窄。
N个原子相距很远时,相互作用忽略不计。 N个原子逐渐靠近,最外层电子首先发生共有化运动,每
第五章 晶体中电子 能带理论
表征、计算和实验观测电子结构是固体物理学的核心问题; 这是因为原则上研究电子结构往往是进一步解释或预言许 多其他物理性质的必要步骤。
晶体电子结构的内涵是电子的能级以及它们在实空间和动 量空间中的分布。
玻尔的原子理论给出这样的原子图像:电子在一些特定的可能轨道 上绕核作圆周运动,离核愈远能量愈高,当电子在这些可能的轨道 上运动时原子不发射也不吸收能量,只有当电子从一个轨道跃迁到 另一个轨道时原子才发射或吸收能量,而且发射或吸收的辐射是单 频的。
沈阳工业大学《固体物理》(李新)第五章

第五章固体电子论基础物理现象或实验结果物理模型决定因素理论解释第一阶段自由电子学说德鲁特和洛伦兹第二阶段量子自由电子学说fs电子理论第三阶段能带理论单电子近似求解电子能谱的理论固体电子论基础电子在运动中存在一定的散射机制
第五章 固体电子论基础
固体电子论基础 决定因素
修 改
物理现象 或实验结果
物理模型
v e
x
1 2 ( mv x ) / kT 2
dvx
m 2kT kT E0 / kT 2e( ) 3 e EF / kT e AT 2 e / kT h m m
此即里查孙-杜师曼公式;其中即功函数 因为
j 1 ln 2 ln A k T T
2 E0 m
2m dZ 4Vc 2 h
3/ 2
2m dE dk 2 E
3/ 2
E 1 / 2 dE
3/ 2
能态密度为:
dZ 2m N E 4Vc 2 dE h
E 1 / 2 CE1 / 2
2m C 4Vc 2 h
每个量子态k在波矢空间体积:
2 2 2 2 L L L L
3
k 空间中的状态分布
3
单位体积中的量子态数为:
L 2
1 .索末菲自由电子论
1.2运动方程及其解 在能量E到E+dE之间的区域,是半径为k到k+dk两个球面
之间的球壳层,它的体积为:
理论解释
验 证
结果与预言
第一阶段、自由电子学说-德鲁特和洛伦兹 第二阶段、量子自由电子学说-F-S电子理论 第三阶段、能带理论-单电子近似求解电子能谱的理论
第五章 固体电子论基础
固体电子论基础 决定因素
修 改
物理现象 或实验结果
物理模型
v e
x
1 2 ( mv x ) / kT 2
dvx
m 2kT kT E0 / kT 2e( ) 3 e EF / kT e AT 2 e / kT h m m
此即里查孙-杜师曼公式;其中即功函数 因为
j 1 ln 2 ln A k T T
2 E0 m
2m dZ 4Vc 2 h
3/ 2
2m dE dk 2 E
3/ 2
E 1 / 2 dE
3/ 2
能态密度为:
dZ 2m N E 4Vc 2 dE h
E 1 / 2 CE1 / 2
2m C 4Vc 2 h
每个量子态k在波矢空间体积:
2 2 2 2 L L L L
3
k 空间中的状态分布
3
单位体积中的量子态数为:
L 2
1 .索末菲自由电子论
1.2运动方程及其解 在能量E到E+dE之间的区域,是半径为k到k+dk两个球面
之间的球壳层,它的体积为:
理论解释
验 证
结果与预言
第一阶段、自由电子学说-德鲁特和洛伦兹 第二阶段、量子自由电子学说-F-S电子理论 第三阶段、能带理论-单电子近似求解电子能谱的理论
固体物理-第五章晶体中电子能带理论2-PPT精品文档

'Vne a
n
由 H ˆk(x)kk(x)得
EkEk(0)Ek(1)Ek(2)
k(x)k(0)(x)k(1)(x)k2)(x)
零
H ˆ0 k(0)(x) k(0)(x)
级 近 似 解
k(0)(x)
1
eikx ;
L
(0) k
2k 2 2m
a
0 其他情况
k VkL1e-ik x 0L
i2πn x
'V nea
n
1eik xd x L
k 2 l,k 2 l
Na Na
二级微扰能量:
i2πnx
V 'Vne a
n
k' Vk 2
(0)
k
/
k
(0) (0)
k
k
H (r) 2m 2 2Vr (r)(r)
的本征函数是按布拉维格子周期性调幅的平面波,即
k(r)eikruk(r)且 ukruk rRn
对 R n 取布拉维格子的所有格矢成立。 R n n 1 a 1 n 2 a 2 n 3 a 3
上述讨论没有涉及周期性势场V ( r ) 的具体形式,是普遍性
k 2π
把波函数 (r) k
1 eikr V
2
代回薛定谔方程 2(r)(r)
2m
得到电子的本征能量为:
2k 2 2m
2m 2 (kx2k2y kz2)
电子的动量:
电子处在
k
(r
)
1 eikr V
时,有确定的动量:
p k
电子的速度:
v p k mm
n
由 H ˆk(x)kk(x)得
EkEk(0)Ek(1)Ek(2)
k(x)k(0)(x)k(1)(x)k2)(x)
零
H ˆ0 k(0)(x) k(0)(x)
级 近 似 解
k(0)(x)
1
eikx ;
L
(0) k
2k 2 2m
a
0 其他情况
k VkL1e-ik x 0L
i2πn x
'V nea
n
1eik xd x L
k 2 l,k 2 l
Na Na
二级微扰能量:
i2πnx
V 'Vne a
n
k' Vk 2
(0)
k
/
k
(0) (0)
k
k
H (r) 2m 2 2Vr (r)(r)
的本征函数是按布拉维格子周期性调幅的平面波,即
k(r)eikruk(r)且 ukruk rRn
对 R n 取布拉维格子的所有格矢成立。 R n n 1 a 1 n 2 a 2 n 3 a 3
上述讨论没有涉及周期性势场V ( r ) 的具体形式,是普遍性
k 2π
把波函数 (r) k
1 eikr V
2
代回薛定谔方程 2(r)(r)
2m
得到电子的本征能量为:
2k 2 2m
2m 2 (kx2k2y kz2)
电子的动量:
电子处在
k
(r
)
1 eikr V
时,有确定的动量:
p k
电子的速度:
v p k mm
《固体物理学》房晓勇主编教材课件-第五章 金属电子论基础

海南大学
第
教学要求、重点
教学要求:
掌握金属自由电子气体模型。
海 掌握电子比热的量子理论。
大
了解逸出功和接触电势差。 纳 了解电场中的自由电子、光学性质、金属电子组率、霍耳效应 道
百
和金属热导率。
致
川
教学重点:
远
费密能、热容量、接触电势差、电子与声子的相互作
用、金属电导率
教学难点:
玻耳兹曼方程、弛豫时间的统计理论、纯金属电阻率
大
纳
经典自由电子气体理论的基础是自由电子气体模型,即 道
百 金属电子气体假定,它包括二层基本含意;
致
川
(1)忽略电子与离子实之间的相互作用,且因为存在表
面势垒,电子自由运动的范围仅限于样品内部。在金属中, 远
由于带正电的离子实均匀分布,施加在电子上的电场零.因
此对电子并没有作用。这一假定称为自由电子近似。
成自由电子气,称为金属电子气。是特鲁特(P.Drude)1900
这些自白电子可以同金属中离
海 年提出的,称为特鲁特模型。
大
海 子实碰幢,在一定温度下达到热
大
纳
道
纳 平衡状态。按照特鲁特模型,金 属中酌电子气体可以用具有确定
道
百
致
百 的平均速度和平均自由时间的电
致
川
远
川 子运动来描述。 例如,在外电
远
nx
( nx
=
0, ±1, ±2,⋅⋅⋅)
(1)
所以两个分立值之间的距离为2Л/L,因此单位长度允
许的状态数目为L/ 2Л 。
海南大学
4
第
而在dk范围内容纳的状态数为
dZ = L dk (2)
《固体物理学》房晓勇主编教材-思考题解答参考05第五章 金属电子论基础

T →0
5.8 什么是逸出功?在热电子发射问题中,逸出功与那些因素有关? 解答:将电子离开金属表面至少需要从外界得到的能量称为逸出功。 逸出功跟温度和晶体表面特性(如点整结构、杂质吸附等)有关。 5.9 什么是热电子效应?它是怎样形成的?当金属表面附近施加一高强度电场时,对热电子发射有何 影响? 解答:在 T = 0 时,所有电子能量不超过费米能量 EF ,因此没有电子脱离金属;但是,当金属被加 热到很高温度时,将有一部分电子获得的能量大于逸出功,从而脱离金属表面形成热电子发射电流,这种 现象称为热电子效应。 5.10 产生接触电势差的原因是什么? 解答:当两块不同的金属 1 和 2 相接触, 或用导线连接时, 两块金属将彼此带电并产生不同的电势 U1 和 U 2 ,称为接触电势差。 接触电势差来源于两块金属的费米 能级不一样高。由于两块金属具有不同 的费米能级 EF 1 和 EF 2 ,所以当两块金 属接触时,电子从费米能级较高的金属 1 流到费米能级较低的金属 2, 而接触电 势差正好补偿了两块金属的费米能级差
(4)根据《固体物理学》式 5-17 和式 5-19,与费米能级对应的能态密度
1 ⎛ 2m ⎞ g (E) = ⎜ ⎟ 2π 2 ⎝ = 2 ⎠
3/ 2
E
1/ 2
1 ⎛ 2m ⎞ = ⎜ ⎟ 2π 2 ⎝ = 2 ⎠
3/ 2
2 ⎛ = 2kF ⎞ ⎜ ⎟ ⎝ 2m ⎠
1/ 2
=
m k π 2= 2 F
G
G′
ρl ∝ n ( q ) Δp
因为 Δp ∝ T , n ( q ) ∝ T
2
3
所以 ρ l ∝ T 5 5.7 简述化学势的意义,它与费米能级满足什么样的关系。 解答:化学势的意义是:在体积不变的条件下,系统没增加一个电子所需要的自由能。在温度接近于
5.8 什么是逸出功?在热电子发射问题中,逸出功与那些因素有关? 解答:将电子离开金属表面至少需要从外界得到的能量称为逸出功。 逸出功跟温度和晶体表面特性(如点整结构、杂质吸附等)有关。 5.9 什么是热电子效应?它是怎样形成的?当金属表面附近施加一高强度电场时,对热电子发射有何 影响? 解答:在 T = 0 时,所有电子能量不超过费米能量 EF ,因此没有电子脱离金属;但是,当金属被加 热到很高温度时,将有一部分电子获得的能量大于逸出功,从而脱离金属表面形成热电子发射电流,这种 现象称为热电子效应。 5.10 产生接触电势差的原因是什么? 解答:当两块不同的金属 1 和 2 相接触, 或用导线连接时, 两块金属将彼此带电并产生不同的电势 U1 和 U 2 ,称为接触电势差。 接触电势差来源于两块金属的费米 能级不一样高。由于两块金属具有不同 的费米能级 EF 1 和 EF 2 ,所以当两块金 属接触时,电子从费米能级较高的金属 1 流到费米能级较低的金属 2, 而接触电 势差正好补偿了两块金属的费米能级差
(4)根据《固体物理学》式 5-17 和式 5-19,与费米能级对应的能态密度
1 ⎛ 2m ⎞ g (E) = ⎜ ⎟ 2π 2 ⎝ = 2 ⎠
3/ 2
E
1/ 2
1 ⎛ 2m ⎞ = ⎜ ⎟ 2π 2 ⎝ = 2 ⎠
3/ 2
2 ⎛ = 2kF ⎞ ⎜ ⎟ ⎝ 2m ⎠
1/ 2
=
m k π 2= 2 F
G
G′
ρl ∝ n ( q ) Δp
因为 Δp ∝ T , n ( q ) ∝ T
2
3
所以 ρ l ∝ T 5 5.7 简述化学势的意义,它与费米能级满足什么样的关系。 解答:化学势的意义是:在体积不变的条件下,系统没增加一个电子所需要的自由能。在温度接近于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ψ k ( x ) e ikx uk ( x ) uk ( x ) uk ( x+na )
具有如此形式的波函 数称为布洛赫函数.
8
5.布罗赫定理证明
(1)Ĥ算符的周期性证明
d2 d2 和 2 作用效果相同, 2 dx d x a
ˆ ˆ ˆˆ ˆ H x H x a TH x H x a H x =ˆ
(3)波函数及其一阶导数在势场突变点必须连续。
x 、 x 连续
u x 、u x 连续。
19
二、求解波函数
1.在0<x<c区域,势能V=0
(1)薛定谔方程
V x
2mE 令 2 2 代入薛定谔方程
V0
-a
-b 0
c a
d 2u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
其它电子的运动。即所有电子的运动都是关联的。
平均场近似—用一种平均场来代替电子之间的相互
作用„利用Hartree(哈特里) —Fock(福克)自洽场方法‟, 即假定每个电子所处的势场都相同。 将多电子问题简化为单电子问题,每个电子是在固 定的离子势场以及其它电子组成的平均场中运动。所有 的电子都满足同样的薛定谔方程。
服从费米—狄拉克分布。
3
2.布里渊模型—晶体中势场的周期性
金属中正离子形成的电场是一种周期性变化的电场。
电子接近正离子时其势能要降低,离开正离子时期势能
要升高。电子在金属中的运动并不是完全自由的。
晶体中所有的正离子势场和其它电子的平均场是周
期性势场。电子是在规则排列的周期性势场中运动。这 种势场具有晶格的周期性。 对于一维势场: V(x)=V(x+na)
V r V r Rn
4.布罗赫定理 (1)布罗赫定理 在周期性势场V(x)中运动的电子,其能量E(k)和波 函数 k(x)必须满足薛定谔方程,波函数是按晶格周期
调幅的平面波。
(2)布罗赫定理的数学表达式
2 d 2 - +V x ψ k ( x ) E k ψ k ( x ) 2 2m dx
§5.5 布洛赫波
固体电子论—主要研究固体中电子的运动规律。 固体中电子的运动状态对固体的力学、热学、电 磁学、光学等物理性质有着非常重要的影响。因此研
究固体中电子运动规律是固体物理学的一个重要内容。 固体电子论主要包括 1.经典自由电子论(特鲁特-洛伦兹模型); 2.量子力学自由电子理论(索末菲模型); 3.能带理论(布里渊模型)。
k K h x 也是波函数的解。
12
(8)波函数表达式
k x Ahe i k K
u x Ahe
h h iK h x
h
x
e ikx Ahe iK h x e ikxu x
h
(9)u(x)的周期性
u x na Ahe
h
1 2
一个本征值可以和无数 个波矢k、k K 1、k K 2 对应。
3.k的取值范围 为了保证k的取值和本征值一一对应,把k的取值限
制在倒格子的原胞之内。如图红线区域所示。
2 l - k ,k a a Na
N N - l 2 2
波矢k的取值范围称为简约布里渊区(或第一布里渊 区), 其中的波矢称为简约波矢, 共有N个(N是原胞数)。
在K空间, Kh表示倒格点的分布。
2h 2 4 6 Kh , h 0,1,2,。K 1 , K2 , K3 a a a a
K1
4 3 2 a a a
K2
2 a 3 a 4 a
a
O
a
k
2. k x 和 k+K h x 的等同性
单电子近似的理论—把每个电子的运动看成是独立的在 一个等效势场中的运动。
2
一、布洛赫定理
1.不同自由电子模型中的势场分布
(1)特鲁特-洛伦兹模型
忽略晶体的势场。自由电子服从麦克斯韦—玻耳
兹曼分布。 (2)索末菲模型 平均势场,V0 =常数(可选V0=0)。自由电子服从 费米—狄拉克分布。 (3)布里渊模型 周期性势场,势场分布具有晶格的周期性。电子
h
iK h x na
e
iK h na
A e
h h
iK h x
e
i
2h na a
Ahe
h
iK h x
Ahe
h
iK h x
u x
结论:在周期场中运动的粒子的波函数是布洛赫函数。
即调幅的的平面波,调幅函数具有晶体的周期性。
13
二、波矢k的取值范围
1.倒格矢Kh的物理意义
6
(3)周期场近似
周期场近似,所有离子势场和
其它电子的平均场是周期性势场。 (4)单电子近似 将电子气在晶体中运动的多粒子的多体问题近似的 简化为一个电子在周期性势场中运动的问题来处理的方 法称为单电子近似。建立在单电子近似基础上的固体理 论称为能带理论。 (5)近自由电子模型 如果晶体中电子的势能同系统中电子能量的平均值 相比是一个微小量, 可在自由电子模型的基础上作微扰 计算。这种模型称为近自由电子模型。 7
论电子问题时,可以认为离子实是固定在瞬时位置上不 动。电子是在固定不动的离子实产生的势场中运动。晶
格振动以及其它缺陷对电子的影响可以用微扰方法处理。 通过绝热近似, 电子问题。 把多种粒子的多体问题简化为了多
5
(2)平均场近似
由于任何一个电子的运动不仅与它自身的位置有关,
而且还与所有其它电子的位置有关,并且该电子也影响
d u du 2 2 可得: + ik 2 -k u 0 2 dx dx
2
20
(2)特征方程为:
2
r 2ikr -k 0
2 2
r
- ik 2
2ik -4 -k -ik i
2 2 2
r1 -i k ,r2 i -k
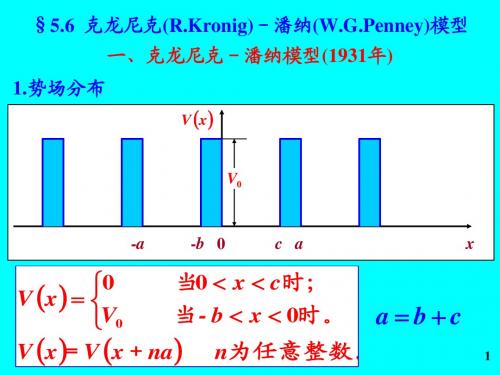
V x V x+na =
abc
17
n为任意整数。
2.波函数和薛定谔方程 (1)波函数 根据布罗赫定理可得:
x e ikxux
(2)薛定谔方程 把波函数代入薛定谔方程可得:
2 d 2 V x ψ x Eψ x 2 2m dx
ˆ n x n x T
10
(5)利用波恩-卡门边界条件求出本征值
x+Na x
ˆ N x N x x+Na x T
1, =e 令
N
ika
e
N
ikNa
1
Nka 2l. l 0,1,2,
d 2 2m + 2 E - V 0 2 dx
18
d 2m + 2 E - V 0 2 dx
2
x e ikxux
d 2u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
2 k l. l 0,1,2, Na
ˆ x e ika x T k k
11
(6)本征函数的形式
本征函数 x 如具有 x e ikx的形式,则满足本征方 程。
ˆ x e ika x T k k
ˆ x x+a e ik x a e ika e ikx e ika x T
1
能带理论 是研究固体中电子运动的主要理论基础,能带理论 定性地阐明了晶体中电子运动的普遍性及其特点,说明 了导体、非导体的区别。能带理论提供了分析半导体理 论问题的基础,推动了半导体技术的发展。 随着计算机技术的发展,能带理论的研究从定性
的对普遍性规律的研究发展到对具体材料复杂能带结构
的计算。
能带理论—是建立在单电子近似基础上的固体理论。
(7)波矢的周期性
ˆ T k K h x k K h x+a e i k K h x a e i k K h a e i k K h x
2h Kh h为整数。 a
e ika k K h x k K h x
ika ˆ x e ika x ,T ˆ T k k K h x e k K h x k
14
x 和 k K 有相同的本征值: ika。即 k e k x 、 k K 、 k K 、 都具有相同的本征值。 也即
(3)薛定谔方程的解
2
u x A0e i -k x B0e-i k x A0、B0为任意常数。
21
2.在-b<x<0区域,势能为V0,且E< V0
(1)薛定谔方程
V x
2m 令 = 2 V0 E - 2mV 0 = 2 - 2
2
V0
代入薛定谔方程
ˆ ˆ 2T和H对易性证明
ˆˆ ˆ ˆ ˆ TH x x H x a x a H x T x
ˆ ˆ T和H对易, 所以它们具有共同的本 征函数。
9
ˆ 3T的性质
ˆ Tf x f x a
f x 为任意函数;
15
4.波函数示意图
势能
波函数 实数部分
ux 因子
平面波 实数部分 16
§5.6 克龙尼克(R.Kronig)-潘纳(W.G.Penney)模型 一、克龙尼克-潘纳模型(1931年)
具有如此形式的波函 数称为布洛赫函数.
8
5.布罗赫定理证明
(1)Ĥ算符的周期性证明
d2 d2 和 2 作用效果相同, 2 dx d x a
ˆ ˆ ˆˆ ˆ H x H x a TH x H x a H x =ˆ
(3)波函数及其一阶导数在势场突变点必须连续。
x 、 x 连续
u x 、u x 连续。
19
二、求解波函数
1.在0<x<c区域,势能V=0
(1)薛定谔方程
V x
2mE 令 2 2 代入薛定谔方程
V0
-a
-b 0
c a
d 2u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
其它电子的运动。即所有电子的运动都是关联的。
平均场近似—用一种平均场来代替电子之间的相互
作用„利用Hartree(哈特里) —Fock(福克)自洽场方法‟, 即假定每个电子所处的势场都相同。 将多电子问题简化为单电子问题,每个电子是在固 定的离子势场以及其它电子组成的平均场中运动。所有 的电子都满足同样的薛定谔方程。
服从费米—狄拉克分布。
3
2.布里渊模型—晶体中势场的周期性
金属中正离子形成的电场是一种周期性变化的电场。
电子接近正离子时其势能要降低,离开正离子时期势能
要升高。电子在金属中的运动并不是完全自由的。
晶体中所有的正离子势场和其它电子的平均场是周
期性势场。电子是在规则排列的周期性势场中运动。这 种势场具有晶格的周期性。 对于一维势场: V(x)=V(x+na)
V r V r Rn
4.布罗赫定理 (1)布罗赫定理 在周期性势场V(x)中运动的电子,其能量E(k)和波 函数 k(x)必须满足薛定谔方程,波函数是按晶格周期
调幅的平面波。
(2)布罗赫定理的数学表达式
2 d 2 - +V x ψ k ( x ) E k ψ k ( x ) 2 2m dx
§5.5 布洛赫波
固体电子论—主要研究固体中电子的运动规律。 固体中电子的运动状态对固体的力学、热学、电 磁学、光学等物理性质有着非常重要的影响。因此研
究固体中电子运动规律是固体物理学的一个重要内容。 固体电子论主要包括 1.经典自由电子论(特鲁特-洛伦兹模型); 2.量子力学自由电子理论(索末菲模型); 3.能带理论(布里渊模型)。
k K h x 也是波函数的解。
12
(8)波函数表达式
k x Ahe i k K
u x Ahe
h h iK h x
h
x
e ikx Ahe iK h x e ikxu x
h
(9)u(x)的周期性
u x na Ahe
h
1 2
一个本征值可以和无数 个波矢k、k K 1、k K 2 对应。
3.k的取值范围 为了保证k的取值和本征值一一对应,把k的取值限
制在倒格子的原胞之内。如图红线区域所示。
2 l - k ,k a a Na
N N - l 2 2
波矢k的取值范围称为简约布里渊区(或第一布里渊 区), 其中的波矢称为简约波矢, 共有N个(N是原胞数)。
在K空间, Kh表示倒格点的分布。
2h 2 4 6 Kh , h 0,1,2,。K 1 , K2 , K3 a a a a
K1
4 3 2 a a a
K2
2 a 3 a 4 a
a
O
a
k
2. k x 和 k+K h x 的等同性
单电子近似的理论—把每个电子的运动看成是独立的在 一个等效势场中的运动。
2
一、布洛赫定理
1.不同自由电子模型中的势场分布
(1)特鲁特-洛伦兹模型
忽略晶体的势场。自由电子服从麦克斯韦—玻耳
兹曼分布。 (2)索末菲模型 平均势场,V0 =常数(可选V0=0)。自由电子服从 费米—狄拉克分布。 (3)布里渊模型 周期性势场,势场分布具有晶格的周期性。电子
h
iK h x na
e
iK h na
A e
h h
iK h x
e
i
2h na a
Ahe
h
iK h x
Ahe
h
iK h x
u x
结论:在周期场中运动的粒子的波函数是布洛赫函数。
即调幅的的平面波,调幅函数具有晶体的周期性。
13
二、波矢k的取值范围
1.倒格矢Kh的物理意义
6
(3)周期场近似
周期场近似,所有离子势场和
其它电子的平均场是周期性势场。 (4)单电子近似 将电子气在晶体中运动的多粒子的多体问题近似的 简化为一个电子在周期性势场中运动的问题来处理的方 法称为单电子近似。建立在单电子近似基础上的固体理 论称为能带理论。 (5)近自由电子模型 如果晶体中电子的势能同系统中电子能量的平均值 相比是一个微小量, 可在自由电子模型的基础上作微扰 计算。这种模型称为近自由电子模型。 7
论电子问题时,可以认为离子实是固定在瞬时位置上不 动。电子是在固定不动的离子实产生的势场中运动。晶
格振动以及其它缺陷对电子的影响可以用微扰方法处理。 通过绝热近似, 电子问题。 把多种粒子的多体问题简化为了多
5
(2)平均场近似
由于任何一个电子的运动不仅与它自身的位置有关,
而且还与所有其它电子的位置有关,并且该电子也影响
d u du 2 2 可得: + ik 2 -k u 0 2 dx dx
2
20
(2)特征方程为:
2
r 2ikr -k 0
2 2
r
- ik 2
2ik -4 -k -ik i
2 2 2
r1 -i k ,r2 i -k
V x V x+na =
abc
17
n为任意整数。
2.波函数和薛定谔方程 (1)波函数 根据布罗赫定理可得:
x e ikxux
(2)薛定谔方程 把波函数代入薛定谔方程可得:
2 d 2 V x ψ x Eψ x 2 2m dx
ˆ n x n x T
10
(5)利用波恩-卡门边界条件求出本征值
x+Na x
ˆ N x N x x+Na x T
1, =e 令
N
ika
e
N
ikNa
1
Nka 2l. l 0,1,2,
d 2 2m + 2 E - V 0 2 dx
18
d 2m + 2 E - V 0 2 dx
2
x e ikxux
d 2u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
2 k l. l 0,1,2, Na
ˆ x e ika x T k k
11
(6)本征函数的形式
本征函数 x 如具有 x e ikx的形式,则满足本征方 程。
ˆ x e ika x T k k
ˆ x x+a e ik x a e ika e ikx e ika x T
1
能带理论 是研究固体中电子运动的主要理论基础,能带理论 定性地阐明了晶体中电子运动的普遍性及其特点,说明 了导体、非导体的区别。能带理论提供了分析半导体理 论问题的基础,推动了半导体技术的发展。 随着计算机技术的发展,能带理论的研究从定性
的对普遍性规律的研究发展到对具体材料复杂能带结构
的计算。
能带理论—是建立在单电子近似基础上的固体理论。
(7)波矢的周期性
ˆ T k K h x k K h x+a e i k K h x a e i k K h a e i k K h x
2h Kh h为整数。 a
e ika k K h x k K h x
ika ˆ x e ika x ,T ˆ T k k K h x e k K h x k
14
x 和 k K 有相同的本征值: ika。即 k e k x 、 k K 、 k K 、 都具有相同的本征值。 也即
(3)薛定谔方程的解
2
u x A0e i -k x B0e-i k x A0、B0为任意常数。
21
2.在-b<x<0区域,势能为V0,且E< V0
(1)薛定谔方程
V x
2m 令 = 2 V0 E - 2mV 0 = 2 - 2
2
V0
代入薛定谔方程
ˆ ˆ 2T和H对易性证明
ˆˆ ˆ ˆ ˆ TH x x H x a x a H x T x
ˆ ˆ T和H对易, 所以它们具有共同的本 征函数。
9
ˆ 3T的性质
ˆ Tf x f x a
f x 为任意函数;
15
4.波函数示意图
势能
波函数 实数部分
ux 因子
平面波 实数部分 16
§5.6 克龙尼克(R.Kronig)-潘纳(W.G.Penney)模型 一、克龙尼克-潘纳模型(1931年)
