高一数学二倍角的正
高一数学二倍角公式讲解

在高中数学中同学们感到吃力的一部分是三角函数的学习,在这一部分有大量的公式需要同学们熟练记忆,并且在使用的时候不能够混淆。
为了方便同学们能够清楚掌握这部分内容,在考试中能够取得好成绩,下面小编给大家整理了高中书序中二倍角公式推导讲解。
正弦二倍角公式: sin2α = 2cosαsinα 推导:sin2A=sin(A+A)=sinAcosA+cosAsinA=2sinAcosA 拓展公式:sin2A=2sinAcosA=2tanAcosA^2=2tanA/[1+tanA^2] 1+sin2A=(sinA+cosA)^2余弦二倍角公式: 余弦二倍角公式有三组表示形式,三组形式等价: 1.Cos2a=Cosa^2-Sina^2=[1-tana^2]/[1+tana^2] 2.Cos2a=1-2Sina^2 3.Cos2a=2Cosa^2-1 推导:cos2A=cos(A+A)=cosAcosA-sinAsinA=cosA^2-sinA^2=2cosA^2-1 =1-2sinA^2正切二倍角公式: tan2α=2tanα/[1-tanα^2] 推导:tan2A=tan(A+A)=(tanA+tanA)/(1-tanAtanA)=2tanA/[1-tanA^2]降幂公式: cosA^2=[1+cos2A]/2 sinA^2=[1-cos2A]/2 tanA^2=[1-cos2A]/[1+cos2A] 变式: sin2α=sin^2(α+π/4)-cos^2(α+π/4)=2sin^2(a+π/4)-1=1-2cos^2(α+π/4); cos2α=2sin(α+π/4)cos(α+π/4)以上就是关于高中数学二倍角公式的分享,对于这些公式同学们要掌握他们的推到过程,认真对应三角图形,参考推导过程进行熟练记忆。
最后要强调同学们还是要进行适当的习题训练,加强公式记忆。
高一数学二倍角的三角函数

当 = 时
二倍角公式:
sin 2 2 sin cos
ks5u精品课件
3.若
x 2 sin 1 2 ,则 f x 2 tan x x x sin cos 2 2
2
2
8 f _______ 12
x 1 2 sin 2 2 tan x 2 cos x f ( x ) 2 tan x 2 x x sin x 2 sin cos 2 2
S 2
2
cos 2 cos sin
2
C 2
2 tan tan 2 2 1 tan
k ,且 k ,k Z 2 2 4
ks5u精品课件
T2
二倍角公式
sin 2 2 sin cos
cos2 cos sin 1 2sin 2cos 1
例2.不查表求值: (1)2 cos105 cos15 ;
5 5 2 (2) sin 15 ; 18 9
sin (4)
tan15 (3) 2 ; 1 tan 15
例3.求证:
24
cos
24
cos
12
.
sin 1 sin cos 1 cos sin 1 sin cos 1 cos sin 2
2
ks5u精品课件
灵活运用公式
sin 2 2 sin cos
吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(3)》教案 新人教B版必修4

1吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(3)》教案 新人教B 版必修4(一)复习: 1.二倍角公式sin 22sin cos ααα=22cos 2cos sin ααα=-222cos 112sin αα=-=- 22tan tan 21tan ααα=-【练习1】化简:(1)cos 20cos 40cos 60cos 80 ;(2)sin 10sin 30sin 50sin 70 . ((1)(2)两题答案:116).总结:一般地,11sin(2)cos cos 2cos 4cos 22sin n nn αααααα++⋅⋅⋅=. 2.二倍角公式反映的是将二倍角的三角函数值转化为单角的三角函数值。
在倍角公式中,“倍角”与“半角”是相对的,从而有降幂公式:21cos sin 22αα-=,21cos cos 22αα+=,21cos tan 21cos ααα-=+.(二)新课讲解: 1.半角公式:sin2α=cos2α=tan2α=.说明:(1)只要知道2α角终边所在象限,就可以确定符号;(2)公式的“本质”是用α角的余弦表示2α角的正弦、余弦、正切;(3)还有一个有用的公式:αα-=α+α=αsin cos 1cos 1sin 2tan (下面给出证明)。
2.例题分析:2例1.求证:αα-=α+α=αsin cos 1cos 1sin 2tan.证法一:sin sin 2cos sin 222tan21cos cos cos 2cos222ααααααααα⋅===+⋅ .证法二:221cos (1cos )(1cos )sin tan ()21cos (1cos )(1cos )1cos ααααααααα--+===++++∴sin |sin ||tan|||21cos 1cos ααααα==++. 又由2sin 2sin cos2tancos2222ααααα==知sin α与tan2α同号,且1cos 0α+≥,∴sin tan21cos ααα=+, 同理1cos tan2sin ααα-=.【练习2】已知3sin 25θ=,且022πθ<<,求22cossin 12)4θθπθ--+的值。
二倍角的正弦、余弦、正切公式

归纳小结
(1)二倍角公式是和角公式的特例,体现了 二倍角公式是和角公式的特例, 二倍角公式是和角公式的特例 将一般化归为特殊的基本数学思想方法。 将一般化归为特殊的基本数学思想方法。 (2)二倍角公式与和角、差角公式一样,反 二倍角公式与和角、 二倍角公式与和角 差角公式一样, 映的都是如何用单角α的三角函数值表示 映的都是如何用单角 的三角函数值表示 复角( 的三角函数值, 复角(和、差、倍)的三角函数值,结合 前面学习到的同角三角函数关系式和诱导 公式可以解决三角函数中有关的求值、 公式可以解决三角函数中有关的求值、化 简和证明问题。 简和证明问题。
化简 sin 50 (1 + 3 tan10 )
o o
cos10o + 3 sin 10o o 解: 原式 = sin 50 ⋅ o cos10 o o 2 sin 40 = sin 50 ⋅ o cos10 o o 2 sin 40 = cos 40 ⋅ o cos10 o sin 80 = =1 o cos10
[例2]若270°<α<360°, 化简:
1 1 + 2 2
求值
1 1 + cos 2α 2 2
(1)cos80°cos40°cos20° (2)sin10°sin30°sin50°sin70°
例3
1+sin2 −cos2 θ θ 求 : 证 = tanθ 1+sin2 +cos2 θ θ
2
1 + 2 sin θ cos θ − (1 − 2 sin θ ) 证明: 证明:左边 = 2 1 + 2 sin θ cos θ + ( 2 cos θ − 1)
同样对于正切也有这样的结论
5.5.1第三课时二倍角的正弦、余弦、正切公式课件高一上学期数学人教A版(2019)必修第一册

2
+
1-cos (2 -30°)
2
+cos θsin θ
1
=1+2(cos 2θcos 30°-sin 2θsin 30°-cos 2θcos 30°-sin 2θsin 30°)
1
1
+2sin 2θ=1-sin 2θsin 30°+2sin 2θ=1.
(2)证明 左边=
(1-cos2 )+sin2
A.2sin 15°cos 15°
B.cos215°-sin215°
C.2sin215°
D.sin215°+cos215°
2.若 sin
α
3
= ,则 cos α等于
2 3
2
1
A.-
B.-
3
3
π
π
3.sin4 -cos4 等于
12
12
1
A.-
2
B.-
3
2
1
C.
3
1
C.
2
2
D.
3
D.
3
2
跟踪训练
4.cos275°+cos215°+cos 75°cos 15°的值等于
二倍关系.
(3)注意几种公式的灵活应用,如:
①sin
π
π
2x=cos2-2x=cos24-x
=2cos
②cos
π
π
2x=sin2-2x=sin24-x
π
π
=2sin4-xcos4-x.
5.5.1二倍角的正弦、余弦、正切公式2024-2025学年高一上学期数学人教A版(2019)必修一

2
2
即 cos 2α=cos α-sin α;tan(α+α)=
,即 tan 2α=
.
-
-
2.根据同角三角函数的基本关系sin2α+cos2α=1,能否只用sin α
或cos α表示cos 2α?
提示:cos 2α=cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1;
=
+
+
-
=sin +cos +sin -cos =2sin .
以上解答过程中都有哪些错误?出错的原因是什么?你如何改
正?你如何防范?
提示:在去根号时,对 sin±cos的符号未加以讨论,导致化简
错误.
正解:原式= + + -
+
=
+
=
.
D.
)
探究三 利用倍角公式化简、证明
【例 3】 化简:
-
-
+
.
分析:首先切化弦,然后利用二倍角公式统一角,最后化简得结
果.
解:方法一:
原式=
-
-
·
=-
.
2.将本例变为“已知 sin
又 sin
人教版高一数学必修四第三章二倍角的正弦、余弦、正切公式
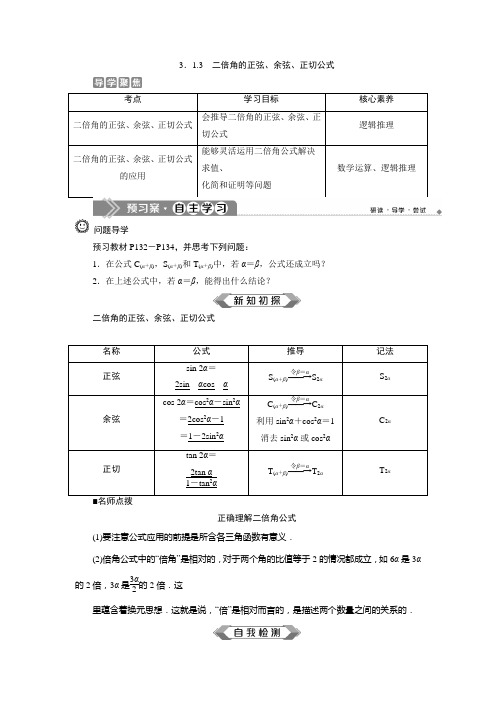
3.1.3二倍角的正弦、余弦、正切公式考点学习目标核心素养二倍角的正弦、余弦、正切公式会推导二倍角的正弦、余弦、正切公式逻辑推理二倍角的正弦、余弦、正切公式的应用能够灵活运用二倍角公式解决求值、化简和证明等问题数学运算、逻辑推理问题导学预习教材P132-P134,并思考下列问题:1.在公式C(α+β),S(α+β)和T(α+β)中,若α=β,公式还成立吗?2.在上述公式中,若α=β,能得出什么结论?二倍角的正弦、余弦、正切公式名称公式推导记法正弦sin 2α=2sin__αcos__αS(α+β)――→令β=αS2αS2α余弦cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2αC(α+β)――→令β=αC2α利用sin2α+cos2α=1消去sin2α或cos2αC2α正切tan 2α=2tan α1-tan2αT(α+β)――→令β=αT2αT2α正确理解二倍角公式(1)要注意公式应用的前提是所含各三角函数有意义.(2)倍角公式中的“倍角”是相对的,对于两个角的比值等于2的情况都成立,如6α是3α的2倍,3α是3α2的2倍.这里蕴含着换元思想.这就是说,“倍”是相对而言的,是描述两个数量之间的关系的.判断(正确的打“√”,错误的打“×”) (1)10α是5α的倍角,5α是5α2的倍角.( ) (2)二倍角的正弦、余弦、正切公式的适用范围是任意角.( ) (3)存在角α,使得sin 2α=2sin α成立.( ) (4)对于任意角α,总有tan 2α=2tan α1-tan 2α.( )答案:(1)√ (2)× (3)√ (4)×已知sin α=35,cos α=45,则sin 2α等于( )A.75 B.125 C.1225 D.2425答案:D计算1-2sin 222.5°的结果等于( ) A.12 B.22 C.33D.32 答案:B已知tan α=43,则tan 2α=________.答案:-247给角求值求下列各式的值. (1)sin π8cos π8;(2)cos 2π6-sin 2π6;(3)2tan 150°1-tan 2150°; (4)cos π5cos 2π5.【解】 (1)sin π8cos π8=12×2sin π8cos π8=12×sin π4=12×22=24.(2)cos2π6-sin2π6=cos⎝⎛⎭⎫2×π6=cosπ3=12.(3)原式=tan(2×150°)=tan 300°=tan(360°-60°)=-tan 60°=- 3.(4)原式=2sinπ5cosπ5cos2π52sinπ5=sin2π5cos2π52sinπ5=sin4π54sinπ5=sinπ54sinπ5=14.给角求值问题的两类解法(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式进行转化,一般可以化为特殊角.(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.1.cos4π12-sin4π12等于()A.-12B.-32C.12 D.32解析:选D.原式=⎝⎛⎭⎫cos2π12-sin2π12⎝⎛⎭⎫cos2π12+sin2π12=cos π6=32.2.求下列各式的值.(1)tan 30°1-tan2 30°;(2)1sin 10°-3cos 10°.解:(1)tan 30°1-tan230°=12×2tan 30°1-tan230°=12tan 60°=32.(2)原式=cos 10°-3sin 10°sin 10°cos 10°=2⎝⎛⎭⎫12cos 10°-32sin 10°sin 10°cos 10°=4(sin 30°cos 10°-cos 30°sin 10°)2sin 10°cos 10°=4sin (30°-10°)sin (2×10°)=4sin 20°sin 20°=4.给值求值已知cos ⎝⎛⎭⎫α+π4=35,π2≤α<3π2,求cos(2α+π4)的值. 【解】 因为π2≤α<3π2,所以3π4≤α+π4<7π4.因为cos ⎝⎛⎭⎫α+π4>0,所以3π2<α+π4<7π4. 所以sin ⎝⎛⎭⎫α+π4=-1-cos 2⎝⎛⎭⎫α+π4 =-1-⎝⎛⎭⎫352=-45. 所以cos 2α=sin ⎝⎛⎭⎫2α+π2 =2sin ⎝⎛⎭⎫α+π4cos ⎝⎛⎭⎫α+π4 =2×⎝⎛⎭⎫-45×35=-2425, sin 2α=-cos ⎝⎛⎭⎫2α+π2=1-2cos 2⎝⎛⎭⎫α+π4 =1-2×⎝⎛⎭⎫352=725.所以cos ⎝⎛⎭⎫2α+π4=22cos 2α-22sin 2α =22×⎝⎛⎭⎫-2425-725=-31250.三角函数求值问题的一般思路(1)一是对题设条件变形,将题设条件中的角、函数名向结论中的角、函数名靠拢;另一种是对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.(2)注意几种公式的灵活应用,如: ①sin 2x =cos ⎝⎛⎭⎫π2-2x =cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4-x =2cos 2⎝⎛⎭⎫π4-x -1=1-2sin 2⎝⎛⎭⎫π4-x ; ②cos 2x =sin ⎝⎛⎭⎫π2-2x =sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4-x =2sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x .1.已知x ∈⎝⎛⎭⎫-π2,0,cos x =45,则tan 2x =( ) A.724 B .-724 C.247D .-247解析:选D.由cos x =45,x ∈⎝⎛⎭⎫-π2,0, 得sin x =-35,所以tan x =-34,所以tan 2x =2tan x1-tan 2x =2×⎝⎛⎭⎫-341-⎝⎛⎭⎫-342=-247,故选D.2.若α∈⎝⎛⎭⎫π2,π,且3cos 2α=sin ⎝⎛⎭⎫π4-α,则sin 2α的值为( )A.118 B .-118 C.1718D .-1718解析:选 D.cos 2α=sin ⎝⎛⎭⎫π2-2α=sin 2⎝⎛⎭⎫π4-α=2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α,代入原式,得6sin ⎝⎛⎭⎫π4-α·cos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4-α.因为α∈⎝⎛⎭⎫π2,π,所以cos ⎝⎛⎭⎫π4-α=16,所以sin 2α=cos ⎝⎛⎭⎫π2-2α=2cos 2⎝⎛⎭⎫π4-α-1=-1718.化简与证明(1)化简2cos 2α-12tan ⎝⎛⎭⎫π4-αsin 2⎝⎛⎭⎫π4+α;(2)证明tan ⎝⎛⎭⎫π4+α-tan ⎝⎛⎭⎫π4-α=2tan 2α. 【解】 (1)原式=cos 2α2tan ⎝⎛⎭⎫π4-αcos 2⎝⎛⎭⎫π2-π4-α=cos 2α2tan ⎝⎛⎭⎫π4-αcos 2⎝⎛⎭⎫π4-α=cos 2α2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α =cos 2αsin ⎝⎛⎭⎫2×π4-2α =cos 2αcos 2α=1. (2)证明:法一:左边=sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α-sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4-α-sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4+α-π4+αcos ⎝⎛⎭⎫π4+αsin ⎝⎛⎭⎫π4+α=sin 2α12sin ⎝⎛⎭⎫π2+2α=2sin 2αcos 2α=2tan 2α=右边.所以等式成立.法二:左边=1+tan α1-tan α-1-tan α1+tan α=4tan α1-tan 2α=2tan 2α=右边.故原式成立.三角函数式的化简与证明(1)化简的方法①弦切互化,异名化同名,异角化同角;②降幂或升幂;③一个重要结论:(sin θ±cos θ)2=1±sin 2θ.(2)证明三角恒等式的方法①从复杂的一边入手,证明一边等于另一边;②比较法,左边-右边=0,左边右边=1;③分析法,从要证明的等式出发,一步步寻找等式成立的条件.1.若α为第三象限角,则1+cos 2αcos α-1-cos 2αsin α=________.解析:因为α为第三象限角,所以cos α<0,sin α<0, 所以1+cos 2αcos α-1-cos 2αsin α=2cos 2αcos α-2sin 2αsin α=-2cos αcos α--2sin αsin α=0.答案:02.求证:4sin αcos α1+cos 2α·cos 2αcos 2α-sin 2α=tan 2α.证明:左边=2sin 2α2cos 2α·cos 2αcos 2α=tan 2α=右边.1.已知sin α=3cos α,那么tan 2α的值为( ) A .2 B .-2 C.34D .-34解析:选D.因为sin α=3cos α,所以tan α=3, 所以tan 2α=2tan α1-tan 2α=2×31-32=-34.2.已知sin θ2+cos θ2=233,那么sin θ=________,cos 2θ=________.解析:因为sin θ2+cos θ2=233,所以⎝⎛⎭⎫sin θ2+cos θ22=43, 即1+2sin θ2cos θ2=43,所以sin θ=13,所以cos 2θ=1-2sin 2θ=1-2×⎝⎛⎭⎫132=79. 答案:13 793.已知α∈⎝⎛⎭⎫π2,π,sin α=55. (1)求sin 2α,cos 2α的值; (2)求cos ⎝⎛⎭⎫5π6-2α的值. 解:(1)因为α∈⎝⎛⎭⎫π2,π,sin α=55, 所以cos α=-1-sin 2α=-255.sin 2α=2sin αcos α=2×55×⎝⎛⎭⎫-255=-45, cos 2α=1-2sin 2α=1-2×⎝⎛⎭⎫552=35. (2)由(1)知cos ⎝⎛⎭⎫5π6-2α=cos 5π6cos 2α+sin 5π6sin 2α =⎝⎛⎭⎫-32×35+12×⎝⎛⎭⎫-45 =-4+3310.[A 基础达标]1.已知sin ⎝⎛⎭⎫π4-x =35,则cos ⎝⎛⎭⎫π2-2x 的值为( )A.1925 B.1625 C.1425D.725解析:选D.因为sin ⎝ ⎛⎭⎪⎫π4-x =35,所以cos ⎝ ⎛⎭⎪⎫π2-2x =cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-x=1-2sin 2⎝ ⎛⎭⎪⎫π4-x =725.2.已知sin α=55,则cos 4α-sin 4α的值为( ) A .-35B .-15C.15D.35解析:选D.cos 4α-sin 4α=(cos 2α+sin 2α)(cos 2α-sin 2α)=cos 2α=1-2sin 2α=1-25=35.3.设-3π<α<-5π2,化简1-cos (α-π)2的结果是( )A .sin α2B .cos α2C .-cos α2D .-sin α2解析:选C.因为-3π<α<-5π2,-3π2<α2<-5π4,所以1-cos (α-π)2=1+cos α2=⎪⎪⎪⎪⎪⎪cos α2=-cos α2.4.已知cos ⎝⎛⎭⎫α-π4=-13,则sin(-3π+2α)=( )A.79 B .-79C.35D .-35解析:选A.易得cos ⎝ ⎛⎭⎪⎫2α-π2=2cos 2⎝ ⎛⎭⎪⎫α-π4-1=2×⎝⎛⎭⎫-132-1=-79.又cos ⎝⎛⎭⎪⎫2α-π2=cos ⎝ ⎛⎭⎪⎫π2-2α=sin 2α,所以sin(-3π+2α)=sin(π+2α)=-sin 2α=-⎝⎛⎭⎫-79=79.故选A. 5.化简tan 14°1-tan 214°·cos 28°的结果为( )A.sin 28°2B .sin 28°C .2sin 28°D .sin 14°cos 28°解析:选A.tan 14°1-tan 214°·cos 28°=12×2tan 14°1-tan 214°·cos 28°=12tan 28°·cos 28°=sin 28°2,故选A.6.已知sin α-2cos α=0,则tan 2α=________. 解析:由sin α-2cos α=0,得tan α=sin αcos α=2,tan 2α=2tan α1-tan 2α=2×21-22=-43. 答案:-437.已知tan α=-13,则sin 2α-cos 2α1+cos 2α=________.解析:sin 2α-cos 2α1+cos 2α=2sin αcos α-cos 2α1+2cos 2α-1=2sin αcos α-cos 2α2cos 2α=tan α-12=-56.答案:-568.1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=________.解析:1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=(cos 20°-sin 20°)2cos 20°-sin 20°=cos 20°-sin 20°cos 20°-sin 20°=1.答案:19.已知sin 2α=513,π4<α<π2,求sin 4α,cos 4α的值.解:由π4<α<π2,得π2<2α<π. 因为sin 2α=513,所以cos 2α=-1-sin 22α=-1-⎝⎛⎭⎫5132=-1213. 于是sin 4α=2sin 2αcos 2α=2×513×⎝⎛⎭⎫-1213=-120169; cos 4α=1-2sin 22α=1-2×⎝⎛⎭⎫5132=119169. 10.已知π2<α<π,sin α=45. (1)求tan 2α的值;(2)求cos ⎝⎛⎭⎫2α-π4的值. 解:(1)由题意得cos α=-35, 所以tan α=-43, 所以tan 2α=2tan α1-tan 2α=-831-169=247. (2)因为sin α=45,所以cos 2α=1-2sin 2α=1-2×⎝⎛⎭⎫452=-725, sin 2α=2sin α·cos α=2×45×⎝⎛⎭⎫-35=-2425. 所以cos ⎝⎛⎭⎪⎫2α-π4=cos 2α·cos π4+sin 2α·sin π4=⎝⎛⎭⎫-725×22+⎝⎛⎭⎫-2425×22=-31250. [B 能力提升]11.已知tan x =2,则tan ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4等于( ) A.43B .-43 C.34 D .-34解析:选C.tan ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π4 =tan ⎝ ⎛⎭⎪⎫2x -π2=sin ⎝ ⎛⎭⎪⎫2x -π2cos ⎝ ⎛⎭⎪⎫2x -π2=-cos 2x sin 2x =-1tan 2x=-1-tan 2x 2tan x =4-12×2=34. 12.已知θ∈⎝⎛⎭⎫π2,π,1sin θ+1cos θ=22,则sin ⎝⎛⎭⎫2θ+π3=________. 解析:1sin θ+1cos θ=22⇒sin θ+cos θsin θcos θ=22 ⇒sin θ+cos θ=22sin θcos θ⇒1+sin 2θ=2sin 22θ,因为θ∈⎝ ⎛⎭⎪⎫π2,π,所以2θ∈(π,2π), 所以sin 2θ=-12,所以sin θ+cos θ<0, 所以θ∈⎝ ⎛⎭⎪⎫3π4,π,所以2θ∈⎝ ⎛⎭⎪⎫3π2,2π, 所以cos 2θ=32,所以sin ⎝⎛⎭⎪⎫2θ+π3=sin 2θ·cos π3+sin π3cos 2θ=12. 答案:1213.已知sin ⎝⎛⎭⎫π4-x =513,0<x <π4,求cos 2x cos ⎝⎛⎭⎫π4+x 的值. 解:因为0<x <π4,所以0<π4-x <π4. 又因为sin ⎝ ⎛⎭⎪⎫π4-x =513, 所以cos ⎝ ⎛⎭⎪⎫π4-x =1213. 因为cos 2x =sin ⎝ ⎛⎭⎪⎫π2-2x =2sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x =2sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x=2cos ⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x , 所以cos 2x cos ⎝ ⎛⎭⎪⎫π4+x =2cos ⎝ ⎛⎭⎪⎫π4-x =2413. 14.(选做题)已知sin x 2-2cos x 2=0. (1)求tan x 的值;(2)求cos 2xcos ⎝⎛⎭⎫5π4+x sin (π+x )的值.解:(1)由sin x 2-2cos x 2=0, 知cos x 2≠0,所以tan x 2=2, 所以tan x =2tan x 21-tan 2 x 2=2×21-22=-43. (2)由(1)知tan x =-43, 所以cos 2x cos ⎝ ⎛⎭⎪⎫5π4+x sin (π+x ) =cos 2x-cos ⎝ ⎛⎭⎪⎫π4+x (-sin x ) =cos 2x -sin 2x ⎝⎛⎭⎫22cos x -22sin x sin x =(cos x -sin x )(cos x +sin x )22(cos x -sin x )sin x =2×cos x +sin x sin x=2×1+tan x tan x =24.。
第3课时 二倍角的正弦、余弦、正切公式 课件(共11张PPT) 高一数学人教A版必修第一册

sin 4α
120
tan 4α =
=−
.
cos 4α
119
注意:“倍”是两个数量间一种相对的关系,如 2α 是 α 的二倍,4α 又是 2α
的二倍,
2
是
4
的二倍;应准确理解“倍”的含义,灵活运用倍角公式.
学习目标
新课讲授
课堂总结
练一练
3
5
1. 已知 sin (α – π) = ,求 cos 2α 的值.
1 – tan 2A· tan 2B 117
思考:上述题目还有没有其他的解答方法,若有,请说出其他解法,若没
有,请说明理由.
将 tan (2A+2B) 视为 tan 2(A+B),先求出 tan (A+B)的值,再利用倍角公式即可.
学习目标
新课讲授
课堂总结
练一练
2. 已知 tan 2α =
1
,求
3
5.5.1.3 二倍角的正弦、余弦、正切公式
学习目标
新课讲授
课堂总结
1. 掌握二倍角的正弦、余弦、正切公式及其推导过程;(重点)
2. 能灵活运用二倍角公式解决有关的化简、求值等问题.(难点)
学习目标
新课讲授
课堂总结
知识点 1 :二倍角的正弦、余弦、正切公式
忆一忆:按照相应规律,说出所有的和(差)角公式!
sin (α + β) = sinα·cosβ + cosα·sinβ
sin (α − β) = sinα·cosβ − cosα·sinβ
cos (α + β) = cosα·cosβ − sinα·sinβ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
快三交流群
