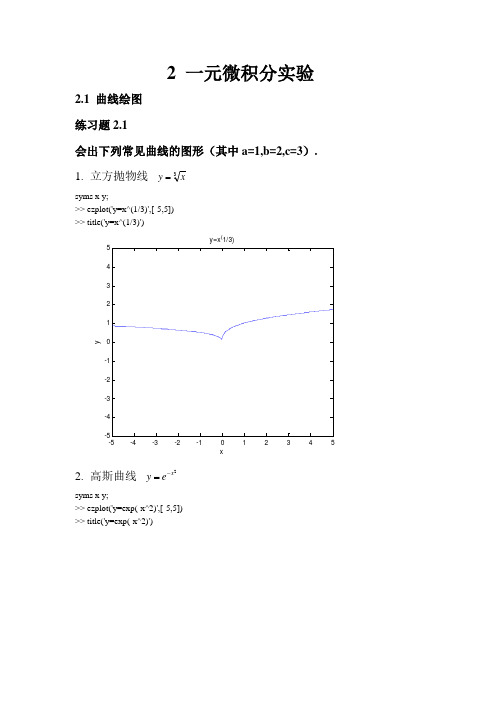
数学实验1

数学实验实验报告Mathematical Experiment Report
学生所在学院：理学院
学生所在班级：11级数理统计（1）班学生姓名：姜景耀
指导教师：李建东
教务处
2013年 9月
1.实验内容
① 函数图形的描绘；② 函数的多项式逼近——Taylor 级数； ③ Fourier 级数； ④ 无穷乘积；⑤ 调和级数
2.实验目的
学习使用Mathematica 的一些基本功能来验证或观察微积分学的几个结论。

3.实验要求
在熟悉相关命令的使用方法后，解决下列问题：(函数自选) ① 绘制函数的图形，观察分析函数、导函数之间的联系，寻求函数的零点。

x x x f 43
1
)(3+-= 4)(2+-='x x f
Plot[{(-1/3)x^3+4x,-x^2+4},{x,-4,4}]
1，当0)(>'x f 时，图像上升。

当0)(<'x f 时，图像下降。

当0)(='x f 时有极值。

2，当)(x f '上升时，图像凹。

当)(x f '下降时，图像凸。

当0)(='x f 时，)
(x f 图像出现拐点。

3，观察得出方程0)(=x f 的根，近似为5.31-=x ，02=x ，5.33=x 精确值：
一、 FindRoot[{4x-x 3/3},{x,-2,-4}] {x -3.4641}
二、 FindRoot[{4x-x 3/3},{x,-2,2}]
{x 0.}
三、 FindRoot[{4x-x 3/3},{x,4,2}] {x 3.4641}
② 计算函数的Taylor 级数，并观察函数对应级数的收敛情况，试给出收敛和不收敛的例子(图形)。

x x f sin )(=
Taylor 级数：∑∞
=++-0
1
2)!12()1(k k k
k x
Series[Sin[x],{x,0,9}] x-x 3/6+x 5/120-x 7/5040+x 9/362880+O[x]10
Plot[{x-x 3/6+x 5/120,x-x 3/6+x 5/120-x 7/5040+x 9/362880,x-x 3/6+x 5/120-x 7/5040+x 9/362880-x 11/39916800,Sin[x]},{x,-pi,pi}]
有图可知，当k 逐渐增大时，级数∑∞
=++-01
2)!12()1(k k k
k x 的图像越接近于x sin ，
我们猜测当∞→k 时，∑∞
=++-0
1
2)!12()1(k k k
k x 收敛于x sin 。

11
)(+=
x x f ，经计算可知其泰勒级数为n n n x ∑∞
=-0
)1(，有图形可知其泰勒级数在][∞,1上不收敛于其本身，在[-1,1]收敛其本身。

③ 计算函数的Fourier 级数，并观察其收敛性。

⎩⎨⎧=≤≤--≤≤0,4
0,4)(x x x f ππ
ππ
Fourier 级数为：∑
∞
=--=1
12)
2s in (),(n n x nx n x f ，下面俩图分别为10=n 和
1000=n 时，∑
∞
=--=1
12)
2sin(),(n n x
nx n x f 的图像。

定义函数： f[x_,n_]:=Sum[Sin[2k*x-x]/(2k-1),{k,1,n}];
Plot[f[x,10],{x,-6,4}] Plot[f[x,1000],{x,-6,4}]
④观察无穷乘积
222
22222
111
2
x x x
x
n
πππ
⎛⎫⎛⎫⎛⎫
⋅-⋅--
⎪ ⎪ ⎪
⎝⎭⎝⎭⎝⎭
的敛散性，并与函数
sin
y x
=的图形作比较，观察、分析二者之间的联系。

定义函数： g[x_,n_]:=x*Product[1-(x^2/(k* )^2),{k,1,n}]; Plot[{g[x,5],g[x,10],g[x,50]},{x,-15,15}]
Plot[{Sin[x],g[x,5],g[x,50],g[x,500]},{x,-15,15}]
第一图可以看出无穷乘积收敛于某函数，第二图可以看出其收敛于sin[x];。