《数学实验》王向东高等教育出版社实验一习题详解

合集下载

数学实验(第二版)课后习题答案

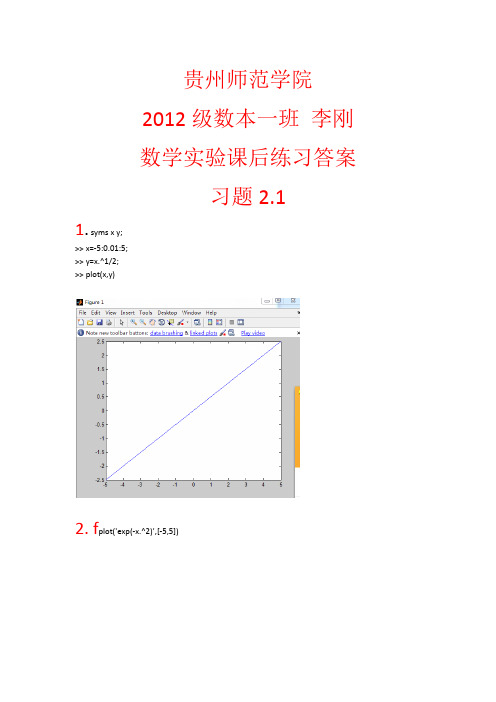
贵州师范学院2012级数本一班李刚数学实验课后练习答案习题2.11. syms x y;>> x=-5:0.01:5;>> y=x.^1/2;>> plot(x,y)2. f plot('exp(-x.^2)',[-5,5])3. ezplot('x.^3+y.^3-3*x*y',[-5,5])4 . ezplot('y.^2-x.^3/(1-x)',[-5,5])5.t=0:0.1:2*pi;x=t-sin(t);y=2*(1-cos(t));plot(x,y)6. t=0:0.1:2*pi; x=cos(t).^3; >> y=sin(t).^3;>> plot(t,y)>>7: t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z)8: x =0:0.1:2*pi; r=x; polar(x,r)9: x =0:0.1:2*pi; r=exp(x); polar(x,r)10: x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)11: x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)12: x =0:0.1:2*pi; r=1+cos(x); polar(x,r)练习2.2 1：(1)(2)：syms n; limit('sqrt(n+2)-2*(sqrt(n+1))+sqrt(n)',n,inf)Ans= 0 (3):: (4):(5):(6):2:3:fplot('x.^2*sin(x.^2-x-2)',[-2,2])练习2.3 1：（2）：2：练习2.4 1：（1）（2）：（3）（4）：2：（1）：syms x;int(x^(-x),x,0,1)ans =int(x^(-x),x = 0 .. 1)vpa(ans,10)ans =1.291285997（2）：syms x；int(exp(2*x)*cos(x)^3,x,0,2*pi)ans =-22/65+22/65*exp(4*pi)（3）：syms x; int(exp(x^2/2)/sqrt(2*pi),x,0,1)ans =-1125899906842624/5644425081792261*i*erf(1/2*i*2^(1/2))*pi^(1/2)*2^(1/2) >> vpa(ans,10)ans =.4767191345（4）：syms x;int(x*log(x^4)*asin(1/x^2),x,1,3)ans =int(x*log(x^4)*asin(1/x^2),x = 1 .. 3)>> vpa(ans,10)ans =2.459772128（5）：syms x ;int(exp(x^2/2)/sqrt(2*pi),x,-inf,inf)ans =Inf（6）：syms x ;int(sin(x)/x,x,0,inf)ans =1/2*pi（7）：syms x ;int(tan(x)/sqrt(x),x,0,1)Warning: Explicit integral could not be found. > In sym.int at 58ans =int(tan(x)/x^(1/2),x = 0 .. 1)>> vpa(ans,10)ans =.7968288892（8）：syms x ;int(exp(-x^2/2)/(1+x^4),x,-inf,inf)ans =1/4*pi^(3/2)*2^(1/2)*(AngerJ(1/2,1/2)-2/pi^(1/2)*sin(1/2)+2/pi^(1/2)*cos(1/2)-WeberE(1/2,1/2 ))>> vpa(ans,10)ans =1.696392536（9）：syms x ;int(sin(x)/sqrt(1-x^2),x,0,1)ans =1/2*pi*StruveH(0,1)>> vpa(ans,10)ans =.8932437410练习2.5（1）：syms n;symsum(1/n^2^n,n,1,inf)ans =sum(1/((n^2)^n),n = 1 .. Inf)（2）：s yms n ;symsum(sin(1/n),n,1,inf)ans =sum(sin(1/n),n = 1 .. Inf)（3）：syms n ;symsum(log(n)/n^3,n,1,inf) ans =-zeta(1,3)（4）：syms n ;symsum(1/(log(n))^n,n,3,inf) ans =sum(1/(log(n)^n),n = 3 .. Inf)（5）：syms n;symsum(1/(n*log(n)),n,2,inf) ans =sum(1/n/log(n),n = 2 .. Inf)（6）：yms n;symsum((-1)^n*n/(n^2+1),n,1,inf)ans =-1/4*Psi(1-1/2*i)+1/4*Psi(1/2-1/2*i)-1/4*Psi(1+1/2*i)+1/4*Psi(1/2+1/2*i)第三章练习3.11：（1）：a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=10*sin(sqrt(x.^2+y.^2))./(sqrt(1+x.^2+y.^2)); meshc(x,y,z)（2）：a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b);z=4*x.^2/9+y.^2;meshc(x,y,z)（3）：（4）：a=-30:1:30;b=-30:1:30;[x,y]=meshgrid(a,b); z=x.^2/3-y.^2/3; meshc(x,y,z)（5）：a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=x*y;>> meshc(x,y,z)（6）：（7）：a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b); >> z=sqrt(x.^2+y.^2); >> meshc(x,y,z)（8）：（9）：a=-30:1:30;>> b=-30:1:30;>> [x,y]=meshgrid(a,b);>> z=atan(x./y);>> meshc(x,y,z)练习3.21;a=-1:0.1:1;>> b=0:0.1:2;>> [x,y]=meshgrid(a,b);>> z=x.*exp(-x.^2-y.^2);>> [px,py]=gradient(z,0.1,0.1);>> contour(a,b,z)>> hold on>> quiver(a,b,px,py)2:a=-2:0.1:1;>> b=-7:0.1:1;>> [x,y]=meshgrid(a,b);>> z=y.^3/9+3*x.^2.*y+9*x.^2+y.^2+x.*y+9; >> plot3(x,y,z)>> grid on3:[x,y]=meshgrid(-2*pi:0.2:2*pi); z=x.^2+2*y.^2;plot3(x,y,z)hold onezplot('x^2+y^2-1',[-2*pi,2*pi]) ; grid on4:t=0:0.03:2*pi;>> s=[0:0.03:2*pi]';>> x=(0*s+1)*cos(t);y=(0*s+1)*sin(t);z=s*(0*t+1); >> mesh(x,y,z)>> hold on>> [x,y]=meshgrid(-1:0.1:1);>> z=1-x+y;>> mesh(x,y,z)5:syms x y z dx dyz=75-x^2-y^2+x*y;zx=diff(z,x),zy=diff(z,y)zx =-2*x+yzy =-2*y+x练习3.31：ezplot('x^2+y^2-2*x',[-2,2]);>> grid onsyms x y ;s=int(int(x+y+1,y,-sqrt(1-(x-1)^2),sqrt(1-(x-1)^2)),x,0,2)s =2*pi2：syms r t ;>> s=int(int(sqrt(1+r^2*sin(t)),r,0,1),t,0,2*pi)s =int(1/2*((1+sin(t))^(1/2)*sin(t)^(1/2)+log(sin(t)^(1/2)+(1+sin(t))^(1/2)))/sin(t)^(1/2),t = 0 .. 2*pi) 3：syms x y z ;>> s=int(int(int(1/(1+x+y+z)^3,z,0,1-x-y),y,0,1-x),x,0,1)s =-5/16+1/2*log(2)4：s=vpa(int(int(x*exp(-x^2-y^2),y,0,2),x,-1,10))s =0.16224980455070416645061789474030练习3.41：（1）：y=dsolve('Dy=x+y','y(0)=1','x')得：y =-1-x+2*exp(x)（2）：y=dsolve('Dy=2*x+y^2','y(0)=0')y =tan(t*x^(1/2)*2^(1/2))*x^(1/2)*2^(1/2)练习4.11：（1）：p=[5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -6 8 0 0 0 -5 0 0]; >> x=roots(p)x =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927（2）: p=[8 36 54 23];x=roots(p)x =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.70632:p1=[1 0 -3 -2 -1];p2=[1 -2 5];[q2,r2]=deconv(p1,p2)q2 =1 2 -4r2 =0 0 0 -20 19 3:syms x;f=x^4+3*x^3-x^2-4*x-3;g=3*x^3+10*x^2+2*x-3;p1=factor(f),p2=factor(g)p1 =(x+3)*(x^3-x-1)p2 =(x+3)*(3*x^2+x-1)4:syms x ;f=x^12-1;p=factor(f)p =(-1+x)*(1+x^2+x)*(1+x)*(1-x+x^2)*(1+x^2)*(x^4-x^2+1)5: (1):p=[1 0 1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.0000 - 0.3536i-0.0000 + 0.3536i0.0000 - 0.3536i0.0000 + 0.3536ib =0.7071 + 0.7071i0.7071 - 0.7071i-0.7071 + 0.7071i-0.7071 - 0.7071ir =[](2):p=[1];q=[1 0 0 0 1];[a,b,r]=residue(p,q)a =-0.1768 - 0.1768i -0.1768 + 0.1768i0.1768 - 0.1768i0.1768 + 0.1768ib =0.7071 + 0.7071i0.7071 - 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071ir =[](3):p=[1 0 1];q=[1 1 -1 -1];[a,b,r]=residue(p,q)a =0.5000-1.00000.5000b =-1.0000-1.00001.0000r =[] (4): p=[1 1 0 0 0 -8];[a,b,r]=residue(p,q)a =-4-38b =-11r =1 1 1练习 4.21：（1）：D=[2 1 3 1;3 -1 2 1;1 2 3 2;5 0 6 2];det(D)ans =6（2）：syms a b c dD=[a 1 0 0 ;-1 b 1 0;0 -1 c 1;0 0 -1 d];det(D)ans =a*b*c*d+a*b+a*d+c*d+12：（1）：D=[1 1 1 1; a b c d;a^2 b^2 c^2 d^2;a^3 b^3 c^3 d^3];det(D)ans =b*c^2*d^3-b*d^2*c^3-b^2*c*d^3+b^2*d*c^3+b^3*c*d^2-b^3*d*c^2-a*c^2*d^3+a*d^2*c^3+a *b^2*d^3-a*b^2*c^3-a*b^3*d^2+a*b^3*c^2+a^2*c*d^3-a^2*d*c^3-a^2*b*d^3+a^2*b*c^3+a^ 2*b^3*d-a^2*b^3*c-a^3*c*d^2+a^3*d*c^2+a^3*b*d^2-a^3*b*c^2-a^3*b^2*d+a^3*b^2*c（2）: s yms a b x y zD=[a*x+b*y a*y+b*z a*z+b*x; a*y+b*z a*z+b*x a*x+b*y;a*z+b*x a*x+b*y a*y+b*z];det(D)ans =3*a^3*x*z*y+3*b^3*y*x*z-a^3*x^3-a^3*y^3-b^3*z^3-a^3*z^3-b^3*x^3-b^3*y^33: (1): D=[1 1 1 1;1 2 -1 4;2 -3 -1 -5;3 1 2 11];D1=[5 1 1 1;-2 2 -1 4;-2 -3 -1 -5;0 1 2 11];D2=[1 5 1 1;1 -2 -1 4;2 -2 -1 -5;3 0 2 11];D3=[1 1 5 1;1 2 -2 4;2 -3 -2 -5;3 1 0 11];D4=[1 1 1 5;1 2 -1 -2;2 -3 -1 -2;3 1 2 0];x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x1,x2,x3,x4x1 =1x2 =2x3 =3x4 =-1(2):D=[5 6 0 0 0;1 5 6 0 0;0 1 5 6 0;0 0 1 5 6;0 0 0 1 5]; D1=[1 6 0 0 0;0 5 6 0 0;0 1 5 6 0;0 0 1 5 6;1 0 0 1 5]; D2=[5 1 0 0 0;1 0 6 0 0;0 0 5 6 0;0 0 1 5 6;0 1 0 1 5]; D3=[5 6 1 0 0;1 5 0 0 0;0 1 0 6 0;0 0 0 5 6;0 0 1 1 5]; D4=[5 6 0 1 0;1 5 6 0 0;0 1 5 0 0;0 0 1 0 6;0 0 0 1 5]; D5=[5 6 0 0 1;1 5 6 0 0;0 1 5 6 0;0 0 1 5 0;0 0 0 1 1]; x1=det(D1)/det(D);x2=det(D2)/det(D);x3=det(D3)/det(D);x4=det(D4)/det(D);x5=det(D5)/det(D);x1,x2,x3,x4,x5x1 =2.2662x2 =-1.7218x3 =1.0571x4 =-0.5940x5 =0.3188练习 4.3 1：A=[1 2 0;3 4 -1; 1 1 -1];B=[1 2 3;-1 0 1;-2 4 -3];A',2+A,2*A-B,A*B,A^2,A^(-1)ans =1 3 12 4 10 -1 -1ans =3 4 25 6 13 3 1ans =1 2 -37 8 -34 -2 1ans =-1 2 51 2 162 -2 7ans =7 10 -214 21 -33 5 0ans =-3.0000 2.0000 -2.00002.0000 -1.0000 1.0000-1.0000 1.0000 -2.0000 2：（1）：B=[2 4 3];B'ans =243（2）：A=[1 2 3];B=[2 4 3];A.*B,B.*Aans =2 8 9ans =2 8 93：（1）：A=[0 1 0;1 0 0;0 0 1];B=[1 0 0;0 0 1;0 1 0];C=[1 -4 3;2 0 -1;1 -2 0];A^(-1),B^(-1),X=A^(-1)*C*B^(-1) ans =0 1 01 0 00 0 1ans =1 0 00 0 10 1 0X =2 -1 01 3 -41 0 -2（2）：>> A=[1 2 3;2 2 3;3 5 1];B=[1 0 0;2 0 0;3 0 0];A^(-1),x=A^(-1)*Bans =-1.0000 1.0000 0.00000.5385 -0.6154 0.23080.3077 0.0769 -0.1538x =1 0 00 0 00 0 0练习 4.41：（1）：A=[4 2 -1;3 -1 2;11 3 0];b=[2;10;8];B=[A,b];rank(A),rank(B)ans =2ans =3（2）：A=[2 1 -1 1;3 -2 1 -3;1 4 -3 5];b=[1;4;-2];B=[A,b];rank(A),rank(B)ans =2ans =2（3）：A=[ 1 1 1 1; 1 2 -1 4;2 -3 -1 -5;3 1 2 11];b=[5;-2;-2;0];B=[A,b];rank(A),rank(B)ans =4ans =4（4）：A=[ 1 1 2 -1; 2 1 1 -1;2 2 1 2];b=[0;0;0];B=[A,b];rank(A),rank(B)ans =3ans =32：syms a;A=[-2 1 1;1 -2 1;1 1 -2];b=[-2;a;a^2];B=[A,b];rank(A),rank(B)ans =2ans =3练习4.51：（1）：A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 000 - 1.0000i（2）：A=[0 0 1;0 1 0;1 0 0];[a,b]=eig(A)a =0.7071 0.7071 00 0 -1.0000-0.7071 0.7071 0b =-1 0 00 1 00 0 1（3）：A=[4 1 -1;3 2 -6;1 -5 3];[a,b]=eig(A)a =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170b =-3.0527 0 00 3.6760 00 0 8.3766（4）：A=[1 1 1 1;1 1 -1 -1;1 -1 1 -1;1 1 -1 1];[a,b]=eig(A)a =0.5615 0.3366 0.2673 -0.7683-0.5615 -0.3366 0.0000 -0.0000-0.5615 -0.3366 -0.5345 -0.6236-0.2326 0.8125 0.8018 -0.1447b =-1.4142 0 0 00 1.4142 0 00 0 2.0000 00 0 0 2.0000（5）：A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10];[a,b]=eig(A)a =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209b =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887（6）：A=[5 6 0 0 0;1 5 6 0 0 ;0 1 5 6 0 ;0 0 1 5 6; 0 0 0 1 5 ]; [a,b]=eig(A)a =0.7843 -0.7843 -0.9860 -0.9237 -0.92370.5546 0.5546 0.0000 0.3771 -0.37710.2614 -0.2614 0.1643 -0.0000 0.00000.0924 0.0924 0.0000 -0.0628 0.06280.0218 -0.0218 -0.0274 0.0257 0.02579.2426 0 0 0 00 0.7574 0 0 00 0 5.0000 0 00 0 0 2.5505 00 0 0 0 7.4495 2：（1）：A=[0 1;-1 0];[a,b]=eig(A)a =0.7071 0.70710 + 0.7071i 0 - 0.7071ib =0 + 1.0000i 00 0 - 1.0000i>> P=orth(a),B=P'*A*P,P*P'P =-0.7071 -0.70710 - 0.7071i 0 + 0.7071iB =0 + 1.0000i 0 - 0.0000i0 - 0.0000i 0 - 1.0000ians =1.0000 0 + 0.0000i0 - 0.0000i 1.0000>> inv(a)*A*a0 + 1.0000i 000 - 1.0000i3：（1）：A=[2 0 0;0 3 2;0 2 3]; [a,b]=eig(A)a =0 1.0000 0-0.7071 0 0.70710.7071 0 0.7071b =1.0000 0 00 2.0000 00 0 5.0000>> P=orth(a),B=P'*A*P,P*P'P =-1.0000 0 -0.00000.0000 0.7071 0.7071-0.0000 -0.7071 0.7071B =2.0000 0.0000 0.00000.0000 1.0000 00.0000 0 5.0000ans =1.0000 -0.0000 0.0000-0.0000 1.0000 -0.00000.0000 -0.0000 1.0000（2）：A=[1 1 0 -1;1 1 -1 0;0 -1 1 1;-1 0 1 1];[a,b]=eig(A)a =-0.5000 0.7071 0.0000 0.50000.5000 -0.0000 0.7071 0.50000.5000 0.7071 0.0000 -0.5000-0.5000 0 0.7071 -0.5000 b =-1.0000 0 0 00 1.0000 0 00 0 1.0000 00 0 0 3.0000 >> P=orth(a),B=P'*A*P,P*P'P =-0.5000 -0.4998 -0.4783 -0.52100.5000 -0.4822 0.5212 -0.49580.5000 0.4998 -0.4964 -0.5037-0.5000 0.5175 0.5031 -0.4786 B =-1.0000 0.0000 0.0000 0.00000.0000 2.9988 -0.0362 0.03440.0000 -0.0362 1.0007 -0.00060.0000 0.0344 -0.0006 1.0006 ans =1.0000 0.0000 0.0000 -0.00000.0000 1.0000 -0.0000 00.0000 -0.0000 1.0000 0.0000-0.0000 0 0.0000 1.0000练习5.3 1: [m,v]=unifstat(1,11)m =6v =8.33332:[m,v]=normstat(0,16)m =v =256>> s=sqrt(v)s =163:x=randn(200,6);s=std(x)s =0.9094 0.9757 0.9702 0.9393 0.9272 1.09824: x=normrnd(0,16,300,1);hist(x,10)练习 5.61：x=[352 373 411 441 462 490 529 577 641 692 743];y=[166 153 177 201 216 208 227 238 268 268 274];plot(x,y,'*')4：（1）：x=[10 10 10 15 15 15 20 20 20 25 25 25 30 30 30];y=[25.2 27.3 28.7 29.8 31.1 27.8 31.2 32.6 29.7 31.7 30.1 32.3 29.4 30.8 32.8]; plot(x,y,'*')。

数学实验全部答案(精品).doc

实验十:简单的鹿群增长问题•问题一:鹿群增长模型•问题二:养老保险问题•问题三：金融公司的支付基金流动•问题四:保险金问题摘要：本篇实验报告主要是针对实验十:简单的鹿群增长问题而建立的模型。

并且将此模型的求解方法，运用到其他的类似的模型当中。

对该模型的求解，运用斧分方程组和线性代数的有关知识,通过用matlab编程,实现对矩阵的特征值和特征向量的自动求解。

以及将已知矩阵进行对角化。

并且用该模型的建模思想和求解方法，对课后的四个实验任务，分别进行了模型的建立和求解。

具体的四个实验任务如下：(1)鹿群增长模型的建立，算法编程以及程序的可行性验证；(2)养老保险问题模型的建立与求解；(3)金融公司支付基金的流动模型的建立与求解；(4)人寿保险计划模型的建立与求解；针对这几个实验任务，我分别建立了不同的数学模型，运用Matlab编程进行求解。

通过书上给出的实际数据进行了算法的可行性检验,并且通过实际数据给出了该模型的优略性评价。

问题一:鹿群增长模型问题重述：假设在一个自然生态地区生长着一群鹿,在一段时间内鹿群的增长受资源制约的因素较小。

这里所说的资源包括:有限的食物、空间、水等。

试建立一个简单的鹿群增长模型，并以适当的数据给出结果。

给出数据一：x0=0.8 ,yO=l ,al=0.3 ,a2=1.5 ,bl=0.62 ,b2=0.75 ,s=0.8; 数据二：xO=2.8 ,y0=3.4 ,al=0.4 ,a2=1.8 ,b 1=0.61 ,b2=0.72 ,s=0.7; 情况下的结果模型假设：(1)只考虑母鹿，并将其分为两组，一岁以下为幼鹿组，其余的为成年组;(2)不考虑饱和状态，即在所考虑的时间段内，种群的增长基本上是不受自然资源的制约；(3)鹿的生育数与鹿的总数成正比。

符号说明：X fl:第“年幼鹿的数量；y n：第"年成年鹿的数量；%：幼鹿的生育率；a2：成年鹿的的生育率；也：幼鹿的存活率；b2 :成年鹿的存活率；A：系数矩阵；人：矩阵A的特征值；入：矩阵A的特征值；X o：开始时幼鹿的数量；%):开始时成年鹿的数量；S:刚出生的幼鹿在哺乳期的存活率；J 代入方程⑴中，可以得到:= Au模型的建立：问题分析：根据鹿群数量增长的关系模型，建立幼鹿和成年鹿的数量关系式(观测吋间取为一年)，建立如下的线性斧分方程组：(1)问题转化为对(2)进行求解。

种群增长模型

楚雄师范学院2013年首届“雁峰杯”数学建模竞赛论文题目种群增长规律模型2013 年5月26日种群增长规律模型摘要：某个自然环境中只有一种生物的群体（生态学上称种群）生存时，人们常用Logistic模型来描述这个种群数量的演变过程。

而且一个种群就不存在相互竞争、相互依存或是弱肉强食的关系。

本文在Logistic模型基础上，根据种群数量的统计数据，建立种群指数增长模型，并利用Matlab这一数学软件对所统计的数据进行拟合，最后对模型进行分析和评价。

关键词：Logistic模型生物种群指数增长 Matlab软件一、问题重述在某个地区生长着一个种群（一类生物群落），主要依靠自然资源存活并繁殖，假设该种群单位时间的增长量与其数量成正比。

一个动物学家在2012年对的数量。

假设该地区最多只能容纳该种群2000只，请计算出该种群达到最大容量的大概时间。

二、问题分析种群的数量随时间变化而变化，根据统计数据绘出曲线图如图1。

图表 1种群数量的动态变化由图表1所绘曲线图可知种群的数量变化趋势大致成指数曲线增长，类似于其他生物种群数量的动态变化趋势。

对于生物种群的这种指数曲线的动态变化趋势，往往用Logistic模型来描述，并且根据种群的统计数据利用Matlab软件处理。

利用所得的模型对以往种群的数量进行推算预测，可检验模型的精确度，以便对模型进行改进。

三、模型假设1、假设环境环境条件允许生物种群数量有一个最大值，即环境容纳量N，当种群数量达到环境最大容纳量时，种群数量不再增长；2、种群数量的增长简单利用固有增长率r来描述；3、种群中每个个体处于同一水平，在种群增长的过程中隔天到差异如年龄结构等个不予考虑；4、在所研究地区只考虑区域内部的种群数量，不考虑种群在区域间的迁入与迁出；5、种群总数是随时间连续变化的。

四.符号说明t :时间；x：种群在t时的数量；)(tr :种群的固有增长率；N ：种群的最大数量；五.模型的建立与求解根据模型的假设，在最大容量为2000只，种群生长不受其他任何条件的限制，也就是说食物等能充分满足种群需求的情况下，种群就能充分发挥其增长能力，数量迅速增加，呈现指数增长规律，也称为“J”型增长，这种增长变化的曲线如图表2所示图表 2种群数量散点图种群在有限环境中的增长不是“J ”型，而是“S ”型，但因为在较大的空间容量，以及不考虑其它因素的情况下，种群在有限环境中的增长也可以看做是“J ”型增长，即符合“S ”型增长曲线的logistic 模型是同等的。

矩阵在数学建模中的应用举例

维普资讯
刘鹏：矩阵在数学建模中的应用举例
｛ｆｒｌ１ａｌ＋ｒｌ２ａ２＋ … ＋ｒＩｍａｍ＝Ｙｌ【，
、
ｎ＞ｍ）
Ｒ
ａ
ｙ＝
如果有向量ａ使得（ｒｉａ。＋ｒｉ＋… ＋ｒｉａ一Ｙ）达到最小，则称ａ为上述超定方程组的
Ｘｌ（ｔ）
ｇｌ（ｔ）
Ｃ１）
Ｘ２（ｔ）
ｇ２（ｔ）
Ｃ２
其中，Ａ（ｔ）＝［ａ（ｔ）］，ｘ（ｔ）＝
，ｇ（ｔ）＝
，Ｃ（ｔ）＝
● ● ●
● ● ●
Ｘ（ｔ）
Ｃ
例３：设，（ｔ），ａｉ（ｔ）（ｉ＝１，２，… ，ｎ一１）为纯量函数，ｃｊ（ｊ＝ｉ＝１，２，… ，ｎ一１）为纯量，若纯
若要求相邻槽高相差不超过４（≤４），问一批锁具中有多少不同的锁？这个问题用数学语言叙述就是设集合
Ａ＝｛（Ｘｌ，Ｘ２，…Ｘ５）ＩＸｉ∈｛１，２，… ，６｝，ｉ－１，２，… ，５；ＩＸ．一Ｘ… Ｉ≠５，ｉ＝１，２，３，４｝求Ａ中元素个数ＩＡＩ。考虑这个问题可以有许多思路：一种最自然的想法就是作组合计
ＭｉｎＺ＝ＣＸ
Ｘ
Ｓ．ｔ．ＡＸ＝Ｂ
· ５ · 楚雄币范学院学报２００６年第６期
维普资讯
楚雄师范学院学报
其中Ｘ＝。Ａ＝
ｂｌ
ｂ２
。Ｂ＝
Ｃ＝

高等教育出版社样书目录（数学类）

同济大学 10.1 2001 年 2 版
重温微积分
齐民生 39.6 2004 年 1 版
第 2 版微积分(上)
同济大学 24.9 2003 年 2 版
第 2 版微积分(下)
同济大学 23.1 2003 年 2 版
微积分学习辅导与习题选解
同济大学 28.4 2004 年 1 版
第 2 版微积分学简明教程(上)
余家荣 17.9
出版时间 2001 年 3 版 2001 年 3 版 2004 年 1 版 2003 年 1 版 2003 年 1 版 2003 年 4 版 2003 年 4 版 2003 年 2 版 2003 年 2 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 1 版 2004 年 1 版 2004 年 1 版 2003 年 3 版 1999 年 4 版 2002 年 2 版 2003 年 2 版 2004 年 1 版 2000 年 1 版 2000 年 1 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 2 版 2004 年 1 版 2003 年 3 版
高等教育出版社样书目录(数学类)
版别
教材名称
编著者单价出版时间
第4版第3版
概率论与数理统计教程概率论与数理统计教程学习辅导与习题选解
概率论与数理统计
沈恒范沈恒范盛骤
20.6 2003 年 4 版 17.6 2003 年 1 版 19.3 2001 年 3 版
概率论与数理统计习题全解指南
第 2 版数学史概论
李文林 21.0 2002 年 2 版
大学文科高等数学(第一册)
姚孟臣 11.9 1997 年 1 版

王向东数学实验课后习题解答(第二篇2.1-2.10)

数学实验课后习题解答配套教材：王向东戎海武文翰编著数学实验王汝军编写实验一曲线绘图【练习与思考】画出下列常见曲线的图形。

以直角坐标方程表示的曲线：1.立方曲线3x y=clear;x=-2:0.1:2; y=x.^3; plot(x,y)2.立方抛物线3x y=clear;y=-2:0.1:2; x=y.^3; plot(x,y) grid on3.高斯曲线2xe y-=clear;x=-3:0.1:3;y=exp(-x.^2); plot(x,y); grid on%axis equal以参数方程表示的曲线4. 奈尔抛物线)(,3223x y t y t x ===clear;t=-3:0.05:3; x=t.^3;y=t.^2; plot(x,y) axis equal grid on5. 半立方抛物线2323,()x t y t y x ===clear;t=-3:0.05:3; x=t.^2;y=t.^3; plot(x,y) %axis equal grid on6.迪卡尔曲线2332233,(30)11at at x y x y axy t t==+-=++ clear;a=3;t=-6:0.1:6; x=3*a*t./(1+t.^2); y=3*a*t.^2./(1+t.^2); plot(x,y)7.蔓叶线233222,()11at at x x y y t t a x===++- clear;a=3;t=-6:0.1:6;x=3*a*t.^2./(1+t.^2); y=3*a*t.^3./(1+t.^2); plot(x,y)8. 摆线)cos 1(),sin (t b y t t a x -=-=clear;clc; a=1;b=1;t=0:pi/50:6*pi; x=a*(t-sin(t)); y=b*(1-cos(t)); plot(x,y); axis equal grid on9. 内摆线（星形线）)(sin ,cos 32323233a y x t a y t a x =+==clear;a=1;t=0:pi/50:2*pi; x=a*cos(t).^3; y=a*sin(t).^3; plot(x,y)10. 圆的渐伸线（渐开线）)cos (sin ),sin (cos t t t a y t t t a x -=+=clear; a=1;t=0:pi/50:6*pi;x=a*(cos(t)+t.*sin(t)); y=a*(sin(t)+t.*cos(t)); plot(x,y) grid on11. 空间螺线ct z t b y t a x ===,sin ,coscleara=3;b=2;c=1; t=0:pi/50:6*pi; x=a*cos(t); y=b*sin(t); z=c*t;plot3(x,y,z) grid on以极坐标方程表示的曲线：12. 阿基米德线0,≥=r a rϕclear; a=1;phy=0:pi/50:6*pi; rho=a*phy;polar(phy,rho,'r-*')13. 对数螺线ϕa e r =clear; a=0.1;phy=0:pi/50:6*pi; rho=exp(a*phy); polar(phy,rho) 14. 双纽线))()((2cos 22222222y x a y x a r -=+=ϕclear; a=1;phy=-pi/4:pi/50:pi/4; rho=a*sqrt(cos(2*phy)); polar(phy,rho)hold onpolar(phy,-rho)15. 双纽线)2)((2sin 222222xy a y x a r =+=ϕclear; a=1;phy=0:pi/50:pi/2;rho=a*sqrt(sin(2*phy)); polar(phy,rho) hold onpolar(phy,-rho)16. 四叶玫瑰线0,2sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(2*phy); polar(phy,rho)17. 三叶玫瑰线0,3sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(3*phy); polar(phy,rho)18. 三叶玫瑰线0,3cos ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*cos(3*phy); polar(phy,rho)实验二极限与导数【练习与思考】1．求下列各极限（1）nn n)11(lim -∞→ （2）n nn n 3lim 3+∞→ （3）)122(lim n n n n ++-+∞→clear;syms ny1=limit((1-1/n)^n,n,inf)y2=limit((n^3+3^n)^(1/n),n,inf)y3=limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf)y1 =1/exp(1) y2 =3 y3 =0（4）)1112(lim 21---→x x x （5）x x x 2cot lim 0→ （6）)3(lim 2x x x x -+∞→clear; syms x ;y4=limit(2/(x^2-1)-1/(x-1),x,1) y5=limit(x*cot(2*x),x,0)y6=limit(sqrt(x^2+3*x)-x,x,inf)y4 =-1/2 y5 =1/2 y6 =3/2（7）x x x m )(cos lim ∞→ （8）)111(lim 1--→x x e x （9）x x x 11lim30-+→ clear;syms x my7=limit(cos(m/x),x,inf)y8=limit(1/x-1/(exp(x)-1),x,1) y9=limit(((1+x)^(1/3)-1)/x,x,0)y7 =1y8 =(exp(1) - 2)/(exp(1) - 1) y9 =1/32．考虑函数22),sin(3)(32<<-=x x x x f作出图形，并说出大致单调区间；使用diff 求)('x f ，并求)(x f 确切的单调区间。

04级《数学实验》B卷答案

楚雄师范学院2006—2007学年第二学期期末考试试卷《数学实验》（B ）卷评分标准答题要求：１、写出各实验的ＭＡＴＬＡＢ求解命令或程序２、除绘图题外，写出各实验的实验结果一、完成以下实验（每个实验5分，共20分）。

实验一曲线绘图1．抛物线223y x x =-+-解：clear;x=-2:0.1:2;y=-x.^2+2*x-2;plot(x,y) 5分2．圆的渐开线2(cos sin ),2(sin cos )x t t t y t t t =+=-解：clear;t=linspace(0,2*pi);x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));plot(x,y) 5分实验二极限与导数3．求极限)lim x x →∞ 解：clear;syms x;s=limit(sqrt(x^2+3*x)-x,x,1)s =1 5分4．求函数()ln ln y x =的一阶导数解：syms x;y=log(log(x));dy=diff(y,x,1)dy =1/x/log(x) 5分二、完成以下实验（每个实验5分，共20分）。

实验三级数5．求出()arctan f x x =马克劳林展开式的前５项解：clear;syms x;y=atan(x);f=taylor(y,0,5)f =x-1/3*x^3 5分６．求级数1n ∞=∑的和解：clearsyms ns=sqrt(n+2)-2*sqrt(n+1)+sqrt(n);symsum(s,n,1,inf)ans =sum((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n = 1 .. Inf) 5分实验四积分７．计算积分153cos dx x -⎰解：clear;syms x;s=int(1/(5-3*cos(x)),x)s =1/2*atan(2*tan(1/2*x)) 5分８．选用一种计算数值积分的方法，求数值积分20sin(2)x e x dx π⎰法1 复化梯形求积公式x=0:0.01:2*pi;y=exp(x).*sin(2*x);s1=trapz(x,y)s1 = -213.7824 5分法2 复化抛物线求积公式先编写M-函数文件function y=ex08(x)y=exp(x).*sin(2*x);保存后，在命令命令运行指令：s2=quad('ex08',0,2*pi)2=quad('ex08',0,2*pi)s2 = -213.7967法3 牛顿-科兹求积公式s3=quadl('ex08',0,1)s3 =-213.7967三、完成以下实验（每个实验5分，共20分）。

数学实验(MATLAB)课后习题答案

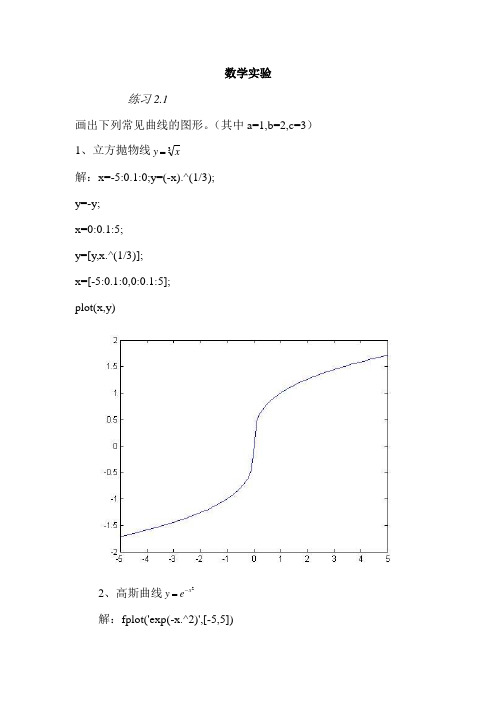
数学实验练习2.1画出下列常见曲线的图形。

（其中a=1,b=2,c=3）1、立方抛物线3xy=解：x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解：fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解：ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解：ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解：t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解：t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解：t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解：x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解：x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解：x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解：x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解：x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。

数学实验课后习题解答

数学实验课后习题解答配套教材：王向东戎海武文翰编著数学实验王汝军编写实验一曲线绘图【练习与思考】画出下列常见曲线的图形。

以直角坐标方程表示的曲线：1. 立方曲线3x y =clear;x=-2:0.1:2; y=x.^3;plot(x,y)2. 立方抛物线3x y = clear;y=-2:0.1:2; x=y.^3; plot(x,y) grid on3. 高斯曲线2xe y -=clear;x=-3:0.1:3; y=exp(-x.^2); plot(x,y); grid on%axis equal以参数方程表示的曲线4. 奈尔抛物线)(,3223x y t y t x === clear;t=-3:0.05:3; x=t.^3;y=t.^2; plot(x,y) axis equal grid on5. 半立方抛物线2323,()x t y t y x === clear;t=-3:0.05:3; x=t.^2;y=t.^3; plot(x,y) %axis equal grid on6. 迪卡尔曲线2332233,(30)11at at x y x y axy t t==+-=++ clear;a=3;t=-6:0.1:6;x=3*a*t./(1+t.^2); y=3*a*t.^2./(1+t.^2); plot(x,y)7. 蔓叶线233222,()11at at x x y y t t a x===++- clear;a=3;t=-6:0.1:6;x=3*a*t.^2./(1+t.^2); y=3*a*t.^3./(1+t.^2); plot(x,y)8. 摆线)cos 1(),sin (t b y t t a x -=-= clear;clc; a=1;b=1;t=0:pi/50:6*pi; x=a*(t-sin(t)); y=b*(1-cos(t)); plot(x,y);axis equal grid on9. 内摆线（星形线）)(sin ,cos 32323233a y x t a y t a x =+== clear; a=1;t=0:pi/50:2*pi; x=a*cos(t).^3; y=a*sin(t).^3; plot(x,y)10. 圆的渐伸线（渐开线）)cos (sin ),sin (cos t t t a y t t t a x -=+= clear; a=1;t=0:pi/50:6*pi;x=a*(cos(t)+t.*sin(t)); y=a*(sin(t)+t.*cos(t)); plot(x,y) grid on11.空间螺线ct==,,cosx=sinazttbycleara=3;b=2;c=1;t=0:pi/50:6*pi;x=a*cos(t);y=b*sin(t);z=c*t;plot3(x,y,z)grid on以极坐标方程表示的曲线：12.阿基米德线0rϕa,≥=rclear;a=1;phy=0:pi/50:6*pi;rho=a*phy;polar(phy,rho,'r-*')13. 对数螺线ϕa e r = clear; a=0.1;phy=0:pi/50:6*pi; rho=exp(a*phy); polar(phy,rho) 14. 双纽线))()((2cos 22222222y x a y x a r -=+=ϕ clear; a=1;phy=-pi/4:pi/50:pi/4; rho=a*sqrt(cos(2*phy)); polar(phy,rho) hold onpolar(phy,-rho)15. 双纽线)2)((2sin 222222xy a y x a r =+=ϕ clear; a=1;phy=0:pi/50:pi/2;rho=a*sqrt(sin(2*phy)); polar(phy,rho) hold onpolar(phy,-rho)16. 四叶玫瑰线0,2sin ≥=r a r ϕ clear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(2*phy); polar(phy,rho)17.三叶玫瑰线0arϕ=r,3sin≥clear;closea=1;phy=0:pi/50:2*pi;rho=a*sin(3*phy);polar(phy,rho)18.三叶玫瑰线0=rrϕa,3cos≥clear;closea=1;phy=0:pi/50:2*pi;rho=a*cos(3*phy);polar(phy,rho)实验二极限与导数【练习与思考】1．求下列各极限（1）n n n)11(lim -∞→ （2）n n n n 3lim 3+∞→ （3）)122(lim n n n n ++-+∞→ clear;syms ny1=limit((1-1/n)^n,n,inf)y2=limit((n^3+3^n)^(1/n),n,inf)y3=limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf)y1 =1/exp(1)y2 =3y3 =0（4）)1112(lim 21---→x x x （5）x x x 2cot lim 0→ （6）)3(lim 2x x x x -+∞→ clear;syms x ;y4=limit(2/(x^2-1)-1/(x-1),x,1)y5=limit(x*cot(2*x),x,0)y6=limit(sqrt(x^2+3*x)-x,x,inf)y4 =-1/2y5 =1/2y6 =3/2（7）x x x m )(cos lim ∞→ （8）)111(lim 1--→x x e x （9）x x x 11lim 30-+→ clear;syms x my7=limit(cos(m/x),x,inf)y8=limit(1/x-1/(exp(x)-1),x,1)y9=limit(((1+x)^(1/3)-1)/x,x,0)y7 =1y8 =(exp(1) - 2)/(exp(1) - 1)y9 =1/32．考虑函数22),sin(3)(32<<-=x x x x f作出图形，并说出大致单调区间；使用diff 求)('x f ，并求)(x f 确切的单调区间。

数学建模教材目录

数学建模教材目录(2008年10月整理）1982年以来国内正式出版的数学建模教材、译著及竞赛辅导材料，及与数学建模相关的数学实验教材（仅据各地告知的统计）：1.E.A.Bender.数学模型引论.朱尧辰、徐伟宣译，科学普及出版社，1982.2.近藤次郎.数学模型.宫荣章等译，机械工业出版社，1985.3.C.L.戴姆、E.S.艾维著.数学构模原理.海洋出版社，1985.4.姜启源.数学模型.高等教育出版社，1987.5.任善强.数学模型.重庆大学出版社，1987.6.M.Braun,C.S.Coleman,D.A.Drew,微分方程模型.朱煜民、周宇虹译，国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第一卷），1988.7.谌安琦.科技工程中的数学模型.中国铁道出版社，1988.8.江裕钊、辛培清.数学模型与计算机模拟.电子科技大学出版社，1989.9.杨启帆、边馥萍.数学模型.浙江大学出版社，1990.10.董加礼、曹旭东、史明仁.数学模型.北京工业大学出版社，1990.11.唐焕文、冯恩民、孙育贤、孙丽华.数学模型引论.大连理工大学出版社，1990.12.姜启源.数学模型（第二版）.高等教育出版社，1991.13.H.P.Williams,.数学规划模型建立与计算机应用.国防工业出版社，1991.14.李文.应用数学模型.华中理工大学出版社，1993.15.叶其孝主编.大学生数学建模竞赛辅导教材.湖南教育出版社，1993.16.寿纪麟.数学建模—方法与范例.交通大学出版社，1993.17.叶其孝.建模教育与国际数学建模竞赛.《工科数学》杂志社，1994.18.濮定国、田蔚文主编.数学模型.东南大学出版社，1994.19.欧阳亮.系统科学中数学模型.山东大学出版社，1995.20.陈义华.数学模型.重庆大学出版社，1995.21.朱思铭、李尚廉.数学模型.中山大学出版社，1995.22.蔡常丰.数学模型建模分析.科学出版社，1995.23.徐全智、杨晋浩.数学建模入门.电子科技大学出版社，1996.24.沈继红、施久玉、高振滨、张晓威.数学建模.哈尔滨工程大学出版社，1996.25.任善强、雷鸣.数学模型.重庆大学出版社，1996.26.齐欢.数学模型方法.华中理工大学出版社，1996.27.王树禾.数学模型基础.中国科学技术大学出版社，1996.28.李尚志主编.数学建模竞赛教程.江苏教育出版社，1996.29.南京地区工科院校数学建模与工业数学讨论班.数学建模与实验.河海大学出版社，1996.30.谭永基、俞文？.数学模型.复旦大学出版社，1997.31.D.Burghes.数学建模—来自英国四个行业中的案例研究，叶其孝、吴庆宝译.世界图书出版公司，1997.32.叶其孝主编.大学生数学建模竞赛辅导教材（二）.湖南教育出版社，1997.33.刘来福、曾文艺.数学模型与数学建模.北京师范大学出版社，199734.S.J.Brams,W.F.Lucas,P.D.Straffin,Jr..政治及有关模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第二卷），199735.W.F.Lucas,F.S.Roberts,R.M.Thrall.离散与系统模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第三卷），199736.H.Marcus-Roberts,M.Thompson.生命科学模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics 一书的第四卷），199737.叶其孝主编.大学生数学建模竞赛辅导教材（三）.湖南教育出版社，199838.袁震东数学建模.华东师范大学出版社，199739.贺昌政.数学建模导论.成都科技大学出版社，199840.费培之.数学模型实用教程.四川大学出版社，199841.郭锡伯、徐安农.高等数学实验课讲义.中国标准出版社,199842.H.B.Griffiths,A.Oldknow.模型数学.萧礼、张志军编译，科学出版社，199843.乐经良.数学实验.高等教育出版社，199944.萧树铁主编.数学实验.高等教育出版社，1999.45.李尚志.数学实验.高等教育出版社，1999.46.谢云荪等.数学实验.科学出版社，199947.吴翊等.数学建模的理论与实践.国防科技大学出版社，199948.周义仓.数学建模实验.西安交通大学出版社，199949.朱道元.数学建模精品案例.东南大学出版社，199950.雷功炎.数学模型讲义.北京大学出版社，199951.朱建青.数学建模.解放军出版社，199952.边馥萍.工科基础数学实验.天津大学出版社，199953.贾晓峰.微积分与数学模型.高等教育出版社，199954.赵静等.数学建模与数学实验，高等教育出版社，施普林格出版社，200055.龚劬,、刘琼荪、何中市、傅鹂.数学实验.科学出版社，200056.白其峥.数学建模案例分析.海洋出版社，200057.蔡锁章等.数学建模原理与方法.海洋出版社.200058.杨学桢.数学建模方法.河北大学出版社，200059.王庚.实用计算机数学建模.安徽大学出版社，200060.魏平等.数学实验.吉林人民出版社，200061.钟尔杰.实用数值计算方法.高等教育出版社，200162.杨振华、郦志新.数学实验科学出版社，200163.叶其孝主编.大学生数学建模竞赛辅导教材（四）.湖南教育出版社，200164.全国大学生数学建模竞赛组委会.大学数学建模的理论与实践–2001中国大学生数学建模夏令营.湖南教育出版社，200165.钟尔杰.数学实验简明教程.电子科技大学出版社，200166.何万生、李万同.数学模型与建模.甘肃教育出版社，200167.何万生.数学模型与建模.甘肃教育出版社，2001.68.胡良剑、丁晓东、孙晓君.数学实验——使用MATLAB.上海科学技术出版社，200169.张兴永.数学建模简明教程.中国矿业大学出版社，2001.70.宋世德、郭满才、王经民、边宽江等..数学实验.高等教育出版社，200271.杨振华、郦志新.数学实验.科学出版社，200272.刘新平、魏暹逊等.数学建模导论.陕西师范大学出版社，200273.何文章、宋作忠.数学建模与实验.哈尔滨工程大学出版社，200274.刘来福、曾文艺.数学模型与数学建模.北京师范大学出版社，200275.周晓阳、谢松发、梅正阳.数学实验与MATLAB.华中科技大学出版社，200276.袁震东、蒋鲁敏、束金龙.数学建模简明教程.华东师范大学出版社，200277.刘承平.数学建模方法.高等教育出版社，200378.徐全智、杨晋浩.数学建模.高等教育出版社，200379.姜启源.、谢金星、叶俊.数学模型（第三版）.高等教育出版社，200380.魏贵民、郭科.理工数学实验.高等教育出版社，200381.万福永、戴浩晖.数学实验教程.科学出版社，200382.朱道元.数学建模案例精选.科学出版社，2003.83.李秀珍、庞常词、韦忠礼、黄福同.数学实验.中国农业科学技术出版社，200384.谢兆鸿、范正森、王艮远.数学建模技术.中国水利水电出版社，200385.赵红革.高等数学教材（含数学实验）.经济日报出版社，200386.蔡锁章等.数学建模.林业出版社，.200387.薛长虹等.大学数学实验.西南交通大学出版社，200388.朱建青.数学建模方法.郑州大学出版社，200389.杨瑞琰等.数学建模入门.中国地质大学出版社，200390.孙卫、张宇萍.高等数学实验.西北工业大学出版社，200391.杨策平.经济数学模型分析.中国地质大学出版社，200392.袁震东等.数学建模方法.华东师范大学出版社，200393.赫孝良、戴永红、周义仓.数学建模竞赛赛题简析与论文点评.西安交通大学出版社，200394.李尚志等.数学实验（第二版）.高等教育出版社，200495.王向东.数学实验.高等教育出版社，200496.李亚杰.数学实验.高等教育出版社，200497.刘琼荪等.数学实验.高等教育出版社，200498.张国权.数学实验.科学出版社，200499.马知恩、周义仓.传染病动力学的数学建模与研究.科学出版社，2004100.杨静化、韩可勤.医药数学建模教程.科学出版社，2004101.颜文勇.高等数学及实验.科学出版社，2004102.赵红革.经济数学教材（含数学实验）.经济日报出版社，2004103.何文章,、桂占吉、贾敬.大学数学实验.哈尔滨工程大学出版社，2004104.刘振航.数学建模.中国人民大学出版社，2004105.王兵团.数学建模基础.清华大学出版社，2004106.李继玲等.数学实验基础.清华大学出版社，2004107.李继玲、沈跃云、韩鑫.数学实验基础.清华大学出版社，2004108.薛毅.数学建模基础.北京工业大学出版社，2004109.郎艳怀等.经济数学方法与模型教程.上海财经大学出版社，2004110.甘筱青、陈涛、陈钰菊.数学建模教育及竞赛.江西高校出版社，2004111.赵东方.数学实验与数学模型.华中师范大学出版社，2004112.李林、周永正、煮祖庆、詹棠森.数学实驼与数学建模教程.中国林业出版社,2004113.王冬琳.数学建模及实验.国防工业出版社,2004114.张珠宝等.数学实验与数学建模.高等教育出版社，2005115.边馥萍、侯文华、梁冯珍.数学模型方法与算法.高等教育出版社，2005116.苏海容副主编.数学模型与数学实验（高职高专用书）.高等教育出版社，2005117.韩中庚.数学建模方法及其应用.高等教育出版社，2005118.杨启帆等.数学建模.高等教育出版社，2005119.唐焕文、贺明峰.数学模型引论（第三版）.高等教育出版社，2005120.阮晓青、周义仓.数学建模引论.高等教育出版社，2005121.王正东、尹强.数学软件与数学实验.科学出版社，2005122.宋来忠主编.数学建模与实验.科学出版社，2005123.焦光虹.数学实验.科学出版社，2005124.孟军、尹海东.农业数学实验.科学出版社，2005125.F.R.Giordano,M.D.Weir,W.P.Fox.数学建模（第三版）.叶其孝、姜启源等译.机械工业出版社，2005126.M.M.Meerschaert.数学建模–方法与分析（第二版）.刘来福等译.机械工业出版社，2005127.吴建国主编.数学建模案例精编.中国水利水电出版社，2005128.马新生、陈涛、陈钰菊、廖川荣.高等数学实验教材.中国科技出版社，2005129.杨启帆等.数学建模竞赛——浙大学生获奖论文点评（1999-2004）.浙江大学出版社，2005130.姜启源.、邢文训、谢金星、杨顶辉.大学数学实验.清华大学出版社，2005131.谢金星、薛毅.优化建模与LINDO/LINGO软件.清华大学出版社，2005132.柏宏斌、陈德勤.数学实验.四川大学出版社，2005133.谭永基、蔡志杰、俞文鮆.数学模型.复旦大学出版社，2005134.熊启才.数学模型方法及应用.重庆大学出版社，2005135.杨尚俊.数学建模简明教程.安徽大学出版社，2005136.刘锋.数学建模.南京大学出版社，2005137.萧树铁主编.数学实验（第二版）.高等教育出版社，2006138.李继成、朱旭、李萍.数学实验.高等教育出版社，2006139.谭永基等.经济、管理数学模型案例教程.高等教育出版社，2006140.杨启帆等.数学建模案例集.高等教育出版社，2006141.胡良剑、孙晓君.MATLAB数学实验.高等教育出版社，2006142.万福永、戴浩晖、潘建瑜.数学实验教程-MATLAB版.科学出版社，2006143.焦光虹.数学实验.科学出版社，2006144.董臻圃主编.数学建模方法与实践.国防工业出版社，2006145.陈汝栋、于延荣.数学模型与数学建模.国防工业出版社，2006146.张兴永、朱开永.数学建模.煤炭工业出版社，2006147.曹喜望.管理科学中的数学模型.北京大学出版社，2006.148.王兵团.数学实验基础（修订本）.清华大学出版社，2006149.湖北省大学生数学建模竞赛专家组.数学建模（本科册）.华中科技大学出版社，2006150.张学山、江开忠、李路.高等数学实验.华东理工大学出版社，2006151.赵红革、王为洪等.高等数学教材（含数学实验）.北京交通大学出版社，2006152.李伯德.数学建模方法.甘肃教育出版社，2006153.黄世华.数学建模基础教程.甘肃教育出版社,，2006154.任善强、雷鸣.数学模型（第二版修订版）.重庆大学出版社，2006155.刘新平、陈斯养等.全国大学生数学建模竞赛获奖论文集.陕西师范大学出版社，2006156.李辉来、刘明姬等.数学实验.高等教育出版社，2007157.姜启源、谢金星主编.数学建模案例选集.高等教育出版社，2007158.全国大学生数学建模竞赛组委会.数学建模的实践—2006年全国大学生数学建模夏令营论文集.高等教育出版社，2007 159.赵静、但琦主编.数学建模与数学实验（第三版）.高等教育出版社，2007160.戴明强、李卫军、杨鹏飞.数学模型及其应用.科学出版社，2007161.袁新生.lingo和excel在数学建模中的应用.科学出版社，2007162.韩中庚.数学建模竞赛获奖论文精选与点评.科学出版社，2007163.高隆昌、杨元.数学建模基础理论.科学出版社，2007164.彭放等、数学建模方法.科学出版社，2007165.肖海军.数学实验基础.科学出版社，2007166.蔡光兴、金裕红.大学数学实验.科学出版社，2007167.江世宏.MATLAB语言与数学实验.科学出版社，2007168.高等教育出版社2008年12月赵东方.数学模型与计算.科学出版社，2007169.冯杰等.数学建模原理与案例.科学出版社，2007170.宋世德、郭满才.数学实验.中国农业出版社，2007171.李志林、欧宜贵.数学建模及典型案例分析.化学工业出版社，2007172.吴礼斌、李柏年.数学实验与建模.国防工业出版社，2007173.李宏艳、王雅芝.数学实验（第二版）.清华大学出版社，2007174.薛毅、陈立萍.统计建模与R软件.清华大学出版社，2007175.陈理荣.数学建模导论.北京邮电大学出版社，2007176.周义仓、赫孝良.数学建模实验（第二版）.西安交通大学出版社，2007177.赵临龙.全国数学建模竞赛—高职高专大学生获奖论文点评（2002-2006年）.中国人民大学出版社，2007 178.罗万成等.大学生数学建模案例精选.西南交通大学出版社，2007179.杨桂元等.数学模型应用实例.合肥工业大学出版社，2007180.薛南青.数学建模基础理论与案例精选.山东大学出版社，2007181.数学建模走进中学课堂（VCD）.中央广播电视大学音像出版社，2007182.贾晓峰、魏毅强、王希云.微积分与数学模型.高等教育出版社.，2008183.孙浩等.数学建模简明教程.高等教育出版社，2008184.徐全智.数学建模（第二版）.高等教育出版社，2008185.陈恩水、王峰.数学建模与数学实验.科学出版社2008186.汪晓银、邹庭荣.数学软件与数学实验.科学出版社，2008187.刘焕彬等.数学模型与实验.科学出版社，2008188.王庚、王敏生.现代数学建模方法.科学出版社，2008189.王树禾.数学模型选讲.科学出版社，2008190.陶凤燕等.对应分析数学模型及其应用.科学出版社，2008191.陆志奇、李静.竞争数学模型的理论研究.科学出版社，2008192.朱道元.数学建模.机械工业出版社，2008193.李秀珍等.数学实验.机械工业出版社，2008194.刘三阳主编.数学建模.电子工业出版社，2008195.刘保东等.数学建模与数学实验.人民邮电出版社，2008196.重庆邮电大学数学建模组.数学建模素材选编.人民邮电出版社，2008197.王文波.数学建模及其基础知识详解.武汉大学出版社，2008198.张圣勤.数学建模与数学实验.复旦大学出版社，2008199.任善强、雷鸣、肖剑、周寅亮.数学模型.重庆大学出版社，2008200.王连堂主编.数学建模.陕西师范大学出版社，2008201.肖华勇.基于MATLAB和LINGO的数学实验.西北工业大学出版社，2008202.朱旭、李换琴、籍万新.MATLAB与基础数学实验.西安交通大学出版社，2008203.雷功炎.数学模型八讲——模型、模式与文化.北京大学出版社，2008204.叶其孝主编.大学生数学建模竞赛辅导教材（五）.湖南教育出版社，2008205.李大潜主编.中国大学数学建模竞赛(第三版).高等教育出版社,2008.《工程数学学报》编辑部:地址：西安交通大学理学院;邮编： 710049 ;电话： (029)82667877。

数学实验答案完整版

173、>> syms a b>> a=2.3;b=4.89;>> sqrt(a^2+b^2)/abs(a-b)ans =2.08644、>> syms x>> x=pi/3;>>sqrt(sin(x)+cos(x))/abs(1-x^2)ans =12.09625、>> syms x>> x=1.23;>> atan(x)+sqrt(log(x+1))ans =1.78376、>> syms x>>x=-2.1;>> 2-3^x*log(abs(x))ans =1.92617、>> syms x y>>x=0:0.2:2;y=2*sqrt(x);>> plot(x,y,'b.-')8、>> syms x y>> x=-20:0.2:-15;y=log(abs(x+10)); >> plot(x,y,'mx-')9、>> syms x y;>> x=-10:0.2:10;y=sin(x/2-pi/2); >> plot(x,y,'r+--')10、>> syms x y>> x=0:0.2:4*pi;y=sin(2*x+pi/3); >> plot(x,y,'mo-.')11、>> syms x y1 y2>> x=0:pi/50:2*pi;y1=cos(3*sqrt(x));y2=3*cos(sqrt(x));>>plot(x,y1,'cx-',x,y2,'r*--')12、>> syms x y1 y2 y3;>>x=-2:0.1:2;y1=x.^2;y2=x.^3;y3=x.^4;plot(x,y1,x,y2,x,y3);13、>> syms x y t z>> t=0:1/50:2*pi;>> x=t^2;y=sin(t);z=t;>> stem3(x,y,z)14、>> syms x y u v z>> u=0:pi/50:2*pi;v=0:pi/50:2*pi;>>x=(1+cos(u)).*cos(v);y=(1+cos(u)).*sin(v);z=sin(u);>> plot3(x,y,z)15、>> syms x y>> y=sin(2^0.5*x)/sqrt(1-cos(x));>> limit(y,x,0,'right')ans =216、>> syms y x>> y=(1/3)^(1/(2*x));>> limit(y,x,0,'right')ans =17、>> syms x y>> y=(x*cos(x))/sqrt(1+x^3);>> limit(y,x,+inf)ans =18、>> syms x y>> y=((x+1)/(x-1))^(2*x);>> limit(y,x,+inf)ans =exp(4)19、>> syms x y>> y=(1-cos(2*x))/(x*sin(x));>> limit(y,x,0)220、>> syms x y>> y=(sqrt(1+x)-sqrt(1-x))/x;>> limit(y,x,0)ans =121、>> syms x y>> y=(x^2+2*x+1)/(x^2-x+2);>> limit(y,x,+inf)ans =122、>> syms x y>> y=(2*x-1)^5+atan(x);>> diff(y)ans =10*(2*x - 1)^4 + 1/(x^2 + 1)23、>> syms y x>> y=(x*tan(x))/(1+x^2);>> diff(y)ans =tan(x)/(x^2 + 1) + (x*(tan(x)^2 + 1))/(x^2 + 1) - (2*x^2*tan(x))/(x^2 + 1)^2 24、>> syms y x>> y=exp^(-3*x)*tan(x)；>> y=exp(-3*x)*tan(x)；y =exp(-3*x)*tan(x)>> diff(y)ans =exp(-3*x)*(tan(x)^2 + 1) - 3*exp(-3*x)*tan(x)25、>> syms x y>> y=(1-x)/(1+x);>> diff(y,x,2)ans =2/(x + 1)^2 - (2*(x - 1))/(x + 1)^3>> syms x y>> y=2*log(x)+sin(pi*x/2)^2;>> dxdy=diff(y)2/x + pi*cos((pi*x)/2)*sin((pi*x)/2)zhi=subs(dxdy,1)zhi =226、>> syms x y>> y=(1-x)/(1+x);>> diff(y,x,2)ans =2/(x + 1)^2 - (2*(x - 1))/(x + 1)^327、>> syms x y>> y=((x-1)^3*(3+2*x)^2/(1+x)^4)^0.2;>> diff(y)ans =(((8*x + 12)*(x - 1)^3)/(x + 1)^4 + (3*(2*x + 3)^2*(x - 1)^2)/(x + 1)^4 - (4*(2*x + 3)^2*(x -1)^3)/(x + 1)^5)/(5*(((2*x + 3)^2*(x - 1)^3)/(x + 1)^4)^(4/5))28、>> f='-3*x^4+4*x^3-1'; >> [x,y]=fminbnd(f,-inf,inf)x =NaNy =NaN>> f='3*x^4-4*x^3+1';>> [x,y]=fminbnd(f,-inf,inf)x =NaNy =NaN29、>> f='(x-1)*x^0.6';>> [x,y]=fminbnd(f,-1,5)x =0.3750y =-0.3470>>>> f='-(x-1)*x^0.6';>> [x,y]=fminbnd(f,-1,5)x =4.9999y =-10.505930、>> syms x y>> y=log(3*x)-2*sin(x);>> int(y)ans =2*cos(x) - x + x*log(3) + x*log(x)31、>> syms x y>> y=exp(x)*sin(x)^2;>> int(y)ans =-(exp(x)*(cos(2*x) + 2*sin(2*x) - 5))/10 32、>> syms x y>> y=x*atan(x)/(1+x)^0.5;>> int(y)Warning: Explicit integral could not be found.ans =int((x*atan(x))/(x + 1)^(1/2), x)33、>> syms x y>> y=1/exp(x^2)*(2*x-cos(x));>> int(y)Warning: Explicit integral could not be found.ans =int(exp(-x^2)*(2*x - cos(x)), x)34、>> syms x y>> y=exp(-x)*(3*x+2);>> int(y,0,1)ans =5 - 8*exp(-1)35、>> syms y x>> y=(x^2+1)*acos(x);>> int(y,0,1)ans =11/936、>> syms x y>> y=(cos(x)*log(x+1));>> int(y,0,1)Warning: Explicit integral could not be found.ans =int(log(x + 1)*cos(x), x = 0.1) 37、>> syms y x>> y=(1/(x^2+2*x+2));>> int(y,-inf,inf)ans =pi38、>> syms x y>> y=x^2*exp(-x);>> int(y,0,+inf)ans =2。

王向东数学实验课本(可编辑)2-10

实验十周期函数【实验目的】1．了解几周期函数的基本概念。

2．了解周期函数经过四则运算、复合运算、求导运算、积分运算后的周期性。

3．学习掌握MATLAB 软件有关的命令。

【实验内容】从图形上观测六个三角函数的周期性【实验准备】1．周期函数的基本概念函数)(x f 是以T 为周期的周期函数是指对任何x ，有)()(x f T x f =+.使得上式成立的最小正数T 称为函数的最小正周期。

2．周期函数的四则运算若)(),(x g x f 都是周期函数，一般地，他们的和（差）积商都未必再是周期函数。

例如][)(x x x f -=在),(+∞-∞以11=T 为最小正周期，x x g sin )(=在),(+∞-∞以π=2T 为最小正周期，但)()(x g x f +并非周期函数。

事实上，对任意实数0>a ，总有.0)0()0()()(=+>+g f a g a f但我们有如下具有一般意义的结论：若)(),(x g x f 都是周期函数，具有正周期21,T T ，且21T T 为有理数，则 )0)(()()(),()(),()(≠±x g x g x f x g x f x g x f 仍是周期函数。

事实上，设q p qpT T ,,21=是互质的自然数，则可以证明21pT qT T ==是)(),(x g x f 的周期，从而是经过四则运算后函数的周期。

3．周期函数的最小正周期一般说来，周期函数未必有最小正周期。

例如，常值函数c x f =)(显然是没有最小正周期的，事实上，容易证明任何实数T 都是)(x f 的周期。

然而，非常值的周期函数也未必有最小正周期，例如⎩⎨⎧-=是理数，是有理数x x x g 1,1)(由于有理数与有理数（无理数）之和必为有理数（无理数），因此任何一个有理数都是)(x g 的周期，显然)(x g 没有最小正周期。

但我们有如下具有普遍意义的结论：非常值函数M x x f y ∈=),(，如果在M 的某聚点处有一单边有限或无限的极限，则)(x f 必有最小正周期。

自-王向东数学实验课本3-12

实验十二刀具寿命的测定【实验目的】１.了解数理统计中数据描述和分析的基本概念和方法。

２.通过对实际数据的分析、统计,初步培养统计推断解决问题的建模思想。

３.学习掌握用MAＴLAB命令进行参数估计、假设检验和统计推断问题的求解。

【实验内容】一道工序用自动化车床连续加工某种零件，由于刀具损坏等原因，该工序会出现故障,工序出现故障是完全随机的,假定在生产任一零件时出现故障的机会均相同。

工作人员通过检查零件来确定工序是否出现故障。

现积累有100次刀具故障记录,故障出现时该刀具完成的零件数如下表:试确定刀具的平均寿命，同时判断该刀具出现故障时完成的零件数属于何种分布。

【实验准备】在现代社会中，数据是事物现象的反映，是科学推断的依据,起着至关重要的作用。

由于各种随机因素的影响，实验数据往往带有一定的误差，这时需要从数据中分离出随机因素的成分，从而挖掘出事物规律性的成分,以此对所研究总体的性质作出推测性的判断。

进行这样的分析建立在收集大量数据的基础之上，称为统计分析。

1.概率统计的基本概念总体是人们研究对象的全体,又称为母体，而组成总体的每个单元叫做个体。

任何一个总体都可以用一个随机变量来描述它。

所以,总体就是一个带有确定概率分布的随机变量，常用X ,Y ,Z 等表示总体。

一般情况下，总体的数目非常大，对于总体X 分布规律进行研究就必须对总体抽样观察，并分析推断，这种研究过程称为抽样。

从总体X 中，随机地抽取n 个个体1x ,2x ,…，n x (例如在１0000件灯管中抽取10０件检查次品数量），这样取得的（1x ，2x ,…，n x )称为总体X 的一个样本容量为n 的样本或子样。

统计推断就是根据样本来对总体进行分析、推断。

通常的作法，依据某种理由或经验来假定总体服从已知形式的概率分布，只要由样本来推断总体概率分布中的若干参数。

所以样本的获取会直接影响统计推断的结果,理想的样本是随机、相互独立且与总体同分布。

实验数学必修一练习册答案

参考答案1.1.1集合的含义与表示 A 组1.C2.A3.A4.D5.D6.B7.{1,1}-8.69.(1){31,}x x k k N =+∈ (2){32,}x x k k Z =+∈10.(1) {1,0,3}-；2{(230)}x x x x --= (2){3,4,5,6}；{27}x Z x ∈<<11.1a =，元素为1-；0a =，元素12- 12. 1- B 组1.D2.C3.74.(1)是；(2)是 C 组1.B2.D3.{56}a a <≤4.41 1.1.2集合之间的关系1.B2.A3.B4.C5.B6.C7.1-或28.C A B ⊆=9.4个 10.1{0,2,}3-11．11a b =-⎧⎨=⎩或11a b =⎧⎨=⎩或01a b =⎧⎨=-⎩ 12.31,42d q =-=-B 组1.A2.C3.64.(,1]-∞-C 组1.B2.C3. A B4.401.1.3集合的基本运算（一）A 组 1.A 2.A 3.D 4.C 5.B 6.C 7.{0} 8.{2,4} 9.1或0 10.(1)2a = (2){4,2,4,5,25}- 11.a=-1 b=3 12.(1) {a| a≤-1或a=1} (2)a=1 B 组 1.D 2.D 3.4 4.55C 组 1.C 2.D 3.{a|2<a<3} 4.A={1,3,5,9} 1.1.3集合的基本运算（二）A 组 1. A 2.C 3.C 4.D 5.C 6.A 7.{3,1,3,4,6}- 8.{0x x <或4}x ≥ 9.1{1,}2-10.6m = 11. (){2A B x x ⋃=≤或10}x ≥；(A ){23B x x ⋂=<<或710}x ≤<12.不存在.B 组 1.C 2.D 3.{2}a a ≥- 4.(){1,2,6,7}A B ⋂=，(A )⋃()B {1,2,6,7}=，()A B φ⋃=，(A )⋂()B φ=.结论：()A B ⋂=(A )⋃()B ，()A B ⋃=(A )⋂()BC 组 1.A 2.B 3.2k <或6k > 4.3{2a a ≤-或1}a ≥-1.2.1函数的概念A 组 1.C 2.A 3.D 4.B 5.B 6.A 7.{0,1,3}- 8.110.(1)0,0,0 (2)()()0f x f x --= 11.21122x x + 12.2008.5 B 组 1.D 2.A 3.5 4.2p q + C 组 1.C 2.C 3.9 4.2()2x f x x =+ 1.2.2函数的表示法（一） A 组选择题1.B2. A3.C4.C5.B6.A 填空题7.(4,2)-，(2,1)- 8. 1,10,()1,0 2.2x x f x x x +-≤≤⎧⎪=⎨-<≤⎪⎩ 9.(1,1)-解答题10.()27f x x =+ 11.(略)12. 600 2.5600 2.51502.53.50 2.5 3.532550 3.5 6.550 3.5 6.5tt t x t v t t t t ≤≤≤≤⎧⎧⎪⎪=<≤=<≤⎨⎨⎪⎪-<≤<≤⎩⎩B 组1.C2.C3.34.解析式2(2)2y x lx π=-++，定义域{0}2lx x π<<+ C 组1.C2.B3.1233x x-- 4.221y x x =-- 1.2.2函数的表示法（二）A 组1.D2.C3. C4.B5.C6..[2,1)(1,2]-⋃7.[0,1]8.1x x + 9.(1)(,2)(2,)-∞⋃+∞ (2)(,1)(1,)-∞⋃+∞ 10.[0,1] 11.[2,2]- B 组 1.C 2.D 3.17(,]8-∞ 4.[,]b b - C 组 1.B 2.B 3.21x x -+ 4.()()2F x F x +-= 1.3.1函数的单调性与最值（一） A 组1.B2. A3.C4.C5.D6.B7.1(,)2-∞- 8.[2,)+∞ 9.3(,3)210.(略) 11.在区间(0,1]上单调递减，在[1,)+∞上单调递增 12.(略) B 组1.C2.D3.(,3]-∞-4.单调递减区间(,)-+∞b 和(,)-∞-b C 组1.C2.B3.[2,)-+∞4.[3,)+∞ 1.3.1函数的单调性与最值（二）A 组 1.B 2.A 3.A 4.C 5.B 6.C 7.(,1)(0,)-∞-⋃+∞8．23(1)()4f a a f -+≤ 9.1- 10.(0,2]递减，[2,)+∞递增；递减，(,)-∞+∞递增.11．(,1]-∞-，[0,1]递减；[1,0],[1,)-+∞递增. 12.(1)最大值37，最小值1 (2)5a ≥或5a ≤-B 组 1.C 2.B 3.1[,)2+∞ 4.221(0)()1,(01)22(1)t t g t t t t t ⎧+<⎪=≤≤⎨⎪-+>⎩C 组 1.B 2.C 3.3[,3]24.最大值2，最小值2- 函数的奇偶性1.3.2函数的奇偶性（一） A 组1.D2.D3.B4.C5.A6.B 7．(1)(2)(3)f f f <-<- 8.26- 9.1,03a b == 10.(1) 偶函数（2）奇函数11.（1）非奇非偶函数（2）非奇非偶函数（3）奇函数（4）奇函数 12. ()(1)f x x x =+B 组 1.C 2.C 3.0 4(1)(略) （2）最大值为1，最小值为3- C 组1. A2.A3.1y x=4.（1）1,1,0a b c === （2）(,1]-∞-单调递增， [1,0)-单调递减 1.3.2函数的奇偶性（二）A 组 1.B 2.C 3.A 4.A 5.C 6.B 7.(0,2) 8.1 9.010.(1)证明：(略) (2)3142x -<≤- 11.[0,1) 12. (1)()()f a f b > (2) 15[,]24- B 组 1.D 2.C 3.3(2)()(1)2f f f <-<- 4.221(),()11xf xg x x x ==--，定义域关于原点对称的函数一定可写成一个奇函数与一个偶函数的和.C 组. 1.B 2.B 3.km 4.(1)2()1x f x x =+ (2)(略) (3)1(0,)2函数基础测试题1.D2.A3.C4.D5.C6.A7.B8.B9. A10.23 11.[2,1)(1,)-⋃+∞ 12.(,2)(1,0)-∞-⋃- 13.[4,0)(0,1]- 14. (,3]-∞ 15. (1) 21()2f x x x =-+ (2)奇函数 16. 0a <时，最小值为222a a -+；4a >时，最小值为21018a a -+；04a ≤≤时，最小值为22a -.集合与函数单元检测题1.C2.D3.B4.B5.D6.B 7C 8.A 9.D 10.D 11.D 12.D 13.31[,)22-14.1 15.[0,)+∞ 1611{0,,}2317.(1)R ；(2){13x x <<或57}x <<；(3) {1,35x x x ≤≤≤或7}x ≥ 18.(1){1}x x ≠± (2)偶 (3)(略) 19.{2,1}--或{2,0}-20.2(04)8(48)242(812)x x y x x x ≤≤⎧⎪=<<⎨⎪-≤≤⎩21.13a b =-⎧⎨=⎩或10a b =⎧⎨=⎩22.(1)(略) (2)(略) (3)(略) (4)(0,3)§2．1．1A 组1．D ；2．B ；3．B ；4．C ；5．A ；6．B ；7. 218x -； 8．362；9．1；10．4， 51，32，827;11．（Ⅰ）4a ；（Ⅱ）32nm ;12． (Ⅰ)(Ⅱ) B 组1．B ；2．D ；3．9.7385；4．（Ⅰ）23.a （Ⅱ）n n b a )(-+n n b a )(+=⎩⎨⎧-.,2,,2为偶数为奇数n a n aC 组1．B ；2．A ；3．19; 4．（Ⅰ）13x -;（Ⅱ）0.§2．1．2A 组1．C; 2．C;3．D;4．A; 5．A;6．C; 7. 1,12⎛⎫⎪⎝⎭;8. (],2-∞;9. 28；10．略 11． (Ⅰ)2x <；(Ⅱ)当112a <<时,4x >-;当1a >时，4x <-.12． ab b a a b a b > B 组1．B; 2．1,2⎛⎫+∞⎪⎝⎭;3．10,4⎛⎤ ⎥⎝⎦;4．(Ⅰ)2,13⎛⎫⎪⎝⎭; (Ⅱ)略 C 组1．D; 2．D;3．递增; 4．当1a >时，值域[),a +∞；当01a <<时，值域(]0,a§2．1．3A 组1．A ；2．A ；3．C ；4．B ；5．A ；6．A ；7．1333aa a >>;8．()1311%xy =+;9．{}|1x x <10． 32a =或12a =.11．R ,(],81-∞,(],1-∞是增区间,(]1,+∞ 是减区间12．2,53⎛⎫⎪⎝⎭B 组1．D ；2．D ； 3．(]0,1; 4．（Ⅰ）{}|0x x ≠；（Ⅱ）奇函数;略C 组1． D ；2．C ；3．01k <<; 4．略§2．2．1A 组1．D ；2．D ；3．B ；4．C ；5．C ；6．C ；7． 2；8．2a -；9．1；10．3；11．（Ⅰ）2x =.（Ⅱ）x =（Ⅲ）8x =.12．0.8266.B 组1．B ；2．A ；3．3a ; 4．4. C 组1．B ；2．A ；3．1; 4．略§2．2．2A 组1．B ；2．C ；3．A ；4．A ；5．A ；6．B ；7．()3,1; 8．(),2.5-∞，(),5-∞;9．3;10．（Ⅰ）22log 3.4log 3.8<（Ⅱ）0.50.5log 1.8log 2.1>.（Ⅲ）当1a >时， log 5.1log 5.9a a <；当01a <<时，log 5.1log 5.9a a >. 11．（Ⅰ）{}|0x x ≠.（Ⅱ）{}|1x x >. 12．（Ⅰ）略（Ⅱ）减函数 B 组1．B ；2．C ；3．241; 4． 11log log log log b a a ba b b b a >>> C 组1.B ；2．B ；3．（Ⅰ）304k ≤≤; （Ⅱ）34k ≥ 4．（Ⅰ）当1a >时，定义域为(),0-∞，值域为(),0-∞；当01a <<时，定义域为()0,+∞，值域为()0,+∞.（Ⅱ）∵1a >时，1xt a =-在(),0-∞上单调递减，log a y t =关于t 单调递增， ∴()log 1xa y a =-在(),0-∞上单调递减.∵当01a <<时，1xt a =-在()0,+∞上单调递增，而log a y t =关于t 单调递减，∴()log 1xa y a =-在()0,+∞上单调递减.§2．2．3A 组1．D ；2．C ；3．A ；4．D ；5．B ；6．C ；7．60.70.7log 60.76<<；8．12a <<；9．()1,-+∞ 10．（Ⅰ）即定义域为R ;（Ⅱ）()f x 是定义在R 上的奇函数; （Ⅲ）()f x 在()0,+∞上为减函数,()f x 在(),0-∞上也为减函数. 11．（Ⅰ）定义域是()1,3-; (Ⅱ)增区间是()1,1-，减区间是[]1,3; （Ⅲ）当1x =时,y 取得最大值1.12．（Ⅰ）函数()f x 的定义域为()(),,b b -∞-⋃+∞;（Ⅱ）奇函数; （Ⅲ）函数()f x 在区间(),-∞+∞上单调递减B 组1．A ；2．D ； 3．()21,0,3⎛⎫+∞⋃ ⎪⎝⎭; 4．12a <<C 组1.A ；2．B ；3．()10,2,2⎛⎫⋃+∞ ⎪⎝⎭;4．（Ⅰ）当1a >时，定义域为()0,+∞；当01a <<时，定义域为(),0-∞. （Ⅱ）当1a >时，()f x 在（0，+∞）上为增函数. 当01a <<时，()f x 在（－∞，0）上为增函数. （Ⅲ）01a <<§2．3．1A 组1．D ；2．C ；3．B ；4．C ；5．B ；6．D ；7．二;8．0x <;9．2aa a a a a a >>10．1x >;11．1t =±;12．23a <B 组1．B ；2．B; 3．b a c >>; 4．()()1,,0+∞⋃-∞C 组1．B ；2．B ；3．()()0,1,0⋃-∞; 4．（Ⅰ）定义域为R ;（Ⅱ）0y ≥;（Ⅲ）偶函数. （Ⅳ）在()0,+∞上单调递增;在(),0-∞上单调递减. （Ⅴ）其图象如图所示基础训练1．D ；2．C ；3．A ；4．C ；5．A ；6．D ；7.B ； 8．C ；9．A ；10．B;3252311.2,12.log 2,13.[,8],14.{|1}432a a a <<<-或 15.（Ⅰ）1{|1}3y y -≤<(Ⅱ){|11}y y y ><-或 16.（Ⅰ）当1a >，定义域{|1}x x <值域{|1}y y <； (Ⅱ)减函数；121917.(1)1,(2)()log (3)18x a f x m x +=-=<-- 综合训练一、选择题156101112BDBABBABAC CA ---二、填空题15113.,2,14.0,15.4m a a a =<<≥≤或1三、解答题17.（Ⅰ）21,()m f x x ==.(Ⅱ)12a <<; 18.77[,]9819.（Ⅰ）2()()1x x af x a a a -=--,当01a a >≠且时1m <≤Ⅱ)2112a a <<≤或20.（Ⅰ）奇函数；(Ⅱ增函数；21.(Ⅰ)当01x ≤≤时()1f x x =+，当21x -≤≤-时1()f x x x=-- (Ⅱ) 12a ≥或 12a ≤- 22.（Ⅰ）224()log (1)(2)f x t =--+(Ⅱ)减函数（Ⅲ）29log 5 §3．1．1A 组1．C ；2．B ；3．B ；4．D ；5．D ；6．C ；7．（Ⅰ）有＜（Ⅱ）有＜（Ⅲ）有＜; 8． 12-,13-;9． 0)()(≤⋅b f a f10． 223y x x =+-或2812y x x =-+.11．11,3⎡⎤--⎢⎥⎣⎦.12． 1个 B 组1．B ；2．B ； 3．20; 4． (],1-∞ C 组1．A ；2．C ；3．4; 4．（Ⅰ）()f x 在()1,-+∞上为增函数;（Ⅱ）函数()f x 没有负值零点.§3．1．2A 组1．C ；2．C ；3．A ；4．D ；5．C ；6．B ；7． [2,2.5);8．[2,4];9．0,2;10．不能用二分法求函数的零点. 11．近似值为1.53.12．截去的小正方形的边长大约是1.7cm 或9.3cm . B 组1．C ；2．C ； 3．2.2;4．解：可证得函数在区间（2，3）上为增函数，由题设有f(2)≈-0.31＜0,f(3)≈0.43＞0,由于f(2)·f(3)＜0，故函数f(x)在区间（2，3）内有一个零点x 0，即x 0∈(2,3).下面用二分法求函数f(x)=lnx-x2在区间（2，3）内零点的近似值：取区间（2，3）的中点x 1=2.5，用计算器算得f(2.5)≈0.12＞0，由于f(2)·f(2.5)＜0,所以x 0∈(2,2.5);再取区间（2，2.5）的中点x 2=2.25，用计算器算得f(2.25)≈-0.08＜0,由于f(2.25)·f(2.5)＜0，所以x 0∈(2.25,2.5). 同理可得x 0∈(2.25,2.375)， x 0∈(2.312 5,2.375).(*)（1）由于|2.312 5-2.375|=0.062 5＜0.1，所以区间［2.312 5,2.375］上任意一个实数x 0′均可作为f(x)在区间（2，3）内且精确度为0.1的零点的近似值（比如，可取x 0′=2.35,2.342,2.375等）；（2）接（*），同理可得，x 0∈(2.343 75,2.375),x 0∈(2.343 75,2.359 375), x 0∈(2.343 75,2.351 562 5),x 0∈(2.343 75,2.347 656 25).由于区间(2.343 75,2.347 656 25)的两个端点精确到0.1的近似值都是2.3，所以函数f(x)在区间（2，3）内精确到0.1的零点的近似值为2.3. C 组1.B ；2．B ；3．-1.7.;4．解：设y=x 3-3，则y=x 3-3在（1，2）上是一条连续不断的曲线，∴y=x 3-3在（1，2）上必有一零点x 0.取（1，2）的中点x 1=1.5, f(1.5)=0.375＞0,∴x 0∈(1,1.5).再取（1，1.5）的中点x 2=1.25, f(1.25)=-1.046 875＜0,∴x 0∈(1.25,1.5).再取（1.25,1.5）的中点x 3=1.375, f(1.375)=-0.400 390 625＜0,∴x 0∈(1.375,1.5).这样反复计算下去，直到x 0∈(1.441 406 25,1.443 359 375).∵区间两个端点精确到0.01都是1.44，∴y=x 3-3的一个零点为1.44.即33精确到0.01的近似值为1.44.§3．1．3A 组1． B ；2．C ；3．C ；4．A ；5．A ；6．B ；7．22log 2x x x <<;8．1119;9．2500; 10． ⎩⎨⎧-==.30,45b a 11．对甲、乙两种商品的资金投入分别为0.75万元和2.25万元，利润为1.05万元.12．设x 表示月份，则212()0,(),xy f x px qx p y g x a b c ⎧==++≠⎪⎨==⋅+⎪⎩根据已知代入1,2,3月的产量，得1,42 1.2,93 1.3,p q r p q r p q r ++=⎧⎪++=⎨⎪++=⎩及231,1.2,1.3,ab c ab c ab c +=⎧⎪+=⎨⎪+=⎩确定函数表达式()20.050.350.7f x x x =-++，()0.80.5 1.4x g x =-⨯+，利用计算器或计算机将4x =代入上述函数计算，得()4 1.3f =，()4 1.35g =.所以选择()0.80.5 1.4x g x =-⨯+更合适.B 组1．B ；2．D ； 3．10;4.42C θ=︒， 2.3min t ≈. C 组1．A ；2． A ；3．()*4ay x x N =∈;4．（1）初始电流c U R ==3101006⨯=6×10-5=0.06(mA)；（2）时间常数t =()361001050105RC s -=⨯⨯⨯=；（3）根据公式（*），1563e -=，即150.5e-=.§3．1．4A 组1．C ；2．C ；3．C ；4．C ；5．D ；6．C ；7．122.5;8．()1f x x=;9．2ln 2, 1024; 10．（Ⅰ）5t =小时时蓄水池中蓄水量最少；（Ⅱ）每天有10小时供水紧张.11．（Ⅰ）略（Ⅱ）由图可知当1x =时，max 2y =.12．模型7log 1y x =+符合公司要求.B 组1．C ；2．B ； 3． 7种 ; 4． (Ⅰ) ()300,02002300,200300t t f t t t -≤≤⎧=⎨-≤≤⎩； ()()()211501000300200g t t t =-+≤≤(Ⅱ) 当50t =时，西红柿收益最大.C 组1.B ；2．D ；31;4．（Ⅰ）函数关系式为()0.67778.2067f x x =+.（Ⅱ）()10.67778.20678.8844f =+=，()20.677728.20679.5621f =⨯+= 与表中相应的函数值相比，误差不超过0.1（万亿元）.（Ⅲ）预测2003年国内生产总值约为10.9175万亿元.基础训练A 组1．B ；2．A ；3．C ；4．D ；5．D;6．D ;7．C; 8．D;9．B; 10．C; 11．34a ≥-;12．2;13．π+44;14．()8000800012 0,63y a x a x x ⎛⎫=++∈+∞ ⎪⎝⎭15．（Ⅰ）()f x 是定义域R 上的奇函数且为增函数;（Ⅱ）略16． (Ⅰ)略; (Ⅱ)3=a 时,0123=+-+x x x,由025)1(,0)0(>=<f f 所以区间()0,1上必有一根, 由由单调性可知, 0123=+-+x x x至多有一根,故方程恰有一根在区间()0,1上. (Ⅲ)由二分法0)163(,0)165(,0)83(,0)41(,0)21(>>><>f f f f f ,7()0,32f <1325()0,()064128f f <>而1281641312825-=-,而01.01281<28.012825==∴ x 17． (Ⅰ)()22f x x x =-+；(Ⅱ)2,0m n =-=.综合训练1．B ；2．B ；3．A ；4．A ；5．B ；6．D ；7．A ;8．A ;9．B ; 10．D ;11．C ;12．A ;13．1.6；14．2；15．8；16．⑴⑶17．不等式的解集为{|2x x <18．（Ⅰ）当1a >时，()f x 的定义域为{|0}x x <；当01a <<时，()f x 的定义域为{|0}x x >. （Ⅱ）当1a >时，()f x 在(),0-∞上递减. 19．略20．（Ⅰ）()()614-∞⋃+∞，，;（Ⅱ）(),5-∞; （Ⅲ）(),2-∞; （Ⅳ）36142m m <≤≥或. 21．(Ⅰ)设函数()31x f x x a-=+的图象上有且仅有两个相异的稳定点，则31x x x a -=+，即⎩⎨⎧-≠=+-+a x x a x ,01)3(2有两个相异的根，所以⎪⎩⎪⎨⎧≠+--+->--.01))(3()(,04)3(22a a a a 解之，得5a >或1a <且13a ≠-.因此存在()11,,15,33a ⎛⎫⎛⎫∈-∞-⋃-⋃+∞ ⎪ ⎪⎝⎭⎝⎭使得函数()31x f x x a -=+的图象上有且仅有两个相异的稳定点.(Ⅱ)证明:因为函数()f x 是定义在R 上的奇函数，所以()00f =，因此()0,0是()f x 的一个稳定点.假设函数还有稳定点()00,x x ，即()00f x x =，则必定有()00f x x -=-.()00,x x --也是函数的稳定点.综上所述，奇函数的稳定点除原点外，都是成对出现，因此其稳定点的个数是奇数.22．（Ⅰ）当11,22x ⎡⎤∈-⎢⎥⎣⎦时，由定义知：x 与0距离最近，()f x x =，11,22x ⎡⎤∈-⎢⎥⎣⎦，当()11,22x k k k Z ⎡⎤∈-+∈⎢⎥⎣⎦时，由定义知：k 为与x 最近的一个整数，故()f x x k =-，()11,22x k k k Z ⎡⎤∈-+∈⎢⎥⎣⎦（Ⅱ）对任何x R ∈，函数()f x 都存在，且存在k Z ∈，满足1122k x k -≤≤+，()f x x k =-.由1122k x k -≤≤+可以得出1122k x k --≤-≤-+,由（1）的结论，()()f x f x -=,即()f x 是偶函数.。