王向东数学实验课本3-13
新编教科版小学四年级数学上册实验目录
新编教科版小学四年级数学上册实验目录实验一：数的认识与数形结合1. 实验名称：认识数- 实验目的：通过实物与数字的对应来认识数的概念。
- 实验材料：实物物品（如书本、笔、橡皮等）、数字卡片。
- 实验步骤：1. 老师出示一组实物，让学生用数字卡片表示实物的数量。
2. 学生按照实物数量使用数字卡片进行配对。
3. 学生自由组合实物和数字卡片进行数的认识练。
2. 实验名称：掌握数的顺序- 实验目的：通过游戏形式帮助学生掌握数的顺序。
- 实验材料：数字卡片、计数表。
- 实验步骤：1. 老师发放数字卡片，并要求学生根据卡片上的数依次排队。
2. 学生按照数字大小进行排序，并用计数表记录下来。
3. 学生与同伴进行比较，看谁能排队得最快。
3. 实验名称：数形结合- 实验目的：通过实物与数字的对应，帮助学生将抽象的数字与具体的物品联系起来。
- 实验材料：实物物品、数字卡片。
- 实验步骤：1. 老师出示一组实物物品，并让学生根据实物数量选择相应的数字卡片。
2. 学生将实物与对应的数字卡片进行配对。
3. 学生通过数形结合的游戏，加深对数字与实物的联系。
实验二：加法与减法初步认识1. 实验名称：认识加法- 实验目的：通过实际操作帮助学生认识加法的概念。
- 实验材料：实物物品、数字卡片。
- 实验步骤：1. 老师出示一组实物物品，并告诉学生两组实物的数量。
2. 学生使用数字卡片表示实物的数量，并将两组实物的数量相加得出总数。
3. 学生通过实际操作认识加法的意义。
2. 实验名称：认识减法- 实验目的：通过实际操作帮助学生认识减法的概念。
- 实验材料：实物物品、数字卡片。
- 实验步骤：1. 老师出示一组实物物品，并告诉学生初始数量和被减数量。
2. 学生使用数字卡片表示实物的数量，并将被减数量从初始数量中减去得出剩余数量。
3. 学生通过实际操作认识减法的意义。
3. 实验名称：加减法运算练- 实验目的：通过加减法运算练巩固学生对加法和减法的理解。
第2课时 (王之东)3.1.1一元一次方程1.2(10、27)
3
（C）12
（D）－12
三、应用概念 巩固延伸
练习2：请每位同学写出一个简单的一元一
次方程，同桌同学互相估算对方方程的解，
再请出题者检验是否正确．
三、应用概念 巩固延伸
练习3：某班开展为贫困山区学校捐书活动，捐的书 比平均每人捐3本多21本，比平均每人捐4本少27本 ，求这个班有多少名学生？如果设这个班有x名 学生，请列出关于x的方程并估算方程的解.
3列方程的一般步骤 ①设(用字母表示未知数) ②找(能表示问题全部含义的相等关系) ③列(方程)
。
4一元一次方程的特征是什么？
①都只含有一个未知数；
②未知数的次数都是1；
③等号两边都是整式； ④都是方程。
一元一次方程： 只含有一个未知数(元),未知 数的次数都是1，等号两边都是整式，这样 的方程叫一元一次方程。
二、尝试归纳 探究新知
任取x的值
代入
1 700+150x=2 450
不成立
成立
得方程的解
解方程就是求出使方程中等号左右两 边相等的未知数的值的过程，这个值就是 方程的解．
思考1
想一想:⑴使得方程4x=24成立的x的值为 多少？ 当x=6时，方程4x=24成立。 (2)使得方程5x+2=12成立的x的值为多少？
设这个足球场的宽为x米，则长 为(x+36)米，可列出方程
2x ( x 36) 344 。
如果设射击队获 得的金牌数为x
6=2x-2
练一练(根据下列问题中的条件列出方程)
国庆期间，“天一广场”搞促销 活动，小颖的姐姐买了一件衣 服，按8折销售的售价为72元， 问这件衣服的原价是多少元？x 72
年销售额的回归模型预测
学号武汉理工大学数学建模与仿真课程设计设计题目专业班级姓名指导老师2011年 1 月16 日附件2：课程设计任务书学生姓名：专业班级：指导教师：工作单位：题目:初始条件：要求完成的主要任务:（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）时间安排：指导教师签名：年月日系主任（或责任教师）签名：年月日年销售额的回归模型预测【摘要】本文首先利用题目所给数据做出散点图，分析自变量与因变量之间的线性关系，建立基本的线性回归模型t t t x y εββ++=10[1]，对所建立的模型直接用MATLAB 统计工具箱[2]求解，得到的回归系数估计值及其置信区间（置信水平05.0=α）、检验统计量2R ,F ,P [3]，将参数估计值代入初始模型得到t t x y 17628.04548.1+-=∧。
但是这个模型没有考虑到题目所给的数据是一个时间序列。
实际上，在对时间序列数据作回归分析时，模型的随机误差项t ε有可能存在相关性。
违背模型关于t ε（对t ）相互独立的基本假设。
所以对原模型进行自相关检验，发现其随机误差存在正自相关，故对原模型作变量变换：1'--=t t t y y y ρ ，1'--=t t t x x x ρ得到新的模型：t t t u x y ++=''1'0'ββ，其中，()ρββ-=10'0，1'1ββ=。
对新的模型利用MATLAB 统计工具箱求解，并对新的模型也作一次自相关检验，即诊断随机误差t u 是否还存在自相关，经检验认为新的模型中随机误差不存在自相关。
因此经变换所得到的回归模型t t t u x y ++=''1'0'ββ是适用的。
最后，将模型t t t u x y ++=''1'0'ββ中的't y 和't x 还原为原始变量t y 和t x ，得到结果为：111099.01737.06326.03916.0--∧-++-=t t t t x x y y关键词：时间序列 回归模型 统计检验 D —W 检验一、问题重述与分析1.1、问题提出某公司（记为A）想用全行业的销售额作为自变量来预测公司的销售额,表1给出了2006年～2010年公司销售额和行业销售额的分季度数据(单位:百万元)。
数学建模 养鱼问题的最优模型
养鱼问题的最优模型摘 要：本文是根据鱼本身的生长情况，求利润最大化的养鱼规划及解决养鱼问题的数学模型，并利用相关分析解决我们的养鱼问题。
利用线性回归、微分方程分析研究鱼苗的产值，来获取最佳综合效益。
关键词：养鱼模型 线性规划 最大利润 微分方程一、问题重述在某地有一个池塘，其水面面积约为100×1002m ，用来养殖某种鱼类。
在如下的假设下，设计能获取较大利润的三年的养鱼方案。
①鱼的存活空间为1kg /2m ；②每1kg 鱼每天需要的饲料为0.05kg ，市场上鱼饲料的价格为0.2元/kg ；③鱼苗的价格忽略不计，每1kg 鱼苗大约有500条鱼；④鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；⑤池内鱼的繁殖与死亡均忽略；⑥若q 为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kgQ 元元元元⑦该池内只能投放鱼苗。
二、问题分析要设计获得最大利润的养鱼方案，首先不考虑鱼的制约条件，如环境，由各种竞争导致的灭亡。
由鱼塘的面积、鱼的存活空间，每1kg 鱼每天需要的饲料，以及鱼饲料的价格，分析鱼的价值取向来考虑和设计一个最佳的养鱼方案。
但是由于养鱼的复杂性，忽略部分影响养鱼的因素，并应用线性规划模型解决养鱼问题。
三、 模型假设1、鱼塘只有鱼苗；2、不考虑鱼的繁殖以及由生存环境、不受时间、季节的限制来构成的死亡因素；3、鱼苗成鱼的过程服从生长系数。
4、放入的鱼苗不受个体差异的影响，都能按照题目所给的条件生长，同时放入的 鱼苗在相同的时间内都能长到同样大。
5、鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；四、符号说明以下为本文中使用的符号：1 0q 最初放入的鱼的数量2 k 鱼每天增重的比例3 t 时间（第t 天）4 )(t q 每条鱼在t 天下的重量5 )(t C 每条鱼在养殖t 天的条件下需要的饲料费用6 M 三年的收益总额五、模型求解根据池塘的容量，由鱼苗长成成鱼时的质量为2kg ，每条鱼的存活空间为1kg/m 2,则最初放入的鱼的数量为0q ，可由已知条件得到以下微分方程：kq dtt dq )( （1）kte q t q 0)(= （2） 50010=q （3） 2)365(=q （4） 通过计算可以得出： 01983.0=k故 ：养殖t 天的条件下每条鱼的重量为)(t q ，则01983.05001)(e t q = （5）根据已知条件计算出：;2)365(;5.1)334(;75.0)313(;2.0)243(====q q q q每天每公斤鱼的成本：.01.02.005.0元=⨯鱼的重量和养殖时间的关系表我们知道，01983.0=k ，养殖t 天的条件下每条鱼的重量为)(t q ：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kgQ 元元元元设养殖t 天的条件下每条鱼需要的饲料费用为)(t C∑∑==+=⨯⨯+=ti i ti ik k t C 11)1(5000/12.005.0)1(500/1)( （6）三种鱼的情况分析：计算可得：每条鱼的平均利润为24.506667元。
王向东数学实验课本(可编辑)2-1
实验一 曲线绘图【实验目的】1．了解曲线的几种表示方法。
2．学习掌握MATLAB 软件有关的命令。
【实验内容】绘制下列三种曲线：1． 以直角坐标方程x y x y cos ,sin ==表示的正、余弦线。
2． 以参数方程]2,0[,sin ,cos π∈==t t y t x 表示的平面曲线（单位圆）。
3． 以参数方程]20,0[,,sin 2,2cos 2.02.0∈===--t t z t e y t ex t tππ表示的空间曲线。
4． 以极坐标方程]2,0[,1),cos 1(πϕϕ∈=+=a a r 表示的心脏线。
【实验准备】1．平面、空间曲线的表示形式对于平面曲线，常见的有三种表示形式，即以直角坐标方程],[),(b a x x f y ∈=，以参数方程],[),(),(b a t t y y t x x ∈==，和以极坐标],[),(b a r r ∈=ϕϕ表示等三种形式。
而对于空间曲线，常见的是用参数方程],[),(),(),(b a t t z z t y y t x x ∈===表示。
2．曲线绘图的MATLAB 命令MATLAB 中主要用plot,fplot,plot3三种命令绘制不同的曲线。
可以用help plot, help fplot, help plot3查阅有关这些命令的详细信息【实验方法与步骤】练习1 作出函数x y x y cos ,sin ==的图形，并观测它们的周期性。
先作函数x y sin =在]4,4[ππ-上的图形，用MA TLAB 作图的程序代码为：>>x=linspace(-4*pi,4*pi,300); %产生300维向量x>>y=sin(x);>>plot(x,y) %二维图形绘图命令结果如图1.1，上述语句中%后面如“%产生300维向量x ”是说明性语句，无需键入。
图1.1 的图形此图也可用fplot 命令，相应的MATLAB 程序代码为： >>clear; close; %clear 清理内存；close 关闭已有窗口。
高等教育出版社样书目录（数学类）
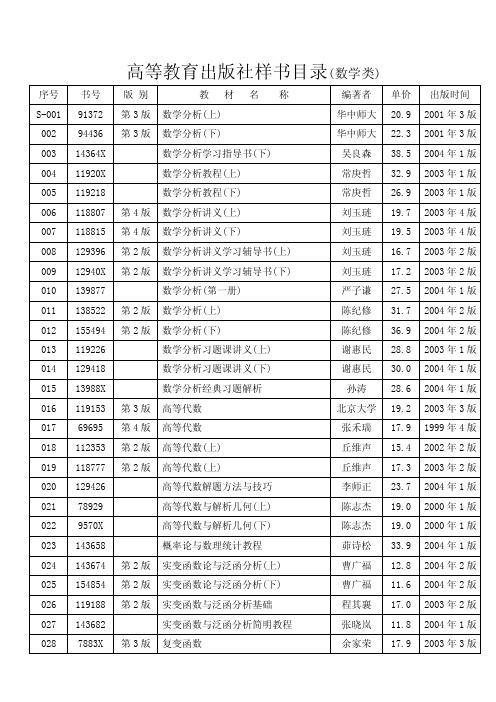
同济大学 10.1 2001 年 2 版
重温微积分
齐民生 39.6 2004 年 1 版
第 2 版 微积分(上)
同济大学 24.9 2003 年 2 版
第 2 版 微积分(下)
同济大学 23.1 2003 年 2 版
微积分学习辅导与习题选解
同济大学 28.4 2004 年 1 版
第 2 版 微积分学简明教程(上)
余家荣 17.9
出版时间 2001 年 3 版 2001 年 3 版 2004 年 1 版 2003 年 1 版 2003 年 1 版 2003 年 4 版 2003 年 4 版 2003 年 2 版 2003 年 2 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 1 版 2004 年 1 版 2004 年 1 版 2003 年 3 版 1999 年 4 版 2002 年 2 版 2003 年 2 版 2004 年 1 版 2000 年 1 版 2000 年 1 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 2 版 2004 年 1 版 2003 年 3 版
高等教育出版社样书目录(数学类)
版别
教材名 称
编著者 单价 出版时间
第4版 第3版
概率论与数理统计教程 概率论与数理统计教程学习辅导与习题 选解
概率论与数理统计
沈恒范 沈恒范 盛骤
20.6 2003 年 4 版 17.6 2003 年 1 版 19.3 2001 年 3 版
概率论与数理统计习题全解指南
第 2 版 数学史概论
李文林 21.0 2002 年 2 版
大学文科高等数学(第一册)
姚孟臣 11.9 1997 年 1 版
蜂窝纸板的动态缓冲特性的研究
摘要蜂窝纸板是根据自然界蜂巢结构原理制作的，蜂窝纸板以纸作为原材料，绿色环保，来源广泛，对环境的影响较小，是替代发泡塑料的的新型材料。
蜂窝纸板在运输过程中，搬运、装卸、堆码、销售环节产生的冲击和振动等力学因素会对蜂窝纸板的力学性能造成一定的影响，从而提高内装物破损的几率本课题以蜂窝纸板为研究对象，利用改变蜂窝纸板的厚度、实验中重锤的跌落高度使用跌落试验仪，得到蜂窝纸板的动态缓冲曲线最大加速度-静应力曲线（Gm-δm）和最大加速度厚度曲线（Gm-h），并根据所得的曲线得出蜂窝纸板厚度、最大加速度和应力之间的关系，结论是：蜂窝纸板受冲击的最大加速度和静应力、冲击初速度有密切关系，随着静应力的增加，峰值加速度减小，冲击初速度增加，峰值加速度减小，蜂窝纸板的缓冲性能较好。
关键词：蜂窝纸板，动态缓冲特性，跌落高度，压溃ABSTRACTMade of honeycomb honeycomb structure is based on the natural world, honeycomb paper as raw materials, green environmental protection, sources, less impact on the environment, is to replace the plastic foam material. Cellular cardboard in transport process in the, handling, and handling, and heap code, and sales link produced of impact and vibration, mechanical factors will on cellular cardboard of mechanical performance caused must of effect, to improve within loaded real damaged of chances this subject to cellular cardboard for research object, using change cellular cardboard of thickness, and experiment in the heavy hammer of fell height using fell test instrument, get cellular cardboard of dynamic buffer curve maximum acceleration-static stress curve (Gm-δ m) and maximum acceleration thickness curve (Gm-h), And according to the curve drawn honeycomb thickness, maximum acceleration and the relationship between stress, the conclusion is: hit the maximum acceleration of honeycomb paperboard and static stresses, impact velocity is closely related, with the increase of stress, peak acceleration is reduced, increased impact velocity, peak acceleration is reduced, good cushioning properties of honeycomb paperboard.KEY WARDS:Honeycomb cardboard, dynamic cushioning properties, drop height, crushing目录第1章绪论 (1)1.1运输包装 (1)1.1.1运输包装的要求 (4)1.1.2运输包装的形式 (4)1.2蜂窝纸板在运输包装上的应用 (6)1.3国内外蜂窝纸板的研究现状 (7)1.3.1国内蜂窝纸板的研究现状 (7)1.3.2国外蜂窝纸板的研究现状 (7)1.4本课题研究目标 (8)第2章蜂窝纸板综述 (10)2.1蜂窝纸板的定义 (10)2.2蜂窝纸板的结构 (10)2.3蜂窝纸板的发展 (11)2.3.1蜂窝纸板的由来 (11)2.3.2我国蜂窝纸板的起步 (12)2.3.3蜂窝纸板的发展 (12)2.4蜂窝纸板的技术要求 (13)2.4.1材料和尺寸 (13)2.4.2蜂窝纸板的平压强度和静态弯曲强度 (15)2.4.3其他技术要求 (16)2.5蜂窝纸板的制作工艺与应用 (17)2.5.1蜂窝纸板的制作工艺 (17)2.5.2蜂窝纸板的应用 (18)第3章实验设计 (20)3.1实验目的 (20)3.2实验原理 (20)3.3实验仪器 (23)3.3.1实验仪器介绍 (23)3.3.2系统功能 (24)3.3.3系统构成 (24)3.3.4实验仪器特点 (25)3.4实验内容 (26)3.4.1准备阶段 (26)3.4.2实验步骤 (27)第4章实验结果及数据分析 (29)4.1实验结果 (29)4.2数据分析 (31)第5章总结 (36)参考文献 (37)致谢 (39)诚信声明第1章绪论1.1运输包装运输包装，是为了降低在运输流通的过程中各种外界因素对产品造成的损坏，以保障被包装产品的安全，也为了方便储运与装卸，加速交接点验节省劳动必要时间，人们将包装中以运输储运为主要目的的包装成为运输包装，又被称为外包装，其主要作用在于保护商品免受或减轻外部因素所造成的伤害，防止在储运过程中发生货物的损坏，并最大限度地避免在运输过程中各种外界条件对商品可能产生的影响，方便产品的检验、计数和分拨。
数学实验实验报告三答案
实验三实验内容：1、对于离散数值给出的函数，编制用辛普森公式计算定积分的程序，命名为simp.m;新建M文件，源程序：function s=simp(y,h,m)s=0;for k=1:ms=s+4*y(2*k);endfor k=1:(m-1)s=s+2*y(2*k+1);ends=(s+y(1)+y(2*m+1))*h/3;2、教材97页第1题；用矩形、梯形和辛普森三种公式计算由下表数据给出的积分x所产生，将计算值与精确值作比较。
已知该表数据为函数y=x+sin3源程序：y=[0.3895 0.6598 0.9147 1.1611 1.3971 1.6212 1.8325];s1=sum(y(1:6))*0.2 %矩形s2=trapz(y)*0.2 %梯形s3=simp(y,0.2,3) %辛普森s4=(0.5*1.5*1.5-3*cos(1.5/3))-(0.5*0.3*0.3-3*cos(0.3/3))%精确值 s1 = 1.2287s2 =1.3730s3 =1.3743s4 =1.4323经观察可发现由辛普森公式计算得到的结果与精确值最相近。
3、 教材97页第2题；（选一个函数即可）选择一些函数用梯形、辛普森和随机模拟三种方法计算积分。
改变步长（对梯形公式），该表精度要求（对辛普森公式），改变随机点数（对随机模拟），进行比较、分析。
选择函数y=11 x ，0≦x ≦1。
新建M 文件，程序：function y=fun3_2a(x)y=1./(x+1);源程序：h=1/200;x=0:h:1;y=fun3_2a(x);z1=trapz(y)*h %梯形公式z2=quad('fun3_2a',0,1,1e-7) %辛普森公式n=10000;x=rand(1,n); %随机模拟方法y=fun3_2a(x);z3=sum(y)/nz4=log(2) %利用原函数计算的积分准确值z1 =0.6931z2 =0.69314、教材98页第7题。
数学 暑期绘本版教案 二升三-13 动手移一移
第13讲百变大咖秀——动手移一移【教学内容】《数学思维训练教程》暑期绘本版，2升3第13讲“百变大咖秀——动手移一移”。
【教学目标】知识技能利用火柴棒摆出数字或图形，锻炼学生们的动手操作能力、形象思维能力和创造力等。
数学思考通过实际问题的解决，体会摆火柴棒游戏中蕴含的数学知识。
问题解决在灵活多变的游戏活动中，品尝到游戏的无穷乐趣。
情感态度通过用火柴棒摆出图形和巧移火柴棒等活动,培养学生动手能力,丰富想象能力。
培养学生创造思维能力。
【教学重点和难点】教学重点采用“移动”或“去掉”火柴棒的方法进行游戏。
教学难点在摆火柴棒游戏中能探索不同的方法。
【教学准备】动画多媒体语言课件、火柴棒若干根。
第一课时教学过程：教学路径学生活动方案说明一、课前谈话，增强互信：暑假里，欢欢、乐乐、多多还有很多佳一的小伙伴一起参加百变大咖秀节目。
今天的百变大咖秀可不同以往，因为里面有很多有趣的数学问题呢。
揭示课题：动手移一移二、自主探究教学例1百变大咖秀第一场：阳台左边放了3盆红花，右边放了3盆黄花，怎么移，可以使红花、黄花间隔排列。
例1：阳台左边放了3盆红花，右边放了3盆黄花，多多想通过移动，把红花和黄花交换位置，最少交换几次就可以使红花和黄花间隔排列？题干中6盆花都可以任意移动。
小朋友，你知道多多是怎样想的吗？仔细观察图形，启发学生思考，怎样移就可以使红花和黄花间隔排列？同桌讨论。
师：还有其他的方法吗？学生思考，尝试移一移。
师：但是题目要求要交换的次数最少，最少的情况是怎么交换呢？提示：红花和黄花间隔排列就是把红花和黄花一个隔一个地排一行。
（依次间隔地出示红、黄花盆）下一步：“最少”交换就是两种花互换的次数最少。
答案：动画演示交换第2盆和第5盆花。
答：最少交换1次就可以使红花和黄花间隔排列。
教学例2百变大咖秀第二场：乐乐拿出了6枚硬币，他要干什么用呢？例2：（旁白女）乐乐用6枚硬币在桌面上摆成了一个三角形，如图：请你移动两枚硬币，使这个三角形颠倒过来。
王向东数学实验课后习题解答(第二篇2.1-2.10)
数学实验课后习题解答配套教材：王向东戎海武文翰编著数学实验王汝军编写实验一曲线绘图【练习与思考】画出下列常见曲线的图形。
以直角坐标方程表示的曲线：1.立方曲线3x y=clear;x=-2:0.1:2; y=x.^3; plot(x,y)2.立方抛物线3x y=clear;y=-2:0.1:2; x=y.^3; plot(x,y) grid on3.高斯曲线2xe y-=clear;x=-3:0.1:3;y=exp(-x.^2); plot(x,y); grid on%axis equal以参数方程表示的曲线4. 奈尔抛物线)(,3223x y t y t x ===clear;t=-3:0.05:3; x=t.^3;y=t.^2; plot(x,y) axis equal grid on5. 半立方抛物线2323,()x t y t y x ===clear;t=-3:0.05:3; x=t.^2;y=t.^3; plot(x,y) %axis equal grid on6.迪卡尔曲线2332233,(30)11at at x y x y axy t t==+-=++ clear;a=3;t=-6:0.1:6; x=3*a*t./(1+t.^2); y=3*a*t.^2./(1+t.^2); plot(x,y)7.蔓叶线233222,()11at at x x y y t t a x===++- clear;a=3;t=-6:0.1:6;x=3*a*t.^2./(1+t.^2); y=3*a*t.^3./(1+t.^2); plot(x,y)8. 摆线)cos 1(),sin (t b y t t a x -=-=clear;clc; a=1;b=1;t=0:pi/50:6*pi; x=a*(t-sin(t)); y=b*(1-cos(t)); plot(x,y); axis equal grid on9. 内摆线（星形线）)(sin ,cos 32323233a y x t a y t a x =+==clear;a=1;t=0:pi/50:2*pi; x=a*cos(t).^3; y=a*sin(t).^3; plot(x,y)10. 圆的渐伸线（渐开线）)cos (sin ),sin (cos t t t a y t t t a x -=+=clear; a=1;t=0:pi/50:6*pi;x=a*(cos(t)+t.*sin(t)); y=a*(sin(t)+t.*cos(t)); plot(x,y) grid on11. 空间螺线ct z t b y t a x ===,sin ,coscleara=3;b=2;c=1; t=0:pi/50:6*pi; x=a*cos(t); y=b*sin(t); z=c*t;plot3(x,y,z) grid on以极坐标方程表示的曲线：12. 阿基米德线0,≥=r a rϕclear; a=1;phy=0:pi/50:6*pi; rho=a*phy;polar(phy,rho,'r-*')13. 对数螺线ϕa e r =clear; a=0.1;phy=0:pi/50:6*pi; rho=exp(a*phy); polar(phy,rho) 14. 双纽线))()((2cos 22222222y x a y x a r -=+=ϕclear; a=1;phy=-pi/4:pi/50:pi/4; rho=a*sqrt(cos(2*phy)); polar(phy,rho)hold onpolar(phy,-rho)15. 双纽线)2)((2sin 222222xy a y x a r =+=ϕclear; a=1;phy=0:pi/50:pi/2;rho=a*sqrt(sin(2*phy)); polar(phy,rho) hold onpolar(phy,-rho)16. 四叶玫瑰线0,2sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(2*phy); polar(phy,rho)17. 三叶玫瑰线0,3sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(3*phy); polar(phy,rho)18. 三叶玫瑰线0,3cos ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*cos(3*phy); polar(phy,rho)实验二 极限与导数【练习与思考】1． 求下列各极限（1）nn n)11(lim -∞→ （2）n nn n 3lim 3+∞→ （3）)122(lim n n n n ++-+∞→clear;syms ny1=limit((1-1/n)^n,n,inf)y2=limit((n^3+3^n)^(1/n),n,inf)y3=limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf)y1 =1/exp(1) y2 =3 y3 =0（4）)1112(lim 21---→x x x （5）x x x 2cot lim 0→ （6）)3(lim 2x x x x -+∞→clear; syms x ;y4=limit(2/(x^2-1)-1/(x-1),x,1) y5=limit(x*cot(2*x),x,0)y6=limit(sqrt(x^2+3*x)-x,x,inf)y4 =-1/2 y5 =1/2 y6 =3/2（7）x x x m )(cos lim ∞→ （8）)111(lim 1--→x x e x （9）x x x 11lim30-+→ clear;syms x my7=limit(cos(m/x),x,inf)y8=limit(1/x-1/(exp(x)-1),x,1) y9=limit(((1+x)^(1/3)-1)/x,x,0)y7 =1y8 =(exp(1) - 2)/(exp(1) - 1) y9 =1/32． 考虑函数22),sin(3)(32<<-=x x x x f作出图形，并说出大致单调区间；使用diff 求)('x f ，并求)(x f 确切的单调区间。
投针实验计算圆周率的数学分析
投针实验计算圆周率的数学分析王向东投针实验计算圆周率的数学证明方法，初中一般是采取假设针弯成直径等于平行线距离的方法巧妙证明。
这个方法是基于不管针弯成什么形状，针上的每一个部位与平行线相交的概率相同，但这是感观上的认识，要把其中原因解释清楚不是很容易。
笔者从纯数学的角度来推导这个公式。
一、投针问题的由来1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的蒲丰投针问题。
这一方法的步骤是：1) 取一张白纸，在上面画上许多条间距为d 的平行线。
2) 取一根长度为()l l d <的针，随机地向画有平行直线的纸上掷n 次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为d 的平行线，将一根长度为()l l d <的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。
”布丰本人证明了，这个概率是：2lp d π=，π为圆周率。
二、投针实验的数学证明投针这个动作是由两个事件构成的。
事件1：针投下后与平行线构成一定的夹角。
我们来分析一下针投下后与平行线之间的成某一特定夹角时的概率。
设针投下后与平行线之间的夹角为θ，则θ在0与π之间。
针与平行线之间的夹角在θ到θ+θ∆之间的概率为1p θπ∆=，当0θ∆→时，可看作针投下后与平行线之间成某一特定夹角为θ的概率。
事件2：针投下后会在平行线垂直的方向形成一个投影，针与平行线相交等于它的垂直投影与平行线相交。
这个投影的长度'l 在0到l 之间。
此时针在水平方向的投影为'sin()l l θ=。
再分析'l 与平行线相交的概率。
等于我们将问题转化成长度为'l 的针，并且只允许它处在与平行线垂直的方向上，这时它与平行线相交的概率显然为：2'sin()l l p d d θ==因为每一次投掷都是由上述两个事件组成的，因而对于针与平行线之间的夹角在θ到θ+θ∆之间时，针与平行线相交的概率()p θ为这两个事件概率的乘积，即：12sin()().l p p p d θθθπ∆== 因为针与平行线之间构成的夹角在0－π之间每个角度的机会都是均等的，因此针与平行线相交的概率相当于针落在每个θ附近θ∆范围内，当0θ∆→时与平行线相交的所有概率之和。
【精品】运输问题优化模型
运输问题优化模型运输方案问题的优化模型摘要：本文研究运输最优化问题。
运输问题(Transportation Problem)是一个典型的线性规划问题。
一般的运输问题就是要解决把某种产品从若干个产地调运到若干个销地，在每个产地的供应量与每个销地的需求量已知，并知道各地之间的运输单价的前提下，如何确定一个使得总的运输费用最小的方案的问题。
本论文运用线性规划的数学模型来解决此运输问题中总费用最小的问题。
引入x变量作为决策变量，建立目标函数，列出约束条件，借助LINGO软件进行模型求解运算，得出其中的最优解，使得把某种产品从2个产地调运到3个客户的总费用最小。
关键词：LINGO软件运输模型最优化线性规划1问题重述与问题分析1、1 问题重述要把一种产品从产地运到客户处,发量、收量及产地到客户的运输费单价如表1所示。
表1 运输费用表客户1 客户2 客户3 发量产地1 10 4 12 3000 产地2 8 10 3 4000 需求量2000 1500 5000这是一个供求不平衡问题，产品缺少1500个单位，因此决定运输方案应按下列目标满足要求：第一目标，客户1为重要部门，需求量必须全部满足；第二目标，满足其他两个客户至少75%的需要量；第三目标，使运费尽量少；第四目标，从产地2到客户1的运量至少有1000个单位。
1、2 问题分析运输方案就是安排从两个产地向三个客户运送产品的最佳方案，目标是使运费最少。
而从题目来看产品的总量只有7000个单位，客户的需求量却有8500个单位，产品明显的缺了1500各单位，所以至少要按以下要求分配运输，首先客户1为重要部门，需求量必须全部满足，从产地2到客户1的运量至少有1000个单位，即至少向客户1发2000个单位，且从产地2向客户1发的要大于等于1000个单位；其次满足其他两个客户至少75%的需要量，即至少得向客户2发1125个单位，至少向客户3发3750个单位。
最佳的运输方案就是满足了要求中的发量，而让运输费用最少的方案。
冀教版2024新版七年级数学上册1.3 绝对值与相反数 教案
1.3绝对值与相反数教学目标1.能借助数轴理解相反数和绝对值的意义，会求一个数的相反数和绝对值.在实际生活中能知道相反数和绝对值的意义.会用字母表示一个数的绝对值和这个数的关系，并能借此解决一些简单的问题.2.经历将实际问题数学化的过程，感受数学在生活中的应用价值，经历用字母表示规律的过程，感受由特殊到一般的特点.教学重难点【教学重点】理解绝对值、相反数的意义，会求一个数的相反数和绝对值.【教学难点】会用绝对值、相反数的意义解释一些实际问题和现象。
教学过程一、新课导入观察下图中图形的位置，试着描述它们之间的距离。
向左边移动_____格，与的距离是____格，向右边移动____格，与的距离是____格，它们之间的距离是_____格师生活动：教师展示动画，引导学生思考，如何计算物体间的距离，并与学生一起完成填空．答：3，3，2，2，5设计意图：让学生体会现实生活中的数学，从动画中感受距离及其变化，从而引出新课。
二、新课讲解1.绝对值的定义一起探究问题1：甲、乙两辆从同一处O出发，分别向东、西方向行驶10km，到达A、B两处.它们的行驶路线相同吗？行驶路程相等吗？记向东行驶的里程数为正.两辆出租车都从O地出发，甲车向东行驶10km到达A处，记作__km，乙车向西行驶10km到达B处，记作____km.预设答案：+10，-10以O为原点，取适当的单位长度画数轴，并在数轴上标出A、B的位置，则点A与原点距离是__，点B与原点距离是___.预设答案：10，10师生活动：教师提出问题并展示动画，展示动画前，教师可以让学生自己动手画画，并思考回答问题1，之后，教师可以按照上面的思路引导学生进行规范性的探究，一步步的引出我们所需要的答案，最终归纳得出绝对值的定义.定义：在数轴上，表示一个数的点到原点的距离叫做这个数的绝对值，用“| |”表示.设计意图：通过实际问题把绝对值的定义明显地揭示出来，让学生体会从生活到数学知识形成的过程，在师生的对话中，学生已经不知不觉地直观感受到数轴上绝对值的定义.例题讲解例1 (1)用数轴上的点表示下列各组数：①3，-3；②5，-5；③33 ,-. 55(2)观察上述各组点在数轴上的位置，写出这些数的绝对值. 解：（1）如图所示.（2）观察各点在数轴上的位置，得到①|3|=3，|-3|=3；②|5|=5，|-5|=5；③3333 =,-=. 5555师生活动：由学生自主完成解答，教师展示给出解答示范．设计意图：巩固所学知识，加深对所学知识的理解，提高学生知识的综合运用能力．练一练：5的绝对值是( )A.5B.-5C. 15 D.15答案：A2.相反数的概念一起探究问题2：在数轴上，与原点距离是2的点有几个？这些点各表示哪个数？师生活动：学生画数轴自主探究，独立思考后，交流并发言，教师提出问题，并展示探究过程及结论.在数轴上，与原点距离是2的点有__2__个,分别表示_-2和2_____.设计意图：让学生学会寻找到原点距离相等的点个数的思想方法，为探究问题3做好准备. 问题3：设a是一个正数，数轴上与原点距离等于a的点有几个？这些点表示的数有什么关系？师生活动：学生按照问题2的思路进行探究，独立思考后，交流并发言，教师提出问题，并展示探究过程及结论.在数轴上，与原点距离是a的点有__2__个,分别表示_-a和a_____.设计意图：让学生体会从特殊到一般的数学思想，为引出相反数的概念打下基础.知识要点定义：符号不同、绝对值相等的两个数，我们称其中一个数是另一个数的相反数，这两个数互为相反数.a和-a互为相反数.0的相反数规定为0.归纳：互为相反数的两个数分别位于原点的两侧（0除外）；互为相反数的两个数到原点的距离相等.一般地，设a是一个正数，数轴上与原点的距离是a的点有两个，它们分别在原点的两侧，表示a和-a，这两点关于原点对称.师生活动：教师引导学生进行归纳，并及时提醒及纠正，最终得出相反数的概念.设计意图：得出相反数的概念，培养学生的逻辑思维和抽象概括能力。
种群增长模型
楚雄师范学院2013年首届“雁峰杯”数学建模竞赛论文题目种群增长规律模型2013 年5月26日种群增长规律模型摘要：某个自然环境中只有一种生物的群体（生态学上称种群）生存时，人们常用Logistic模型来描述这个种群数量的演变过程。
而且一个种群就不存在相互竞争、相互依存或是弱肉强食的关系。
本文在Logistic模型基础上，根据种群数量的统计数据，建立种群指数增长模型，并利用Matlab这一数学软件对所统计的数据进行拟合，最后对模型进行分析和评价。
关键词：Logistic模型生物种群指数增长 Matlab软件一、问题重述在某个地区生长着一个种群（一类生物群落），主要依靠自然资源存活并繁殖，假设该种群单位时间的增长量与其数量成正比。
一个动物学家在2012年对的数量。
假设该地区最多只能容纳该种群2000只，请计算出该种群达到最大容量的大概时间。
二、问题分析种群的数量随时间变化而变化，根据统计数据绘出曲线图如图1。
图表 1种群数量的动态变化由图表1所绘曲线图可知种群的数量变化趋势大致成指数曲线增长，类似于其他生物种群数量的动态变化趋势。
对于生物种群的这种指数曲线的动态变化趋势，往往用Logistic模型来描述，并且根据种群的统计数据利用Matlab软件处理。
利用所得的模型对以往种群的数量进行推算预测，可检验模型的精确度，以便对模型进行改进。
三、模型假设1、假设环境环境条件允许生物种群数量有一个最大值，即环境容纳量N，当种群数量达到环境最大容纳量时，种群数量不再增长；2、种群数量的增长简单利用固有增长率r来描述；3、种群中每个个体处于同一水平，在种群增长的过程中隔天到差异如年龄结构等个不予考虑；4、在所研究地区只考虑区域内部的种群数量，不考虑种群在区域间的迁入与迁出；5、种群总数是随时间连续变化的。
四.符号说明t :时间；x：种群在t时的数量；)(tr :种群的固有增长率；N ：种群的最大数量；五.模型的建立与求解根据模型的假设，在最大容量为2000只，种群生长不受其他任何条件的限制，也就是说食物等能充分满足种群需求的情况下，种群就能充分发挥其增长能力，数量迅速增加，呈现指数增长规律，也称为“J”型增长，这种增长变化的曲线如图表2所示图表 2种群数量散点图种群在有限环境中的增长不是“J ”型，而是“S ”型，但因为在较大的空间容量，以及不考虑其它因素的情况下，种群在有限环境中的增长也可以看做是“J ”型增长，即符合“S ”型增长曲线的logistic 模型是同等的。
数学建模教材目录
数学建模教材目录(2008年10月整理）1982年以来国内正式出版的数学建模教材、译著及竞赛辅导材料，及与数学建模相关的数学实验教材（仅据各地告知的统计）：1.E.A.Bender.数学模型引论.朱尧辰、徐伟宣译，科学普及出版社，1982.2.近藤次郎.数学模型.宫荣章等译，机械工业出版社，1985.3.C.L.戴姆、E.S.艾维著.数学构模原理.海洋出版社，1985.4.姜启源.数学模型.高等教育出版社，1987.5.任善强.数学模型.重庆大学出版社，1987.6.M.Braun,C.S.Coleman,D.A.Drew,微分方程模型.朱煜民、周宇虹译，国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第一卷），1988.7.谌安琦.科技工程中的数学模型.中国铁道出版社，1988.8.江裕钊、辛培清.数学模型与计算机模拟.电子科技大学出版社，1989.9.杨启帆、边馥萍.数学模型.浙江大学出版社，1990.10.董加礼、曹旭东、史明仁.数学模型.北京工业大学出版社，1990.11.唐焕文、冯恩民、孙育贤、孙丽华.数学模型引论.大连理工大学出版社，1990.12.姜启源.数学模型（第二版）.高等教育出版社，1991.13.H.P.Williams,.数学规划模型建立与计算机应用.国防工业出版社，1991.14.李文.应用数学模型.华中理工大学出版社，1993.15.叶其孝主编.大学生数学建模竞赛辅导教材.湖南教育出版社，1993.16.寿纪麟.数学建模—方法与范例.交通大学出版社，1993.17.叶其孝.建模教育与国际数学建模竞赛.《工科数学》杂志社，1994.18.濮定国、田蔚文主编.数学模型.东南大学出版社，1994.19.欧阳亮.系统科学中数学模型.山东大学出版社，1995.20.陈义华.数学模型.重庆大学出版社，1995.21.朱思铭、李尚廉.数学模型.中山大学出版社，1995.22.蔡常丰.数学模型建模分析.科学出版社，1995.23.徐全智、杨晋浩.数学建模入门.电子科技大学出版社，1996.24.沈继红、施久玉、高振滨、张晓威.数学建模.哈尔滨工程大学出版社，1996.25.任善强、雷鸣.数学模型.重庆大学出版社，1996.26.齐欢.数学模型方法.华中理工大学出版社，1996.27.王树禾.数学模型基础.中国科学技术大学出版社，1996.28.李尚志主编.数学建模竞赛教程.江苏教育出版社，1996.29.南京地区工科院校数学建模与工业数学讨论班.数学建模与实验.河海大学出版社，1996.30.谭永基、俞文？.数学模型.复旦大学出版社，1997.31.D.Burghes.数学建模—来自英国四个行业中的案例研究，叶其孝、吴庆宝译.世界图书出版公司，1997.32.叶其孝主编.大学生数学建模竞赛辅导教材（二）.湖南教育出版社，1997.33.刘来福、曾文艺.数学模型与数学建模.北京师范大学出版社，199734.S.J.Brams,W.F.Lucas,P.D.Straffin,Jr..政治及有关模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第二卷），199735.W.F.Lucas,F.S.Roberts,R.M.Thrall.离散与系统模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics一书的第三卷），199736.H.Marcus-Roberts,M.Thompson.生命科学模型.国防科技大学出版社（本书为W.F.Lucas主编的ModulesinAppliedMathematics 一书的第四卷），199737.叶其孝主编.大学生数学建模竞赛辅导教材（三）.湖南教育出版社，199838.袁震东数学建模.华东师范大学出版社，199739.贺昌政.数学建模导论.成都科技大学出版社，199840.费培之.数学模型实用教程.四川大学出版社，199841.郭锡伯、徐安农.高等数学实验课讲义.中国标准出版社,199842.H.B.Griffiths,A.Oldknow.模型数学.萧礼、张志军编译，科学出版社，199843.乐经良.数学实验.高等教育出版社，199944.萧树铁主编.数学实验.高等教育出版社，1999.45.李尚志.数学实验.高等教育出版社，1999.46.谢云荪等.数学实验.科学出版社，199947.吴翊等.数学建模的理论与实践.国防科技大学出版社，199948.周义仓.数学建模实验.西安交通大学出版社，199949.朱道元.数学建模精品案例.东南大学出版社，199950.雷功炎.数学模型讲义.北京大学出版社，199951.朱建青.数学建模.解放军出版社，199952.边馥萍.工科基础数学实验.天津大学出版社，199953.贾晓峰.微积分与数学模型.高等教育出版社，199954.赵静等.数学建模与数学实验，高等教育出版社，施普林格出版社，200055.龚劬,、刘琼荪、何中市、傅鹂.数学实验.科学出版社，200056.白其峥.数学建模案例分析.海洋出版社，200057.蔡锁章等.数学建模原理与方法.海洋出版社.200058.杨学桢.数学建模方法.河北大学出版社，200059.王庚.实用计算机数学建模.安徽大学出版社，200060.魏平等.数学实验.吉林人民出版社，200061.钟尔杰.实用数值计算方法.高等教育出版社，200162.杨振华、郦志新.数学实验科学出版社，200163.叶其孝主编.大学生数学建模竞赛辅导教材（四）.湖南教育出版社，200164.全国大学生数学建模竞赛组委会.大学数学建模的理论与实践–2001中国大学生数学建模夏令营.湖南教育出版社，200165.钟尔杰.数学实验简明教程.电子科技大学出版社，200166.何万生、李万同.数学模型与建模.甘肃教育出版社，200167.何万生.数学模型与建模.甘肃教育出版社，2001.68.胡良剑、丁晓东、孙晓君.数学实验——使用MATLAB.上海科学技术出版社，200169.张兴永.数学建模简明教程.中国矿业大学出版社，2001.70.宋世德、郭满才、王经民、边宽江等..数学实验.高等教育出版社，200271.杨振华、郦志新.数学实验.科学出版社，200272.刘新平、魏暹逊等.数学建模导论.陕西师范大学出版社，200273.何文章、宋作忠.数学建模与实验.哈尔滨工程大学出版社，200274.刘来福、曾文艺.数学模型与数学建模.北京师范大学出版社，200275.周晓阳、谢松发、梅正阳.数学实验与MATLAB.华中科技大学出版社，200276.袁震东、蒋鲁敏、束金龙.数学建模简明教程.华东师范大学出版社，200277.刘承平.数学建模方法.高等教育出版社，200378.徐全智、杨晋浩.数学建模.高等教育出版社，200379.姜启源.、谢金星、叶俊.数学模型（第三版）.高等教育出版社，200380.魏贵民、郭科.理工数学实验.高等教育出版社，200381.万福永、戴浩晖.数学实验教程.科学出版社，200382.朱道元.数学建模案例精选.科学出版社，2003.83.李秀珍、庞常词、韦忠礼、黄福同.数学实验.中国农业科学技术出版社，200384.谢兆鸿、范正森、王艮远.数学建模技术.中国水利水电出版社，200385.赵红革.高等数学教材（含数学实验）.经济日报出版社，200386.蔡锁章等.数学建模.林业出版社，.200387.薛长虹等.大学数学实验.西南交通大学出版社，200388.朱建青.数学建模方法.郑州大学出版社，200389.杨瑞琰等.数学建模入门.中国地质大学出版社，200390.孙卫、张宇萍.高等数学实验.西北工业大学出版社，200391.杨策平.经济数学模型分析.中国地质大学出版社，200392.袁震东等.数学建模方法.华东师范大学出版社，200393.赫孝良、戴永红、周义仓.数学建模竞赛赛题简析与论文点评.西安交通大学出版社，200394.李尚志等.数学实验（第二版）.高等教育出版社，200495.王向东.数学实验.高等教育出版社，200496.李亚杰.数学实验.高等教育出版社，200497.刘琼荪等.数学实验.高等教育出版社，200498.张国权.数学实验.科学出版社，200499.马知恩、周义仓.传染病动力学的数学建模与研究.科学出版社，2004100.杨静化、韩可勤.医药数学建模教程.科学出版社，2004101.颜文勇.高等数学及实验.科学出版社，2004102.赵红革.经济数学教材（含数学实验）.经济日报出版社，2004103.何文章,、桂占吉、贾敬.大学数学实验.哈尔滨工程大学出版社，2004104.刘振航.数学建模.中国人民大学出版社，2004105.王兵团.数学建模基础.清华大学出版社，2004106.李继玲等.数学实验基础.清华大学出版社，2004107.李继玲、沈跃云、韩鑫.数学实验基础.清华大学出版社，2004108.薛毅.数学建模基础.北京工业大学出版社，2004109.郎艳怀等.经济数学方法与模型教程.上海财经大学出版社，2004110.甘筱青、陈涛、陈钰菊.数学建模教育及竞赛.江西高校出版社，2004111.赵东方.数学实验与数学模型.华中师范大学出版社，2004112.李林、周永正、煮祖庆、詹棠森.数学实驼与数学建模教程.中国林业出版社,2004113.王冬琳.数学建模及实验.国防工业出版社,2004114.张珠宝等.数学实验与数学建模.高等教育出版社，2005115.边馥萍、侯文华、梁冯珍.数学模型方法与算法.高等教育出版社，2005116.苏海容副主编.数学模型与数学实验（高职高专用书）.高等教育出版社，2005117.韩中庚.数学建模方法及其应用.高等教育出版社，2005118.杨启帆等.数学建模.高等教育出版社，2005119.唐焕文、贺明峰.数学模型引论（第三版）.高等教育出版社，2005120.阮晓青、周义仓.数学建模引论.高等教育出版社，2005121.王正东、尹强.数学软件与数学实验.科学出版社，2005122.宋来忠主编.数学建模与实验.科学出版社，2005123.焦光虹.数学实验.科学出版社，2005124.孟军、尹海东.农业数学实验.科学出版社，2005125.F.R.Giordano,M.D.Weir,W.P.Fox.数学建模（第三版）.叶其孝、姜启源等译.机械工业出版社，2005126.M.M.Meerschaert.数学建模–方法与分析（第二版）.刘来福等译.机械工业出版社，2005127.吴建国主编.数学建模案例精编.中国水利水电出版社，2005128.马新生、陈涛、陈钰菊、廖川荣.高等数学实验教材.中国科技出版社，2005129.杨启帆等.数学建模竞赛——浙大学生获奖论文点评（1999-2004）.浙江大学出版社，2005130.姜启源.、邢文训、谢金星、杨顶辉.大学数学实验.清华大学出版社，2005131.谢金星、薛毅.优化建模与LINDO/LINGO软件.清华大学出版社，2005132.柏宏斌、陈德勤.数学实验.四川大学出版社，2005133.谭永基、蔡志杰、俞文鮆.数学模型.复旦大学出版社，2005134.熊启才.数学模型方法及应用.重庆大学出版社，2005135.杨尚俊.数学建模简明教程.安徽大学出版社，2005136.刘锋.数学建模.南京大学出版社，2005137.萧树铁主编.数学实验（第二版）.高等教育出版社，2006138.李继成、朱旭、李萍.数学实验.高等教育出版社，2006139.谭永基等.经济、管理数学模型案例教程.高等教育出版社，2006140.杨启帆等.数学建模案例集.高等教育出版社，2006141.胡良剑、孙晓君.MATLAB数学实验.高等教育出版社，2006142.万福永、戴浩晖、潘建瑜.数学实验教程-MATLAB版.科学出版社，2006143.焦光虹.数学实验.科学出版社，2006144.董臻圃主编.数学建模方法与实践.国防工业出版社，2006145.陈汝栋、于延荣.数学模型与数学建模.国防工业出版社，2006146.张兴永、朱开永.数学建模.煤炭工业出版社，2006147.曹喜望.管理科学中的数学模型.北京大学出版社，2006.148.王兵团.数学实验基础（修订本）.清华大学出版社，2006149.湖北省大学生数学建模竞赛专家组.数学建模（本科册）.华中科技大学出版社，2006150.张学山、江开忠、李路.高等数学实验.华东理工大学出版社，2006151.赵红革、王为洪等.高等数学教材（含数学实验）.北京交通大学出版社，2006152.李伯德.数学建模方法.甘肃教育出版社，2006153.黄世华.数学建模基础教程.甘肃教育出版社,，2006154.任善强、雷鸣.数学模型（第二版修订版）.重庆大学出版社，2006155.刘新平、陈斯养等.全国大学生数学建模竞赛获奖论文集.陕西师范大学出版社，2006156.李辉来、刘明姬等.数学实验.高等教育出版社，2007157.姜启源、谢金星主编.数学建模案例选集.高等教育出版社，2007158.全国大学生数学建模竞赛组委会.数学建模的实践—2006年全国大学生数学建模夏令营论文集.高等教育出版社，2007 159.赵静、但琦主编.数学建模与数学实验（第三版）.高等教育出版社，2007160.戴明强、李卫军、杨鹏飞.数学模型及其应用.科学出版社，2007161.袁新生.lingo和excel在数学建模中的应用.科学出版社，2007162.韩中庚.数学建模竞赛获奖论文精选与点评.科学出版社，2007163.高隆昌、杨元.数学建模基础理论.科学出版社，2007164.彭放等、数学建模方法.科学出版社，2007165.肖海军.数学实验基础.科学出版社，2007166.蔡光兴、金裕红.大学数学实验.科学出版社，2007167.江世宏.MATLAB语言与数学实验.科学出版社，2007168.高等教育出版社2008年12月赵东方.数学模型与计算.科学出版社，2007169.冯杰等.数学建模原理与案例.科学出版社，2007170.宋世德、郭满才.数学实验.中国农业出版社，2007171.李志林、欧宜贵.数学建模及典型案例分析.化学工业出版社，2007172.吴礼斌、李柏年.数学实验与建模.国防工业出版社，2007173.李宏艳、王雅芝.数学实验（第二版）.清华大学出版社，2007174.薛毅、陈立萍.统计建模与R软件.清华大学出版社，2007175.陈理荣.数学建模导论.北京邮电大学出版社，2007176.周义仓、赫孝良.数学建模实验（第二版）.西安交通大学出版社，2007177.赵临龙.全国数学建模竞赛—高职高专大学生获奖论文点评（2002-2006年）.中国人民大学出版社，2007 178.罗万成等.大学生数学建模案例精选.西南交通大学出版社，2007179.杨桂元等.数学模型应用实例.合肥工业大学出版社，2007180.薛南青.数学建模基础理论与案例精选.山东大学出版社，2007181.数学建模走进中学课堂（VCD）.中央广播电视大学音像出版社，2007182.贾晓峰、魏毅强、王希云.微积分与数学模型.高等教育出版社.，2008183.孙浩等.数学建模简明教程.高等教育出版社，2008184.徐全智.数学建模（第二版）.高等教育出版社，2008185.陈恩水、王峰.数学建模与数学实验.科学出版社2008186.汪晓银、邹庭荣.数学软件与数学实验.科学出版社，2008187.刘焕彬等.数学模型与实验.科学出版社，2008188.王庚、王敏生.现代数学建模方法.科学出版社，2008189.王树禾.数学模型选讲.科学出版社，2008190.陶凤燕等.对应分析数学模型及其应用.科学出版社，2008191.陆志奇、李静.竞争数学模型的理论研究.科学出版社，2008192.朱道元.数学建模.机械工业出版社，2008193.李秀珍等.数学实验.机械工业出版社，2008194.刘三阳主编.数学建模.电子工业出版社，2008195.刘保东等.数学建模与数学实验.人民邮电出版社，2008196.重庆邮电大学数学建模组.数学建模素材选编.人民邮电出版社，2008197.王文波.数学建模及其基础知识详解.武汉大学出版社，2008198.张圣勤.数学建模与数学实验.复旦大学出版社，2008199.任善强、雷鸣、肖剑、周寅亮.数学模型.重庆大学出版社，2008200.王连堂主编.数学建模.陕西师范大学出版社，2008201.肖华勇.基于MATLAB和LINGO的数学实验.西北工业大学出版社，2008202.朱旭、李换琴、籍万新.MATLAB与基础数学实验.西安交通大学出版社，2008203.雷功炎.数学模型八讲——模型、模式与文化.北京大学出版社，2008204.叶其孝主编.大学生数学建模竞赛辅导教材（五）.湖南教育出版社，2008205.李大潜主编.中国大学数学建模竞赛(第三版).高等教育出版社,2008.《工程数学学报》编辑部:地址：西安交通大学理学院;邮编： 710049 ;电话： (029)82667877。
人教版《义务教育课程标准实验教科书 数学三年级上册》介绍
人教版《义务教育课程标准实验教科书数学三年级上册》介绍课程教材研究所小学数学课程教材研究开发中心课程教材研究所小学数学课程教材研究开发中心编写的《义务教育课程标准实验教科书数学（1～6年级）》，是以《全日制义务教育数学课程标准（实验稿）》（以下简称《数学课程标准》）的基本理念和所规定的教学内容为依据，在总结原九年义务教育小学数学教材研究和使用经验的基础上编写的。
本套的各册教材已经陆续通过全国中小学教材审查委员会的审查，并于2001年9月进入新一轮课程改革实验区开始使用。
从近5年来所收集到的各种反馈信息看，这套实验教材受到广大教师、学生和家长的普遍好评，在体现《数学课程标准》的改革理念、促进课堂教学的改革、满足各地教育发展需求等方面都能起到了很好的作用。
《义务教育课程标准实验教科书数学三年级上册》的研究与编写，坚持“在体现新理念的同时注意具体措施的可行性”“处理好继承与发展的关系”两个基本原则，力求使实验教材具有创新、实用、开放的特点。
注意符合教育学、心理学的原理和学生的年龄特征，关注学生的兴趣和经验，体现数学知识的形成过程，努力为学生的数学学习提供生动活泼、主动求知的材料与环境；使学生在获得数学基础知识、形成基本技能的同时得到情感、态度、价值观的熏陶与培养，促进学生的全面而富有个性的发展。
本实验教材具有下面几个明显的特点。
1．改进笔算教学的编排，体现计算教学改革的理念，重视培养学生的数感。
计算是帮助人们解决问题的工具，是小学生学习数学需要掌握的基础知识和基本技能。
本册实验教材的教学中有接近二分之一的内容是计算的教学内容（27课时），并且大量的是笔算的教学内容。
在当前的义务教育数学课程改革中，笔算是被削弱的内容，不仅“降低了笔算的复杂性和熟练程度”，《数学课程标准》中还提出：提倡算法多样化、避免程式化地叙述“算理”的改革理念等。
本册实验教材在处理笔算教学内容时，注意体现《数学课程标准》计算教学改革的理念，在内容编排的顺序、例题的安排、素材的选择等各个方面都采取了新的措施。
军用仓库的租用模型
楚雄师范学院2013年首届“雁峰杯”数学建模竞赛论文题目军用仓库的租用的优化模型队员姓名系别专业班级1 杨环数学系数学与应用数学 10级1班2 张瑞数学系数学与应用数学 10级1班3 刘小榕数学系数学与应用数学 10级2班2013年5月24日军用仓库的租用的优化模型摘要：本文建立了租用仓库的最优化签订合同模型，为合理签订合同，减少部队的租金支出提供最优化方案。
首先对问题进行分析可知首要任务是假设决策变量建立使得租金最少的目标函数，本文将仓库租用模型确定为线性规划问题。
其次对约束条件进行分析，得到租用的时间和租用的面积数为制约租金的两大因素。
基于这两大因素，本文在满足部队对仓库面积需求的情况下，考虑签订若干份合同，使部队可以享受最大的折扣，租金最少，尽量减少浪费多租用的面积。
接着本文对结果、灵敏度进行分析，寻找多种解决方法，并对模型做出评价和改进。
关键词：优化模型最少租金线性规划 LINGO求解某部队因战备训练任务需要,在今后半年内需租用地方仓库存放军事物资.已知每个月所需仓库的面积大小不同,多租了不用造成浪费,少租了会影响训练任务的完成.根据租用条件要求,仓库租用费用是随合同期限而定的,期限越长折扣越大,具体每月的仓库需求量和租金额如表1所和表2所示.租用仓库的合同每月初都可办理,每份合同具体规定租用面积数量和期限.因此,该部队可以根据实际需求在任何一个月初办理租用合同,每次办理时可签一份,也可以签若干份租用面积和期限不同的合同.试问该部队在保障训练任务需求的情况下,如何办理仓库的租用合同使总的租金最少?表1 每个月的仓库需求数量月份 1 2 3 4 5 6 所需仓库面积/100m 215 10 20 15 18 25表2 仓库的租期与租金月份1个月 2个月 3个月 4个月 5个月 6个月 合同期限内的租金/(元/100m 2)280045006000730084009300二、符号说明与基本假设2.1符号说明ij x ：第i 月份签订的期限为j 个月的合同（例如11x 代表一月份签订的期限为一个月的合同）；j a ：期限为j 个月所需支付的租金； j b ：未折扣时租用期限为j 个月所需总金额； j a ：折扣后租用j 月平均每月所需支付金额；j b ：未折扣时平均每月所需支付金额。
中学数学实验教材
中学数学实验教材摘要：由算术到代数是第一个重大转折.关键在于...全套教材共分六册,第一册是代数,在...除在代数课中加强理论和论证因素以外,在...(三)教学结构应当是完整性与发展性的...关键词：代数,性类别：专题技术来源：牛档搜索（）本文系牛档搜索（）根据用户的指令自动搜索的结果，文中内涉及到的资料均来自互联网，用于学习交流经验，作品其著作权归原作者所有。
不代表牛档搜索（）赞成本文的内容或立场，牛档搜索（）不对其付相应的法律责任！《中学数学实验教材》网络转载《中学数学实验教材》的编写、实验与研究为了进一步改革中学数学教育，教育部委托北京师大牵头，会同数学所、人教社、北京师院、景山学校等单位参照美国加州大学伯克利分校项武义教授的设想从1978年11月开始编写并实验研究另一套中学数学教材——《中学数学实验教材》（以下简称《实验教材》），这套教材不在编写、实验与研究之中，现在仅对教材的内容结构、实验情况作一概述。
一、教材的指导思想和体系结构《实验教材》的指导思想是：“精简实用，返朴归真，顺理成章，深入浅出。
”“精简实用，返朴归真”是选取内容的原则。
“精简实用”是个基本的指导思想，它恰当地表现了理论和实际的正确关系。
由实际到理论，就是由繁到简，把实际中多样的事物、现象经过分析、综合，归纳出简单而又具有普遍性的道理。
而只有精而简的理论才能用来“以简驭繁”。
所以“精简实用”在科学上的意义就是要求真正具有普遍性、简明扼要的理论。
要做到精简，必须抓住重点。
教材中，普遍实用的基础部分，那些有普遍意义的通性、通法就是重点。
数学是量科学。
基础数学的对象是数、空间、函数，相应的是代数、几何、分析三个学科。
这三者是各成体系但又密切联系的。
中学数学课应当是这三科的恰当配合的整体，中学数学课要从这三科中精选内容。
代数的重要内容有四个：①数系：有理数系、实数系、复数系，在中学阶段重点的是实数系。
最普遍有用的是数系的运算律（“数系通性”）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3-13王向东数学实验课本实验十三商品需求量的预测【实验目的】1．了解回归分析的基本原理和方法。
2．学习用回归分析的方法解决问题，初步掌握对变量进行预测和控制。
3．学习掌握用MATLAB命令求解回归分析问题。
【实验内容】现有某种商品的需求量、消费者的平均收入、商品价格的统计数据如表1所示，试用所提供的数据预测消费者平均收入为1000、商品价格为6时的商品需求量。
【实验准备】 206现实生活中，一切事物都是相互关联、相互制约的。
我们将变化的事物看作变量，那么变量之间的相互关系，可以分为两大类：一类是确定性关系，也叫作函数关系，其特征是一个变量随着其它变量的确定而确定，如矩形的面积由长宽确定；另一类关系叫相关关系，其特征是变量之间很难用一种精确的方法表示出来，如商品销量与售价之间有一定的关联，但由售价我们不能精确地计算出销量。
不过，确定性关系与相关关系之间没有一道不可逾越的鸿沟，由于存在实际误差等原因，确定性关系在实际问题中往往通过相关关系来体现；另一方面，当对事物内部规律了解得更加深刻时，相关关系也可能转化为确定性关系。
1．回归分析的基本概念回归分析就是处理变量之间的相关关系的一种数学方法，它是最常用的数理统计方法，能解决预测、控制、生产工艺化等问题。
由相关关系函数确定形式的不同，回归分析一般分为线性回归、非线性回归和逐步回归，在这里我们着重介绍线性回归，它是比较简单的一类回归分析，在实际问题的处理中也是应用得较多的一类。
207回归分析中最简单的形式是为标＋（、＝＋???yy xx01 1）量）（称自变量固定的未知参数，称为回归系数，??x01是均值为零的随机变量，它是其为回归变量，?的影响，是不可观察的，我们称他随机因素对y是为一元线性回归。
它的一个自然推广是（1）x多元变量，形如＋＋＋…＋＝???xx y mm0112）（?我们称为多元线性回归，或者更有一般地≥2，m＋＋＝＋…??)xf(y011（3）＋??)f(x mm）是＝（其中，…，），，…，＝1（)xf(xx j mx jm1（也叫曲线或曲面回称为非线性回归已知函数，作变量替换，一般能。
不难看出，对自变量归）x）的形）转化为线性回归（2够将非线性回归（3所以我们着重讨论线性回归的式进行求解分析，内容。
对（2）式两边同时取数学期望得，＝0（＋＝????DEYX＝））（42?其中 (1)x1m y1………X 208＝…Y…1xx nm1n y n T，）＝（，，…，????m01T），，…，＝（????n12）式称为线性回归方程。
线性回归分析所要4（考虑的主要任务是：用试验值（样本值）对未知同时对估计值作假设检验，作点估计，参数和2??＝从而确立与，…，之间的数量关系；在xxx y m01作）处对值作预测与控制，即对（，…，xx yy0m01这里我们均假设样本容量大于变量个区间估计。
＋＞1。
数，即mn2．模型的参数估计和假设检验用最小二乘法估计模型（4）中的参数，作离差平方和n＝＝?2?Q i1i?n （5）?2???)x??.....y(x??imi01mi11i?求使得达到最小。
根据微积分学中求极值的?Q方法，只需求关于，，…，一阶导数为0???Q m01的真值，，…，的方程组的解，此解不是，???m01 ，…，的最小二乘估计值，我们用，而是????1m0表示 ＝T?1T?YXX)X(）（6 ）将4，的估计值代入回归方程（，…，????1m0 209得到的估计值y ＝＋＋…＋ ???xxy1m1m0）（7的可作为随机误差拟合误差＝－称为残差， ?e y y估计，而nn＝＝ ??22y)?e(yQ iiii?1i?1（8）。
为残差平方和（或剩余平方和），即?)Q(在实际问题中，事先我们并不知道或者不能断定随机变量与一组变量，…，之间有线性关xx y m1往往只＋）式＝＋＋…＋系，如（2????xx y mm011还须是一种假设，因此在求出线性回归方程后，对求出的线性回归方程同实际观测数据拟合效果进行检验，可提出以下原假设：＝…＝：＝＝0???H0m01（9）检验法（详细内容在数理统计采用检验法或RF，，拒绝类书籍中均可查到，此处不再赘述）H0之间显著地有线性关系；否则认为，…，与xx y m1之间线性关系不则就接受与，…，，认为Hxx y0m1显著。
3．变量的预测与控制可由给当回归模型和系数通过了假设检验后，是随机的，，…，＝（定的，）预测出yyxxx0m00010）知道，其预测值（点估计）7显然由回归方程（为 210＝＋＋…＋ ???yxx1m0001m0 10（）的预测区间对于给定的显著水平，可以算出ya0接近较大且（区间估计），结果较复杂，但当xni0平均值，的预测区间可简化为yx0i［－，＋］ yy susu00aa??1122）（11a分位数。
－是标准正态分布的1 其中u a2?12对于的区间估计方法可用于给出已知随y0的置信区间，－服从均值为机数据的残差＝ ee y y的置信区间不包括零的正态分布，所以若某个e i零点，则认为这个数据是异常的，可予以剔除。
MATLAB统计工具箱中的回归分析命令4．多元线性回归模型（4）可采用命令regress，此命令也可用于求解一元线性回归，其格式如下所示：211，格式如下：多元二项式回归用命令rstool212对于非线性回归模型的求解命令我们也一来，nlpredcinlintool并给出，可用命令nlinfit，实现，其格式如下：【实验方法与步骤】 213．引例问题的分析求解1商我们可以初步判断，由问题提供的数据，品的需求量与消费者的平均收入和商品价格之具体的函数关系式我们还间存在某种相关关系，我们先独立分析商品需不清楚。
输入三组数据，商品需求量与价格之间求量与消费者平均收入，存在何种关系：1100 400 1300 1200 500 300 >> x1=[1000 600消费者的平均收入1300 300]';%商品价格>> x2=[5 7 6 6 8 7 5 4 3 9]';%商>> y=[100 75 80 70 50 65 90 100 110 60]';% 品的需求量以消费者的平均收入和商>> plot(x1,y,'+')% 品的需求量所对应的离散点作图>> plot(x2,y,'+')%以商品的价格和商品的需求量所对应的离散点作图2141201008060409783456由上面两图我们看到商品的需求量随着消费者平均收入增加呈线性递增的趋势，而随着商品的价格增加呈线性递减趋势，这样我们可初步判断商品需求量与消费者平均收入和商品价格之间存在某种线性相关的关系。
接下来用多元线性回归来进行分析检验：>> x=[ones(10,1) x1 x2];>> [b,bint,r,rint,stats]=regress(y,x)b =111.6918 0.0143 -7.1882bint =56.0503 167.3334-0.0120 0.0406-13.2306 -1.1458stats =0.8944 29.6533 0.0004可知回归系数＝111.6918，＝0.0143，＝ 012215均包含了回归bint，-7.1882，它们的置信区间为第三0.8944，系数的估计值，stats第一个分量为，说明回归方，拒绝H0.0004＜0.05p 个分量＝0 0，线性回归方程模型程系数不为－0.0143＝111.6918＋x y1 12）（7.1882x2成立。
继续对残差进行分析，作残差图：>> rcoplot(r,rint)3020100-10-2012345678910大多数数据的残差离零从残差图可以看出，点较近，且残差的置信区间全部包含零点，这进一步说明回归模型（12）能近似地符合原始数据。
现利用线性回归方程对引例问题的要求作出预测，＝1000，＝6xx12>> z=111.6918+0.0143*1000-7.1882*6z =82.8626得到结果，当消费者平均收入为1000、商品价格为6时的商品需求量大约为82.8626。
【结果分析】 216stats利用线性回归分析所得结果，我们看到，且部1第一个分量为0.8944，它并不十分接近分残差离零点较远，这说明回归模型还存在缺我陷，几个随机变量之间的线性关系有待改进，们不妨用多元二项式回归来试验：>> x=[x1,x2];>> rstool(x,y,'purequadratic') 140120100806040204006008001000120045678得到一交互式画面，左图是x2固定时曲线y(x1)及置信区间，右图是x1固定时曲线y(x2)及置信区间。
在x1，x2指示框中分别输入1000和6，即预测到平均收入为1000、价格为6时商品需求量为88.4791。
在下拉列表框Export中选择“all”，把beta（回归系数）、rmse（剩余标准差）和residuals（残差）传送到MATLAB工作区，在命令框中输入>> beta,rmse,residuals217即可得beta、rmse、residuals的数值beta =110.53130.1464 -26.57091.8475 -0.0001rmse =4.5362、linear下拉列表菜单对在Model模型比purequadratic、interaction、quadratic4型的剩余标较剩余标准差，其中purequadratic个模型的剩余标准差最准差4.5362相比其它3，故此回归模型的显著性较好。
我们用接近于0纯二次回归模型所得的残差与前面线性回归模型所得的残差列表进行比较显然由二元纯二次多项式所得残差绝大多数要比由线性回归模型所得残差更接近零点，由最小二乘法原理我们可以相信，改进后的回归模型＝110.5313＋0.1464－x y1 1.8475＋26.5709－0.000122xxx212 218能够更好地近似原始数据。
【练习与思考】．电影院调查电视广告费用和报纸广告费用对1建立回归模得到下面的数据，每周收入的影响，型并进行检验，诊断是否有异常点。
每周收96 90 95 92 95 95 94 94 入电视广1.5 2.0 1.5 2.5 3.3 2.3 4.2 2.5 告费用报纸广5.0 2.0 4.0 2.5 3.0 3.5 2.5 3.0告费用2．由成年女子身高与裤长的样本，研究成年女子身高与裤长的潜在关系。