扭转强度计算
(仅供参考)第十九章-扭转的强度与刚度计算
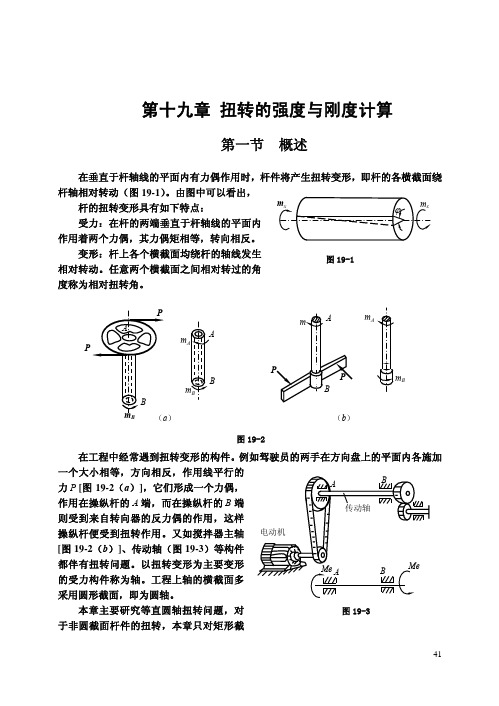
一、外力偶矩的计算
前面已经指出 ,使轴产生扭转变形的是外力偶矩。但是作用于轴上的外力偶矩往
往不是直接给出的,而是给定轴所传递的功率和轴的转速。以图 19-3 所示的传动轴为例,
由电动机的转速和功率可以求出传动轴 AB 的转速及通过皮带轮输入的功率。功率由皮
带轮传到轴 AB 上,再经右端的齿轮输出。设通过皮带轮给 AB 轴输入的功率为 N(kW),
因为 1kW=1000N·m/s 因此每秒钟输入功应为 : W = N ×1000(N ⋅ m)
(a)
电动机是通过皮带轮以力偶矩 Me 作用于 AB 轴上的,若 AB 轴的转速为每分钟 n 转,
则力偶矩 Me 在每秒内完成的功应为 :
W = 2π × n × Me(N ⋅ m)
(b)
60
因为 Me 所完成的功也就是皮带轮给 AB 轴输入的功,故(a)、(b)两式应相等,这
据微元的平衡要求,不仅左右一对面上有大小相等,方向相反的剪应力 τ ,在上下一对
面也必须有剪应力τ ′ ,而且由力矩平衡条件 ∑ mz = 0 有:
(τtdy)dx = (τ ′tdx)dy
由此得到:
τ =τ′
(19-2)
这表明,在相互垂直的两个微面上,剪应力总是成对出现的,它们数值相等,而方
向均垂直于两微面的交线,或指向或背离这一交线。这就是剪应力互等定理。
利用第三节中的(b)式和(c)式,上式可以写成:
φ
φ
图 19-9
u = 1 τγ 2
再由剪切胡克定律(式 19-3)得:
u = 1 τγ = τ 2 2 2G
46
第四节 圆轴扭转时的应力与变形
一、横截面上剪应力计算公式
圆轴扭转时,在已知横截面上的扭矩后,还应进一步研究横截面上的应力分布规律,
扭转—扭转轴的应力及强度计算(建筑力学)
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
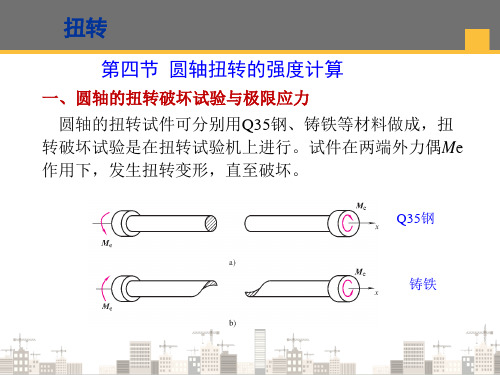
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
扭转时的强度计算.

一、强度计算
1 强度条件: 塑性材料: 脆性材料:
Mn max WP 0.5 0.6
0.8 1.0
2 强度计算的三个方面: a、强度校核 b、截面选择 c、许可荷载确定
• 例1
• • • •
Wp
D3
1 16
4
d 90 2 2.5 0.944 D 90
4 3
•将
得
Wp
903
16
1 0.944 29400m m ,代入上式,
Mn 1.5 103 51MPa 60MPa max 9 Wp 2940010
• 所以 该轴满足强度条件。如图为一钢圆轴,两端受外力偶m的作用,已知m=2.5 ,
Mn
KN.m,直径d=60m,许用应力为60MPa。试校核该轴的强度。 由平衡条件,得 (2) 校核强度 由公式 max
• 解:(1 )计算扭矩
M n m 2.5KN .m
Mn ,得 WP
M n M n 2.5 103 16 max 2 59MPa 60MPa 2 W p d 6 10 16
•
所以,满足强度要求。
• 例2 如图为某汽车传动轴简图,传递的最大力矩m=1.5KN.m,
• • 轴为无缝钢管,外径D=90mm,厚T=2.5mm,已知许用剪应 力 60MPa ,试校核该轴的强度。
解:1. 求扭矩Mn. 取脱离体如图(b).
M n 1.5kN.m 由平衡条件 M x 0 得: Mn •2. 强度校核 由公式 max W p •式中 Wp 是空心圆截面的抗扭截面模量
圆柱和圆筒扭转强度计算方法

圆柱和圆筒扭转强度计算方法1.圆柱的扭转强度计算方法:圆柱的扭转强度可以通过以下公式计算:T= τ_max × J其中,T为圆柱的扭矩,τ_max为圆柱所受到的最大剪应力,J为圆柱的极性矩。
a. 圆柱的最大剪应力(τ_max)计算:圆柱的最大剪应力可以通过以下公式计算:τ_max = T / (π × r^3)其中,T为圆柱的扭矩,r为圆柱的半径。
b.圆柱的极性矩(J)计算:圆柱的极性矩可以通过以下公式计算:J=(π×r^4)/2其中,r为圆柱的半径。
2.圆筒的扭转强度计算方法:圆筒的扭转强度可以通过以下公式计算:T = τ_max × J其中,T为圆筒的扭矩,τ_max为圆筒所受到的最大剪应力,J为圆筒的极性矩。
a. 圆筒的最大剪应力(τ_max)计算:圆筒的最大剪应力可以通过以下公式计算:τ_max = T / (2 × π × r^2 × t)其中,T为圆筒的扭矩,r为圆筒的内半径,t为圆筒的壁厚。
b.圆筒的极性矩(J)计算:圆筒的极性矩可以通过以下公式计算:J=(π×(r_o^4-r_i^4))/2其中,r_o为圆筒的外半径,r_i为圆筒的内半径。
需要注意的是,在计算圆筒的扭转强度时,需要考虑到圆筒的壁厚对扭转强度的影响。
因此,在计算圆筒的最大剪应力时,需要除以2×π×r^2×t的倍数。
以上就是圆柱和圆筒的扭转强度计算方法。
在实际应用中,还需根据具体的材料特性和工程要求进行参数的选择和计算。
扭转杆件的强度、刚度计算

12.3 扭转杆件的强度、刚度计算对受扭转的杆件,除了强度要求外,通常刚度也要同时考虑。
受扭杆件危险点均为纯剪切应力状态。
对纯剪切应力状态,可以证明,与第一强度理论对应的强度条件为≤(12-4)与第三、四强度理论对应的强度条件为≤(12-5)≤(12-6)式中,[τ]为许用切应力,它与许用正应力之间的关系为脆性材料[ τ ] = (0.8 ~ 1)[ σ ]塑性材料[ τ ] = (0.5 ~ 0.6)[ σ ]例12-4一钢传动轴如图12-4a所示,转速n = 208rpm,主动轮B的输入功率P=6kW,两个从动轮A、CB的输出功率分别为P A = 4kW,P c = 2kW。
已知:轴的许用应力[σ] = 60MPa,许用单位扭转角[ϕ]=1︒/m,切变模量G = 80GPa,试设计轴的直径d。
解:1.计算外力偶矩,绘扭矩图。
用截面法及扭矩符号的规定,得AB、BC段的扭矩分别为T AB = 183.6N·mT BC = -91.8N·m根据以上计算结果,作扭矩图如图12-4b所示2.按强度条件设计轴的直径由扭矩图可见,最大扭矩为T max = 183.6N·m,危险截面为AB段各横截面。
危险点在危险截面上周边各个点,处于纯剪切应力状态。
根据最大切应力理论,强度条件应为≤≤得 d ≥3.按刚度条件设计轴的直径由刚度条件式(12-2),扭转刚度条件为ϕmax = ≤[ ϕ]≤[ϕ]得d≥为了同时满足强度及刚度要求,应在以上两计算结果中取较大值作为轴的直径,即轴的直径应大于或等于34mm,可取d = 34mm。
例12-5实心圆轴横截面上的扭矩T = 5kN·m。
轴的许用应力[ ] = 87MPa,试按强度设计轴的直径D。
若将轴改为空心圆轴,且内外直径之比,试设计截面尺寸。
并比较实心圆轴和空心圆轴所需的材料用量。
解:本题按第四强度理论来设计。
对实心愿轴,由强度条件式(12-6)≤即≤得D≥取D = 80mm。
方形杆的扭转强度计算公式

方形杆的扭转强度计算公式引言。
在工程力学中,方形杆的扭转强度是一个重要的参数,它决定了材料在受到扭转力作用时的抗扭性能。
扭转强度的计算是工程设计中不可或缺的一部分,它可以帮助工程师确定材料的合适用途和设计结构的稳定性。
本文将介绍方形杆的扭转强度计算公式及其相关知识。
方形杆的扭转强度计算公式。
方形杆的扭转强度计算公式可以通过以下公式表示:T = k G θ / L。
其中,T表示扭转力,k表示形状系数,G表示剪切模量,θ表示扭转角度,L 表示杆的长度。
形状系数k是一个与杆的几何形状相关的参数,对于方形杆而言,其形状系数可以通过以下公式计算:k = 1.5 + 1.5 (d / b)。
其中,d表示杆的对角线长度,b表示杆的边长。
剪切模量G是一个描述材料抗扭性能的参数,它可以通过以下公式计算:G = E / (2 (1 + v))。
其中,E表示材料的弹性模量,v表示泊松比。
扭转角度θ是指在扭转过程中,杆的一端相对于另一端的旋转角度。
杆的长度L是指杆的长度。
以上公式是用来计算方形杆在受到扭转力作用时的扭转强度的基本公式。
通过这些公式,工程师可以计算出方形杆在不同扭转力下的变形情况,从而确定材料的合适用途和设计结构的稳定性。
相关知识。
在实际工程中,方形杆的扭转强度计算还需要考虑一些其他因素,例如材料的疲劳性能、温度影响、表面处理等。
这些因素都会对方形杆的扭转强度产生影响,因此在实际工程设计中,需要综合考虑这些因素。
此外,方形杆的扭转强度计算还需要考虑杆的端部支撑情况、杆的截面形状、杆的材料等因素。
这些因素都会对方形杆的扭转强度产生影响,因此在实际工程设计中,需要综合考虑这些因素。
结论。
方形杆的扭转强度计算是工程设计中一个重要的参数,它可以帮助工程师确定材料的合适用途和设计结构的稳定性。
通过合理计算方形杆的扭转强度,可以有效地预测材料在受到扭转力作用时的变形情况,从而保证工程结构的安全可靠性。
在实际工程设计中,需要综合考虑材料的疲劳性能、温度影响、表面处理、端部支撑情况、截面形状、材料等因素,以确保方形杆的扭转强度计算的准确性和可靠性。
扭转强度计算公式

扭转强度计算公式
扭转强度是指材料可以承受持续转变外力的能力,它也是衡量材料结构强度的一个重要指标。
由于它对于确定材料性能及其结构安全性起着重要作用,因此了解扭转强度和计算其值非常重要。
扭转强度的计算可以通过以下公式来实现:T=F * r / J,其中T为扭转强度,F为外力,r为外力的作用半径,J为扭转截面积矩,即材料主轴线上的横截面积。
通过上述公式可以看出,要计算扭转强度,必须先确定外力F和扭转截面积矩J的大小。
外力F是指作用在材料上的外力,可以通过实验来确定。
而扭转截面积矩J是指材料的横截面积,可以通过实验或理论计算来确定。
在实际应用中,扭转强度的计算还受到水平和垂直外力的影响,因此,在计算扭转强度时,必须考虑外力的方向和强度。
在计算扭转强度时还要考虑材料的尺寸、形状和结构,以及外力的作用点。
这些因素都会影响材料的扭转强度,因此,在计算扭转强度时,必须将这些因素考虑在内。
要计算材料扭转强度,必须先确定外力F和扭转截面积矩J,还要考虑材料尺寸、形状和结构以及外力方向和强度等因素。
通过恰当的计算,可以准确地测量出材料的扭转强度,从而为结构的安全性
提供可靠的参考。
扭转强度计算ppt

内容回顾
扭转变形受力特点
扭转内力名称及方向规定
内容回顾
扭矩的计算 截面法
作扭矩图
已知一等截面实心圆轴,受力如图,MA=60KN.M, MB=15KN.M,MC=25KN.M,MD=20KN.M,试作出扭矩图。
工程背景
工程背景
工程背景
6.3 扭转强度计算 ——思路
6.3 扭转强度计算 ——内容
T(或Mn)——横截面上的扭矩来自ρ——待求点到圆心的距离
Ip——截面对其形心的极惯性矩
IP 2dA
A
分析应力分布规律
横截面上任一点切应力大小同ρ呈正比
max
Tr Ip
Wp
Ip r
——抗扭截面系数
max
T Wp
思考及练习
思考: 实心圆轴纯扭转时,如何破坏? 从外向内,逐层破坏
练习: 例题6-2
MD 0.96kN m ,已知材料的许用切应力 80MPa
试校核该轴的强度。
解:用截面法求得BA、AC、CD段的扭矩,并
绘出扭矩图如图所示。
因为传动轴为等截面,所以最大切应力发生在 AC段内各截面周边上各点。
max
Tmax Wp
1.76103 N m
(0.05m)3
71.7 106 Pa
71.7MPa
16
因此,该轴满足强度条件。
拓展条件 总结步骤 解决例题6-3
作业布置
习题5-16 思考空心轴和实心轴的应用价值 预习下节内容——扭转变形及刚度计算
小结
扭转应力公式 扭转强度计算
再 见!
建立圆轴扭转时横截面上的应力公式 理解公式,分析应力分布规律 建立强度条件(类比轴向拉压变形) 应用解决强度计算问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考及练习
思考: 实心圆轴纯扭转时,如何破坏? 从外向内,逐层破坏
练习: 例题6-2
建立强度条件
横截面最大切应力不超过材料的许用切应力
τmax τ
τ max Tmax Wp
塑性材料: 0.5 0.6 脆性材料: 0.8 1.0
解:用截面法求得BA、AC、CD段的扭矩,并 绘出扭矩图如图所示。
因为传动轴为等截面,所以最大切应力发生在 AC段内各截面周边上各点。
max
Tmax 1.76 103 N m 71.7 106 Pa 71.7MPa Wp (0.05m)3 16
因此,该轴满足强度条件。
6.3 扭转强度计算 ——内容
建立圆轴扭转时横截面上的应力公式 理解公式,分析应力分布规律 建立强度条件(类比轴向拉压变形) 应用解决强度计算问题
建立圆轴扭转时 横截面上的应力公式
两个假设 平面假设 横截面间距不变假设 三种关系 变形几何关系 物理关系 静力学关系
2/6/2018
拓展条件 总结步骤 解决例题6-3
作业布置
习题5-16
思考空心轴和实心轴的应用价值
预习下节内容——扭转变形及刚度计算
小结
扭转应力公式
扭转强度计算
再
见!
强度计算理论
强度校核 截面设计 许用荷载计算
max
Tmax Wp
强度计算应用
补充例题:图示一直径为 d 50mm 的传动轴,外 力偶矩 M A 3.19kN m M B 1.43kN m M C 0.8kN m M D 0.96kN m ,已知材料的许用切应力 80MPa 试校核该轴的强度。
6.3 扭转强度计算
内容回顾
扭转变形受力特点
扭转内力名称及方向规定
内容回顾
扭矩的计算 截面法 作扭矩图
已知一等截面实心圆轴,受力如图,MA=60KN.M, MB=15KN.M,MC=25KN.M,MD=20KN.M,试作出扭矩图。
工程背景
工程背景
工程背景
6.3 扭转强度计算 ——思路
横截面上任一点切应力的计算公式 Tρ τρ Ip T(或Mn)——横截面上的扭矩 ρ——待求点到圆心的距离 Ip——截面对其形心Βιβλιοθήκη 极惯性矩I P 2 dA
A
分析应力分布规律
横截面上任一点切应力大小同ρ呈正比
max
Wp Ip r
Tr Ip
——抗扭截面系数 T max Wp
