§4随机变量函数的分布
随机变量函数的 分布

WENKU DESIGN
离散型随机变量函数的概率分布
01
定义
离散型随机变量函数的概率分布 是指随机变量取各个可能值的概 率。
02
03
计算方法
应用
根据随机变量的定义和性质,计 算每个可能值的概率,并列出概 率分布表。
在概率论和统计学中,离散型随 机变量函数的概率分布是描述随 机变量取值规律的重要工具。
离散型随机变量函数的期望和方差
1 2 3
期望
离散型随机变量函数的期望是指所有可能取值的 概率加权和,即E(X)=∑xp(x)。
方差
离散型随机变量函数的方差是每个可能取值的概 率加权平方和的平均值,即D(X)=∑x^2p(x)E(X)^2。
应用
期望和方差是描述离散型随机变量函数取值稳定 性和分散程度的指标,在统计学、决策理论和风 险管理中具有重要应用。
随机变量函数的定义
随机变量函数是指将一个随机试验的 结果映射到一个实数域上的函数。
随机变量函数通常用大写字母表示, 如X(ω),其中ω表示随机试验的结果。
随机变量函数的性质
确定性
对于每一个试验结果ω,随机变量函数都 有一个确定的函数值X(ω)。
VS
随机性
函数值X(ω)是随机的,即对于相同的试验 结果ω,每次试验都可能得到不同的函数 值。
随机变量函数的分布
https://
REPORTING
• 随机变量函数的基本概念 • 离散型随机变量函数的分布 • 连续型随机变量函数的分布 • 随机变量函数的变换 • 随机变量函数的应用
目录
PART 01
随机变量函数的基本概念
REPORTING
WENKU DESIGN
连续性
随机变量函数的分布

二 、连续型随机变量函数的分布 2.分布函数法 一般地,若已知X的概率密度为 fX(x),求其函数 Y=g(X)的概率密度 fY(y)分两个步骤: 10 根据分布函数的定义求Y的分布函数FY(y); 20 由 fY(y) = F (y) 求出 fY (y)
例3 对一圆片直径进行测量, 其值在[5,6]上均匀分
定理 设X是一连续型随机变量,其密度函数f(x) , (-∞<x< +∞ ),又函数y = g(x)处处可导,且严格单 调,其反函数为x = h(y ),则Y = g(X)也是一连续型随 机变量,且密度函数为
h y f[ h ( y )], y f y Y , 其他 0
计算离散型随机变量函数的分布的方法: 首先将xi的取值代入函数关系,求出随机变量Y相应的取值
y g ( x )( i 1 , 2 , .) i i
如果yi(i=1,2,…)的值各不相等,则Y的概率分布为 Y P y1 p1 y2 p2 … … yi pi … …
如果 yi=g(xi)(i=1,2,…)中出现m(≥2)个相同的函数值,即存在
0 , y25 /4 F (y) * 25 /4y9 1, y9
F ( y ) P { Y y } P { X / 4 y }
2
P { X 4 y / }
4 y /
f ( x ) dx X
例3 对一圆片直径进行测量, 其值在[5,6]上均匀分
其中, m g ( in{ ), g ( )}, m g ( ax ), g ( )
注意 若f(x)在有限区间[a,b]外等于0,则只需设在[a,b] ( x ) 0 [ 或 g ( x ) 0 ]. 上有 g
概率论随机变量的分布函数ppt课件

因此, A 是不可能事件
P{A} 0.
ppt课件
12
例1: 设随机变量X具有概率密度
ke 3 x
x0
f (x)
0 x0
(1)试确定常数k,(2)求F(x),(3)并求P{X>0.1}。
解: (1)由于
f (x)dx
ke3xdx k 1
,解得k=3.
0
3
于是X的概率密度为
f
(
x)
O
x
(3) 在 x= 处曲线有拐点,且以x轴为渐近线 ;
(4) 对固定的,改变的值,图形沿Ox轴平移;
(5) 对固定的,改变, 越小,图形越尖.
正态分布的分布函数为: F ( x)
ppt课件
1
2
e dt x
(t )2 2 2
28
标准正态分布
当=0, =1时,称X服从标准正态分布,记作X~N(0,1).
例3 设电阻值R是一个随机变量,均匀分布在800欧~1000
欧,求R的概率密度及R落在850欧~950欧的概率.
解: 由题意,R的概率密度为
1 f (r) 1000 800
, 800 r 1000
0
, 其它
950 1
而 P{850 X 950}
dr 0.5
200 ppt课件
850
18
2. 指数分布
注 (4)式及连续性随机变量分布函数的定义表示 了分布函数与概率密度间的两个关系.利用这些 关系,可以根据分布函数和概率密度中的一个推 出另一个.
ppt课件
10
连续型随机变量的分布函数与概率密度的几何意义:
1. F(x)等于曲线f(x)在(-∞,x]上的曲边梯形的面积。
4.4正态随机变量线性函数的分布

2. π
小结
1. 若X~N(,2), 则当 b0时,
YabX~N(ab,b22).
特别: X~N(0,1).
2. 随机变量 X与 Y相互独立,且 X~N(x,x2),
Y~N(y,y2),则 X Y ~ N (xy,x 2y 2 ).
推广: 设 X1,X2, Xn相互独立,且 Xi ~N(i,i2),
第四章正态分布正态随机变量的线性函数的分布44定理1设随机变量的线性函数bx时类似地可证
第四章
正态分布
§4.4 正态随机变量的线性函数的分布
[定理1] 设随机变量 X服从正态分布 N(,2),则 X
的线性函数 YabX (b0) 也服从正态分布:
Y a b~ X N (a b,b 22 ).
2.设随机变量 X服从正态分布 N(,2) ,且二次方程
y24yX0无实根的概率为0.5 , 则___.__
解: 方程 y24yX0无实根就是 1 6 4 X 0 ,
即X4,按题意,有 P (X 4 ) 0 .5,即 P (X4 )0 .5 .
已知 X~N(,2),所以
P (X 4 ) P (X 4 ) (4 ),
从而,
(4)0.5,
因为(0)0.5,所以应有
4
0,
由此得 4.
n
n
n
i1,2, ,n,则
ciXi ~N( cii, ci2 i2).
i1
i1
i1
思考题
1.设随机变量 X与 Y独立,且 X服从均值为1 , 标准差 为 2 的正态分布,而 Y服从标准正态分布,试求随机 变量 Z 2 X Y 3 的概率密度. 解:已知 X与Y独立,且X ~ N ( 1 ,2 ),Y ~ N ( 0 ,1 ),
随机变量函数的分布

此时,称Y服从自由度为1的χ2-分布。
变限函数求导公式:
b(x)
f
(t)dt
f b(x)b(x)
f a(x) a(x).
a(x)
例3:设r.v.X~U(0,1),求Y=eX的概率密度.
1, 0 x 1, 解:因r.v.X~U(0,1),故X的概率密度为:fX (x) 0, 其它.
如图, fX (x)的非零段将整个 x轴分为三部分:
(-∞,0),[0,1),[1,+ ∞); 从而,整个y轴相应地也被分为三 部分: (-∞,1),[1,e),[e,+ ∞).
因此,应就y分为上述三个区 间来求Y的分布函数.
(1) 当y<1时,再分为两种情形:
a) 当y≤0时,
FY (y) PY y P eX y
P() 0;
b) 当0< y<1时,
fY
(
y)
1 y
,
1 y e,
0, 其它.
注意:本题是重要题型,必须熟练掌握。
方法2 公式法(y=g(x)为单调可导函数)
定理:设连续型随机变量X的概率密度为
f X (x)( x )
函数g(x)处处可导且有恒有 g(x) 0(g(x) 0)
则Y=g(X)是连续型随机变量,且其概率密度为
◆如果Y各可能取值中存在多个值相等,则Y取该值的概 率为这些相等值对应的X取值的概率之和.
例如,当 yk g(xi ) g(x j ) g(xm ),
则由基本事件互斥性与概率可加性得:
PY yk P X xi P X xj P X xm
例1:设r.v.X的分布列为:
X
-1
012
P 0.2 0.3 0.1 0.4
4-4正态随机变量的线性函数的分布

1 fZ ( z) e 3 2
( z 5 ) 2 18
, z .
§4.4 正态随机变量的线性函数的分布
2.设随机变量 X 服从正态分布 N ( , 2 ) , 且二次方程
y 4 y X 0 无实根的概率为 0.5 , 则 _____. 解: 方程 y 2 4 y X 0 无实根就是 16 4 X 0 , 即 X 4, 按题意,有 P( X 4) 0.5 , 即 P( X 4) 0.5. 已知 X ~ N ( , 2 ) , 所以 X 4 4 P( X 4) P( ) ( ), 从而, 4 ( ) 0 .5 , 4 0 , 由此得 4. 因为 (0) 0.5 , 所以应有
i 1
i 1
i 1
前面,我们已经看到: 若X与Y独立,则X与Y不相关, 但由X与Y不相关,不一定能推出X与Y独立. 但对下述情形,独立与不相关等价 若(X,Y)服从二维正态分布,则
X与Y独立
X与Y不相关
§4.4 正态随机变量的线性函数的分布
小 结
1. 若 X ~ N ( , 2 ),则当b 0时,
fY ( y) [ FX ( y a )] 1 f X ( y a ) 1 e b b b 2 b
[ y ( a b )]2 2 b 2 2
,
所以Y ~ N (a b , b2 2 ). 当 b 0 时类似地可证.
§4.4 正态随机变量的线性函数的分布
2 推广: 设 X1 , X 2 , X n 相互独立, 且 X i ~ N ( i , i ),
i 1 , 2 , , n, 则
ci X i ~ N ( ci i , c i i 1 i 1 i 1
第四章 随机变量及其分布

第一节 随机变量及其分布函数
一、 随机变量的概念
1、含义:用来表示随机现象结果的变量。 ①样本点本身是用数量表示的; T ②样本点本身不是用数量表示的。 H 总之,不管随机试验的结果是否具有数量的性 质,都可以建立一个样本空间和实数空间的对 应关系,使之与数值发生联系,用随机变量的 取值来表示事件。 2、定义:定义在样本空间Ω={ω}上的实值 函数X=X(ω)称为随机变量,常用大写英文字 母或小写希腊字母来表示,相应地,用小写英 文字母表示其取值。
为了方便地表示随机事件的概率及其运算,我 们引入了分布函数的概念。
定义:设X 是一随机变量,对x R,
称F ( x ) P ( X x )为随机变量X的分布函数;
并称X 服从分布F ( x ),记为X ~ F ( x ).
注:(1)分布函数表示的是随机事件的概率。 (2)分布函数与微积分中的函数没有区别。
P ( X 0) F (0) F (0 0) 0.8 0.3 0.5 P ( X 1) F (1) F (1 0) 1 0.8 0.2
X P
1 0.3
0 0.5
1 0.2
思考:X还能取 到其他数值吗?
例4 一汽车沿一街道行驶,需要经过三个设有红绿信号 灯的路口,且信号灯的工作相互独立,以X表示汽车首 次遇到红灯已通过的路口数,求X的概率分布列。 解:记Ai—汽车在第i个路口遇到红灯,i=1,2,3. 1 P ( Ai ) P ( Ai ) , 且A1 , A2 , A3相互独立. 2 X的可能取值为 0, 1, 2, 3.
共有10个不同的样本点
记X表示“空格个数”,则有
X ( ) 2
X ( ) 1 X ( ) 0
随机变量的分布函数
x < −1 , −1 ≤ x < 2, 2 ≤ x < 3, x ≥ 3.
-1 0 1 2 3
4
1
x
§3
随机变量的分布函数
1 1 1 P{X ≤ } = F( ) = , 2 2 4 3 5 5 3 3 1 1 P{ < X ≤ } = F( ) − F( ) = − = , 2 2 2 2 4 4 2
9
§3
随机变量的分布函数
用分布函数计算某些事件的概率
P{a ≤ X ≤ b} = P{X ≤ b}− P{X < a}
= F (b) − F (a − 0)
P{a < X < b} = P{X < b}− P{X ≤ a} P{a ≤ X < b} = P{X < b}− P{X < a}
= F (b − 0 ) − F (a − 0 )
设 F ( x) = P{ X ≤ x} 是随机变量 X 的分布函数,则 P{ X = a} = P{ X ≤ a} − P{ X < a} P{a < X ≤ b} = P{ X ≤ b} − P{ X ≤ a} P{ X < a} = F ( a − 0)
= F ( a ) − F ( a − 0) = F ( b) − F ( a )
随机变量的分布函数
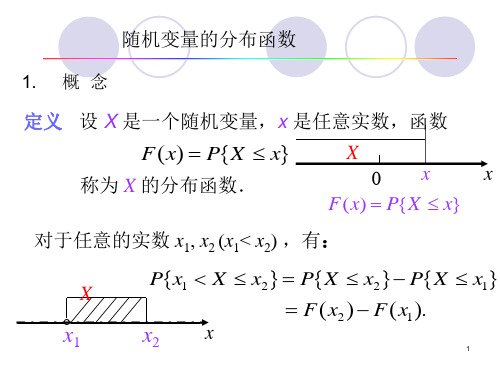
1. 概 念
定义 设 X 是一个随机变量,x 是任意实数,函数
F(x) = P{X ≤ x}
称为 X 的分布函数.
X x 0 F(x) = P{X ≤ x} x2) ,有: : X
o
P{x1 < X ≤ x2} = P{X ≤ x2}− P{X ≤ x1} = F(x2 ) − F(x1).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.4 随机变量函数的分布对离散型随机变量,我们讨论过随机变量函数的分布问题,对一般的随机变量当然也存在同样的问题。
例如,若ξ是N (2,σμ)分布的随机变量,为了解决计算中的查表问题,在中曾经引入变换η=σξa -这个新出现的随机变量η就是原来的随机变量ξ的一个函数。
现在来讨论连续型随机变量函数的分布问题,先介绍一个便于应用的定理。
定理3.1 设ξ是一个连续型随机变量,其密度函数为p (x),又y =)(x f 严格单调,其反函数)(x h 有连续导数,则=η)(ξf 也是一个连续型随机变量,且其密度函数为⎩⎨⎧<<*=其他,0|],)(|)([)('βαϕy y h y h p y (3.51) 其中α=min{)(-∞f ,)(+∞f }β=min{)(-∞f ,)(+∞f } (证明略)例3.11(略)例3.12(略)2χ—分布 我们先给出下述一个式子:p (x,y)=⎪⎩⎪⎨⎧≤>Γ-0,00,)2(212x x x ny n我们通常把以上述(3.53)式(其中n 是参数)为密度函数的分布称为是自由度为n 的2χ—分布(2χ读作“卡方”),并记作)(2n χ,它是数理统计中一个重要的分布。
(一)和的分布设),(ηξ是一个二维连续型随机变量,密度函数为p (x,y),现在来求ηξζ+=的分布,按定义为F ζ(y)= P (ζ<y)= P (ηξ+<y)如果),(ηξ表示平面上点的坐标,则P (ηξ+<y)表示点落入ηξ+= y 左边部分的概率(图略)。
由(3.37)式有F ζ(y)=⎰⎰<+yx x dxdx x x p 212121),(=dx dx x x p )),((221⎰⎰∞∞-∞∞- (3.54)如果ξ与η是独立的,由(3.48)知P ξ(x)·P η(y)是(ηξ,)的密度函数,用P ξ(x)·P η(y)代替(3.54)式中的p (x 1,x 2)便得F ζ(y) =dx dx x p x p ))()((221⎰⎰∞∞-∞∞-ηξ=dx dz x z p x p y))()((11⎰⎰∞∞-∞--ηξ=dz dx x z p x p y))()((11⎰⎰∞-∞∞--ηξ由此可得ζ的密度函数为F ζ(y)= F 'ξ(y)=dx x y p x p ⎰∞∞--)()(ηξ (3.55)由对称性还可得F ζ(y)=dx x p x y p ⎰∞∞--)()(ηξ (3.56)由(3.55)或(3.56)式给出的运算称为卷积,通常简单地记作P ζ=P ξ* P η例3.13(略)我们已经知道某些分布具有可加性,其实还有一些其它分布,也具有可加性,其中2χ—分布的可加性在数理统计中颇为重要,我们这里顺便证明这个结论。
为此,可以讨论更一般形式的一个分布—Γ分布。
如果随机变量ξ具有密度函数为p (x,y)=⎪⎩⎪⎨⎧≤>Γ--0,00,)(1x x e x xβαααβ (3.57)(其中α>0, β>0为两个常数),这时称ξ是参数为(α,β)的Γ分布的随机变量,相应的分布称作参数为(α,β)的Γ分布,并记作Γ(α,β). 例3.14(略)(二)商的分布设),(ηξ是一个二维连续型随机变量,密度函数为p (x 1,x 2),现在来求ηξζ=的分布,按照定义F ζ(y)= P (ζ<y)= P (ηζ<y) 若仍然),(ηξ把看成平面上点的坐标,则P (ηζ<y)表示点落入下图中阴影部分的概率。
(图略)利用(3.56)式,有F ζ(y)=⎰⎰<y x x dx dx x xp 2212121),(=⎰⎰><0;21212221),(x y x x dx dx xx p +⎰⎰<<0;21212221),(x y x x dx dx xx p=20121)),((2dx dx x x p yx ⎰⎰∞∞-+20121)),((2dx dx x x p yx ⎰⎰∞-∞于是ζ的密度函数为P ζ(y)=F 'ξ(y)=20222),(dx x y x p x ⎰∞–20222),(dx x y x p x ⎰∞-=⎰∞∞-dx x yx p x ),(|| (3.58)例3.16(略)F —分布 我们先给出下述一个式子:P ζ(y)=21222)()2()2()2(nm nm n m ny y m n m n n m +-+ΓΓ+Γ (3.59)我们通常把以上述(3.59)式(其中m ,n 是参数)为密度函数的分布称为是参数为m ,n 的F —分布,并记作F (n ,m ),它也是数理统计中最常用的分布之一。
引理3.1 若随机变量ξ与η相互独立,又)(x f 、)(x g 是两个连续或逐段连续的函数,则)(x f 与)(ηg 相互独立。
这个引理的结论在直觉上可以说是显然的。
因为ξ与η的取值既然是独立的,也就是互相没有牵连,那么它们的函数)(x f 、)(x g 的取值也是没有牵连的,这就是说它们是独立的。
t —分布 我们先给出下述一个式子:P ζ(y)=212)1()2(2)21(+-+Γ+Γn n y n n π (3.60)我们通常把以上述(3.60)式(其中n 是参数)为密度函数的分布称为是自由度为n 的t —分布它也是数理统计中常用的分布之一。
入分布函数时,我们已经知道描述一般随机变量的统计规律需要用分布函数F (x)=P (x <ξ),以代替离散场合用的分布列P (a =ξ),在引入独立性的定义时,也作这样的替代,这时就有下面的定义。
定义 3.5 设二维随机变量(ηξ,)的联合分布函数为F (x,y),又ξ与η的分布函数为F ξ(x)、F η(y),若对任意的(x,y)有F (x,y)= F ξ(x)·F η(y) (3.47)成立,则称随机变量ξ与η是相互独立的。
如果(ηξ,)是二维连续型随机变量,则ξ与η也都是连续型随机变量,它们的密度函数分别为P ξ(x)及P η(y)。
这时容易验证ξ与η独立的充要条件为P ξ(x)·P η(y)是(ηξ,)的密度函数 (3.48)现在来验证这一结论。
如果已知P ξ(x)·P η(y)是(ηξ,)的密度函数,就有F (x,y)=dudv v p u p xy⎰⎰∞-∞-)(*)(ηξ=dv v p du u p xy⎰⎰∞-∞-*)()(ηξ= F (x,y)= F ξ(x)·F η(y)故(3.47)式成立;反之,若已知(3.47)式成立,则F (x,y)= F ξ(x)·F η(y)=dv v p du u p xy⎰⎰∞-∞-*)()(ηξ=dudv v p u p x y⎰⎰∞-∞-)(*)(ηξ对任意的(x,y)成立,因而P ξ(x)·P η(y)是(ηξ,)的密度函数(3.48)式成立。
由此可知,要判断连续型随机变量ξ与η是否独立?只要验证P ξ(x)·P η(y)是否是(ηξ,)的密度函数就可以了。
一般说来,这是比较容易的。
例3.10 若二维随机变量(ηξ,)服从N (1a ,1a ,21σ,22σ,0)分布,问ξ与η是否独立?解 这),(ηξ时有密度函数),(y x p =])()([21212222212121σσσπσa y a x e -+--由例3.8可知P ξ(x)=21212)(121σπσa x e--P ξ(x)=22222)(221σσa y e--显然这时P ξ(x)·P η(y)= p (x,y)成立,所以ξ与η相互独立。
反之,若ξ与η独立,则必有ρ=0。
所以对二维正态随机变量N (1a ,1a ,21σ,22σ,0)来说,ρ=0是它们相互独立的充要条件。
这一节我们从一般的n 维随机变量的定义出发,而后对二维随机变量作了较多的讨论,这主要是为了叙述和学习方便的缘故。
其实,把对二维的讨论推广到n 维,并没有什么实质性的困难。
例如,对n 维随机变量的独立性,就有下述定义。
定义3.6 设n 维随机变量(1ξ,2ξ,…,n ξ)的联合分布函数为F (x 1,x 2,… ,x n ),其边际分布为F 1ξ(x 1), F 2ξ(x 2),…, F n ξ(x n ),如果对任意的(x 1,x 2,… ,x n),有F (x 1,x 2,… ,x n )= F 1ξ(x 1)·F 2ξ(x 2),…, F n ξ(x n ) (3.49)成立,则称1ξ,2ξ,…,n ξ是n 个相互独立的随机变量。
如果(1ξ,2ξ,…,n ξ)是连续型随机变量,相应的边际密度函数为p 1ξ(x 1),p 2ξ(x 2),…, p n ξ(x n ),则的等价形式为p 1ξ(x 1)·p 2ξ(x 2),…,p n ξ(x n )是(1ξ,2ξ,…,n ξ)的密度函数。
(3.50)。
