七数开立方与开N次方
12.3 立方根和开立方(教学课件)-2023-2024学年七年级数学下册同步精品课堂(沪教版)

3
x 5
知识总结
平方根与立方根的区别和联系
平方根
正数 两个,互为相反数
性
0
0
质
没有平方根
负数
表示方法
被开方数
的范围
± a
非负数
立方根
一个,为正数
0
一个,为负数
3
a
可以为任何数
典例精讲
教材第12页
例1 求下列各数的立方根:
8
(1) 1000; (2) ; (3) -0.001; (4) 0.
3
3
3
3
100 (精确到 0.001),并利用你发现的规律求
3
3
0.1 , 0.0001, 100000 的近似值.
3
0.000216 = 0.06
3
216 = 6
3
3
0.216 = 0.6
216000 = 60
总结
被开方数的小数点向左或向右移动 3n 位时立方根的
小数点就相应的向左或向右移动 n 位 (n 为正整数).
解:依次按键:
3
2ndF
显示:7,所以
依次按键: 2ndF
3
3
4
3
=
343 = 7.
3
显示:-1.1,所以
(-)
3
1
.
3
1.331 = 1.1.
3
1
=
例3 用计算器求
3
2 的近似值(精确到 0.001).
解 : 依次按键: 2ndF
显示:1.259 921 05
所以, 2 1.260.
3
A )
A.
B.-
七年级(下)数学 同步讲义 实数的概念及数的开方 (解析版)
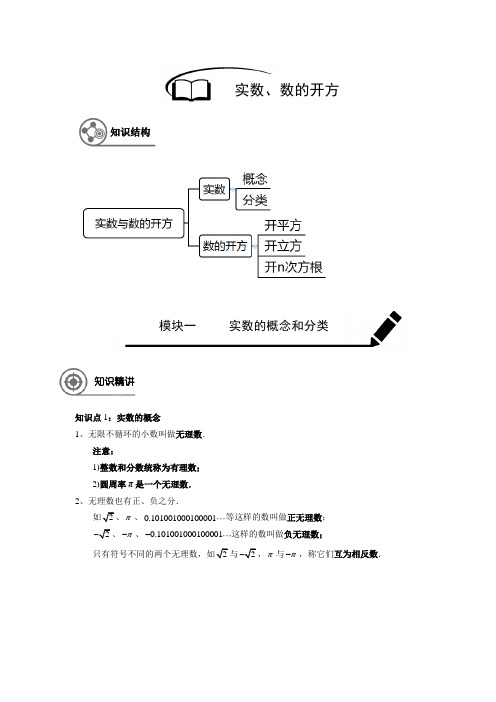
知识点1:实数的概念1、无限不循环的小数叫做无理数.注意:1)整数和分数统称为有理数; 2)圆周率π是一个无理数. 2、无理数也有正、负之分.如2、π、0.101001000100001等这样的数叫做正无理数;2-、π-、0.101001000100001-这样的数叫做负无理数;只有符号不同的两个无理数,如2与2-,π与π-,称它们互为相反数.实数、数的开方知识结构模块一 实数的概念和分类知识精讲3、有理数和无理数统称为实数. (1)按定义分类⎧⎫⎧⎪⎪⎨⎬⎨⎪⎩⎭⎪→⎩整数有理数有限小数或无限循环小数实数分数无理数无限不循环小数(2)按性质符号分类0⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正有理数正实数正无理数实数负有理数负实数负无理数【例1】 写出下列各数中的无理数:3.1415926,2π,16,.0.5,0,23-,0.1313313331…(两个1之间依次多一个3),0.2121121112.【答案】2π、0.1313313331….【解析】无限不循环小数都是无理数. 【总结】考查无理数的概念.【例2】 判断正误,在后面的括号里对的用“√”,错的记“×”表示.(1)无限小数都是无理数. ( ) (2)无理数都是无限小数.( ) (3)带根号的数都是无理数.( ) (4)不带根号的数一定不是无理数.()【答案】(1)×; (2)√; (3)×; (4)×.【解析】(1)无限不循环小数才是无理数;(2)无理数是无限不循环小数当然是无限小数; (3)开方开不尽的数是无理数;(4)π没带根号但是无理数. 【总结】考查无理数的概念及无理数与小数的关系.【例3】 a 是正无理数与a 是非负无理数这两种说法是否一样?为什么. 【答案】一样.例题解析【解析】a 是非负无理数实质上就是说a 是正无理数,因为0不是无理数. 【总结】考查无理数的分类及无理数的概念.【例4】 若a +bx =c +dx (其中a 、b 、c 、d 为有理数,x 为无理数),则a =c ,b =d ,反之, 亦成立,这种说法正确吗?说明你的理由. 【答案】略.【解析】移项得:()()a c d b x -=-, 因为非零有理数乘以无理数的结果还是无理数,而a c -是有理数(两个有理数的差仍是有理数),忧伤0d b -=,从而0a c -=, 于是有:a c b d ==,,当a c b d ==,时,等式a bx c dx +=+成立. 【总结】考查有理数、无理数的运算性质.【例5】 3为什么是无理数?请说明理由.【解析】假设3是有理数,则3能写成两个整数之比的形式:3p q=, 又因为p 、q 没有公因数可以约去,所以pq是最简分数. 把3p q=两边平方,得223p q =,即223q p =.由于23q 是3的倍数,则p 必定是3的倍数.设3p m =, 则2239q m =, 同理q 必然也是3的倍数,设3q n =,既然p 、q 都是3的倍数,它们必定有公因数3,与前面假设pq是最简分数矛盾, 故3是无理数.【总结】考查对无理数的理解及证明.模块二:数的开方知识精讲一、开平方:1、定义:求一个数a的平方根的运算叫做开平方.2、如果一个数的平方等于a,那么这个数叫做a的平方根.这个数a叫做被开方数.x=±,1的平方根是1±.如21x=,1说明:1)只有非负数才有平方根,负数没有平方根;2)平方和开平方互为逆运算.3、算术平方根:正数a的两个平方根可以用“a的正平方根(又叫算术平方根),读作“根号a”;a的负平方根,读作“负根号a”.★注意:1)一个正数有两个平方根,这两个平方根互为相反数;零的平方根是0;2=2是被开方数的根指数,平方根的根指数为2,书写上一般平方根的根指数2略写;3)一个数的平方根是它本身,则这个数是0.二、开立方:1、定义:求一个数a的立方根的运算叫做开立方.2、如果一个数的立方等于a,那么这个数叫做a的立方根号a a叫做被开方数,“3”叫做根指数.★注意:1)任意一个实数都有立方根,而且只有一个立方根;负数有立方根;2)零的立方根是0;3)一个数的立方根是它本身,则这个数是0,1和-1.三、开n次方:1、求一个数a的n次方根的运算叫做开n次方.a叫做被开方数,n叫做根指数.2、如果一个数的n次方(n是大于1的整数)等于a,那么这个数叫做a的n次方根.3、当n为奇数时,这个数为a的奇次方根;当n为偶数时,这个数为a的偶次方根.★注意:1)实数a a是任意一个数,根指数n是大于1的奇数;2)正数a”表示,负n次方根用“0n=时,在中省略n);a>,根指数n是正偶数(当23)负数的偶次方根不存在;4)零的n 次方根等于零,表示为00n =.【例6】 写出下列各数的平方根:(1)9121; (2)2(9)-.【答案】(1)311±; (2)3±. 【解析】注意要先把题中给的算式化简,再求它的平方根. 【总结】考查平方根的概念,注意平方根有两个.【例7】 写出下列各数的正平方根: (1)225;(2)9.【答案】(1)15;(2)3.【解析】(1)15; (2)93=,3的正平方根是3. 【总结】考查平方根的概念,注意对正平方根的准确理解.【例8】 下列各式是否正确,若不正确,请说明理由.(1)1的平方根是1;(2)9是2(9)-的算术平方根; (3)π-是2π-的平方根;(4)81的平方根是9±.【答案】(1)×; (2)√; (3)×; (4)×.【解析】(1)错误:1的平方根是1±;(2)正确;(3)错误:2π-是负数,没有平方根; (4)2π-错:819=,9的平方根是3±.例题解析【总结】考查平方根的基本概念,注意一定要先化简,再求平方根.【例9】写出下列各数的立方根:(1)216;(2)0;(3)1-;(4)3438-;(5)27.【解析】(1)6;(2)0;(3)1-;(4)72-;(5)3.【总结】本题主要考查立方根的概念.【例10】判断下列说法是否正确;若不正确,请说明理由:(1)一个数的偶次方根总有两个;()(2)1的奇次方根是1±;()(3)7=±;()(4)2±是16的四次方根;()(5)a的n次方根的个数只与a的正负有关.()【答案】(1)×;(2)×;(3)×;(4)√;(5)×.【解析】(1)错误:负数没有偶次方根;(2)错误:奇次方根只有一个,所以1的奇次方根是1;(37=;(4)正确;(5)错误:还与n的奇偶性有关.【总结】考查数的开方的基本概念,注意奇次方根与偶次方根的区别.【例11】写出下列各数的整数部分和小数部分:(1(2(3)9【解析】(1)因为89=,8,8;(2)因为78==77;(3)因为34=,所以596<<,所以95,小数部分为4-【总结】考查利用估算法求出无理数的整数部分和小数部分.【例12】 求值:(1 (2);(3)2; (4)2(.【解析】(1)12; (2)0.1- ; (3)4; (4)11. 【总结】考查对平方根的理解及运用.【例13】 求值:(1 (2 (3; (4【解析】(1)4; (2)35-; (3)原式54=-; (4)原式2-. 【总结】考查实数的立方根的运用.【例14】 求值:(1 (2 (3; (4【解析】(1)6 ; (2)3 ; (3)3- ; (4)2. 【总结】考查实数的奇次方根与偶次方根的计算.【例15】 求值:(1(2)(3.【解析】(1)0.5 ; (2)原式=95; (3)原式60=. 【总结】考查实数的立方根运算.【例16】 小明的房间面积为17.62m ,房间的地面恰好由110块大小相同的正方形地砖铺成,问:每块地砖的边长是多少? 【答案】0.4m .【解析】设每块地砖的边长是x 米,则有:211017.6x =,化简得20.16x =,解得:0.4x = 即每块地砖的边长是0.4m .【总结】考查实数的运算在实际问题中的运用.【例17】 已知2a -1的平方根是3±,3a +b -1的算术平方根是4 【答案】3.【解析】由题意知:219a -=,3116a b +-=,即210a =,173b a =-解得:5a =,2b =,所以2549a b +=+=3=. 【总结】本题主要考查实数的平方根与算术平方根的区别,以及代数式的值.【例18】 若a 的平方根恰好是方程3x +2y =2的一组解,求x y a a +的值.【答案】125716()1616或.【解析】由题意,因为a 的两个平方根是相反数,那么y x =-,则有:32322x y x x +=-=,即2x =,2y =-.那么由题意可得:4a =,所以22125744161616x y a a -+=+=+=. 【总结】本题主要考查实数的平方根与求代数式的值.【例19】 3,3(43)8x y +=-,求2()n x y +的值. 【答案】1.【解析】由题意可得:49432x y x y -=⎧⎨+=-⎩, 解得:12x y =⎧⎨=-⎩,所以222()(12)(1)1n n n x y +=-=-=.【总结】本题考查实数的开方以及二元一次方程组的解法,学生忘记解方程组的情况下,老师可以略微拓展复习一下二元一次方程组的解法哦.【例20】用“>”把下列各式连接起来:=,-12-23【总结】本题考查实数的大小比较,注意先化简,再比较大小.【例21】 1.732 5.477≈,利用以上结果,求下列各式的近似值.(1≈_______;(2____________;(3≈_________;(4≈______________;(5___________;(6≈_____________.【答案】略.【解析】(1 1.7321017.32⨯=;(2 5.4771054.77≈⨯=;(3 1.732100173.2⨯=;(4 5.4770.10.5477≈⨯=;(5 1.7320.10.1732⨯=;(6 5.4770.010.05477≈⨯=.【总结】本题考查实数的运算,注意每题之间的联系,类比推理.【例22】填写下表,并回答问题:a…0.000001 0.001 1 1000 1000000 …….3a……(1)数a与它的立方根3a的小数点的移动有何规律?(2)根据这个规律,若已知33,,求a的值.==a0.005250.1738 1.738【解析】(1)由题可知,被开方数a的小数点每向右或向左移动三位,立方根3a的小数点相应地向右或向左移动一位;(2)由(1)总结的规律可知: 5.25a=.【总结】本题考查实数的开方与被开方数之间的关系,注意引导学生仔细分析表格.【例23】阅读下面材料并完成填空:你能比较两个数20162017和20172016的大小吗?为了解决这个问题先把问题一般化,要比较n n+1和(n+1)n的大小(的整数),先从分析n=1,=2,=3,……这些简单的情况入手,从中发现规律,经过归纳,猜想出结论.(1)通过计算,比较下列①—⑦各组中两个数的大小(在横线上填“>、=、<”号①12______21;②23______32;③34______43;④45______54;⑤56______65;⑥67______76;⑦78______87.(2)对第(1)小题的结果进行归纳,猜想出n n+1和(n+1)n的大小关系: ______(3)根据上面的归纳结果猜想得到的一般结论是:20162017_____20172016.【答案】(1)①<;②<;③>;④>;⑤>;⑥>;⑦>:(2)当n =1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n;(3)>.【解析】(1)①12 <21;②23<32;③34>43;④45>54;⑤56>65;⑥67>76;⑦78>87;(2)当n=1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n;(3)根据第(2)小题的结论可知,20162017>20172016.【总结】本题考查实数的运算规律,注意观察计算后的结果,总结出规律。
2021人教版七年级下册 实数 立方根 讲义(解析版)

实数立方根知识讲解一、立方根的定义如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果3x a=,那么x叫做a的立方根.求一个数的立方根的运算,叫做开立方.补充:一个数aa是被开方数,3是根指数. 开立方和立方互为逆运算.二、立方根的特征立方根的特征:正数的立方根是正数,负数的立方根是负数,0的立方根是0.补充:任何数都有立方根,一个数的立方根有且只有一个,并且它的符号与这个非零数的符号相同. 两个互为相反数的数的立方根也互为相反数.三、立方根的性质==a=;3a补充:第一个公式可以将求负数的立方根的问题转化为求正数的立方根的问题.四、立方根小数点位数移动规律被开方数的小数点向右或者向左移动3位,它的立方根的小数点就相应地向右或者向左移动1位.0.060.6,660.五、平方根与立方根的联系典例讲解例1、下列结论正确的是( )A .64的立方根是±4B .12-是16-的立方根 C .立方根等于本身的数只有0和1D=【答案】D ;【解析】64的立方根是4;12-是18-的立方根;立方根等于本身的数只有0和±1. 课堂巩固1.下列说法正确的是( )A .一个数的立方根有两个B .一个非零数与它的立方根同号C .若一个数有立方根,则它就有平方根D .一个数的立方根是非负数 【答案】B ;提示:任何数都有立方根,但是负数没有平方根.2.下列说法正确的是( ) A .﹣4的立方是64 B . 0.1的立方根是0.001 C . 4的算术平方根是16 D .9的平方根是±3【答案】D.例2.(1)下列运算中错误的有()=4±4=4=-4=;⑤4=A .1个B .2个C .3个D .4个【答案】C 【详解】44=4=,④不符合题意,⑤2=±,⑤符合题意,(2)64的立方根是() A .4 B .8C .8±D .2【答案】A【详解】∵4的立方是64,∴64的立方根是4课堂巩固1.求下列各式的值: (1)327102-- (2)3235411+⨯ (3)336418-⋅ (4(5)10033)1(412)2(-+÷-- 【答案】解:(1) (2(3)43===91=241=2⎛⎫⨯- ⎪⎝⎭-(4)=331=1-++(5)3=21247=1=33÷++ 2的平方根为_____. 【答案】±2【详解】∵4的立方等于64,∴64的立方根等于4.4的平方根是±2,故答案为±2.例3比计较下列各数的大小(1(2)与-3.4 (343【答案】(12)<-3.4 (3<43【详解】(1)32=82<=>>(2)342 3.476 3.4, 3.4≈><-(3)()3334646442=2=,2,327273⎛⎫<< ⎪⎝⎭, 课堂巩固1.估算31的立方根在两个整数之间. 【答案】4和52.比较22<<3.比较【答案】< 【答案】例4求下列各式中x 的值(1)()318x -=(2)8(x -1)3=-1258(3)33388x -= .【答案】(1)3x =; (2)x =-14;(2)x=3.【详解】(1)()318x -=;12x -=;3x =;(2)()3125164x -=-;514x -=-;514x =-;14x =- (3)x3﹣24=3;x3=27;∴x =3 课堂巩固1.求满足下列条件的x 的值:(1)()3231250x -+=(2)32(1)540x --=(3)(x ﹣1)3=﹣125.(4)2(x ﹣1)3+16=0 (5)327640x +=(6)12(x+3)3=4【答案】(1)1x =-;(2)x=4;(3)x=﹣4;(4)x =﹣1;(5)43x =-;(6)x =﹣1.【详解】 (1)∵()3231250x -+=,∴()323125x -=-,∴235x -=-;解得:x =−1.(2)32(1)540x --=;32(1)=54x -;3(1)=27x -;1=3x -;=4x .(3)x ﹣1=﹣5,x=﹣4.(4)2(x ﹣1)3+16=0;则(x ﹣1)3=﹣8;故x ﹣1=﹣2;解得:x =﹣1.(5)327640x +=;32764x =-;364x =-;36427x =-;43x =- (6)方程的两边都乘以2,得(x+3)3=8,∴x+3=2.∴x =﹣1.例5 1.已知x+122x+y﹣6的立方根是2.(1)求x,y的值;(2)求3xy的平方根.【答案】(1)x=1,y=12;(2)±6.【详解】(1)∵x+122x+y﹣6的立方根是2.∴x+12=2=13,2x+y﹣6=23=8,∴x=1,y=12(2)解:当x=1,y=12时,3xy=3×1×12=36,∵36的平方根是±6,∴3xy的平方根±6.2.已知2a-1的平方根是±3,3a+b-9的立方根是2,c整数部分,求a+b+c的平方根.【答案】±3【详解】解:根据题意,可得2a﹣1=9,3a+b﹣9=8;故a=5,b=2;又∵2<3,∴c=2,∴a+b+c=5+2+2=9,∴9的平方根为±3.点睛:此题主要考查了平方根、立方根、算术平方根的定义及无理数的估算能力,掌握二次根式的基本运算技能,灵活应用.“夹逼法”是估算的一般方法,也是常用方法.课堂巩固12的平方根是a ,﹣125的立方根是b ,则a ﹣b 的值是( ) A .0或10 B .0或﹣10 C .±10 D .0【答案】A【详解】2=25,∴25的平方根是±5,﹣125的立方根是﹣5,∴a =±5,b =﹣5,当a =5时,原式=5﹣(﹣5)=10,当a =﹣5时,原式=﹣5﹣(﹣5)=0, 20=,则m+n=________. 【答案】10+=;∴37340m-+n +=;∴1m+n= 【点睛】立方根的值互为相反数,被开方数互为相反数.3.若x y +是4的平方根,x y -的立方根是2-,则22x y -=___________ 【答案】16或16-【详解】x y +是4的平方根,2x y ∴+=或2,x y +=-x y -的立方根是2-,∴8,x y -=-当2,8x y x y +=⎧⎨-=-⎩22()()16,x y x y x y ∴-=+-=-当2,8x y x y +=-⎧⎨-=-⎩22()()16,x y x y x y ∴-=+-=综上:2216.x y -=±故答案为:16或16-.4.已知一个数的平方根是3a+1和a+11,求这个数的立方根是______. 【答案】4【详解】由已知得,3a+1+a+11=0,解得a=-3,所以3a+1=-8,a+11=8,所以,这个数是64,它的立方根是4.故答案是:4. 5.已知某正数的两个平方根分别是a+3和5﹣3a,(1)求这个正数;(2)若b的立方根是2,求b﹣a的算术平方根.【答案】(1)49;(2)2.【详解】(1)根据题意知a+3+5﹣3a=0,解得:a=4,所以这个数为(a+3)2=72=49;(2)根据题意知b=8=2.例6据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙.你知道华罗庚是怎样计算的吗?请按照下面的问题试一试:(1)由33==__________位数;101000,1001000000(2)由19683 个位数是3________________;(3)如果划去19683 后面的三位数683 得到数19 ,而33==___________;28,327(4)用上述方法确定110592 的立方根是_______________.【答案】两7248【分析】(1)由19683大于1000而小于1000000,即可确定59319的立方根是2位数;(2)根据一个数的立方的个位数就是这个数的个位数的立方的个位数,据此即可确定;,即可确定答案;(3)运用数立方的计算方法计算即可;(4)首先根据一个数的立方的个位数就是这个数的个位数的立方的个位数确定个位数,然再确定十位数即可解答.【详解】解:(1)∵1000<19683<1000000,∴是两位数;故答案为:两;(2)∵一个数的立方的个位数就是这个数的个位数的立方的个位数7;故答案为7;(3)∵8<19<27,∴的十位上的数是2,故答案为2;(4)∵观察发现:只有8的立方的个位数为2为8又∵64<110<1254;故答案为48.【点睛】当被开方数的小数点向右或向左每移动3位,立方根的小数点就向右或向左移动一位课堂巩固1________.【答案】7.94=10×0.794=7.94.故答案为:7.94.2≈≈≈________________1.507【答案】0.06993≈≈≈0.06993,1.507故答案为:0.06993.3.观察下列计算过程,猜想立方根.31=1 32=8 33=27 34=64 35=125 36=216 37=343 38=512 39=729(1)小明是这样试求出19683的立方根的,先估计19683的立方根的个位数, 猜想它的个位数为, 又由320<19000< 330,猜想19683的立方根十位数为,验证得19683的立方根是 . (2)请你根据(1)中小明的方法,完成如下填空:= = .【答案】(1)7,2,27;(2)49,-72,0.81【详解】(1)先估计19683的立方根的个位数,猜想它的个位数为7,又由203<19000<303,猜想19683的立方根十位数为2,验证得19683的立方根是27(2)①估计117649的立方根的个位数为9,又由403<117649<503=49;②估计373248的立方根的个位数为2,又由603<373248<703;③估计0.531441的立方根的个位数为,又由0.83<0.531441<0.93=0.81 .4.阅读下列材料:33=331059319100,<<39729,<<,则3594==________.39【答案】54【详解】33=33<<3464,10157464100,=,故答案为54.51576<<54课后提升一、单选题1.下列说法:①负数和0没有平方根;②所有的实数都存在立方根;③正数的绝对值等于它本身;④相反数等于本身的数有无数个.正确的个数是()A.0 B.1 C.2 D.3【答案】C【详解】①0有平方根,故错误;②所有的实数都存在立方根,故正确;③正数的绝对值等于它本身,故正确;④相反数等于本身的数有1个,故错误;2.下列结论正确的是()A .1535-÷=B .3=±C 2=-D .()()2233-=+ 【答案】D3.下列说法错误的是( )A .2±B .64的算术平方根是4CD 0≥,则x =1【答案】B二、填空题4.计算()03π-=__________. 【答案】2-5.若x <0____________.【答案】0【详解】∵x <00x x =-+=,故答案为:0.635.12=0.3512=-,则x =_____________.【答案】-0.0433【详解】从35.12变为-0.3512,缩小了100倍,且添加了“-” ∴根据规律,三次根式内的式子应该缩小1000000倍,且添加“-”7.已知368.8=4.098,,则______________.【答案】19.028 1.463≈ 4.626≈0.5981≈.289≈,若46.26≈,则x =_______ 5.981≈-,则y =_______.【答案】2140-214三、解答题9.已知2a -1的平方根是±3,b -1的立方根是2,求a-b 的值.【答案】4a b -=-.【详解】因为9的平方根是3±,8的立方根是2所以21918a b -=⎧⎨-=⎩;解得59a b =⎧⎨=⎩;则594a b -=-=-. 10.已知 2a ﹣1 的平方根是±3,b ﹣3 的立方根是 2的值.【答案】6.【详解】解:∵2a ﹣1的平方根是±3,∴2a ﹣1=9,∴a=5,∵b ﹣3的立方根是2,∴b ﹣3=8,∴b=11.故答案为:6.11.已知2a -1的算术平方根是3,3a +b +4的立方根是2,求a -b 的平方根.【答案】a -b 的平方根是±4.【详解】∵2a -1的算术平方根是3,3a +b +4的立方根是2,∴2a -1=9,3a +b +4=8,解得a =5,b =-11,∴a -b =16,∴a -b 的平方根是±4.12.解方程(1)2(x-1)2= 128 (2)(x-4)3 = -216(3)225640-=x ;(4)3343(3)270x ++=(5)24810x -=(6)()3164x -= 【答案】(1)x=9或x=-7; ( 2 ) x= -2;(3)85x =±;(4)337x =-;(5)92x =或92x =-;(6)5x = 【详解】(1)22(1)1?28x -=,2(1)64x -=,18x -=±, 18x -=或18x -=-,9x =或7x =-;(2)3(4)? 216x -=-, 4? 6x -=-, 2x =-. (3)225640-=x ;解:225=64x ,264=25x ,85x =±; (4)3343(3)270x ++=.解: 3343(3)27x +=-,327(3)343x -+=,337x +=-,337x =-. (5)解:2481x =;2814x =;解得92x =或92x =- (6)解:()3164x -=;14x -=;解得5x = 13a b的值. 【答案】32=0,2a -1=3b -1, 2a =3b ,∴a b =32. 14是48的立方根,求1mn +的平方根.【答案】±4【详解】由题意得24228n m m -+=⎧⎨+=⎩解得:35m n =⎧⎨=⎩∴1mn +=3×5+1=16 ∴1mn +的平方根是±4;故答案为:±415.(1)已知,图1正方体的棱长为a ,体积是50,求正方体的棱长a ;(2)已知,图2是由16个边长为1的小正方形组成的大正方形,图中阴影部分也是一个正方形,求阴影部分正方形的边长b .【答案】(1(2【详解】解:(1)350a =,a ∴=(2)由題意可知,大正方形的面积是由阴影部分的面积和四个真角三角形的面积组成的,4416S =⨯=大正方形,133122S =⨯⨯=小三角形, ∴=4S S S -阴影大正方形小三角形23=16410=2b -⨯=,b ∴= 16.如图1,这是由8个同样大小的立方体组成的魔方,体积为64.(1)求出这个魔方的棱长.(2)图中阴影部分是一个正方形ABCD ,求出阴影部分的面积及其边长.(3)把正方形ABCD 放到数轴上,如图2,使得A 与1-重合,点E 与1重合,点F 与点D 关于E 点对称,那么D 在数轴上表示的数为__________;点F 在数轴上表示的数为__________.【答案】(1)4;(2)8,(3)1--,3+.【详解】(14=,∴这个魔方棱长为4.(2)∵魔方棱长为4,∴小立方体棱长为2,∴阴影部分面积为:1⨯⨯⨯==8,边长是22482(3)D在数轴上表示的数是1--F表示为++=+123。
人教版七年级下册数学6.2 立 方 根课件

3a3
.
解:(1) 3 64 3 64 -4 ;
(2) 3 0.064 3 0.43 0.4 ;
(3) 3 27 3 3 3 3 ; 125 5 5
(4) 3 a 3 a.
提示:求一个负数的立方根,可以先求出这个负 数绝对值的立方根,然后再取它的相反数.
由于一个数的立方根可能是无限不循环小数,所以 我们可以利用计算器求一个数的立方根或它的近似值. 例4 用计算器求下列各数的立方根:343,-1.331.
如∵ (3)2 9 , ∴ ﹢3 是9的算术平方根,
即 9 3
式子读作“9的算术平方根等于3” 或“根号9等于3” 规定:0的算术平方根是0
填空:
求平方
1 1
1
2 2
4
3
9
3
平方 互逆 运算
开平方
求平方根
1
1 1
4
2 2
9
3
3
求一个数a的平方根的运算,叫做开平方.
你能类比平方根的定义给出立方根的定义吗?
立方根的估算 50的立方根记作
3 50 .
问题:3 50 有多大呢?
因为 33 27 , 43 64
所以
3
‗‗‗‗3‗.6‗8
3
50
‗3‗.6‗9‗4‗‗‗‗
因为 3.63 46.656 , 3.73 50.653
所以 ‗‗‗3‗.‗6‗3‗.‗68‗ 3 50 3‗.6‗39‗.7‗‗‗‗‗
你能看出正数,0,负数的立方根各有什么特点?
8的立方根是 2
0.125的立方根是
1 2
-8的立方根是 -2 0的立方根是 0
归纳:
一个数的立方根只有一个; 正数的立方根是正数; 零的立方根是零; 负数的立方根是负数。
(完整版)七年级下第六章数学知识点(人教版)

第六章实数本章重点讲解:一个对应(实数与数轴上的点一一对应),两种表示,两个运算,四个概念(平方根、算术平方根、立方根和实数)1、算术平方根⑴定义:一般地,如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根。
⑵表示:a的算术平方根用符号表示为a,读作“根号a”,a叫做被开方数。
规定:0的算术平方根是0。
注:算术平方根具有双重非负性,即a≥0,a≥0。
2、平方根⑴定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,也就是说,若x²= a,则x叫做a的平方根。
⑵表示:一个非负数a的平方根用符号表示为“±a”。
⑶性质:正数的平方根有两个,它们互为相反数;0的平方根是0;负数没有平方根。
3、开平方是指求一个非负数的平方根的运算注:开平方与平方是互逆运算,可以通过平方运算来求一个数的平方根或算术平方根,以及检验一个数是不是另一个数的平方根或算术平方根。
4、平方根的相关结论⑴当被开方数扩大(或缩小)n²倍,它的算术平方根相应地扩大(或缩小)n倍(n≥0)。
⑵平方根和算术平方根与被开方数之间的关系:a(a≥0)①(a)²= a(a≥0);②a=∣a∣=-a(a<0)a之间,即当⑶若一个非负数a介于另外两个非负数a1、a2之间,它的算术平方根介于a1、2a。
利用这个结论我们可以估算一个非负数的算术平方根0≤a1<a<a2时,则0≤1a<a<2的大致范围。
5、立方根⑴定义:如果一个数的立方等于a,那么这个数叫做a的立方根,也就是说,若x³=a,则x叫做a的立方根。
⑵表示:一个数a的立方根用符号表示为“3a”,其中“3”叫做根指数,不能省略。
3a读作“三次根号a”。
⑶性质:正数的立方根为正数;负数的立方根为负数;0的立方根为0.6、开立方是指求一个数的立方根的运算注:开立方与立方是互逆运算,可以通过立方运算来求一个数的立方根,以及检验一个数是不是另一个数的立方根。
沪教版初中七年级数学第一学期(试用本):n 次方根_课件1

2. 平方根的特征:
3. 立方根的特征:
在乘方运算中有:
平方,它的逆运算—— 开平方 。
立方,它的逆运算—— 开立方 。
n次方,它也有逆运算—— 开n次方 。
开平方——求一个数a的平方根的运算 。 开立方—— 求一个数a的立方根的运算 。
开n次方——求一个数a的n次方根的运算 。 下面我们来研究n次方根 及开n次方。
n
an a
a (a 0) a a a (a 0)
n
n
求值 ( 1) ( 3)
3
(8) 3 ( 3 )
如果x 81, 那么x就叫做81的四次方根 ________, 5 如果x 243, 五次方根 , 那么x就叫做243的________ …… 如果一个数(x)的n次方(n是大于1的整数)等
4
于a,那么这个数(x)叫做a的n次方根。 当n为奇数时,这个数(x)偶次方根。 有时 n次方根简称“方根”, 求一个数 a的n次方根的运算叫做 开n次方,a叫做被开方数,n叫 开n次方简称“开方”。 做根指数。
例题:
32 (1)求 的5次方根; 243
(2)求1024的10次方根;
(3)求 8 的6次方根.
2
32 2 2 5 5 . 解:(1) 243 3 3 10 10 10 (2) 1024 2 2.
5
(3)
6
6 6 6 8 64 2 2.
n次方根
1. 求下列各式的值:
1
10 -0.6 100 _____; 2 0.36 _____;
3
3
2 2 2 3 4 3 5 5 3 _____; 6 27 _____;
沪教版(五四制)七年级数学下册 12.2数的开方同步讲义(带答案)

——数的开方(★)1.了解平方根、算术平方根、立方根的概念,会用根号表示;2.了解平方与开平方、立方与开立方互为逆运算,会用平方、立方的运算求某些数的平方根与立方根,会用计算器求一个非负数的算术平方根及任意一个数的立方根;3.估计无理数的大小,培养估算能力,会进行简单的实数运算;4.能灵活运用平方根、绝对值的性质.每个模块要标准课堂用时建议,共计40分钟。
建议3分钟一、复习引入1.我们将要学习的第12章叫:数的开方,那什么叫“数的开方”呢?我们已学过哪些数的运算?(加、减、乘、除、乘方5种)2.你能写出这些运算的符号吗?请举例说明。
如一个正方形的边长是5米,它的面积是多少?其运算是什么运算? (面积25平方米,运算是乘方运算)3.加法与减法这两种运算之间有什么关系?乘法与除法之间呢?(均为互逆运算)二、问题引入采用课堂提问的方式,提问内容涵盖本节课的基本知识点。
建议7分钟1.平方根、算数平方根的概念,以及它们之间的区别和联系(1)平方根的概念:如果一个数的平方等于a,那么这个数叫做a的平方根。
一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
(2)算术平方根概念:正数a的正的平方根,叫做a的算术平方根,记作a正数a的正的平方根就是a的算术平方根;正数a的平方根有两个,并且互为相反数,而正数a的算术平方根只有一个。
2.开平方和开平方的方法a≥的平方根的运算,叫做开平方。
(1)开平方:求一个数a()0开平方运算是已知指数和幂求底数。
平方与开平方互为逆运算。
7a是非负数;a是非负数。
3求平方根的方法:根据平方根的定义,可以利用平方来检验或寻找一个数的平方根3.立方根和开立方(1)任何数(正数、负数或零)的立方根如果存在的话,必定只有一个。
(2)数a的立方根,记作3a,读作“三次根号a”。
a称为被开方数,3称为根指数。
(3)求一个数的立方根的运算,叫做开立方。
4.n次方根和开n次方(1)如果一个数的n次方(n是大于1的整数)等于a,那么这个数就叫做a的n次方根. (2)求一个数a的n次方根的运算叫做把a开n次方,a叫做被开方数,n叫做根指数.一个数a的n次方根可以分为奇次方根和偶次方根两类:当a为奇数时:一个数a的奇次方根只有一个,记作a正数的奇次方根是一个正数;负数的奇次方根是一个负数;零的奇次方根是零.当n为偶数时:正数a的偶次方根有两个,它们互为相反数,记作a。
浙教版数学七年级上册立方根课件

求下列各数的立方根: (6)∵10³=10³
正数有立方根吗?如果有,有几个。
负数呢?
零呢? 从上面的例1可知:一个正数有一个正的立 方根;一个负数有一个负的立方根,零的立方根 是零。
1、做一做: (3 8 )3 ____8____ (3 27 )3 ___-__2_7___ (3 0 )3 _____0_____ (3 2 )3 _____2_____
2、做一做:
3 23 2
3 ( 3)3 4
3 (2)3 -2
3 (0.1)3 -0.1
a
3、做一做:
(1)3 8 _-__2_,3 8 __-_2__; (2)3 27 _-__3_,3 27 _-__3_; (3)3 0.001 _-__0_.1_,3 0.0001 _-_0_._1。
求一个数的立方根(三次方根)的运算,叫 做开立方,开立方运算的结果就是立方根。
因为开立方与立方互为逆运算。
所以我们可以运用立方运算来求一个数的 立方根。
例1:求下列各数的立方根。 (1)-27; (2)27; (3)-0.216;
(4)0;
(5) 8 125
解: ∵ (3)3 27
3
∴ 27 3
请你仿照上面的例子完成其余几个小题。
例1:求下列各数的立方根。 (1)-27; (2)27; (3)-0.216;
(4)0;
(2)∵3³=27
(5) 8 125
(4)∵0³=0
(3)∵(-0.6)³=-0.216
求下列各数的立方根:
解:(1)∵(-2)³=-8
(2)∵2³=8
求下列各数的立方根: (4)∵0.6³=0.216
(2)3 0.001 + 0.01
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题 开立方与开N 次方
【新知展望】
【开立方】
1、如果一个数的立方等于a ,那么这个数叫做a 的立方根,用“3a ”表示,读作“三次根号a”,
3
a 中的a 叫做被开方数,“3”叫做根指数;求一个数a 的立方根的运算叫做开立方。
2、正数的立方是一个正数,负数的立方是一个负数,零的立方等于零,所以正数的立方根是一个正数,负数的立方根是一个负数,零的立方根是零。
3、任意一个数都有立方根,而且只有一个立方根
4、
3
a =,a =
例1、求下列各数的立方根 (1)1000- (2)
125
64
(3)0.008 (4)0 (5)49的平方根
练习1、(1)27的立方根是_______________;8-的立方根是_______________。
(2)125
1
-
的立方根是____________;7-的立方根是_______________。
(3)27-的立方根的平方的平方根是______________________________。
(4)|64
1
|-的立方根是____________________。
(5)____________________是9
1
的平方根,又是_______________的立方根。
例2、求值
(1)336)(- (2)3512 (3)3610- (4)334- (5)38
3
3
练习2、(1;;。
(2,=-33)7(____________=_____________。
(3)使33a a --=-成立的条件是______________________________。
练习3、求下列各式中的x
(1)273=x (2)0183=-x (3)125)1(3=-x (4)016)2(23=++x
练习4、如果3200a 是一个整数,那么最大负整数a 是多少?
练习5、 若23253-=+x ,求24+x 的平方根
【开n 次方】
1、如果一个数的n 次方(n 是大于1的整数)等于a ,那么这个数叫做a 的n 次方根,当n 为奇数时,这个数为a 的奇次方根;当n 为偶数时,这个数为a 的偶次方根;求一个数a 的n 次方根的运算叫做开n 次方,a 叫做被开方数,n 叫做根指数。
2、实数a 的几次方根有且只有一个,用“n a ”表示,其中被开方数a 是任意一个实数,根指数n 是大于1的奇数;“n a ”读作“n 次根号a ”
3、正数a 的偶次方根有两个,它们互为相反数,正n 次方根用“n a ”表示;负n 次方根 用
“n a -”表示,其中被开方数0>a ,根指数n 是正偶数(当n =2时,在n a ±中省略n ) 4、负数的偶次方根不存在
5、零的n 次方根等于零,表示为00=n
例3、下列方根中,哪些有意义?哪些没有意义?如果有意义,请用符号表示这些方根并求出结果。
(1)1的五次方根; (2)1-的五次方根;
(3)16的四次方根; (4)16-的四次方根;
(5)64的六次方根; (6)32-的五次方根。
例4、求下列各式的值
(1)3125-; (2)4625; (3)
64
1
的6次方根 (4)1010)12(-
练习6、填空
(1)81的4次方根是_________________;64-的3次方根是__________________。
(2)001.0-的立方根是______________;101)1(-的7次方根是________________。
(3)0的4次方根是__________________;1-的9次方根是____________________。
(4)243-的5次方根是___________________。
(5)一个数的平方是16,那么这个数的5次方根是_____________________________。
(6)()=-553___________________,()=-363_____________________。
例5、计算
(1)63641+- (2)34
27
8
161+
-
练习7、计算 (1)()
5
2
322+-
(2)5332
1
008.0-
-
(3)43381
1
)3(-- (4)3
3512
127+-
例6、计算
(1)7
31271⎪
⎭
⎫ ⎝⎛⎪⎭⎫ ⎝⎛-的5次方根; (2)n
n 22)6(-(n 是大于1的整数)
练习8、计算
(1)()2
21.1-的4次方根; (2)1212)17(++-n n (n 是大于1的整数)
例7、当x 为何值时下列各式有意义?
(1 (2 (3 (4
练习9、x 为何值时,下列各式有意义:
(1 (2)641x - (3)32x - (4)3
)1(x
x -
练习10、解答题
(1)已知0|6862|1634=++-y x ,且x x -=||,求||y x +的值
(2)当x 为何值时,x x -=-1)1(2; 当k 4k =-?
(3)当0<a 时,化简:66333||2a a a ++
【巩固练习】
一、判断
(1)互为相反数的两个数的立方根也互为相反数
( ) (2)只有零的立方根是它本身
( ) (3)8的立方根是2±
( ) 二、选择题
1.下列说法中,正确的是 ( ) A .1的任何次方根都是1; B .0的任何次方根都是0; C .负数没有方根; D .正数的方根互为相反数; 2.下列说法错误的是 ( ) A .当n 为奇数时,实数的n 次方根有且仅有一个; B .当n 是自然数时,n a 的n 次方根为a ; C .奇次方根与偶次方根相等的数一定是0;
D .当n <0时,—n 的四次方根为3.下面四题中,做对的是 ( )
A .2
21
33a
a -=; B =C .2
1
2a a -⎛⎫=- ⎪⎝⎭
;D 2==-
4)0a ≥可化简为 ( )
A .3
2a ; B .1
8a ; C .3
4a ; D .1
6a
5.若11
222a a -+=,则1a a -+的值是 ( ) A .—2; B .2; C .4; D .0
6.111
324a a a ⋅⋅可化为 ( )
A .1
24a ; B .7
12a ; C .13
24a D .
7.一个数的立方根与这个数的平方根相等,则这个数是 ( )
A .0
B .1
C .0和1
D .0和-1
81a =-,那么a 的取值范围是 ( ) A .1a ≤ B .1a ≤- C .1a ≥ D .一切实数 二、填空题:
1.16的四次方根__________;64的六次方根__________;—343的五次方根___________。
2.正数a 有______个偶次方根,记作_________;正数a 有_______个奇次方根,记作_______; 0的偶次方根_______;0的奇次方根_______。
3.()0a a -<的六次方根__________________。
4.
14
0.0064=___________;12
12149-
⎛⎫ ⎪
⎝⎭
=____________。
53
n =,则n=_________
2x =,则x =__________。
6.计算:2的立方根是__________。
7.已知0x =,则x y 的立方根是______________,。
8.若164=x ,则x = ;若813=n ,则n = 。
9、当x = 时,13-x 有意义;当x = 时,325+x 有意义。
10、若
3x x =,则x = ;若x x -=2,则x 。
三、简答题
1.求下列各式的值:
(1 (2 (3 (4 (5)
3
8
3
3-
2.(1)已知228x =,求x 的5次方根; (2)求()2
16-的8次方根。
3.把下列各数写成分数指数幂的形式:
(1
(2)
(3
(4
(5
(6
四、解答题
1互为相反数,求代数式12x
y
+的值.
24=,且2(21)0y x -+=,求x y z ++的值.
3.已知:2x -的平方根是±2, 27x y ++的立方根是3,求22
x y +的平方根.
【拓展练习】
1.将三个数1
1
1
3242,3,5按从大到小的顺序排列。
2.若已知a b A +=3a +的算术平方根,2a b B -=2b -的立方根,求A B -的平方根。
