4多组分体系热力学
第4章 多组分热力学

前面所讨论的是:单组分单相(两相)系统或多 组分组成恒定的系统。 但常见系统绝大部分是:多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外,还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为:单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ,单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变,某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言,本身是强度量;
3 偏摩尔量与浓度有关,与系统的总量无关。
4 偏摩尔量 X B ( nX,B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下,于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积:
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B
物理化学:第4章_多组分系统热力学_
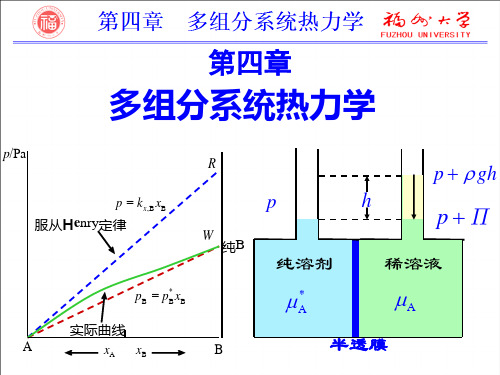
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
第4章 多组分系统热力学

第四章多组分体系热力学一、选择题1. 在298K时,A和B两种气体单独溶解在某一溶剂中,均遵守亨利定律,亨利常数分别为kА和k B,且知kА> k B,则当A和B的平衡压力相同时,在一定量的该溶剂中所溶解的关系为( ) (A) A 的量大于 B 的量;(B) A 的量小于 B 的量;(C) A 的量等于 B 的量;(D) A 的量与 B 的量无法比较。
2. 在恒温抽空的玻璃罩中封入二杯液面相同的糖水 (A) 和纯水 (B)。
经历若干时间后,二杯液面的高度将是:( )(A) A 杯高于 B 杯; (B) A 杯等于 B 杯; (C) A 杯低于 B 杯;(D) 视温度而定。
3. 在温度T时,纯液体A的饱和蒸气压为P A*,化学势为μA*,并且已知在P⊖压力下的凝固点为T f*,当A 中溶入少量与A不形成固态溶液的溶质而形成为稀溶液时,上述三物理量分别为P、μA、T f则( ) (A) P < P,μA*<μA ,T f*< T f(B) P A*> P A ,μA*<μA ,T f*< T f(C) P < P,μA*<μA ,T f*> T f(D) P A*> P A ,μA*>μA , T f*> T f4.已知在 373K 时液体A 的饱和蒸气压为66662Pa,液体B的饱和蒸气压为1.01325×105 Pa,设 A 和 B 构成理想液体混合物,则当A在溶液中的物质的量分数为0.5 时,气相 A 的物质的量分数应为:( )(A) 0.200 (B) 0.300 (C) 0.397 (D) 0.6035. 对于理想液体混合物,下列偏微商小于零的是:(A) [∂(△mix F m)/ ∂T]p(B) [∂(△mix S m)/ ∂T]p(C) [∂ (△mix G m)/T]/ ∂T]p(D) [∂ (△mix G m)/ ∂P]T6. 假设A、B 二组分混合可以形成理想液体混合物,则下列叙述中不正确的是:( )(A)A、B 分子之间的作用力很微弱;(B) A、B 都遵守拉乌尔定律;(C) 液体混合物的蒸气压介于A、B 的蒸气压之间;(D) 可以用重复蒸馏的方法使A、B 完全分离。
物理化学4 多组分体系热力学 1

几点说明
(1)偏摩尔量只对体系中某组分才具有的,对整体而 言无所谓偏摩尔量的概念; (2)只有体系的广度性质才有偏摩尔量(质量除外) ; (3)偏摩尔量本身是强度性质; (4)注意右下角标的条件; (5)任何偏摩尔量都是T、p、组成的函数; (6)纯物质的偏摩尔量就是摩尔量; (7)偏摩尔量可能是负值。 (8)偏摩尔量是1mol B对整体热力学性质的贡献量, 而不应该理解为它在混合体系中所具有的量。
分类
气态混合物:空气 混合物液态混合物:甲醇 + 乙醇 固态混合物:Cu + Ni 气态溶液:萘溶解于高压CO 2中 非电解质溶液:糖水 − − − 本章 溶液液态溶液 电解质溶液:盐水 - - -电化学 固态溶液:单体溶解于聚合物中 − − − 又称固溶体
§4-2 化学势 化学势μ μB
• 4-2-1 化学势定义 • 4-2-2 平衡判据与平衡条件 • 4-2-3 理想气体的化学势表达式
4-2-1 化学势定义
混合物或溶液中,组分B的偏摩尔吉布斯函数 GB在化学热力学中有特殊的重要性,又把它叫 做化学势,用符号μB表示。
∂G µ B = GB = ∂nB T , p ,nc≠B
dX = ∑ X B dnB
B =1 k
( 2)
• 可得Gibbs-Duhem方程:
∑ n dX
B B=1
k
B
=0
∑ x dX
B B=1
k
B
=0
Gibbs-Duhem方程的意义: (1) 某一偏摩尔量的变化可从其它偏摩尔量的变 化中求得。 (2) 对一个含有K个组分的均相体系,K个偏摩 尔量Xi中,只有 K-1个是独立的。
如果在溶液中不按比例地添加各组分,则溶液浓 度会发生改变,这时各组分的物质的量和偏摩尔量均 会改变。 根据集合公式
4 多组分系统热力学

( p p* H 2 O ) 0.40 (105.4 7.33) 0.40kPa 39.23kPa
p N2 p p * H 2 O p H 2 (105.4 7.33 39.23) kPa 58.84kPa
M H 2 2.0158, x H2 pH2 k x,H2 M N 2 28.0134 mH2 / M H 2 m H 2O / M H 2O m H 2 / M H 2 m N 2 / M N 2 mH 2 / M H 2 m H 2O / M H 2O
* p甲苯 y苯
p p
* 苯
* 甲苯
y苯 p y苯
* 苯
38.7 0.3 0.142 ; x甲苯 1 x苯 0.858 100 38.7 0.3 100 0.3
4-6 在 18℃,气体的压力为 101.325kPa 下,1dm3 的水中能 溶解 O20.045g,能溶解 N20.02g。现 1dm3 将被 202.65kPa 空气饱 和了的水溶液加热沸腾,赶出所溶解 O2 的和 N2,并干燥之,求此 干燥气体在 101.325kPa、18℃下的体积及组成。设空气为理想 气体混合物,其组成(体积百分数)为: (O 解: M
x 2 d 2 RTdx2 x1 d 1 x 2 d 2
x 1 d 1 RTdx 2 RTd (1 x1 ) RTdx1
d1 RTdx1 / x1
1
1
d 1 RT d ln x1
x1 1
x1
1 1 RT ln x1 1 ( pg ) RT ln( p1* / p ) RT ln x1 1 1 ( pg ) RT ln( p1 / p )
4多组分体系热力学

多组分体系热力学1、不挥发的溶质溶于溶剂中形成溶液之后将会引起 蒸汽压降低 。
2、“在1θp 下,有0.002mol 的气体溶解在1000g 水中,当在相同温度下压力增大为2θp 时,就有0.004mol 该气体溶于1000g 水中”描述这一实验规律的定律是 亨利(Henry )定律 。
4、稀溶液的凝固点降低公式f m ⋅中,m 所代表的是稀溶液中f T K Δ= 溶质的质量摩尔浓度 。
6、25℃时,0.01m 糖水的渗透压为π1,0.01m 食盐水的渗透压为π2,则 π1<π2 。
7、若要使CO 2在水中的溶解度为最大,应选择的条件是 低温高压 。
8、理想溶液的通性是: 000V H S G Δ=Δ=Δ>Δ<混合混合混合混合0 。
9、在讨论稀溶液的蒸汽压降低规律时,溶质必须是 非挥发性物质 。
11、25℃时A 和B 两种气体在某一溶剂中溶解的亨利系数分别为k A 和k B ,且知k A >k B ,则当A 和B 压力相同时在该溶剂中所溶解的量是 A 的量<B 的量 。
10、对于A 和B 两种液体,在1θp 下,纯A 的沸点较纯的B 的沸点为高。
当A 和B 组成二元溶液时具有一恒沸混合物,则对于该恒沸混合物,其呈平衡的气相组成y 1与液相组成x 1之间 y 1=x 1 。
11、苯和甲苯能形成理想溶液,在20℃时,当1mol 苯和1mol 甲苯混合时,过程所对应的G Δ是 -3377J 。
23、在20℃时,将压力为θp 的1mol 气态NH 3溶解到大量组成为NH 3:H 2O=1:21的溶液中。
已知此溶液上NH 3的蒸气分压为27mmHg ,则该转移过程的为G Δ -8130J 。
26、0.005mol/kg 的硫酸钾水溶液其沸点较纯水的沸点升高了0.0073℃,已知水的质量摩尔凝固点降低常数K f 和沸点升高常数K b 分别为1.86及0.52,则该溶液的凝固点(以℃表示)为 0.00731.86C 0.52−×° 。
4-3多组分系统热力学-理想液态混合物与理想稀溶液
Physical Chemistry
物理化学(上册)
绪论 第一章 气体 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分系统热力学 第五章 化学平衡 第六章 相平衡
第四章 多组分系统热力学
§4-!本章基本要求 §4-1多组分系统热力学概念 §4-2拉乌尔定律与亨利定律 §4-3偏摩尔量 §4-4化学势 §4-5理想液态混合物 §4-6理想稀溶液 §4-7活度活度系数 §4-8化学势小节 §4-$小结与学习指导
d* S*dT V *dp
B
B
B
mixG p
T
B
nBVB
B
nBVB* mixV
2. mixV 0 或 V mix m 0
mix p
G
T
(RT
nB ln xB )
B
p
T
0
§4-5理想液态混合物
四、理想液态混合物混合性质
dG B S B dT VB dp
dG * S * dT V *dp
B
B
6.
mixU mix H P mixV 0
mixU 0 或 mixU m 0
§4-5理想液态混合物
四、理想液态混合物混合性质
小结: 1. mixV=0 , mixU=0 , mixH=0 2. Q=0, W=0 3. mixS=-RnBlnB>0 (绝热 S>0)
mixA=RTnBlnB<0 (恒温恒容W =0 A<0) mixG=RTnBlnB<0 (恒温恒压W =0 G<0)
§4-6理想稀溶液
一、理想稀溶液定义 无限稀溶液,溶质的浓度趋于零的溶液。 对溶剂(A表示)用符合拉乌尔定律
物理化学第四版 第四章 多组分系统热力学2014.2
)
p,n
(
B
)
,V
(
G P
)T
,n(
B
)
k
dG SdT VdP BdnB
证毕
B 1
14
又 dA d(G PV ) dG pdV Vdp
将上式dG 代入,整理得:
k
dA sdT PdV BdnB ……..(3) B 1
同理可得出另二个热力学基本方程。
因 A=A(T,V,n1,n2…….nk)
B
B
B
........
n B
相平衡条件
有N 个组分,就有N 个这样的式子
19
例:在、 两相中均含有A和B两种物质,达到相平衡时,下列
各式正确的是(
)。
A、
A
B
B、
B
B
C、
A
B
D、
B
A
例:组分B从相扩散入相中,则以下说法正确的有( A、总是从浓度低的相扩散入浓度高的相 B、平衡时两相浓度相等 C、总是从化学势高的相移向低化学势低的相
dA
(
A T
)V
,n
(
B
)
dT
( A V
)T ,n(B)
dV
k B 1
(
A n(B)
)T
,V
,n
(
c,c
B)
dnB
将式(4)和式(3)比较
B
A ( nB
)T ,V ,n(c,cB)
同样可得出
B
U ( nB
)S ,V ,n(c,cB)
H ( nB
)S ,P.n(c,cB)
…..(4)
15
例 2: 下列偏导数中那些是偏摩尔量?那些是化学势?
大学物理化学经典课件4-3-多组分体系热力学
本课程旨在帮助学生掌握多组分体系热力学的基本概念、原理和 方法,培养学生运用热力学原理分析复杂体系的能力,为后续的 科研和工程实践打下基础。
多组分体系热力学概述
定义与特点
多组分体系是指由两种或两种以上不同物质组成的体系。多 组分体系热力学主要研究这类体系的热力学性质及其变化规 律,包括相平衡、化学平衡、能量转换等内容。
溶液的理论来处理真实溶液的问题。
活度系数
活度系数是描述真实溶液与理想溶液差异程度的物理量,它与溶液中的离子强度、溶剂 化作用等因素有关。活度系数的引入使得我们可以更准确地描述真实溶液的性质和行为。
03
多组分体系的相平衡
相律与相图
相律
描述多组分体系相平衡的基本规律, 即体系自由度、组分数和相数之间的 关系。
理论联系实际
将所学理论知识与实际问题相结合,通过分析和 解决具体问题来加深对理论知识的理解。
多做习题
通过大量的习题练习,可以巩固所学知识,提高 分析问题和解决问题的能力。
领域前沿与展望
新理论和新方法
随着科学研究的不断深入,多组分体系热力学领域不断涌现出新的理论和方法 ,如非平衡态热力学、微观热力学等,为相关领域的发展提供了新的思路。
电镀
利用电解原理在某些金属表面镀 上一薄层其他金属或合金的过程, 多组分体系热力学对于控制镀层 质量和厚度具有重要意义。
电解
通过电流作用使物质发生化学变 化的过程,多组分体系热力学研 究有助于降低能耗和提高产率。
高分子溶液中的应用
高分子合成
通过控制反应条件,合成具有特定结构和性能的高分子化合物,多 组分体系热力学研究有助于优化合成路线和提高产率。
相图
用图形表示多组分体系在不同条件下 的相平衡关系,包括温度、压力、组 成等。
物理化学课件及考试习题 试卷 答案第4章 多组分系统热力学习题及答案
第三章多组分系统热力学一、填空题1、只有系统的____性质才具有偏摩尔量。
而偏摩尔量自身是系统的____性质。
偏摩尔量的值与系统中各组分的浓度____。
混合适物系统中各组分的同一偏摩尔量间具有两个重要的性质,分别是____与____。
2、如同温度是热传导的推动力一样,化学势是____传递的推动力。
在恒温恒压下多相平衡的条件是________________。
以焓表示的组分i的化学势可写成µi=____。
3、混合理想气体中任一组分B的化学势________;理想溶液中任一组分B的化学势________;稀溶液中溶剂A的化学势________。
4、由纯组分在恒温恒压下组成理想混合物时,△mix S=__0;△mix G__0;△mix H__0;△ix V__0。
5、理想溶液混合时,∆mix V ,∆mix S ,∆mix G ,∆mix H 。
6、比较水的化学势的大小(此处p=101.325kPa):(填>、< 或=)①μ(l,100℃,p)____μ(g,100℃,p)②μ(l,100℃,p)____μ(l,100℃,2p)③μ(g,100℃,p)____μ(g,100℃,2p)④μ(l,100℃,2p)____μ(g,100℃,2p)⑤μ(l,101℃,p)____μ(g,101℃,p)7、非理想溶液溶质的化学势表示式____,其标准态为____。
8、在一定的温度及压力下,某物质液汽两相达平衡,则两相的化学势μB(l)与μB(g)_____若维持压力不变,升高温度,则μB(l)和μB(g)都______;但μB(l)比μB(g)______。
9、理想溶液中任意组分B的化学势:μB=_______________。
10、298K、101.325kPa,有两瓶萘的苯溶液,第一瓶为2升,溶有0.5mol萘,第二瓶为1升,溶有0.25mol 萘,若以μ1和μ2表示两瓶中萘的化学势,则它们的关系为__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Tf K f bB
2014-7-21
2.7 纯物质两相平衡方程(P55)
Clapeyron方程: 两相平衡时温度和压力间的关系
2014-7-21
得:
移项: 整理得:
代入得:
2014-7-21
纯物质液-气、固-气平衡:
Vm Vm g Vm l Vm g Vm Vm g Vm s Vm g dp vap H m vap H m p dT TVm g Tp Vm g
组分浓度关系
* A
p p p p xB
* B * A
2014-7-21
x A 1 xB
——理想溶液蒸汽压与浓度xB的关系
图形表示
p
p p A pB
* p p p A A
0 xB 1
* pB pB p
p A p* A xA
* pB pB xB
2014-7-21
第五章 多组分系统热力学
5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10
2014-7-21
引言 偏摩尔性质 化学势μ B 稀溶液的气液平衡 理想稀溶液 稀溶液的依数性 理想溶液 活度 活度和活度系数的测定 超额函数与规则溶液 溶液中的化学平衡
(2) 开始沸腾时第一个气泡的组成,即上述溶液的平衡气 相组成,设为yB, 则 yB P PB PB xB
PB xB 0.726 0.666105 Pa yB 0.477 5 P 1.01310 Pa y A 1 yB 1 0.477 0.523
2014-7-21
5.6.2 理想溶液中组分的化学势
(理想液态混合物中任意组分的化学势)
5.6.3 理想溶液的混合性质
(理想液态混合物的混合性质)
2014-7-21
5.6.1 理想溶液的蒸汽压
1、宏观模型
设A+B→理想溶液,气液平衡时
(理想溶液模型)
p A p* A xA ;
* pB pB xB
* p p A pB p *来自x p A A B xB稀溶液
两个模型
稀溶液 理想溶液
上次课内容
稀的量化: 蒸汽压浓度 Raoult’s Law Henry’s Law
pA p x
* A A
溶剂 溶质
p B k x xB
A
B ,b
理想稀溶液:溶剂
A (T ) RT ln xA
溶质 B ,b
c B,%B B ,%B (T ) RT ln%B
vap H m 1 1 p2 定积分 ln p1 R T2 T1
液体或固体的饱和蒸汽压
pVm g RT
d ln p vap H m dT RT 2
sub H m p2 ln p1 R
1 1 T T 1 2
标准态的化学势是温度T,压力为p下液体纯物质B 的化学势,用 B (l , T ) 表示。 p与p的差别引起的 得到:
* B p
* B (l , T )与 B (l , T , p)的差别可由下式
* V B ,m T
dG SdT VdP Gi dni
例100℃时,纯CCl4及纯SnCl4的蒸气压分别为
2014-7-21
二组分液态完全互溶系统的沸点-组成图
2014-7-21
解: 分别以A和B代表CCl4和SnCl4,则
PA 1.933105 Pa PB 0.666105 Pa (1) P PA ( PB PA ) xB 5 5 P PA 1.01310 Pa 1.93310 Pa xB 0.726 5 5 PB PA 0.66610 Pa 1.93310 Pa
(1)偏差系数,又叫活度系数。 (2)渗透因子:描述真实溶液的溶剂对理想稀溶液的 偏差。 (3)超额函数:衡量整个溶液的不理想程度。
3、产生偏差的原因
(1)物理作用 不易挥发 形成溶液后分子间作用力发生变化
fA-B >fA-A>fB-B fA-B <fA-A<fB-B
V 0 引起负偏差 V 0 引起正偏差
T
R ln xB
H m ,B HB 2 2 T T
*
即 HB H
* B,m
* mix H H混合后 H混合前 nB ( H B H B ,m ) 0 B
2014-7-21
3.ΔmixG与ΔmixS
mix G G混合后 G混合前
B B B
* * nB B nB B B B nB
糖水溶液
μA(l, xA)+dμA(l, xA)=G*m,A(s)+dG*m,A(s) dμA(l, xA)=dG*m,A(s)
2014-7-21
μA(l,xA)=f (T,p,xA)
G *m,A(s)=f (T,p)
则P不变,T及xA变化时,以上函数的全微分为
所以:
SA
2014-7-21
dG SdT VdP Gi dni
mixV V混合后 V混合前
* nBVB nBVB ,m 0 B B
2014-7-21
2. mixH =0 由
* B (T , p) B (T , p) RT ln xB
B (T , p)
T
* B (T , p)
* * ( T ) ( B B B) 0 T p ,nB T p , nB
S
CaS
P131例5-3:利用凝固点下降常数求尿素的摩尔质量
2014-7-21
凝固点降低推导
设有一稀溶液,溶剂摩尔分数为xA,该溶液在压力P时, 凝固点为T。在T, P下建立凝固平衡时,表示如下:
冰
μA(l,xA)=G *m,A(s)
在P一定时,若xA→xA+dxA,而相应的 凝固点由T→T+dT,在此条件下再建立 新的凝固平衡。这时由平衡条件,应有:
2014-7-21
3、产生偏差的原因
(2)化学作用
形成溶液时产生分解、缔合或形成化合物 分解: 大分子→小分子 缔合: 小分子→大分子 引起正偏差 引起负偏差
2014-7-21
5.5.2 理想溶液中组分的化学势
气液平衡时 μB(l)=μB(g) 理想气体
Raoult’s定律
——纯液体B的标准化学势
B (T , p) RT ln xB
* B
2014-7-21
——理想溶液中组分B的化学势
注意:
的化学势。
* B (l , T , p) 不是标准态
2 B 3 B
2014-7-21
xB M AbB
令:K RT f
则: T f
* 2 f
RT
M
* 2 f
A
M
fus H
* m, A
bB
A
* fus H m ,A
凝固点降低常数
K mol1 kg 。
常用溶剂的 kf 值有表可查。用实验测定 Tf 值,查出 kf ,就可计算溶质的摩尔质量。 则:
x A 1 xB 0
2014-7-21
A
xB
B
xB 1 x A 0
2、微观模型 (1)fAA=fBB=fAB
(2)V(A分子)=V(B分子) 根本原因就是它们的化学性质及分子内部结构非 常相似。 例:同位素混合物(H2O+D2O) 同分异构体(对、邻或间二甲苯) 同系物(苯+甲苯;正己烷+正庚烷) 冶金上的炉渣
2014-7-21
B ,c (T ) RT ln
B ,c
bB (T ) RT ln b cB
上次课内容
分配定律应用:
i (缔合)
cB 在定温、定压下,互不相溶两稀溶液 K cB
i (分解)
炼钢脱硫(S萃取):
渣+ CaO
钢
依数性应用:
计算溶液的分子量
设ΔTf=T f-Tf,则
*
T f
RT T H
* f f * fus m , A
ln x A
适用于理想溶液和稀溶液,精确求Tf
2014-7-21
再加两个近似条件: (i) 对稀溶液TfT *f=(T *f)2 (ii)因为xB<<1,
x x ln x A ln1 xB xB xB 2 3 * 2 RT f 则: T f xB * fus H m, A
解: 符合H定律条件 PB kbbB
T1 273K : P 1 kb1 b 1 T2 303K : P2 kb2 b2
p2 P2m2 b2 pk km , b1 kb2p 1 P 1m1 b1 p2 H 1 1 13020 30 ln 0.568 p1 R T1 T2 8.314 273 303 2014-7-21 p2 1.76 p1 0.37 p
vap H m p 不定积分 ln B Pa R
液-气两相平衡,液体饱和蒸汽压 2014-7-21
sub H m p ln B Pa R
固-气两相平衡,固体饱和蒸汽压
例:一个海洋生物学家饲养某种习惯于在 0 ℃左右水中 生活的鱼类,他希望这种鱼能在30℃的水中生活。他想 把 30℃水中溶解氧的浓度保持在 0℃水中的浓度。为了 达到这一目的,计算鱼缸上方应保持氧的压力是多少? 溶解氧对水中氧溶解度的影响可以略去不计。
