FR共轭梯度法
fr共轭梯度法matlab程序

fr共轭梯度法matlab程序简介在优化问题中,求解大型的线性方程组是一项基本的任务。
共轭梯度法(Conjugate Gradient Method)是一种迭代法,用于求解形如Ax=b的线性方程组,其中A是一个对称正定矩阵,b是一个向量。
fr共轭梯度法是共轭梯度法的一种变形,它引入了Fletcher-Reeves公式,可以更快地收敛到解。
本文将详细介绍fr共轭梯度法的原理,并给出基于Matlab的实现示例,帮助读者更好地理解和应用该算法。
fr共轭梯度法原理共轭梯度法回顾在介绍fr共轭梯度法之前,我们先回顾一下共轭梯度法的原理。
共轭梯度法是一种迭代法,用于求解形如Ax=b的线性方程组。
它的基本思想是通过不断迭代的方式逼近线性方程组的解。
具体步骤如下:1.初始化:令x0为一个初始向量,r0=b-Ax0为初始残差,p0=r0为初始搜索方向。
2.迭代更新:根据一定的更新规则,计算新的搜索方向pk和步长αk,用于更新解向量xk+1。
3.残差更新:计算新的残差rk+1=b-Axk+1。
4.判断终止条件:如果满足终止条件,算法停止;否则返回步骤2。
共轭梯度法的关键在于如何选择搜索方向和步长。
在每次更新解向量时,搜索方向选择为残差的线性组合,即pk=rk+βkpk-1,其中βk由Fletcher-Reeves公式确定。
步长选择为使目标函数在搜索方向上取得最小值的约化步长。
fr共轭梯度法改进fr共轭梯度法是对共轭梯度法的一种改进,它引入了Fletcher-Reeves公式。
Fletcher-Reeves公式是通过计算两次迭代时的梯度向量的内积得到的。
具体表达式如下:βk = (rk+1’ * rk+1) / (rk’ * rk)其中rk为残差向量。
通过引入Fletcher-Reeves公式,fr共轭梯度法在选择搜索方向时更加准确,可以更快地收敛到解。
fr共轭梯度法的Matlab实现在Matlab中,我们可以通过编写相应的程序来实现fr共轭梯度法。
运筹学实验共轭梯度法
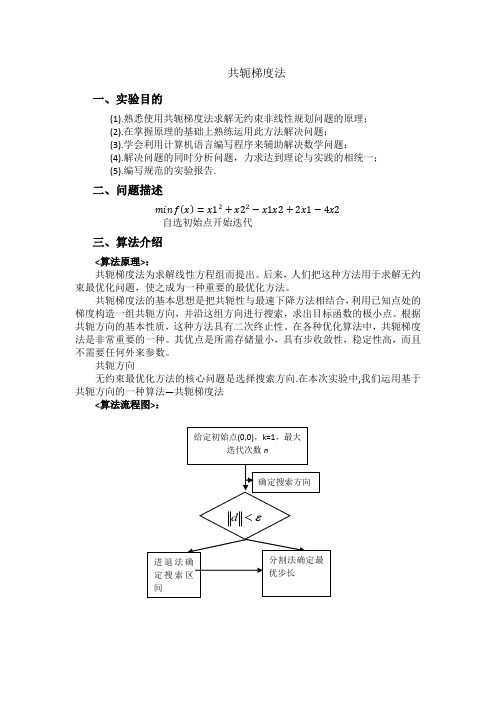
共轭梯度法一、实验目的(1).熟悉使用共轭梯度法求解无约束非线性规划问题的原理;(2).在掌握原理的基础上熟练运用此方法解决问题;(3).学会利用计算机语言编写程序来辅助解决数学问题;(4).解决问题的同时分析问题,力求达到理论与实践的相统一;(5).编写规范的实验报告.二、问题描述自选初始点开始迭代三、算法介绍<算法原理>:共轭梯度法为求解线性方程组而提出。
后来,人们把这种方法用于求解无约束最优化问题,使之成为一种重要的最优化方法。
共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点。
根据共轭方向的基本性质,这种方法具有二次终止性。
在各种优化算法中,共轭梯度法是非常重要的一种。
其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
共轭方向无约束最优化方法的核心问题是选择搜索方向.在本次实验中,我们运用基于共轭方向的一种算法—共轭梯度法<算法流程图>:四、程序%¾«È·ÏßËÑË÷,ÌݶÈÖÕÖ¹×¼Ôòfunction [ m,k,d,a,X,g1,fv] = GETD( G,b,c,X,e,method)if nargin<6error('ÊäÈë²ÎÊý±ØÐëΪ6');endn=length(G);if n==2format long e%ratsyms x1x2f=1/2*[x1,x2]*G*[x1;x2]+b'*[x1;x2]+c;g=[diff(f,x1);diff(f,x2)];g1=subs(subs(g,x1,X(1,1)),x2,X(2,1));d=-g1;a=-(d'*g1)/(d'*G*d);% a=-((X(:,1)'*G*d+b'*d)/(d'*G*d)); a=g1(:,1)'*g1(:,1)/(d(:,1)'*G*d(:,1));X(:,2)=X(:,1)+a*d;g1=[g1 subs(subs(g,x1,X(1,2)),x2,X(2,2))];m1=norm(g1(:,1));m=norm(g1(:,2));i=2;k=zeros(1);switch methodcase'FR'while m>=ek(i-1)=(m/m1)^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));%a1(i)=-((X(:,i)'*G*d(:,i)+b'*d(:,i))/(d(:,i)'*G*d(:,i)));a (i)=g1(:,i)'*g1(:,i)/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endcase'PRP'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(norm(g1(:,i-1)))^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'HS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(g1(:,i)-g1(:,i-1))); d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'DY'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(g1(:,i)-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'LS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'CD'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'WYL'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-(m/m1)*g1(:,i-1))/(m1^2);d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endendfv=subs(subs(f,x1,X(1,i)),x2,X(2,i));endl1=X(1,i);l2=X(2,i);w1=X(1,1);w2=X(2,1);v1=min(l1,w1)-abs(l1-w1)/10:abs(l1-w1)/10:max(l1,w1)+abs(l1-w1)/10;v2=min(l2,w2)-abs(l2-w2)/10:abs(l2-w2)/10:max(l2,w2)+abs(l2-w2)/10; [x,y]=meshgrid(v1,v2);s=size(x);z=zeros(size(x));for i=1:s(1)for j=1:s(2)z(i,j)=1/2*[x(i,j),y(i,j)]*G*[x(i,j);y(i,j)]+b'*[x(i,j);y(i,j)]+c;endend[px,py] = gradient(z,.2,.2);contour(v1,v2,z), hold on, quiver(v1,v2,px,py)[C,h] = contour(x,y,z);set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)x1=X(1,:);y1=X(2,:);plot(x1,y1,'r*:');五、计算结果如图所示,输入>> G=[2,-1;-1,2];>> b=[2;-4];>> c=0;X=[1;1];e=1e-3;method='FR';表示正定矩阵为G,b为一次元系数矩阵,c为常数0,X是初始迭代点,e 为精度,method为共轭梯度的公式方法。
共轭梯度法

•基本思想:把共轭性与最速下降法相结合,利用已 知点处的梯度构造一组共轭方向,并沿着这组方 向进行搜索,求出目标函数的极小点
4.4共轭梯度法
先讨论对于二次凸函数的共轭梯度法,考虑问题
min f (x) 1 xT Ax bT x c
3, giT d (i) giT gi (蕴涵d (i) 0)
证明: 显然m1,下用归纳法(对i)证之.
当i 1时,由于d (1) g1,从而3)成立,对i 2时, 关系1)和2)成立,从而3)也成立.
4.4共轭梯度法
设对某个i<m,这些关系均成立,我们证明对于i+1
也成立.先证2),
因此
2 / 3 1 5/ 9
d (2)
1/ 1
3
1 9
2 0
5/9 1
从x(2)出发,沿方向d (2)进行搜索,求步长2,使满足 :
f
( x (1)
2d (1) )
min
0
f
(x(2)
d (2))
2 0
4.4共轭梯度法
显然, d (1)不是目标函数在x(1)处的最速下降方向.
下面,我们用FR法构造两个搜索方向.
从x(1)出发,沿方向d (1)进行搜索,求步长1,使满足 :
f
( x (1)
1d (1) )
min
0
f
( x (1)
d (1) )
得1 2 3
A正定,故x是f(x)的极小值点.
共轭梯度法

必有
p
T j
∇f
(X
n
)
=0(源自j=0,1,L,
n
− 1)
因为A正定,所以f (X ) 是凸函数,故 X n 是惟一的全局 极小点。
从而
∇f (Xk ) = AXk + b
=
AX
j+1
+
λ* j+1
Apj+1
+L+
λ* k −2
Apk−2
+
λ* k −1
Apk
−1
+
b
=
∇f
(X
⎡6 ⎢⎣17
12⎤ 17⎥⎦
⎢⎣⎡−
90 289
−
210⎤ 289⎥⎦
T
−
210⎤⎡ 3 289⎥⎦⎢⎣−1
−11⎥⎦⎤⎢⎣⎡−
90 289
−
210⎤T 289⎥⎦
= 17 10
X2
=
X1
+
λ1 p1
=
⎡ 26 ⎢⎣17
38 ⎤ T 17 ⎥⎦
+ 17 10
⎢⎣⎡−
90 289
−
210 ⎤ T 289 ⎥⎦
= [1
1]T
∇f ( X 2 ) = [0 0]T
练习: 试用共轭梯度法二次函数
min
f
(x)
=
x12
+
1 2
x22
+
1 2
x32
的极小点。取初始点为x( 0 ) = (1,1,1)T
3 、非二次函数的共轭梯度法
一般地,我们有:
⎧ X k+1 = X k + λk pk
共轭梯度法

2 2 min f ( x ) = x1 + 2x2 x
⎛1⎞ 给定初始点 x (0) = ⎜ ⎜1⎟ ⎟。 ⎝ ⎠
13
⎛ 2 x1 ⎞ ⎛ 2 0⎞ 2 首先, ∇f ( x ) = ⎜ ⎜ 0 4⎟ ⎟ ,以下利用(4.14)确定 β k 。 ⎜ 4x ⎟ ⎟ ,H= ∇ f ( x ) = ⎜ ⎝ ⎠ ⎝ 2⎠ k=0:
0
k +1
) 与搜索方向 s 0 ," , s k 均正交。同时,利用引理 4.1 马上
设 H ∈ R n×n 是对称正定阵,s ," , s
0
n −1
0
n −1
是非零 G—共轭方向组,x ∈ R 。 若对问题(UQP),
0
n
从 x 出发,依次沿 s ," , s
0
进行最优一维搜索,最终得到 x ,则 x 是(UQP)的最优解。
为保证 H-共轭性,在 x 处必须取 s 为搜索方向,而不能取 α s (α > 0) 为搜索方向。
k k
k
利用定理 4.3,马上得到上述算法的有限终止性。 定理 4.4 设 H ∈ R n×n 是对称正定阵。若用凸二次规划的共轭梯度法求解 (UQP) 时产生迭代点
x1 ," , x K ,则 x K 是(UQP)的最优解,并且 K ≤ n 。
首先由(4.7)知, g = ∇f ( x ) ( j = 0, " , k -1)是 s ," , s 的线性组合,因此根据定理 4.2,
j j 0 j
( g k )T g j =0, j = 0, " , k -1
由于
(整理)16梯度法和共轭梯度法基本原理和特点.

16梯度法和共轭梯度法基本原理和特点?梯度法又称最速下降法,基本原理是在迭代点附近采用使目标函数值下降最快的负梯度方向作为搜索方向,求目标函数的极小值,特点;迭代计算简单,只需求一阶偏导数,所占的存储单元少,对初始点的要求不高,在接近极小点位置时收敛速度很慢,共轭的特点为在梯度法靠近极值点收敛速度放慢时,它可以构造共轭方向使其收敛速度加快,迭代计算比较简单,效果好,在每一步迭代过程中都要构造共轭的、方向,比较繁琐。
17迭代终止准则有哪三种?1)当设计变量在相邻两点之间的移动距离充分小时,可用相邻两点的矢量差的模作为终止的判据,2)当相邻两点目标函数值之差达到充分小时,可用两次迭代的目标函数之差作为终止判据。
3)当迭代点逼近极值点时,目标函数在该点的梯度已达到充分小时,可用梯度的模作为终止判据。
18.无约束设计法,1)powell法,它是在下降迭代过运算中只需计算和比较目标函数值的大小,不需计算偏导数的方法,是较好的一种直接搜索算法。
2)梯度法,又称最速下降法,它是采用使目标函数值下降最快的负梯度方向作为搜索方向来求目标函数的极小值。
3)共轭梯度法,又称FR法,是利用目标函数的梯度确定共轭方向,使得计算简便而效果好,只需利用相邻两点的梯度就可以构造一个共轭方向,这种方式产生共轭方向并进行迭代的算法称为共轭梯度法。
4)变尺度法,又称DFP法,为了得到既有快速收敛的性质,又能避免计算二阶导数矩阵及逆矩阵,减少计算工作量。
迭代公式X=X+aS,19有约束设计法?1)复合形法,在可行域中选取k个设计点作为初始复合形的顶点,然后比较复合形个各项目标函数值的大小,其中目标函数值最大的点为坏点,以坏点之外其余各点的中心为映射中心,寻坏点的映射点,以映射点替换坏点,并与原复合型除坏点之外其余各点构成就k 顶点的新的复合型,这样反复迭代直到达到精度找到最优点,2)简约梯度法,用来解决线性约束非线性规划问题。
3)罚函数法,是把一个有约束的问题转化为一系列无约束的问题求解,逐渐逼近最优值。
FR共轭梯度法的理论推导

∴ pm +1与p0, pm-1 , A共轭 ...,
k = 0,1, 2,...., n − 1 ∇f ( X ( k +1) )T pk = 0,
∴[∇f ( X ( k ) ) + λk Apk ]T pk = 0, [∇f ( X ( k ) )]T pk [ pk ]T ∇f ( X ( k ) ) λk = − =− T pk Apk pk T Apk
但还需证明pm +1与p0, pm-1 , A共轭 ...,
0 ≤ j ≤ m −1 Q pm +1T Ap j = [−∇f ( X ( m +1) ) + α m pm ] Ap j = −∇f ( X ( m +1) )T Ap j Q λ j pm +1T Ap j = λ j [−∇f ( X ( m +1) )T Ap j ] = −∇f ( X ( m +1) )T λ j Ap j = −∇f ( X ( m +1) )T [∇f ( X ( j +1) ) − ∇f ( X ( j ) )] =0
∴∇f ( X ( n ) ) = 0 ∴ X ( n )为f ( X )的极小点X *
2 FR公式推导
X ( k +1) = X ( k ) + λ k p k , 其 中 : λk = − pT ∇f ( X (k ) ) k p k Ap k
( k +1)
T
, (λk =
∇f ( X (k ) ) p Ap k
T k
2
)
(1)
k = 0,1, ..., n − 1
p
k +1
= −∇ f (X
共轭梯度法

, k 1 )
(1)
同样由前一节共轭方向的基本定理有:
T gk di 0
( i 0,
, k 1 ),(2)
T 再由 g i 与 d i 的关系得: gk gi 0 ( i
0,
i 0,
, k 1 )
(3)
将(2)与(3)代入(1)得:当 而
i 0 , k 2 时,
第 2次迭代:
5 2 8 T ( 8 , 4 )T ( , ) 18 9 9
g1 (
8 2 16 2 ) ( ) || g1 || 9 9 4 . 0 || g 0 ||2 82 4 2 81
2
8 16 T , ) . ||g1 || 9 9
解:
4 1 f ( x) ( x1 , x2 ) 2 0
0 x1 , 2 x2
4 0 G . 0 2
f ( x) ( 4 x1 , 2 x2 )T .
第1 次迭代:
令
而
d (0) g0 f ( x(0) ) ( 8 , 4 )T ,
一、共轭梯度的构造 (算法设计针对凸二次函数) 设
f ( x)
1 T x Gx bT x c 2
其中 G 为 n n 正定矩阵,则
g ( x) Gx b
对二次函数总有 1)设
gk 1 gk G xk 1 xk k Gdk
,令 x1 x0 0 d0 ( 0 为精确步长因子)
dk 1 f ( xk 1 ) dk
|| f ( xk 1 ) ||2 || f ( xk ) ||2
令k=k+1;返回4.
