卷积积分
合集下载
卷积积分及零状态响应的卷积计算法.
t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积,实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义,函数在0到t区间内的定积分值,决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
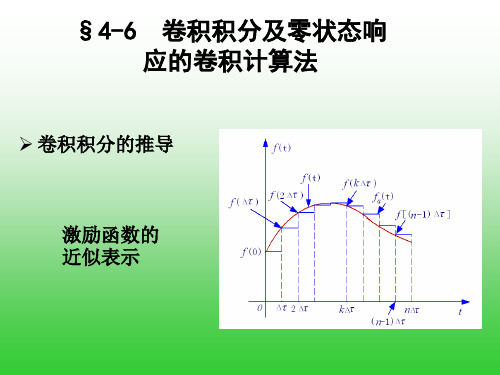
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解: [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解: 用卷积积分公式求uC(t),应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限
卷积分

-T0
T0 h(-T0/2- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
(7) t= -T0时,y( -T0)=A T0
2
x(t)
y(t) 2A2T0
-T0
T0 h(-T0- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
x(t)
(8) t= -3T0/2时,y( -3T0/2)=3A2T0/2
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
x(t)
(5) t= 2T0时,y(2T0)=0
y(t) 2A2T0
-T0
T0 h(T0/2- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
(6) t= -T0/2时,y( -T0/2)=3A T0/2
2
x(t)
y(t) 2A2T0
x(t)
(1)反折; 反折; 反折 (2)平移; 平移; 平移
0 t (4)积分
h(t)
(3)相乘; 相乘; 相乘 (4)积分。 积分。 积分
t
0
t (1) (1)反折
x(t)
h(-τ)
0 x(t) h(t1 -τ)
0
τ
(2)平移
(3)相乘
h(t1 -τ)
tτ
00
0
τ
卷积与相关
4 含有脉冲函数的卷积 • 设 h(t)=[δ(t-T)+ δ(t+T)] • 卷积为
卷积与相关
• 例 三角脉冲频谱计算
x(t) h(0-τ)
第二章 (4)卷积积分的性质

f 1 (t )
f 2 (t )
2
1
0
2
0 1
1
2 3
t
1
3
t
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
f (t ) = 0
2
0
1
2 3
τ
f 2 (t τ
t2
)
1
t 0
1
τ
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
t
f (t ) = 0
1< t < 2 ,
f (t ) = ∫ 2dτ = 2(t 1)
(2) e ε(t + 3) ε(t 5) 2t e ε (t + 3) ε (t 5) ∞ 2τ = ∫ e ε (τ + 3) ε (t τ 5)dτ ∞
2t
=∫t 53e2τ1 2(t 5) 6 e = e 2 6 1 2( t 2) = e 1 e 2
[
1 2τ dτ = e 2
' ∞ ∞
上式称为杜阿密尔积分. 上式称为杜阿密尔积分. 杜阿密尔积分 其物理含义为: 其物理含义为:LTI系统的零状态响应等于激励的 系统的零状态响应等于激励的
f ' (t )与系统的阶跃响应 g(t )的卷积积分. 的卷积积分. 导数
例2.4-4 求图示函数 f1(t ) 与 f2 (t ) 的卷积 f (t ) .
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2 )
推广4 推广
Z2.14 卷积积分的图解法

2
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
第二章 连续系统的时域分析
例1 f (t), h(t) 如图,求yzs(t)= h(t) * f (t) 。 f (-τ ) f ( τt )
解:
h(t)函数形式复杂, 换元为h(τ); f (t)换元为 f (τ)
2
② 0≤t ≤1时 ③ 1≤t ≤2 时
yzs (t)
t 1 d 1 t2
02
4
yzs (t)
t 1 d 1 t 1
t1 2
24
0 t t-11 tt-1 2 3 t yf (t )
④ 2≤t ≤3时
yzs (t)
2 1 d 1 t2 1 t 3
t1 2
4 24
f (τ)反折→ f (-τ)平移t f(t -τ) ① t < 0时 , f (t -τ→)向左移
f ( t -τ) h(τ) = 0,故 yzs(t) = 0 t>0 时, f (t -τ)向右移
f (t -τ ) t-1 t
01
τt
1 h ( tτ ) 2
பைடு நூலகம்
0
2
t-1 t t-1 t 2
τt
h(τ )f (t -τ ) 1
例2 f1(t), f2(t)如图,已知 y(t) = f1(t)* f2(t),求y(6) =?
解:
y(6)
f1( )
f2 (6
) d
4
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
y(6)
通信技术概论3.4卷积积分的物理解释和性质2012

f (t ) * (t t 0 ) (t t 0 ) * f (t ) f (t t0 )
三、卷积积分的应用
(t )
e(t) r(t) r ( t ) e ( t ) * h( t )
即
线性网络 零状态
t
h(t)
r (t ) e( )h(t )d
卷积积分
一、卷积积分(Convolution)的定义 定义:设 f1(t), f2(t) t < 0 均为零
f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d
t 0
二、卷积积分的性质 性质1
f1 ( t ) * f 2 ( t ) f 2 ( t ) * f 1 ( t )
0
物理解释: 将激励 e(t)看成一系列宽度为 ,高度为 e(k )矩形脉冲叠加的。
e(t )
e(0)
o
2
k (k+1)
t
e(t ) e(0)[ (t ) (t Δ )] e(Δ )[ (t Δ ) (t 2Δ )]
e(kΔ ) p(t kΔ ) Δ
k 0
k 0
响应 r (t ) e(k ) hp (t k )
当e(t )分割得足够细 即N ,
激励 e( t ) lim
N
e(kΔ ) p(t kΔ ) Δ
k 0
N
(t )
冲激
脉冲
响应 r ( t ) lim e( kΔ )hp ( t kΔ )Δ
积分
N k 0
N
脉冲响应
h(t )
冲激响应
卷积积分公式

卷积积分公式
卷积积分公式是一种数学运算,用于计算两个函数的卷积。
卷积是一种线性运算,用于描述两个函数之间的关系。
设有两个函数f(x)和g(x),其卷积定义为:
(f * g)(x) = ∫f(t)g(x-t)dt
其中*表示卷积运算符,∫表示积分运算。
这个公式可以理解为,在函数g(x)上取一个滑动窗口,窗口的大小为函数f(x)的长度,然后计算窗口内两个函数的点积,并将结果在x上求和作为卷积结果。
卷积积分公式可以应用于信号处理、图像处理、物理学等领域,用于分析信号的频率特性、图像的模糊效果等。
卷积积分及其性质 ppt课件

d dx
(t)是奇函数 [ (x t)] f (x) d x [ f (t)] f (t)
第2-15页
PPT课件
15
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2.4 卷积积分的性质
3. f(t)*ε(t)
t
f ( ) (t ) d f ( ) d
¥
ò yzs (t) =f (t) * h(t) =
et [6 e- 2(t- t )- 1]e(t - t ) d t
-?
当t <τ,即τ> t时,ε(t -τ) = 0
蝌t
yzs (t) =
et [6 e- 2(t- t )- 1]d t =
-?
t
(6 e- e2t 3t - et ) d t
?
(t)
t0
)
f
(
t
)
d
t
f (t0)
'(t) f (t) d t f '(0)
PPT课件
(t
t0 )
f
(t) d t
f
(t0 )
16
第2-16页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2.4 卷积积分的性质
三、卷积的微积分性质
1.
dn dtn
第2-11页
PPT课件
11
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2.4 卷积积分的性质
下面讨论均设卷积积分是收敛的(或存在的)。
卷积积分的运算

§2.5 卷积积分的运算和图解
y(t) x(t) h(t) x( )h(t )d
1)将x(t)和h(t)中的自变量由t改为,成为函数的自 变量; 2)把其中一个信号翻转、平移;
h( ) 翻转h( ) 平移th(( t)) h(t )
3)将x() 与h(t )相乘;对乘积后的图形积分。
例11:画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例:引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12:根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10:试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式,可直接画出系统模拟图
y(t)
y(t) x(t) h(t) x( )h(t )d
1)将x(t)和h(t)中的自变量由t改为,成为函数的自 变量; 2)把其中一个信号翻转、平移;
h( ) 翻转h( ) 平移th(( t)) h(t )
3)将x() 与h(t )相乘;对乘积后的图形积分。
例11:画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例:引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12:根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10:试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式,可直接画出系统模拟图
y(t)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
τ
∴yzs (t) = ∫ f (τ)h(t τ)d τ
t0
t
2.物理意义: 2.物理意义: 物理意义 LTIS在任意时刻 LTIS在任意时刻t对任意激励的零状态响应等于从激励函 在任意时刻t 数开始作用的时刻( 数开始作用的时刻( = t0 到指定时刻(τ = t 区间内,无 )区间内, τ )到指定时刻( 穷多个幅度不同,连续出现的冲击响应的总和. 穷多个幅度不同,连续出现的冲击响应的总和. 这就是说,输入f 这段时间内电路的连续作用, 这就是说,输入f(t)从t=t0到t 这段时间内电路的连续作用, 可以用一序列冲击信号对电路激励去等效, 可以用一序列冲击信号对电路激励去等效,每个冲击信号
∞ ∞ ∞ ∞
∞
= ∫ f1(λ)[∫ f2(τ)] f3(t τ λ)dτ]dλ
∞ ∞
= f1(t)[ f2(t) f3(t)]
卷积的微分和积分: 二.卷积的微分和积分: 卷积的微分和积分 1.微分: 微分: 微分
d df2(t) df1(t) [ f1(t) f2(t)] = f1(t) = f2(t) dt dt dt
k=∞
yn (t) = ∑ f (kτ)τhn (t kτ) = ∑ f (kτ)hn (t kτ)τ
n=∞
和→积 分 当 (τ →0)时,τ → dτ, kτ → dτ , 求
任意信号:
f (t) = ∫ f (τ)δ(t τ)d τ
∞
∞
任意信号产生的零状态响应:
yzs (t) = ∫ f (τ)h(t τ)d τ
则有:
df1(t) t ∫ f2(λ)dλ y(t) = f1(t) f2(t) = ∞ dt
推论:
y (t) =[ f
(i)
( j) 1
(t) f
(i j) 2
(t)]
例:
dδ(t) t U(t)*U(t) = *∫ U(t)dt =δ(t)*tU(t) = tU(t) ∞ dt
三,与冲击函数或阶跃函数的卷积 1,与冲击函数的卷积:
∞ t
t
= f2(t)∫ f1(λ)dλ
∞
∫
t
∞
[ f1(λ)f2(λ)]dλ = ∫ [∫ f1(τ) f2(λ τ)dτ]dλ
∞ t ∞
t
t
= ∫ f1(τ)[∫ f2(λ τ)dλ]dτ
∞ ∞
t
= f1(t)∫ f1(λ)dλ
∞
t
3. 高阶导数和多重积分 设:
y(t) =[ f1(t) f2(t)]
1 ≤ t <1 2
t-2
t
0 h(t τ ) -1/2 1 t t (c) 1 ≤ t ≤ 3 f( τ ) h(τ )
τ
f( τ )
h(t τ )
f( τ )
h(t τ )
15/16 9/16 -1/2 0 1 3/2 2 (f) t
-1/2 0 t-2 1 (d)
t
t
τ
0 -1/2 1
t-2 t
5.4 电路系统对任意激励 的零状态响应- 的零状态响应-卷积积分
5.4.1 卷积积分定理: 卷积积分定理:
1.卷积积分定理:任一LTIS对任意激励信号 的零状态响应 卷积积分定理:任一 对任意激励信号f(t)的零状态响应 卷积积分定理 对任意激励信号 应该等于该激励信号与电路系统冲击响应的卷积积分. 应该等于该激励信号与电路系统冲击响应的卷积积分.即:
其余
f(t)
t<0 t>0
A 0 a
B
h(t)
Be-αt
0 t
t
(a)
f(t) A 0 a τ A 0
( b)
f(t)
(C)
( d)
a t
τ
(2)计算卷积积分:
y(t) = f (t)*h(t)
ⅰ.t<0, f (τ)和 (t τ) 无重叠. h ⅱ.0≤t≤a,tl1=0, tl2=-∞,选tr1=a, tr2=t
f (t)
R = 6
iL(t)
L= 2H
L diL(t) +iL(t) =δ(t) R dt R t R L ∴h(t) = e U(t) =3e3tU(t) L
(2)卷积求yzs(t) )卷积求y
τ iL(t) = ∫ f (t τ)h(τ)d = ∫ 2e(tτ ) 3 3τ dτ e
0 0
f (t)*δ(t) = f (t)
证明:
抽样性
f (t)δ(t) = ∫ f (τ)δ(t τ)dτ
∞ ∞
∞
= ∫ f (τ)δ(τ t)dτ
∞
1 t-2
1 -2 0 (c)
τ
0 t (d)
τ
(1)褶叠: (将横轴t→ (2)平移 (3)相乘积分
τ , h(τ) 对褶过去)
(2). 卷积积分积分限的确定原则: 若函数 f1( )和2(t τ) 的非零值左边界(即函数不为0的最小 的非零值左边界(即函数不为0 τ f 值)分别为t 值)分别为tl1和tl2,其非零值右边界(即最大的 τ 值)分别 积分下限取它们左边界的最大者,而积分上限取它们右边 界中的最小者.
为tr1和tr2,则积分下限为max[tl1,tl2],上限为min[tr1,tr2].即τ ,则积分下限为max[t ,上限为min[t
h(t τ )
t t-2
f(τ )
h(t τ )
f( τ )
f( τ )
-1/20 1 (a) ∞ < t ≤
1 2
τ
t
τ
t-2 -1/20 t 1 (b)
∞ ∞
τ t λ 令 =-
则 τ = λ t d = d λ -τ
∞ ∞
∴ f (t) = ∫ f2 (λ) f1(t λ)dλ = f2 (t) f) [ f2 (t) + f3 (t)] = f1(t) f2 (t) + f1(t) f3 (t)
f(t) A 0 a
B
h(t)
Be-αt
0 t
t
(a)
f(t) A 0 a τ A 0
( b)
f(t)
y(t) = ∫ f (τ)h(t τ)dτ
0
t
= ∫ ABe
0
t
α(tτ )
dτ =
AB
α
(1eαt )
(C)
( d)
a t
τ
ⅲ. t≥a ,tl1=0, tl2=-∞,tr1=a, tr2=t
τ
2. 利用卷积积分求电路系统零状态响应的方法: 利用卷积积分求电路系统零状态响应的方法: 方法步骤: 方法步骤: 求出系统的冲击响应h (1)求出系统的冲击响应h(t) 代公式进行卷积积分,或利用卷积性质,求得y (2)代公式进行卷积积分,或利用卷积性质,求得yzs(t) 例1:已知图示电路,(1)输入为 2etU(t) A电流,求响应 已知图示电路,( ,(1 电流, iL(t).(2)输入为 2e(t2)U(t 2) A电流,求响应i'L(t) .(2 电流,求响应i' 1.( 求得电路的冲击响应: 解: 1.(1)求得电路的冲击响应: 因为电路KCL: 因为电路KCL: KCL
证明:
d d [ f1(t) f2 (t)] = d t d t
∫
∞
∞
f1( ) f2 (t τ)d τ τ
d 2 (t τ) f = ∫ f1( ) τ d τ ∞ d t d 2 (t) f = f1(t) d t
∞
同理可证第二等式
2.积分 2.积分
∫
证明:
t
∞
[ f1(λ)f2(λ)]dλ = f1(t)∫ f2(λ)dλ
yzs (t) = yzs1(t) + yzs2(t) = (1e )U(t) (1e
t (t ) 1
)U(t 1 )
3.LTIS的完全响应: 利用卷积求得系统零状态响应,再与系统零输入响应叠加, 即求得系统的完全响应为: (设系统特征根互异)
y(t) = yzp(t) + yzs (t) = ∑A e + ∫ f ( )h(t τ)dτ τ zp
yzs (t) = ∫ f (τ)h(t τ)dτ = ∫ f (t τ)h(τ)dτ = f (t)h(t)
t0 t0
t
t
P n (t)
1 τ
h n (t )
LTIS
τ
δ(t) = lim P (t) n
τ → 0
证明:因为任意信号f(t)可以分解为宽度为 τ 的无穷多个窄脉 任意信号f 冲信号的迭加
λit
i= 1 0
n
t
4.卷积的图形解法 4.卷积的图形解法 (1). 卷积的图形解释: 卷积实际上是一种数学工具,我们可以用图解法来清楚的说 明其含义. h(t)h( τ )
f (t) → f (τ )
tr1 tτ
设:
ta1 -1/2 0 1 (a)
1 0 (b)
τ 2 t
h(τ )
h(t τ )
1
(d)
1 t2 t 3 f (t) h(t) = ∫ 1× (t τ)dτ = + + t2 2 4 2 4
1
(e)
f (t) h(t) = 0
例:求如图(a)(b)所说函数f(t)和h(t)的卷积积分. 解: (1)写出表达式:
A f (t) ={ 0 0 h(t) ={ αt Be
0 <t < a
3.结合律: 3.结合律: 结合律
[ f1(t) f2 (t)] f3 (t) = f1(t) [ f2 (t) f3 (t)]
