3.1-3.2 n维向量及其运算 向量组的相关性
合集下载
n维向量,向量间的线性关系
所以, R(1 ,2 ,3 , 1 ) 3, R(1 ,2 ,3 ) 2, 且 R(1 ,2 ,3 , 1 ) R(1 ,2 ,3 ) 故 1不能由向量组1 ,2 ,3线性表示.
例 设1 (1， 2， 1， 3)T ,2 (2,4, 2,6)T ,
其中 (2, 4,1, 1) , (1,5, 2,0)T .
T
解 因为
2 x 3 3 x
所以
x 3
3(2, 4,1, 1) (1,5, 2,0)T . (7, 17,1, 3)
T
T
§3.2 向量间的线性关系
3.2.1 线性组合与线性表示 3.2.2 线性相关与线性无关
a (a1 , a 2 ,, a n )
T
n 维向量写成一列，称为列向量，也就是列 矩阵，通常用 a , b, , 等表示，如：
a1 a2 a a n
分量全为零的向量
0,0,
,0 称为零向量。
定义 向量(a1 , a2 ,
(8)k k k
向量的运算律：
(9) 1 (10)k ( k 0) k (11)k 0 k 0或 0
注意：两个向量只有维数相同时，才能进行加 法和减法运算！
例 解向量方程
2 x 3 3 x
数乘向量：设 k 是一个数，向量
(ka1 , ka2 ,, kan )T
称为向量 a1 , a2 , 记为 k 向量的加法与数乘运算统称为向量的线性运算。 显然，向量的加法与数乘去处是矩阵的加法与数乘 运算的特例。因此向量的两种运算满足以下去处规 律。
, an 与数 k 的数量乘积。
n维向量的定义线性运算和线性相关性
x 1
AX
1 , 2
n
x2
xn
x 1 1
x 2 2
x n n
二、向量组的线性相关性
定义２ 对于向量组A: 1, 2, …, m, 如果存在一组不全为零的数k1,k2,…,km使关系式
k 11 k 22 .. k .mm 0
成立,则称向量组1, 2, …, m 线性相关.
例1：设有向量
1
1 4
2 2 3
1
0
n阶单位矩阵 I n 的n个列向量分别记为：
1
0
0
e 0 ,e 1 e
1 2
n 0
0
0
1
称为n维基本向量
第二节 n维向量的线性运算
定义1 设 (a 1 ,a 2 , ,a n )T , (b 1 ,b 2 , ,b n )T 是 n 维实
K是实数域中的一个数，则向量的加法
和数乘k向 分量 别定义
8 1 即数 1是数乘向量运算的单位 元
例1
1 ， 2 ， 3 ， 4 T 1 ， 2 ， 3 ， 4 T
(1) 求，的负向量
(2) 计算 43
第三节 向量组的线性相关性
一、线性组合
定义１:
给 定 向 量 组 A:{1， 2， L， m}， iRn,i1,2,L,m 对 任 何 一 组 实 数 k1,k2,L,km,称 k11k22Lkmm
例如 矩阵 A(aij)mn有n个m维列向量
aa 11
aa 22
aj
an
a11 a12 a1j a1n
Aa 21
a22 a2j a2n
am1 am2 amj amn
向a量 1,a 2 , 组 ,a n称为 A 的 矩 列 .阵 向
(完整版)第04讲(n维向量、向量组的线性相关性)
练习二答案
2 1 41
1、D4
r4 r1
3 1
1 2
2 3
1 2
3 1 2 1
2 1 41
r4 r2 3 1 2 1 0
1 2 32
0 0 00
2、
1
1
Dn 1 L
1
0 0L 1 a1 1 L
1 1 a2 L L LL 1 1L
0 1 1 L 1 an
c2 c1 c3 c1
cn1 c1
问 是否可由 1,2 线性表示？
解：设存在 k1, k2 使得
k11 k22
(3, 0, 4) k1(1, 0, 0) k2 (0, 0,1)
根据向量的运算法则，得，
43kk21
所以 是可由1,2 线性表示，且
31 42
注： 已知向量组 1,2 ,L ,m 和向量
判断向量 能否由向量组1,2 ,L ,m 线性表示
n(n1)
(1) 2
[(a i 1) (a j 1)]
n1i j1
n(n1)
(1) 2
( j i)
n1i j1
n!(n 1)! 2!1!
第二 章
n 维向量
4学时 一、n向量的概念、
向量组的线性相关性 二、线性相关性的判定、
向量组的秩
§2.1 n 维向量
一. n维向量的概念 二. n维向量的表示方法 三.向量的线性运算
全为零的数k1, k2 , , km使
k11 k2 2 km m 0
则称向量组A是线性相关的； 如果上式仅当k1=k2=…=km=0时才成立，则称 向量组A线性无关．
其中 , 是n维向量，, 是数。
线性方程组的向量表示
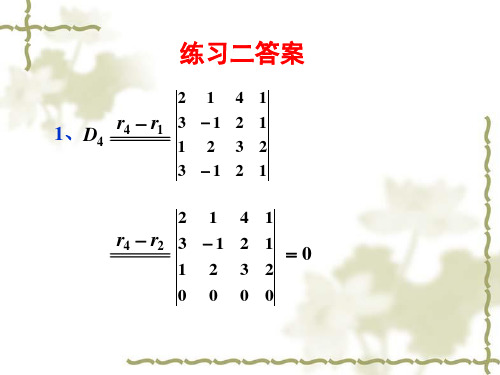
2 1 41
1、D4
r4 r1
3 1
1 2
2 3
1 2
3 1 2 1
2 1 41
r4 r2 3 1 2 1 0
1 2 32
0 0 00
2、
1
1
Dn 1 L
1
0 0L 1 a1 1 L
1 1 a2 L L LL 1 1L
0 1 1 L 1 an
c2 c1 c3 c1
cn1 c1
问 是否可由 1,2 线性表示？
解：设存在 k1, k2 使得
k11 k22
(3, 0, 4) k1(1, 0, 0) k2 (0, 0,1)
根据向量的运算法则，得，
43kk21
所以 是可由1,2 线性表示，且
31 42
注： 已知向量组 1,2 ,L ,m 和向量
判断向量 能否由向量组1,2 ,L ,m 线性表示
n(n1)
(1) 2
[(a i 1) (a j 1)]
n1i j1
n(n1)
(1) 2
( j i)
n1i j1
n!(n 1)! 2!1!
第二 章
n 维向量
4学时 一、n向量的概念、
向量组的线性相关性 二、线性相关性的判定、
向量组的秩
§2.1 n 维向量
一. n维向量的概念 二. n维向量的表示方法 三.向量的线性运算
全为零的数k1, k2 , , km使
k11 k2 2 km m 0
则称向量组A是线性相关的； 如果上式仅当k1=k2=…=km=0时才成立，则称 向量组A线性无关．
其中 , 是n维向量，, 是数。
线性方程组的向量表示
3-1,2n维向量及其运算向量组的线性相关性
0
1
定义2 设两个n维向量组
I
1, 2, 3,……,s
(II)
1, 2, 3, ……,t
如果(I)组中每一个向量i (i=1,2,…,s)都能由
向量组(II)线性表示，则称向量组(I)可以
由向量组(II)线性表示.
如果两个向量组可以相互线性表示，则称这
两个向量组等价.
例如，对于向量组
一. n维向量空间
1. n 维向量
定义：n 个有次序的数a1,a2 , ,an 所组成的有序数组
a1,a2 , ,an 称为一个n 维向量。
这 n 个数称为该向量的 n 个分量，第 i个数 ai 称为第 i 个分量。
分量全为实数的向量称为实向量，
分量为复数的向量称为复向量.
以后我们用小写希腊字母 , , 来代表向量。
注意 1. 若 1,2 ,
,
线性无关
m
,
则只有当
k1 km 0时, 才有
k11 k22 kmm 0成立 .
2. 对于任一向量组,不是线性无关就是
线性相关 .
的和，记为
负向量：向量 a1, a2 , , an 称为向量 的负向量
向量减法： ( )
数乘向量：设k为实数，向量 ka1, ka2 , , kan 称为向量 a1,a2 , ,an
与数k的数量乘积。记为 k
满足运算律：
(1)
(5)1
(2)( ) ( ) (6)k(l ) (kl)
例如：
(1,2,3,, n)
(1 2i,2 3i,,n (n 1))
第2个分量 第1个分量
第n个分量
n维实向量 n维复向量
向量通常写成一行： a1,a2 , ,an 称为行向量。
线性代数第3章 n维向量与线性方程组
29
例3.3.3判定向量组α1=（1，0，3，2），α2=（0， 1，4，3）的线性相关性. 定理3.3.6 如果向量组α1，α2，…，αs线性无 关，而β，α1，α2，…，αs线性相关，则β可 由α1，α2，…，αs线性表示，且表示式是惟一 的.
30
31
32
3.4 在实际问题中，一个向量组有时含有很多个 向量.对于一个线性相关的向量组，只要所含的向 量不全是零向量，就一定存在一部分向量，它们 是线性无关的.本节主要介绍向量组的最大线性无 关组和向量组的秩.
2
由n维向量加法与数乘运算的定义，不难证明， n维向量的线性运算满足下列运算规律：
3
例3.1.1 设
解
4
例3.1.2 将线性方程组
写成向量方程的形式.
5
解
令
6
即
7
3.2 3.2.1 向量的线性组合 定义3.2.1 例3.2.1 设有向量0=（0，0，0），α1=（1，-1， 2），α2=（3，5，6），α3=（-2，4，3），问： 向量0能否表为向量α1，α2，α3的线性组合？
8
例3.2.2 求证：任何一个n维向量 α=（a1,a2,…,an）都可由向量组
线性表示.
9
证明 因为
10
例3.2.3设β=（1，1，1），α1=（0，1，-1），α2= （1，1，0），α3=（1，0，2），问β能否由α1， α2，α3线性表示？若能，写出线性表示式. 解 设
11
12
3.2.2 向量组的线性相关性 定义3.2.2 例3.2.4 已知α1=（1，1，1），α2=（0，2，5）， α3=（2，4，7），试判定向量组α1，α2，α3的 线性相关性.
33
线性代数3-1
向量的线性运算满足的运算律： 向量的线性运算满足的运算律：
(1)α + β = β + α ; (2)(α + β ) + γ = α + ( β + γ ); (3)α + 0 = α ; (4)α + (−α ) = 0; (5)1 ⋅ α = α ; (6)k (lα ) = l (kα ) = (kl )α ; (7)k (α + β ) = kα + k β ; (8)(k + l )α = kα + lα .
骣1 ÷ a ç ÷ ç ÷ 的向量组a 1 , a 2 ,L , a m , 构成 ça 2 ÷ ç ÷ B= ç ÷ . çM ÷ 一个m´ n矩阵 ç ÷ ç ÷ ç ÷ ça ÷ ç m÷ 桫
m个n维行向量所组成
二、 向量的线性运算
设n维α = (a1 , a2 ,L , an ), β = (b1 , b2 ,L , bn ), k为实数,
向量、向量组与矩阵 向量、
若干个同维数的列(或行)向量所组成的集合 叫做向量组． 例如 矩阵A = (a ij )m n 有n个m 维列向量 ×
b1 b2
bj
a11 a12 L a1 j L a1n a 21 a 22 L a 2 j L a 2 n A= M M M M M M a a m 2 L a mj L a mn m1
= (a1 , 0,L , 0) + (0, a2 , 0,L , 0) + L + (0,L , 0, an )
= (a1 , a2 ,L , an ).
四、小结
维向量的概念； １． n 维向量的概念； ２．向量的线性运算； 向量的线性运算； ３．向量空间的概念。 向量空间的概念。
线性代数第三章第一节 n维向量及其线性相关(2014版)
有非零解，且它的一个非零解 的一组不全为零的系数。
8 0 k ( ) k k , 是 n维向量， k , l F
线性运算：上述向量的加法及数乘运算称为 向量的线性运算 注：
•满足上述 10 80 的运算称为线性运算。
(1) 0 0 (2) (1) ; (3)0 0. (4)如果k 0,则k 0或 0
(5)向量方程 x 有唯一解 x
V , V , 有 V ;
V ,k R, 有 k V .
定义： 设 V F n 的非空集合,如果对于 Fn 中的
加法及数乘两种运算封闭，那么就称集合V 为 F n 上
的向量子空间．
•两个特殊的子向量空间 V {o}和 F n 称为平凡子空间
例1：3维向量的全体 R3 是一个向量空间。
例2：V { ( x, y,0) | x, y R}
由xoy平面上所有向量全体构成的向量空间,是
R3 的一个子向量空间。
例3: 判别下列集合是否为向量空间.
(1)V1 x 0, x2, , xn T x2, , xn R
(2)V2 x 1, x2, , xn T x2, , xn R
示的一组不全为零的系数。
证：由向量组
1
,
2
,,
线性相关
m
存在一组不全为零实数k1, k2 ,, km ,
使
k11 k22 kmm 0
a11
a12
a1m 0
k1
a21
k2
a22
km
a 2 m
0
an1
an2
anm
0
以
1，
，
2
， m 为系数列向量的齐次线性方程组(*)
线性代数各章学习要点3
第3章n维向量和线性方程组向量是线性代数的重点内容之一，也是难点，对逻辑推理有较高的要求。
本章从研究向量的线性关系（线性组合、线性相关与线性无关）出发，然后讨论向量组含最多的线性无关向量的个数，即引出向量组的秩和最大无关组，最后，应用向量空间的理论研究线性方程组的解的结构。
无论是证明、判断、还是计算，关键在于深刻理解本章的基本概念，搞清楚其相互关系，并会灵活应用。
3. 1 n维向量及其运算定义（n维向量）由数域F中的n个数a-i,a2/ , a n组成的有序数组-■ - ( a i, a2, , a n)a2耳一称为数域F上的一个n维向量，前者称为行向量，后者称为列向量，其中a1, a2 / ,a n称为向量的分量（或坐标）。
分量是实（复）数的向量称为实（复）向量。
如果没有特殊的声明，以下所讨论指数域F上的向量。
行向量可以看成行矩阵，列向量看成列矩阵，向量的运算规定按矩阵的运算法则进行。
以下讨论的向量，再没有指明是行向量还是列向量时，都当作列向量。
设有向量■■ = （a i,a2,…，a n），- - （b1 ,b2 / , b n ）则向量相等的定义为- a i = b i （i=1,2,…,n）向量的加法定义为a + P =（a i +b i a? +b2 …a* +b n T数乘向量的定义为k：（「k）二（ka i,ka2, ,ka n）T向量的加法以及数乘运算统称为向量的线性运算，它满足下列8条运算规律（其中：■,'-,为n维向量，k,l为常数）：（1）二：+：= ：+=；)( :• - ) ( - )；(3)存在零向量0= ( 0,0，…，0 ) T，使得〉+0= ;(4)存在:-的负向量-二=(_a i,_a2,…，-a n)T,使得〉+ (-二)=0；(5)仁• = ：•；(6)k(l ： )=(kl):-;(7)k(: + 1 )=k +k :;(8)(k+l)用=k : +1 :;如果记矩阵A = (a j )m n的第j列向量为：a i ja2jQ j = : , (j=1,2,…,n)貝一则由向量的线性运算，可将方程组Ax=b写成下列形式：论一：* - X2J2…'x n J n二 b而齐次线性方程组A X=0则可写成向量形式：Xv 1 ■ X2： 2 …• X n： n = 03. 2向量组的线性相关性定义(线性组合)设宀，：^，…，〉m是一组n维向量，k1, k2/ ,k m是一组常数，则称向量kr 1 k2： 2 k m： m为向量〉1,〉2,i,〉m的一个线性组合，并称k1,k2 / , k m为该线性组合的系数。