多跨超静定梁的分布传递函数方法
同济大学结构力学第三章-2(多跨梁)

§3-2 多跨静定梁
(multi-span statically determinate beam)
附属部分--依赖 附属部分--依赖基本 依赖基本 部分的存在才维持几 何不变的部分。 何不变的部分。
组成 多跨 静定 梁的 部件
组 成 例 子
F1
F2
F2
F1
分析顺序:先附属部分,后基本部分。 分析顺序:先附属部分,后基本部分。 荷载仅在基本部分上,只基本部分受力, 荷载仅在基本部分上,只基本部分受力,附属 部分不受力; 部分不受力; 荷载在附属部分上,除附属部分受力外, 荷载在附属部分上,除附属部分受力外,基本 部分也受力。 部分也受力。
例
叠层关系图
先附属,后基本,区段叠加 先附属,后基本,
18 10 10 5 12
例
18
9 +
12 4 5 其他段仿 此计算 5 2.5 FN 图(kN) ) 9.5
9 q,各跨长度均为 , l。欲使梁上最大正、负弯矩的绝对值相等,试确 。欲使梁上最大正、负弯矩的绝对值相等, 定铰 B、E 的位置。 、 的位置。
由MC=AB跨中弯 跨中弯 矩可求得x 矩可求得
多跨 简支梁
作图示多跨静定梁的内力图,并求出各支座的反力。 例:作图示多跨静定梁的内力图,并求出各支座的反力。
1m
4m
4m
4m
1m
作图示多跨静定梁的内力图。 作图示多跨静定梁的内力图。
如何 求支座 B反力 反力? 反力
基本部分--不依赖其它 基本部分--不依赖其它 多跨静定梁实例 部分而能独立 部分而能独立地维持其 独立地维持其 几何不变性的部分。 几何不变性的部分。
建筑力学之 静定结构的内力分析知识详解

第二个脚标表示该截面所属杆件的另一端。例如 则表M示BA AB杆B端截面的弯矩。
表M示AB AB杆A端截面的弯矩,
❖ (3)内力图绘制
❖ 静定刚架内力图有弯矩图、剪力图、轴力图。刚架的内力图由各杆的内力图组合 而成,而各杆的内力图,只需求出杆端截面的内力后,即可按照梁内力图的绘制 方法画出。
❖ 6.平面刚架计算步骤
第十一章 静定结构的内力分析
❖ 第一节 楼梯斜梁和多跨静定梁 ❖ 1. 楼梯斜梁 ❖ 楼梯斜梁承受的荷载主要有两种,一种是沿
斜梁水平投影长度分布的荷载,如楼梯上人群 的重量等;另一种是沿倾斜的梁轴方向分布的 竖向荷载,如梁的自重等。 ❖ 一般在计算时,为计算简便可将沿梁轴方 向分布的竖向荷载按等值转换为沿水平方向分 布的竖向荷载,如图11-1 (a),沿梁轴线方向分 布 则的 由荷 于载 是等′值转转换换为,沿所水q 以平有方:向分布的荷q 载 ,
❖ (2)杆端内力的表示:如:FNAB 、 、 、 FNBA FQAB FQBA 、M AB 、M BA 等。 ❖ 注意:刚结点处不同方向有不同的杆端内力。
❖ 为了明确表示刚架上不同截面的内力,特别是为了区别汇交于同一结点的不同杆
端截面的内力,在内力符号右下角采用两个脚标;第一个脚标表示内力所属截面,
❖ 详解见教材
图11-21
❖ (6)结点法与截面法的联合应用 ❖ 欲求图11-23所示a杆的内力,如果只用结点法计算,不论取哪个结
点为隔离体,都有三个以上的未知力无法直接求解;如果只用截面法 计算,也需要解联立方程。 ❖ 为简化计算,可以先作Ⅰ-Ⅰ截面,如图所示,取右半部分为隔离 体,由于被截的四杆中,有三杆平行,故可先求1B杆的内力,然后以 B结点为隔离体,可较方便地求出3B杆的内力,再以3结点为隔离体, 即可求得a杆的内力。
多跨静定梁
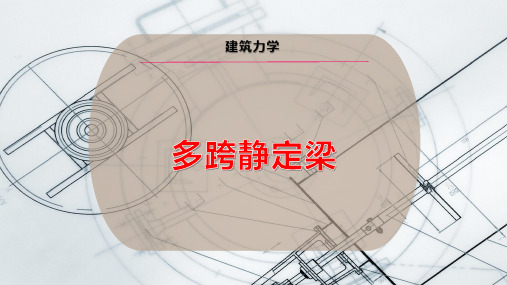
静定结构的内力\多跨静定梁 【例12.1】 试绘制图a所示多跨静定梁的内力图。 【解】 1)绘层次图。
如图b所示。 2)求支座反力。
FCx=0, FCy=-20kN, FDy=100kN , FAx=0 , FAy=48kN, FBy=12kN
3)绘内力图。各段梁 的约束反力求出后,可以 分别绘出各段梁的内力图。 如图(图d、e)所示。
目录
静定结构的内力\多跨静定梁 第二种如图b所示,其特点是第一跨无中间铰,其余各跨各有一
个中间铰。在图b中,AB梁是基本部分,而BC梁、CD梁则是附属部 分。图c为层次图。
目录
静定结构的内力\多跨静定梁
1.3 多跨静定梁的内力计算和内力图绘制
通过层次图可以看出力的传递过程。因为基本部分直接与基础 相连接,所以当荷载作用于基本部分时,仅基本部分受力,附属部 分不受力;当荷载作用于附属部分时,由于附属部分与基本部分相 连接,故基本部分也受力。因此,多跨静定梁的约束力计算顺序应 该是先计算附属部分,再计算基本部分。即从附属程度最高的部分 算起,求出附属部分的约束力后,将其反向加于基本部分即为基本 部分的荷载,再计算基本部分的约束力。当求出每一段梁的约束力 后,其内力计算和内力图的绘制就与单跨静定梁一样,最后将各段 梁的内力图连在一起即为多跨静定梁的内力图。
跨静定梁的承载能力大于系
列简支梁,在同荷载的情况
下可节省材料。
ห้องสมุดไป่ตู้
图2
目录
建筑力学
建筑力学
静定结构的内力\多跨静定梁
多跨静定梁
1.1 工程实例和计算简图
多跨静定梁是由单跨静定梁通过铰加以适当连接而成的结构。 如下面的公路桥梁和檩条梁。
目录
静定结构的内力\多跨静定梁
《静定多跨梁》课件

ONE
静定多跨梁
KEEP VIEW
REPORTING
CATALOGUE
目 录
• 静定多跨梁的基本概念 • 静定多跨梁的受力分析 • 静定多跨梁的强度与稳定性 • 静定多跨梁的设计与优化 • 静定多跨梁的施工与维护
PART 01
静定多跨梁的基本概念
定义与特性
定义
静定多跨梁是指在两个或多个支撑点 之间,由一根连续的梁所组成的结构 。
施工准备
在施工前,需要做好现场勘查 、设计图纸审核、材料采购等 工作,确保施工顺利进行。
梁体预制
在预制场或施工现场,按照设 计要求制作梁体,确保尺寸、 强度等符合规范要求。
附属设施安装
根据设计要求,安装栏杆、排 水设施等附属设施,提高桥梁 的安全性和使用功能。
静定多跨梁的维护与保养
日常检查
定期保养
建筑结构
在建筑结构中,静定多跨 梁可以作为楼面、屋面、 平台等的承重结构,提供 稳定和安全的支撑。
机械制造
在机械制造领域,静定多 跨梁可以作为机器部件的 支撑结构,如机床床身、 压力机框架等。
PART 02
静定多跨梁的受力分析
受力分析的基本原理
平衡原理
静定多跨梁在受力时,各 部分受到的力矩和力均达 到平衡状态。
特性
静定多跨梁具有稳定的结构特性,能 够承受多个方向的力和弯矩,且在受 力时不会发生变形或移动。
静定多跨梁的类型
根据支撑点的数量
静定多跨梁可分为双跨梁、三跨梁、 四跨梁等。
根据梁的形状
静定多跨梁可分为直线形梁、弧形梁 、折线形梁等。
静定多跨梁的应用场景
01
02
03
桥梁工程
分布传递函数方法的梁杆几何非线性分析

分布传递函数方法的梁杆几何非线性分析
李海阳;雷勇军;周建平
【期刊名称】《强度与环境》
【年(卷),期】2001(000)002
【摘要】本文提出了一种基于动坐标的、适用于梁大变形分析的传递函数方法.在本方法中,一个复杂系统被分为若干一维子系统,各子系统根据梁的有限变形理论进行推导.推导中把轴力看作子系统的参数,引入状态向量后,可以将子系统的控制方程改写为含参状态空间的形式,然后利用传递函数方法求解.系统的合成借鉴了有限元的处理方法,引入了动坐标关系,使方法可以用于对大变形的分析.文后给出的算例表明本文方法有很高的精度和很好的收敛性.
【总页数】7页(P12-18)
【作者】李海阳;雷勇军;周建平
【作者单位】国防科技大学航天与材料工程学院,;国防科技大学航天与材料工程学院,;国防科技大学航天与材料工程学院,
【正文语种】中文
【中图分类】O242
【相关文献】
1.分段轴压阶梯梁自由振动及稳定性分析的传递函数方法 [J], 李道奎;雷勇军;唐国金
2.多跨超静定梁的分布传递函数方法 [J], 蒋纯志;黄健全;唐政华
3.平面梁杆结构几何非线性分析的一种简便方法 [J], 王恒华;沈祖炎;陆瑞明
4.等截面铁木辛柯梁的分布传递函数方法 [J], 蒋纯志;金桂;陈亚琦
5.梁杆系统精确有限元方程及其在几何非线性分析和稳定计算中的应用 [J], 陆念力;张立强
因版权原因,仅展示原文概要,查看原文内容请购买。
04-讲义:3.3 多跨静定梁
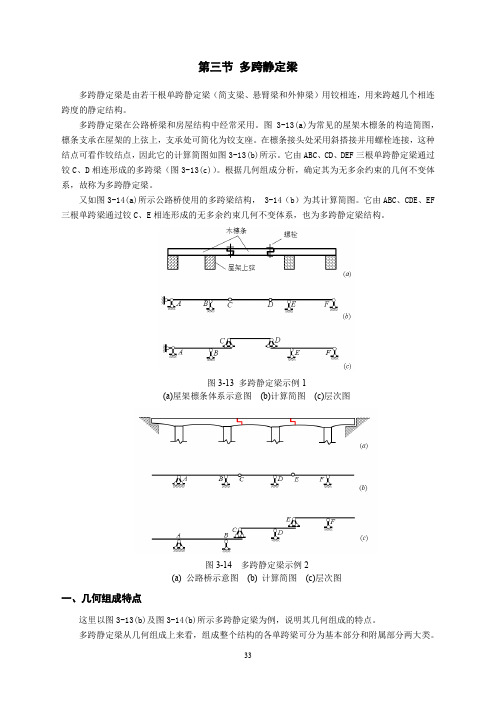
第三节多跨静定梁多跨静定梁是由若干根单跨静定梁(简支梁、悬臂梁和外伸梁)用铰相连,用来跨越几个相连跨度的静定结构。
多跨静定梁在公路桥梁和房屋结构中经常采用。
图3-13(a)为常见的屋架木檩条的构造简图,檩条支承在屋架的上弦上,支承处可简化为铰支座。
在檩条接头处采用斜搭接并用螺栓连接,这种结点可看作铰结点,因此它的计算简图如图3-13(b)所示。
它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁(图3-13(c))。
根据几何组成分析,确定其为无多余约束的几何不变体系,故称为多跨静定梁。
又如图3-14(a)所示公路桥使用的多跨梁结构, 3-14(b)为其计算简图。
它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系,也为多跨静定梁结构。
图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例,说明其几何组成的特点。
多跨静定梁从几何组成上来看,组成整个结构的各单跨梁可分为基本部分和附属部分两大类。
基本部分是指本身能独立维持平衡的部分,而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。
因此,多跨静定梁从几何组成上来看见,是先固定基本部分,再固定附属部分。
如图3-13(b)中多跨静定梁,梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础,它不依赖于其他部分就能独立维持自身的几何不变性;梁段DEF 虽然只有两根链杆与基础相连,但在竖向荷载作用下自身也能维持平衡。
因此,梁段ABC 、梁段DEF 均为基本部分。
而梁段CD 支承于前述两个基本部分上,它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变,所以是附属部分。
为了更清楚地表明多跨静定梁中各梁段之间的支承关系,常把基本部分画在附属部分的下方,附属部分画在基本部分的上方,如图3-13(c)所示,称为层次图。
§3-2多跨静定梁
F -0.25 -0.25
0.5 0.5 -0.25 -0.25
Step3:绘制内力图。
FPa
D A B C
0.25 Pa F
E F
0.5FP
A B C D E F
0.5FPa
0.25FP
FP
M图
FQ图
【例3.3 】
试求铰D的位置,使负弯矩峰值与正弯矩峰值相等
q
A
q
B C A D B
q
C
l−x
D
x
§3-2 静定多跨梁
一、定义及常用形式
多跨静定梁:由若干根梁用铰连接而成、用来跨越几个相连跨度的静定梁。
无铰跨和两铰跨交替 出现
除第一跨外,其余各 跨皆有一铰
前两种方式组合
二、几何构造特点及受力特点
主梁或基本部分 1、几何组成 次梁或附属部分 不依赖其它部分的存在,本身就 能独立地承受荷载并能维持平衡 的部分 需要依赖其它部分的支承才可以 承受荷载并保持平衡的部分
FRC
D E F RE F
∑Y = 0
对EF部分:
M RF FRD
FRD = −0.75 FP
FRB
FRF
∑ M E = 0 M RF = 0.25FP a FRF = 0.25 FP ∑Y = 0
FP
A B C
0.5FP
D E
FP
0.25 FP
F A B C D
0.25FP a
E F
1.5FP
0.75FP
FRB
FRC
q (l − x) 2 q (l − x) x qx 2 M 跨中 = ,M B = + 8 2 2
得:
M 跨中 = M B
《超静定梁》PPT课件
B
8 Fa 9 - 2021/4/23
FN' wBB2
1F 9 B
wB1 wB2
C
查表得:
wB1
(F
FN 3EI
)a3
C
wB 2
FN (2a)3 3EI
代入上式得:FN
FN
1 9
F
C
弯矩图为:
2
-
Fa 9
21
四、超静定结构(梁)的其它解法及研究现状
将未知问题转化为 已知问题,通过消除已 知问题和原问题的差别, 使未知问题得以解决。
2021/4/23
16
么么么么方面
• Sds绝对是假的
方法二 取支座 A 处阻止梁转动的约束 为多余约束。 代之以与其相应的多余反力偶 MA 得基本静定系。
变形相容条件为:
A 0
2021/4/23
q
B
A l
MA
q
B A
l
基本静定系
18
MAqΒιβλιοθήκη 变形相容条件为: A 0 B
几何方程
A
Aq AMA 0
郑州大学的李会知教授分析了集中荷载或均布荷载作用下 两端固支梁和一次超静定梁的弹塑性加载及变形过程,并 给出了加载各阶段的弯矩和位移计算公式。
中南大学的陈玉骥副教授采用半逆解法,求出了一端固定 一端铰支单跨超静定梁在均布荷载作用下的应力和位移, 并由此说明了材料力学解的精度和适用性。
燕山大学的韩晓娟副教授在三弯矩方程应用中引入刚度系 数和载荷分布系数,使应用这一定理解决工程实际问题时 更简捷、方便和实用.
2021/4/23
9
三 、变形比较法解超静定梁
图示为抗弯刚度为 EI 的一次超静定梁。 变形比较法: (1)将可动铰链支座B
材料力学练习2
填空弯曲内力图1、在静定多跨梁中,如果中间铰点处没有外力偶,那么不变,恒等于零;答案剪力、弯矩答疑中间铰只传递剪力,不传递弯矩。
当中间铰处没有外力偶作用时,中间铰处的弯矩恒等于零,剪力图没有变化。
2、简支梁的受力如图,为使梁的中点的截面处的弯矩为零,那么外力偶m=。
答案 m=qL2/4答疑对A点取矩,得到B处的约束反力为N B=M/L+ql/2中间截面处的弯矩为: M(L/2)=N B×L/2-M-qL/2×L/4整理得到:M(L/2)=(M/L+qL/2)×L/2-M-ql2/8=-M/2 + qL2/8考虑到已知条件有M(L/2)=0 得到外力偶的大小为: M=qL2/43、图示中的四个梁的跨度、材料、截面、载荷均相同,比较各梁的最大弯矩值(绝对值),其中最大的在梁上。
答案最大弯矩发生在C 梁上答疑 a图中的最大弯矩为qL2/8;b图中的最大弯矩为qL2/40;c 图中的最大弯矩为qL2/2;d图中的梁为一次静不定,与图c相比,梁的弯曲变形较小,中性层处的曲率较小,根据1/ρ=M(x)/EI可知,d图中的最大弯矩偏小选择梁的合理受力1、工人工作在木板的中点,为改善木板的受力,下列做法哪一个好?A:在A、B处同时堆放适量砖; B:在A、B端同时堆放砖块,越多越好;C:只在A或只在B处堆放适量砖; D:什么也不放。
答案正确选择 A答疑木板的受力合理的状态是最大正弯矩和最大负弯矩的绝对值相等。
只有在A、B两处同时堆放适量砖的情况下,C、D两截面处产生最大负弯矩,且要求最大负弯矩的数值相等。
但是堆放的砖不是越多越好,应该保证在C、D截面处的最大负弯矩与木板的中间截面处产生的最大正弯矩的绝对值相等,此时木板的受力最合理。
填空梁的合理受力1、图示木板,受力为P、梁的总长为L、外伸部分长为a,使梁的最大弯矩为最小时,梁端的重物Q=。
答案 Q= P(L-2a)/8a答疑当梁的最大正弯矩与最大负弯矩的绝对值相等时,梁的最大弯矩为最小。
材料力学习题集 (有答案)
绪 论一、 是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
( ) 1.2 内力只能是力。
( )1.3 若物体各点均无位移,则该物体必定无变形。
( ) 1.4 截面法是分析应力的基本方法。
( ) 二、选择题1.5 构件的强度是指( ),刚度是指( ),稳定性是指( )。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力 B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是( ) A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力参考答案:1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆CD 位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q ,杆CD 的横截面面积为A ,质量密度为ρ,试问下列结论中哪一个是正确的? (A) q gA ρ=;(B) 杆内最大轴力N max F ql =; (C) 杆内各横截面上的轴力N 2gAlF ρ=;(D) 杆内各横截面上的轴力N 0F =。
2. 低碳钢试样拉伸时,横截面上的应力公式N F A σ=适用于以下哪一种情况? (A) 只适用于σ≤p σ; (B) 只适用于σ≤e σ; (C)3. 在A 和B和点B 的距离保持不变,绳索的许用拉应力为[]σ取何值时,绳索的用料最省? (A) 0; (B) 30; (C) 45; (D) 60。
4. 桁架如图示,载荷F 可在横梁(刚性杆)DE 为A ,许用应力均为[]σ(拉和压相同)。
求载荷F 的许用值。
以下四种答案中哪一种是正确的?(A)[]2A σ; (B) 2[]3Aσ;(C) []A σ; (D) 2[]A σ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:2017-10-13基金项目:湖南省教育厅科研基金项目(14C1060);郴州市科技计划项目(CZ2014042)作者简介:蒋纯志(1967 ),女,湖南永州人,教授,研究方向:计算结构力学,非均质材料位错理论.多跨超静定梁的分布传递函数方法蒋纯志,黄健全,唐政华(湘南学院电子信息与电气工程学院,湖南郴州 423000)摘 要:为了求解多跨超静定梁的静力学响应,提出了多跨超静定梁静力学分析的分布参数传递函数方法.通过定义状态变量,把挠曲线微分方程改写成状态空间形式的基本控制方程,并借助有限元法的单元组集方式,建立了适用于复杂荷载和边界条件的多跨超静定梁传递函数求解模型.该模型可计算超静定梁各截面的内力和变形.最后给出一个算例验证此方法的准确性和有效性.关键词:超静定梁;静力学;传递函数方法;变形;内力中图分类号:O342 文献标识码:A DOI :10.3969/j.issn.1672-8173.2018.02.0061 引言在工程中由于构造上的需要,或者为了提高梁的刚度与强度,往往需要给静定梁再增加约束,使得静定梁成为超静定梁.通常超静定梁的求解方法是解除多余约束,使超静定梁变为静定梁,利用静力平衡方程和变形协调方程计算出支反力,继而做出梁的弯矩图.通过积分法或者叠加法进行变形计算.计算过程冗长繁琐,十分不方便,尤其对于多跨超静定梁求解更是困难.因此,人们一直在探索新的计算方法来简化超静定梁的变形计算,诸如叠加法[1]㊁直写法[2]㊁等直梁的置换法[3]㊁分段独立一体化积分法[4]等.这些方法各有其特点和针对性.分布传递函数方法是基于控制论和半解析有限元思想的一种新的计算方法,近十几年来,经过一些学者的研究和应用,此方法在力学领域取得了较好的进展[5-7].这种方法具有求解精度高㊁易于编程实现等优势.本文将传递函数方法引入到多跨超静定梁的内力和变形计算,通过定义状态变量,把梁的挠曲线微分方程改写成状态空间形式的基本控制方程,借助有限元法的单元组集方式,建立适用于各种复杂荷载超静定梁的传递函数求解模型,利用计算机编程运用可以较简单有效地对多跨超静定梁进行分析计算.2 单元分布传递函数方程首先将多跨超静定梁按其荷载㊁支座分成若干单元,任取一单元分析.在单元上建立坐标系,x ∈[-a ,a ],单元的长度设为2a .梁的挠曲线微分方程EI d 4w dx 4=q (x ).(1)定义状态变量η(x )=w (x ) dw (x )dx d 2w (x )dx 2 d 3w (x )dx []3T .将挠曲线微分方程改写成状态空间形式的基本控制方程d dxη(x )=Fη(x )+g(x ).(2)定义节点位移向量r =w (-a ) dw (-a )dx w (a ) dw (a )dx [] T .边界条件表示为Mη(-a )+Nη(a )=r .(3)㊃92㊃2018年4月第39卷第2期 湘南学院学报Journal of Xiangnan University Apr.,2018Vol.39No.2通过传递函数法,得到满足边界条件(3)的方程(2)的解:η(x )=H(x )r +f(x ).(4)其中H (x )=e Fx [Me -Fa +Ne Fa ]-1,(5)f (x )=∫a -a G(x ,ξ)g(ξ)dξ,G (x ,ξ)=H (x )Me F (-a -ξ)ξ<x -H (x )Ne F(a -ξ)ξ{>x.(6)若是单跨超静定梁,就可以依据边界条件和荷载情况直接得出梁各点的挠度和转角,继而求出各点内力.3 多跨超静定梁的组集方法对于多跨超静定梁,利用传递函数方法对每个单元求解,通过单元间连接点上的广义力平衡条件,将所有子系统组装在一起,形成总体平衡方程,根据梁的荷载情况,即可获得整个梁的传递函数解.首先定义广义力向量σ(x )=Q (x )M (x éëêêùûúú).(7)由材料力学的本构关系,广义力为σ(x )=E ηη(x ).综合式(1)㊁(6)和(7)得出本构矩阵E η=0 0 0 EI 0 0 EI éëêêùûúú 0.利用(7)联立推导单元两端节点的广义力为σ=σ(-a )σ(a éëêêùûúú)=E ηH (-a )-E ηH (a éëêêùûúú)r +E ηf (-a )-E ηf (a éëêêùûúú)=kr +v .(8)考虑单元的节点外力,得到本单元的节点平衡方程s =kr +v .(9)其中s 为单元节点集中外力向量㊂借助有限元的单元组集方式对各单元组集,得到复杂系统的节点平衡方程:S =KR +V .S 是梁上外力向量,由s 构成;K 和V 分别由k 和v 组集而成.引入边界条件,对边界条件的处理方式与有限元相同.根据(9)式求得梁上各单元节点的位移R ,代入(4)式,便能求出超静定梁上各点的挠度和转角,继而计算出各点的内力值.4 算例下图连续梁,有4个等长跨度,弯曲刚度EI 为常数.在第三跨加均布荷载图1 载荷图Fig.1 Load diagram将整个梁分成四个单元,分别是AB㊁BC㊁CD㊁DE,任取一单元,依照上述方法建立传递函数方程.分析梁的载荷和约束情况,外力向量为S =[0 0 0 0 0 0 0 0 0 0]T .取EI㊁q ㊁l 均为1,用MATLAB 编程运算,并绘制弯矩图㊁挠度图和转角图.5 结论研究了分布传递函数方法对于多跨超静定梁的适用性,得到一种求解多跨超静定梁的新的计算方法.这㊃03㊃湘南学院学报(自然科学版) 2018年4月(第39卷)第2期种方法形式规范统一,便于计算机编程和操作,适合于任意的边界条件和复杂外力情况.算例利用本方法分析了四跨连续超静定梁,画出了剪力图㊁弯矩图㊁转角图和挠度图,其结果与文献4相同.分布传递函数方法使用起来灵活㊁高效,可应用的领域非常广泛,是一种对各种结构进行处理的行之有效的方法. 图2 剪力图 图3 弯矩图 Fig.2 Shear force diagram Fig.3Bending moment diagram 图4 转角图 图5 挠度图 Fig.4 Angle of rotation diagram Fig.5 Deflection diagram参考文献:[1]刘鸿文.材料力学[M].北京:高等教育出版社,2011.[2]孙仙山,张方春. 直写法”求解静不定连续梁[J].山东工业大学学报,1999,2:197-200.[3]喻晓今.求超静定等直梁的置换法[J].工程力学,2007,24(6):66-69.[4]吴艳艳,李银山,魏剑伟,李彤.求解超静定梁的分段独立一体化积分法[J].工程力学,2013,30(6):11-14.[5]SHEN Zhibin,SHENG Liping,LI Xianfang,TANG Guojin.Nonlocal Timoshenko beam theory for vibration of carbon nanotube-based biosensor[J].Physica E,2012,44:1169-1175.[6]SHEN Zhibin,LI Daokui,LI Dong,TANG Guojin.Frequency shift of a nanomechanical sensor carrying a nanoparticle using nonlo⁃cal Timoshenko beam theory[J].Journal of Mechanical Science and Technology,2012,26:1-8.[7]蒋纯志,金桂,陈亚琦.传递函数方法在复杂曲梁计算中的应用[J].机械设计与制造,2011,7:84-86.(下转第120页)㊃13㊃蒋纯志,等:多跨超静定梁的分布传递函数方法湘南学院学报(自然科学版) 2018年4月(第39卷)第2期Study on Pricing of Take-Photos-to-Make-MoneyCrowdsourcing PlatformLIU Wenhao1,SUN Jiaqian1,XING Yao1,LIU Zhigang2(1.College of Business Administration,Northeastern University,Shenyang110004,China;2.College of Mathematics and Finance,Xiangnan University,Chenzhou423000,China)Abstract:The pricing problem of Take-Photos-to-Make-Money Crowdsourcing Platform is studied.By u⁃sing the influence diffusion function and MATLAB software,the multiple linear regression model of the pri⁃cing problem of camera making money making task is pared with the original problem,our model has lower cost and higher task completion rate.opportunity costKey words:influence diffusion model,K-Means cluster analysis,(上接第31页)Distributed Transfer Function Method for Multi SpanStatically Indeterminate BeamJIANG Chunzhi,HUANG Jianquan,TANG Zhenghua(College of Electronic Information and Electronic Engineering,XiangnanUniversity,Chenzhou423000,China)Abstract:To solve the static response of multi-span statically indeterminate beam,a distributed transfer function method is presented.By defining the state variables,the differential equation of the deflection curve is rewritten as the basic control equations in state space form.And with the aid of the unit set mode of finite element method,a solution modelof multi-span statically indeterminate beam transfer function,which is ap⁃plicable to various kinds of complicate external forces and boundary,is established.Moreover,the model can be used to calculate the internal force and deformation.An example is given to verify the accuracy and effectiveness of this method.Key words:statically indeterminate beam,statics,transfer function method,deformation,internal force㊃021㊃。
