14.4 单跨超静定梁的极限荷载
结构力学专题十六(单跨梁极限荷载计算)

P
P
A
D
B
C
l/3 l/3 l/3
共有三种可能的破坏机构
Fpu
4 l
Mu
F1
5 l
Mu
F2
4 l
Mu
2.用试算法求解
F3
9 l
Mu
作业:
16—3、 16—4。
补:求图示结构的极限荷载, 材料极限弯矩为Mu。
M
A
C
B
3m
1m
(2)平衡弯矩法
Mmax 1.5FPu M u
FPu
2 3
Mu
2F
F
2m
2m
1m
小结: 静定梁极限荷载计算特点:
静定结构无多余约束,出现一个塑性铰即成为破 坏机构。这时结构上的荷载即为极限荷载。
塑性铰出现的位置应为截面弯矩与极限弯矩之比 的绝对值最大的截面。
求出塑性铰发生的截面后,令该截面的弯矩等于 极限弯矩,利用平衡条件即可求出极限荷载。
(1)可破坏荷载 Fp
对任一破坏机构,由平衡条件求出的荷载称为可破坏 荷载;
(2)可接受荷载 Fp
同时满足屈服条件和平衡条件的荷载称为可接受荷载;
(3)极限荷载 Fpu
同时满足三个条件的荷载称为极限荷载,即极限荷载 既是可破坏荷载,又是可接受荷载。
4、一般定理
(1)基本定理(预备定理)
可破坏荷载恒不小于可接受荷载 Fp Fp
第十六章 梁和刚架的极限荷载
§16-3 单跨梁极限荷载计算
一、静定梁 例2:求图示结构的极限荷载,
材料极限弯矩为Mu。 (1)机动法
2F
F
2m
2m
1m
塑性铰出现在支座处
结构力学第17章结构的塑性分析与极限荷载

Mu
(
l
) 0
l
得:
FPu
6M u l
[例] 求梁的极限荷载,已知极限弯矩为Mu。
q
qu
A
C
B
l/2
l/2
A Mu
Mu l
C B
2 Mu
解:计算刚体虚功:
2
瞬变体系机构
W
l
y qu dx
Mu
Mu
Mu
qu
(
l
l
)
M u
qu l
M u
虚功方程:
qu l
M u
qu
16M u l2
FPu
M
' u
3 2l
Mu
9 2l
A
M ' u
A
2l /3
FPu
DC
Mu
D
l/3
FPu
l
(M u
M u )
A
3 2l
D
3 2l
3 l
9 2l
弯矩图如图,弯矩
MB=
1 2
(M
' u
Mu )
M
u
,即M
' u
3M u
时,此破坏形态就可实现。
M' u
1 2
(M
' u
-
M
u
)
FPu D
C
A
B
Mu
综上,当M
Mu
FP增大
A
C
B
FP继续增大,第二个塑性铰出现在C 截面,梁变为机构。弯矩 增量图相应于简支梁的弯矩图(如图)。
Mu
FP达到极限值FPu
梁的极限荷载

2M u A
B
Mu
B
A
1 L
B
1 0.5L
21 L
表示B截面左侧转角。代入后整理得
qu
20M u 3L2
---------------------------(1)
θA Δ1 θB-
Mu Δ2
Mu
A
Δ3 D
2Mu
B
Mu
C
Mu
2Mu
第二跨:2
q
A
B
L
解:①当荷载q≤qy时,梁处于弹性阶段,作出如下的弯矩图,
并求得最大正弯矩发生在离B端 处3,L Mmax=
8
qL2 14.22
qL2/8
qL2/14.22 3L/8
②随着荷载的增加,A截面首先出现塑性铰。若荷载继续增加, 梁变为简支梁。增加的荷载由简支梁承担。
Mu
Mu
③由于增加的荷载由简支梁承担,最大正弯矩的位置将发生 变化。设第二个塑性铰的位置距离B端 x 处
L/2
弹性阶段
M PL 4
PyL/4
L/2
L/2
弹性极限阶段
My
Py L 4
静力法求极限荷载 Pu
Mu
L/2
L/2
极限荷载阶段
Mu
Pu L 4
Pu
4M u L
虚位移法求极限荷载 Pu
θ L/2
Mu
θ L/2
极限荷载阶段
Pu 2M u
L
2 L
2
Pu
2M u
4M u L
结构力学极限荷载

结构力学(2)
浙大宁波理工学院土建学院
2)虚功法(作破坏机构图)
FP
红线为变形后的杆件,兰点为塑性铰
A
C
Mu
1
Mu
2
1B1源自l/22l
2
21
4
l
令机构产生虚位移,使C截面竖向
位移和荷载FP同向,大小为δ
外力虚功: We FP
内力虚功:
Wi
M u1
Mu2
2
Mu( l
4
l
)
6Mu
l
由
We=Wi 得: FPu
Fpu
=
(a+b)M ab
u
2Fp Fp
l/2
l/2
7 Fpl 16
5 Fpl 8
M图
5 M max 8 Fpl M u
Fpu
=
8M 5l
u
M max 2Fpl M u
Fpu
=
Mu 2l
结构力学(2)
浙大宁波理工学院土建学院
例 求静定梁的比例加载时的极限荷载Fpu
2Fp Fp
弯矩图法
A
3Mu
极限荷载(P266)
结构破坏时所能承担的的荷载。
结构力学(2)
浙大宁波理工学院土建学院
§17-2 极限弯矩、塑性铰、极限荷载 、极限状态
基本假设(一般针对钢材料) 1、材料为“理想弹塑性材料” 。 2、材料均匀,各向同性。 3、平面假定。即无论弹、塑性阶段,都保持平截面不变。
s A
塑性流动状态
C
o
C Mu
B Mu D
l
l/2
l/2
Fpl
解:作弯矩图
A
结构力学极限荷载

Harbin Institute of Technology超静定梁中的极限荷载的研究课程名称:结构力学院系:土木工程学院班级:1433111姓名:李渊学号: 1143310120摘要:大多数工程材料,特别是钢材,受力后发生变形,一般都存在线性弹性阶段、屈服阶段和强化阶段。
因此,随着荷载的增加,结构截面上应力大的点首先达到屈服强度,发生屈服,结构将进入弹塑性状态。
这时虽然截面部分材料已进入塑性状态,但尚有相当大的部分材料仍处于弹性范围,因而结构仍可继续加载。
当荷载增加到一定程度,结构中进入塑形的部分不断扩展直至完全丧失承载能力,导致结构崩溃(或倒塌)。
因此研究结构极限状态下的极限荷载,是十分有必要的,对于结构安全储备的考虑的依据提供有重要意义。
正文:一、极限荷载的有关意义定义:结构出现塑性变形直到崩溃时所能承受的最大荷载,称为极限荷载,它是考虑结构安全储备设计依据的因素之一,且按极限状态设计结构比弹性设计更经济。
通过对弹性设计方法及其许用应力设计法的研究,并在其方面进行了探讨,得到弹性设计方法及其许用应力设计法的最大缺陷是以某一截面上的max σ达到[σ]作为衡量整个结构破坏的标准。
事实上,由塑性材料组成的结构(特别是超静定结构)当某一局部的max σ达到了屈服应力时,结构还没有破坏,还能承受更大的荷载。
因此弹性设计法不能充分的利用结构的承载能力,是不够经济的。
塑性分析考虑了材料的塑性性质,其强度要求以结构破坏时的荷载作为标准:max []PuP p uF F F k ≤=其中,Pu F 是结构破坏时荷载的极限值,即极限荷载。
u k 是相应的安全系数。
对结构进行塑性分析时仍然要用到平衡条件、几何条件、平截面假定,这与弹性分析时相同。
另外还要采用以下假设:图1(1)材料为理想弹塑性材料。
其应力与应变关系如图所示。
(图1)(2)比例加载:全部荷载可以用一个荷载参数P 表示,不会出现卸载现象。
(3)结构的弹性变形和塑性变形都很小。
14.6 比例加载时判定极限荷载的一般定理

14.6.5 四个定理
FP+ 恒不小于可接受荷载 FP− 基本定理: 基本定理:可破坏荷载
FP+ ≥ FP−
【证明】1) 取任一可破坏荷载对于相应的单向机构的 证明】 虚位移, 虚位移,可列出虚功方程 n n FP+ ∆ = ∑ M uiθ i = ∑ M ui θ i
A
1.2 FP3 Mu D
+
待定部分
1.5Mu
Mu A
B E FP3
+
D l /2
Mu
C
C
Mu
梁的其他部分均不会超出相应的极 限弯矩。因此,满足内力局限条件。 限弯矩。因此,满足内力局限条件。
+ 1.2 FPu
1.2 FP3
1.5Mu
+
3 Mu l
Mu A D
0.27Mu B E FPu
+
Mu
C
D
4 Mu l
All Rights Reserved 重庆大学土木工程学院®
+
+ +
【例14-6】试用极小定理求图示单跨超静定梁,在均布荷 】试用极小定理求图示单跨超静定梁, 载作用下的极限荷载值。 载作用下的极限荷载值。 可对图示的可能位移列出虚功方程
q+
∆
l−x
q A EI =常数 l B
l∆ = Mu (θA + θC ) 2
1.5Mu C FP3
1.5Mu E l /2
4 Mu l 3 Mu l
+
验算内力局限条件
+ 3M u l M B = FP3 − − 1.5M u = −0.27 M u l 2
国家开放大学电大《力学》题库
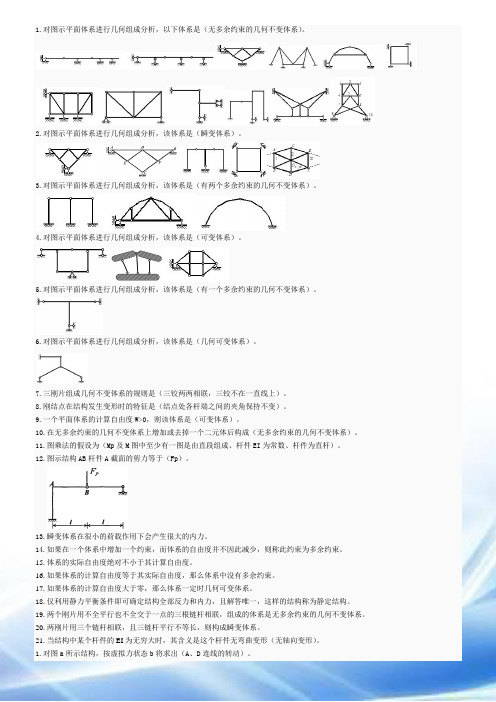
1.对图示平面体系进行几何组成分析,以下体系是(无多余约束的几何不变体系)。
2.对图示平面体系进行几何组成分析,该体系是(瞬变体系)。
3.对图示平面体系进行几何组成分析,该体系是(有两个多余约束的几何不变体系)。
4.对图示平面体系进行几何组成分析,该体系是(可变体系)。
5.对图示平面体系进行几何组成分析,该体系是(有一个多余约束的几何不变体系)。
6.对图示平面体系进行几何组成分析,该体系是(几何可变体系)。
7.三刚片组成几何不变体系的规则是(三铰两两相联,三铰不在一直线上)。
8.刚结点在结构发生变形时的特征是(结点处各杆端之间的夹角保持不变)。
9.一个平面体系的计算自由度W>0,则该体系是(可变体系)。
10.在无多余约束的几何不变体系上增加或去掉一个二元体后构成(无多余约束的几何不变体系)。
11.图乘法的假设为(Mp及M图中至少有一图是由直段组成、杆件EI为常数、杆件为直杆)。
12.图示结构AB杆件A截面的剪力等于(Fp)。
13.瞬变体系在很小的荷载作用下会产生很大的内力。
14.如果在一个体系中增加一个约束,而体系的自由度并不因此减少,则称此约束为多余约束。
15.体系的实际自由度绝对不小于其计算自由度。
16.如果体系的计算自由度等于其实际自由度,那么体系中没有多余约束。
17.如果体系的计算自由度大于零,那么体系一定时几何可变体系。
18.仅利用静力平衡条件即可确定结构全部反力和内力,且解答唯一,这样的结构称为静定结构。
19.两个刚片用不全平行也不全交于一点的三根链杆相联,组成的体系是无多余约束的几何不变体系。
20.两刚片用三个链杆相联,且三链杆平行不等长,则构成瞬变体系。
21.当结构中某个杆件的EI为无穷大时,其含义是这个杆件无弯曲变形(无轴向变形)。
1.对图a所示结构,按虚拟力状态b将求出(A、D连线的转动)。
2.图示虚拟状态是为了求(A截面转角)。
3.图示为刚架的虚设力状态,按此力状态及位移计算公式可求出()。
李廉锟《结构力学》(下册)笔记和课后习题(含考研真题)详解(结构的极限荷载)

第14章 结构的极限荷载14.1 复习笔记【知识框架】结构分析方法 弹性分析方法 塑性分析方法的基本概念 塑性分析方法 塑性分析中力学性能的简化 塑性分析的注意事项塑性铰 塑性铰的定义 塑性铰与普通铰的区别 极限弯矩、塑性铰、破坏机构与静定梁的计算 极限弯矩的定义及求法 破坏机构超静定梁的特点 静定梁的极限荷载计算 单跨超静定梁的极限荷载 静力法求极限荷载极限荷载的计算 机动法求极限荷载 比例加载的定义 机构条件 结构处于极限状态时满足的条件 内力局限条件 比例加载时有关极限荷载的几个定理 破坏荷载与接受荷载 平衡条件 极小定理 比例加载时有关极限荷载的几个定理 极大定理结构的极限荷载穷举法的描述唯一性定理计算极限荷载的穷举法和试算法试算法的描述穷举法的计算步骤试算法的计算步骤连续梁的可能破坏机构形式连续梁的极限荷载计算方法连续梁的极限荷载的计算计算步骤刚架的可能破坏机构形式刚架的极限荷载计算方法刚架的极限荷载的计算计算步骤矩阵位移法求刚架极限荷载的概念【重点难点归纳】一、塑性分析方法的基本概念1.结构分析方法(1)弹性分析方法①定义弹性分析方法是指以结构在弹性阶段的最大应力达到极限应力作为结构破坏的标志的结构分析方法,又称为许用应力法。
②强度条件式中,σmax为结构的实际最大应力;[σ]为材料的许用应力;σu为材料的极限应力,对于脆性材料为其强度极限σb,对于塑性材料则为其屈服极限σs;k是安全因数。
③优点结构在设计荷载作用下,大多数仍处于弹性阶段,因此弹性分析对于研究结构的实际工作状态及其性能仍是很重要的。
④缺点按许用应力法以个别截面的局部应力来衡量整个结构的承载能力是不够经济合理的,而且以确定许用应力的安全因数k也不能反映整个结构的强度储备。
(2)塑性分析方法①定义塑性分析方法是指以结构进入塑性阶段并最后丧失承载能力时的极限状态作为结构破坏的标志的结构分析方法。
②极限载荷极限荷载是指结构在极限状态时所能承受的荷载。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
MA = B
3FP l 16
FP FPs C B 5FP l 32
A l /2 MC =
l /2
Mu
FP s FP FPu C B
Mu C A
FP = FPu B Mu
A
All Rights Reserved 重庆大学土木工程学院®
14.4.2 超静定梁极限荷载 Pu的计算方法 超静定梁极限荷载F 1、静力法 、 根据极限状态弯矩图,应用平 根据极限状态弯矩图 应用平 衡条件求解
All Rights Reserved 重庆大学土木工程学院®
【例14-3】试用静力法求图示单跨超静定梁的极限荷载。已 】试用静力法求图示单跨超静定梁的极限荷载。 知该梁的极限弯矩为 Mu 极限状态下
q A Mu l B
ql qx 2 M u M ( x) = x − x − 2 l 2
FPu (6θ ) − 2Muθ − Mu (3θ +θ ) = 0 FPu = 6Mu /6m =1Mu /m = 20kN⋅ m/m = 20kN
All Rights Reserved 重庆大学土木工程学院®
A 2 Mu 4m
B
D Mu 2m 2m
C
A2 A1 A 2Mu B2 B1 B Mu D Mu
A C
C
FP B
W总 = W1 + W2 = 0
l W1 = FPu ∆ = FPu ( θ1 ) 2
l /2
l /2
W2 = − M u (θ1 + 2θ1 ) = − M u (3θ1 ) A
l W总 = W1 + W2 = FPu ( θ1 ) − M u (3θ1 ) = 0 2
Mu
1
FPu Mu Mu B
FPu Mu D C 3 4 2m
C
A
Mu
D= 6
2Mu 6m
1 2= 2 1
FPபைடு நூலகம் = 6 M u / l
All Rights Reserved 重庆大学土木工程学院®
14.4.3 超静定梁极限荷载 Pu的计算特点 超静定梁极限荷载F
1) 无需考虑结构弹塑性变形的发展过程以及塑性铰形成 的顺序,只需预先判定最后的破坏机构。 的顺序,只需预先判定最后的破坏机构。 2) 无需考虑变形协调条件,只需考虑极限状态下机构的平 无需考虑变形协调条件, 衡条件(极限平衡法)即可求得,因而, 衡条件(极限平衡法)即可求得,因而,比弹性计算简 单。 3)不受温度变化、支座移动等因素的影响。这些因素只影 不受温度变化、支座移动等因素的影响。 不受温度变化 响结构变形的发展过程,而不影响极限荷载的数值。 响结构变形的发展过程,而不影响极限荷载的数值。 因为超静定结构在变为机构之前,已先成为静定结构。 因为超静定结构在变为机构之前,已先成为静定结构。 4)不能使用叠加原理,因而每种荷载组合都需要单独进 )不能使用叠加原理, 行计算。 行计算。
B M (x) FBy = ql /2 - Mu /l
Mu
极限荷载
All Rights Reserved
Mu M qu = = 11.66 2u 2 l (1.5 − 2) l
重庆大学土木工程学院®
1
所示变截面梁的极限荷载。 【例14-4】试求图 】试求图14-8a所示变截面梁的极限荷载。已知 所示变截面梁的极限荷载 已知AB 2M 段的极限弯矩为 段的极限弯矩为 u = 40kN ⋅ m ,BC段的极限弯矩为 Mu = 20kN⋅ m
FPu l / 4 = (0.5 + 1) M u
A C
C
FP B
l /2
l /2
极限荷载
Mu C A
FP = FPu B Mu
FPu = 6 M u / l
All Rights Reserved
重庆大学土木工程学院®
2、机构法(虚功法、机动法) 、机构法(虚功法、机动法) 取梁的破坏机构,如图所示。 取梁的破坏机构,如图所示。 给体系一个虚位移
ql Mu − qx − =0 2 l ql qx 2 M u x = Mu x− − 2 l 2 (a) (b)
Mu
确定跨中塑性铰位置
dM ( x) dx = 0, 令 M ( x) = M u ,
x0 x C A
跨中塑性铰位置为
x0 = ( 2 − 1)l = 0.414l
14.4 单跨超静定梁的极限荷载
14.4.1 超静定梁的破坏过程 静定梁,只要有一个截面出现塑性铰,梁就成为机构。 静定梁,只要有一个截面出现塑性铰,梁就成为机构。 在超静定梁中,由于具有多余约束,因此, 在超静定梁中,由于具有多余约束,因此,必须有足够 多的塑性铰出现, 多的塑性铰出现,梁才形成机构 。
FP
形成极限状态需有两个塑性铰, 形成极限状态需有两个塑性铰,而 可能出现塑性铰的截面有三个, 可能出现塑性铰的截面有三个,即 除了A、 截面外还有截面突变处 截面外还有截面突变处B 除了 、D截面外还有截面突变处 1) B、D不可能同时出现塑性铰 、 不可能同时出现塑性铰 2) A、D可能同时出现塑性铰 、 可能同时出现塑性铰 可按破坏机构列写虚功方程
