高中数学必修五课件 余弦定理
合集下载
高中数学必修五北师大版 余弦定理课件(30张)

a c 方法一 由正弦定理sin A=sin C得: 3 5× 2 csin A 5 3 sin C= a = 7 = 14 . 5 3 ∴最大角 A 为 120° ,sin C= . 14 a2+b2-c2 72+32-52 11 解法二 ∵cos C= = = , 2ab 2×7×3 14 ∴C 为锐角,∴sin C= 1-cos C=
[ 分析 ] 可先由大边对大角,确定出最大的角,再由正、余弦定 理求出最大角及sin C.
[解析] ∵a>c>b,∴A 为最大角.
由余弦定理变形得: b2+c2-a2 32+52-72 1 cos A= 2bc = =-2. 2×3×5 又∵0° <A<180° ,∴A=120° . 3 ∴sin A=sin 120° =2.
)
2a2 = 2a =a=2.
答案:C
2.在△ABC中,如果sin A∶sin B∶sin C=2∶3∶4,那么cos C等
于________.
解析:由条件可设 a=2t,b=3t,c=4t a2+b2-c2 4t2+9t2-16t2 1 cos C= 2ab = =-4. 2×2×3t2
1 答案:-4
1.2 余弦定理
第1课时 余弦定理
பைடு நூலகம்
1.能证明余弦定理,了解并可以从向量方 法、解析方法和三角方法等多种途径证 明余弦定理; 重点:余弦定理的理 解和简单应用.
2.能够应用余弦定理及其推论解三角形; 难点:余弦定理的推 3.了解余弦定理与勾股定理之间的联系, 导及解决简单的三角 知道解三角形问题的几种情形及其基本 解法. 形度量问题.
1 3 3 解法二 由 b<c,B=30° ,b>csin 30° =3 3×2= 2 知本题有两解. 1 3 3×2 csin B 3 由正弦定理 sin C= = = , b 3 2 ∴C=60° 或 120° , 当 C=60° 时,A=90° , 由勾股定理 a= b2+c2= 32+3 32=6,
必修五 余弦定理PPT课件

c2a2b22 acbo Cs
A
证明:ABACCB
b
c
A•B A B (A C C)• B (A C C)B
A•C A C 2 A•C C B•C BC Ba
B
∴ A B 2 = A C 2 + 2 A C C B c o s ( 1 8 0 0 - C ) + C B 2
∴ c 2=a 2+b 2-2 a b c o s C
5
证明 格式二:逆用公式 ababcos
证明: b2 + c 2 -2 b c ·cos A
2
2
= AC + AB -2· AC ·AB ·cos A
2
2
= AC + AB -2· AC ·AB
C
B
2
=( AC - AB )
A
2
= BC
2
同理可证:
= BC
=a2
b2=a2+ c2- 2· bc· co Bs
A c
b
D
Ca
B
8
证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA
b A
C
a 2 C D 2 B D 2
(b sinA )2 (c b co sA )2
a b 2 s in 2 A c 2 b 2 c o s 2 A 2 b c c o s A
c2=a2+ b2- 2· abcoCs
6
证明
解析法
y
证明:以CB所在的直线为x轴,过C点
垂直于CB的直线为y轴,建立如图所
示的坐标系,则A、B、C三点的坐标
分别为:
高中数学必修5优质课件:余弦定理
第八页,编辑于星期日:二十三点 三十九分。
[对点训练]
2.在△ABC,已知 a=2 2,b=2 3,C=15°,解此三角形.
解:c2=a2+b2-2abcos C=(2 2)2+(2 3)2-2×2 2×2 3 ×cos(45°-30°)=8-4 3=( 6- 2) 2 ∴c= 6- 2. 法一:由余弦定理的推论得
第二十页,编辑于星期日:二十三点 三十九分。
2.在△ABC 中,角 A、B、C 的对边分别为 a、b、c,若c2-2aa2b-b2
>0,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.是锐角或直角三角形
解析:由c2-2aa2b-b2>0 得-cos C>0,
所以 cos C<0,从而 C 为钝角,因此△ABC 一定是钝角
三角形.
答案:C
第二十一页,编辑于星期日:二十三点 三十九 分。
3.在△ABC 中,角 A,B,C 所对边的长分别为 a,b,c. 若 a=2,B=π6,c=2 3,则 b=________. 解 析 : 由 余 弦 定 理 得 b2= a2+ c2 - 2accos B= 4+ 12 - 2×2×2 3× 23=4,所以 b=2. 答案:2
第十四页,编辑于星期日:二十三点 三十九分。
[对点训练] 3.已知:在△ABC 中,cos A=35,a=4,b=3,则 c=________. 解析:A 为 b,c 的夹角,由余弦定理得 a2=b2+c2-2bccos A, ∴16=9+c2-6×35c, 整理得 5c2-18c-35=0. 解得 c=5 或 c=-75(舍). 答案:5
[对点训练] 4.在△ABC 中,若 cos A=ssiinn BC,试判断其形状. 解:由cos A=ssiinn BC得cos A=bc,即b2+2cb2c-a2=bc, ∴b2+c2-a2=2b2,即a2+b2=c2, 因此△ABC是以C为直角的直角三角形.
[对点训练]
2.在△ABC,已知 a=2 2,b=2 3,C=15°,解此三角形.
解:c2=a2+b2-2abcos C=(2 2)2+(2 3)2-2×2 2×2 3 ×cos(45°-30°)=8-4 3=( 6- 2) 2 ∴c= 6- 2. 法一:由余弦定理的推论得
第二十页,编辑于星期日:二十三点 三十九分。
2.在△ABC 中,角 A、B、C 的对边分别为 a、b、c,若c2-2aa2b-b2
>0,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.是锐角或直角三角形
解析:由c2-2aa2b-b2>0 得-cos C>0,
所以 cos C<0,从而 C 为钝角,因此△ABC 一定是钝角
三角形.
答案:C
第二十一页,编辑于星期日:二十三点 三十九 分。
3.在△ABC 中,角 A,B,C 所对边的长分别为 a,b,c. 若 a=2,B=π6,c=2 3,则 b=________. 解 析 : 由 余 弦 定 理 得 b2= a2+ c2 - 2accos B= 4+ 12 - 2×2×2 3× 23=4,所以 b=2. 答案:2
第十四页,编辑于星期日:二十三点 三十九分。
[对点训练] 3.已知:在△ABC 中,cos A=35,a=4,b=3,则 c=________. 解析:A 为 b,c 的夹角,由余弦定理得 a2=b2+c2-2bccos A, ∴16=9+c2-6×35c, 整理得 5c2-18c-35=0. 解得 c=5 或 c=-75(舍). 答案:5
[对点训练] 4.在△ABC 中,若 cos A=ssiinn BC,试判断其形状. 解:由cos A=ssiinn BC得cos A=bc,即b2+2cb2c-a2=bc, ∴b2+c2-a2=2b2,即a2+b2=c2, 因此△ABC是以C为直角的直角三角形.
数学:1.1.2《余弦定理》课件(新人教b版必修5)

1 2
AB
1
3 2
3 AB 4. C
AC 2 AB 2 BC 2 2 AB BC COSB
16 1 2 41 1 13 AC 13.
A
2
Ac 2 BC 2 AB 2 13 1 16
13
cosC
B
2 AC BC
2 13 1 13
sinC
1
13 13
2
2 26 13
1.1.2 余弦定理 课件
2024/11/11
1.正弦定理:在任一个三角形中,各边和它所对角的正弦比相等,
即a =
sin A
b sin B
=
c =2R(R为△ABC外接圆半径)
sin C
2.正弦定理的应用: 从理论上正弦定理可解决两类问题: 1.两角和任意一边,求其它两边和一角;
2.两边和其中一边对角,求另一边的对角,进而可求其它的边和 角。
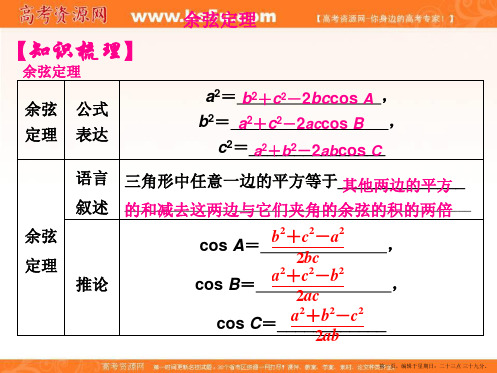
c2 a2 b2 2ab cosC
2024/11/11
1.余弦定理 :三角形任何一边的平方等于其他两边平方的和减去 这两边与它们夹角的余弦的积的两倍。
b2 c2 a2
即 a2 b2 c2 2bc cos A cos A 2bc
b2 c2 a2 2ac cosB cos B c2 a2 b2
2ab
2024/11/11
2.在△ABC中,若a2>b2+c2,则△ABC为 钝角三角形;若a2=b2+c2,
则△ABC为
直角三;角若形a2<b2+c2且b2<a2+c2且c2<a2+b2,
则△ABC为
锐角。三角形
3.在△ABC中,sinA=2cosBsinC,则三角形为 等腰三角形 。
高中数学第二章解三角形2.1.2余弦定理课件北师大版必修5

1
2
3
4
5
1.在△ABC 中,已知 a=5,b=4,C=120°,则 c 的长为(
A. 41
C. 41或 61
)
B. 61
D. 21
1
解析: 因为 c2=a2+b2-2abcos C,所以 c2=52+42-2×5×4× - 2 =61,即
c= 61.
答案:B
1
2
3
4
5
2.在△ABC中,若bcos A=acos B,则△ABC是(
角A,B,C的对边,且b2,c2是关于x的一元二次方程x2-(a2+bc)x+m=0的
两根.
(1)求角A的大小;
(2)若 a= 3 ,设B=θ,△ABC的周长为y,求y=f(θ)的最大值.
分析:(1)利用余弦定理求出角A;(2)先利用正弦定理将△ABC的周
长y表示成关于θ的函数,再结合三角函数的性质进行求解.
探究一
探究二
探究三
思维辨析
解:(1)在△ABC中,依题意有b2+c2=a2+bc,即b2+c2-a2=bc,
所以 cos
2
+2 -2
A=
2
1
2
= ,
π
3
又因为 A∈(0,π),所以 A= .
π
3
(2)由 a= 3,A= ,及正弦定理得
sin
=
所以 b=2sin B=2sin θ,c=2sin C=2sin
1 .2
余弦定理
学 习 目 标
1.掌握余弦定理及其证明.
2.会用余弦定理解决两类解三角形问题.
3.能综合应用正弦定理与余弦定理解决三角形
《余弦定理》公开课教学PPT课件【高中数学必修5(北师大版)】

cos A b2 c2 a2 2bc
87.82 161.72 134.6 287.8161.7
2
0.5543,
cos
B
c2
a2 b2 2ca
134.62 161.72 87.8 2134.6161.7
2
0.8398,
C 1800 (A B)1800 (5602032053) 90047. [来源
;
A56020 ; B32053 ;
B
a2
c2 b2 2ac
cosC
b2
a2 2ba
c2
新课学习
[理解定理] 从而知余弦定理及其推论的基本作用为: ①已知三角形的任意两边及它们的夹角就可以求出第三边 ; ②已知三角形的三条边就可以求出其它角。
新课学习
思考:勾股定理指出了直角三角形中三边平方之
间的关系,余弦定理则指出了一般三角形中三边平方 之间的关系,如何看这两个定理之间的关系?
又∵
6
2 > 2.41.43.8,
2 3 < 21.83.6, ∴ a < c , 即 00 < A < 900, ∴ A600.
评述:解法二应注意确定A的取值范围。
新课学习
例2:在△ABC中,已知a=134.6cm,b=87.8cm,c=161.7cm,解三角形
新课学习
解:由余弦定理的推论得:
[来源:学+
新课总结
(1)余弦定理是任何三角形边角之间存在的共同规律, 勾股定理是余弦定理的特例; (2)余弦定理的应用范围: ①.已知三边求三角; ②.已知两边及它们的夹角,求第三边。
再见
北师大版·统编教材高中数学必修5
第二章 · 第一节
正弦定理与余弦定理
高中数学必修五 2.1余弦定理-课件

A≈44°
cosC=
a2+b2-c2 2ab =0.8071,
C≈36°
∴ B=180°-(A+C)≈100°.
第十二页,编辑于星期日:二十三点 五十二分。
2. ΔABC中,a=2,b=2 ,2 C=15°,解此三角形.
解:∵ c 2 a 2 b2 2ab cos C=8-4 3
∴c= 6 2
1.2余弦定理
第一页,编辑于星期日:二十三点 五十二分。
问题提出
在三角形中,已知两边及其夹角,怎么求出此角的对边? 已知三条边,怎么求出它的三个角呢?
第二页,编辑于星期日:二十三点 五十二分。
分析理解
如图,根据向量的数量积,可以得到
a2 BC • BC
(AC AB) • (AC AB)
AC2 2AC • AB AB2 A
解.在△BCD中,BC=1,CD=1,∠BCD=135O.
因为 BD2 BC2 CD2 2BC • CD cos BCD 12 12 211cos135 2 2
所以 BD 1.8 在△ABD中,AB=1, BD 2 2 , AD 3 因为 cos DAB AB2 AD2 BD2
2AB • AD
第十页,编辑于星期日:二十三点 五十二分。
12 ( 3)2 (2 2) 21 3
0.1691 所以 DAB 80
第十一页,编辑于星期日:二十三点 五十二分。
1. 在ABC中,已知a=7,b=10, c=6,求A、B和C.
解:∵
∴
∵
∴
cosA=
b2+c2-a2 2bc
=0.725,
例4:如图,有两条直线AB和CD相交成80O角,交点是O.甲乙两 人同时从点O分别沿OA,OC方向出发,速度分别为4km/h和 4.5km/h.3时后两人相距多远(结果精确到0.1km)?
人教版高中数学必修5(A版) 1.1.2《余弦定理》 PPT课件

A
c a
B
C
余弦定理:
三角形中任何一边的平方等于其他 两边的平方的和减去这两边与它们的夹 角的余弦的积的两倍.
余弦定理:
三角形中任何一边的平方等于其他 两边的平方的和减去这两边与它们的夹 角的余弦的积的两倍. 即:
a b c 2bc cos A 2 2 2 b a c 2ac cos B 2 2 2 c a b 2ab cos C
复习引入
运用正弦定理能解怎样的三角形?
A
C
B
复习引入
运用正弦定理能解怎样的三角形? ①已知三角形的任意两角及其一边; ②已知三角形的任意两边与其中一边 的对角.
A C B
情境设置
问题1:
如果已知三角形的两边及其夹角, 根据三角形全等的判定方法,这个三 角形是大小、形状完全确定的三角形. 从量化的角度来看,如何从已知的两 边和它们的夹角求三角形的另一边和 两个角?
练习:
教材P. 8练习第1题. 在△ABC中,已知下列条件,解三角
形(角度精确到1 , 边长精确到0.1cm):
(1) a=2.7cm,b=3.6cm,C=82.2 ; (2) b=12.9cm,c=15.4cm,A=42.3 .
o o
o
课堂小结
1. 余弦定理是任何三角形边角之间存在 的共同规律,勾股定理是余弦定理的特 例; 2. 余弦定理的应用范围: ①已知三边求三角; ②已知两边及它们的夹角,求第三边.
思考4:
勾股定理指出了直角三角形中三边 平方之间的关系,余弦定理则指出了一 般三角形中三边平方之间的关系,如何 看这两个定理之间的关系?
思考4:
勾股定理指出了直角三角形中三边 平方之间的关系,余弦定理则指出了一 般三角形中三边平方之间的关系,如何 看这两个定理之间的关系?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:∵a:b:c=2: 6:( 3+1), 令a=2k,b= 6k,c=( 3+1)k(k>0). 由余弦定理的推论得 b2+c2-a2 6+ 3+12-4 2 cosA= = = ,∴A=45° . 2bc 2× 6× 3+1 2 a2+c2-b2 4+ 3+12-6 1 cosB= 2ac = =2,∴B=60° . 2×2× 3+1 ∴C=180° -A-B=180° -45° -60° =75° .
[分析] 将四边形 ABCD 分成△ABD 和△BCD,在△ABD 中,用余 弦定理求出 BD,在△BCD 中,用正弦定理即可解出 BC.
[解] △ABD 中, 由余弦定理得 AB2=AD2+BD2-2AD· BD· cos∠ADB, 设 BD=x, 则有 142=102+x2-2×10xcos60° , 即 x2-10x-96=0, 解得 x1=16,x2=-6(舍去), ∴BD=16. ∵AD⊥CD,∠BDA=60° , ∴∠CDB=30° . 16 在△BCD 中,由正弦定理得 BC=sin135° · sin30° =8 2.
[点评]
1.解三角形时,应先分析题设条件,如本题属
于“SAS”型,先用余弦定理求a,在此基础上,可以利用余 弦定理计算角B或C的余弦值,也可以利用正弦定理计算角 B或C的正弦值. 2.常用余弦定理解答两类题目“SAS”型及“SSS”型.
变式训练 1 已知在△ABC 中,a:b:c=2: 6:( 3+1),求△ABC 的 各角度数.
1.1.2 余弦定理
1.余弦定理 三角形中任何一边的平方 等于其他两边的平方的和减去 这两边与它们的夹角的余弦的 积的两倍.即
若 a,b,c 分别是△ABC 的顶 点 A,B,C 所对的边长,则
b +c -2bccosA a =__________________ ,
2 2
2 2
a +c -2accosB b =__________________ ,
各角 ; (1)已知三边,求_____
第三边和其他两个角 (2)已知两边和它们的夹角,求 __________________.
思考感悟
1 .已知三角形任意两边与一 角,借助于正、余弦定理是否能求 出其他元素?
2. 在解三角形的过程中, 求某一个角有时既可以用余 弦定理,也可以用正弦定理,两种方案有什么利弊呢?
典例导悟
类型一 利用余弦定理解三角形 [例 1]△ABC 中,已知 b=3,c=2 3,A=30° ,求边 a、 角 C 和角 B.
[解] 直接应用余弦定理:
a2=b2+c2-2bccosA =32+(2 3)2-2×3×2 3×cos30° =3,∴a= 3. a2+c2-b2 32+2 32-32 1 ∴cosB= = =2. 2ac 2× 3×2 3 ∴B=60° ,∴C=180° -A-B=180° -30° -60° =90° .
须知余弦定理是勾股定理的推广,勾股定理是余弦定
2 2 2 a > b + c 理的特例.角A为钝角⇔_____________,角A为直角⇔ 2 2 2 2 2 2 a = b + c a < b + c ____________,角A为锐角⇔____________.
3.利用余弦定理可解决的两类问题 余弦定理的每一个等式中都包含四个不同的量, 它们分 别是三角形的三边和一个角, 知道其中的三个量, 代入等式, 便可求出第四个量来. 利用余弦定理可以解决以下两类解斜三角形的问题:
∴a2=b2+c2-bc. 又∵a2=b2+c2-2bccosA,则2cosA=1,∴A=60° . 又∵sinA=sin(B+C)=sinBcosC+cosBsinC= 2sinBcosC,∴sin(B-C)=0,∴B=C. 又∵B+C=120° ,∴△ABC是等边三角形.
[点评]
判断三角形形状的方法
2A
1+cosA b+c b 2 = 2c ,∴cosA=c . b2+c2-a2 b 根据余弦定理得 = , 2bc c ∴b2+c2-a2=2b2,即a2+b2=c2. ∴△ABC是直角三角形.
类型三 正、余弦定理的综合应用 [例 3] 如图所示,在四边形 ABCD 中,AD⊥CD,AD =10,AB=14,∠BDA=60° ,∠BCD=135° ,求 BC 的长.
类型二 [例2]
判断三角形的形状 在△ABC中,已知(a+b+c)(b+c-a)=3bc且
sinA=2sinBcosC,试确定△ABC的形状. [分析] 首先根据条件(a+b+c)(b+c-a)=3bc,利
用余弦定理求出一个角,再利用另一个条件,得到另外两 个角的关系,即可判断.
[解]
∵(a+b+c)(b+c-a)=3bc,
a +b -2abcosC c =__________________.
2
2 2
2
2
2.余弦定理的推论 余弦定理揭示了三角形中两边及其夹角与 对边之间的关系,它的另一种表达形式是 2 2 2 b +c -a cosA=_____________ , 2bc 2 2 2 a +c -b cosB=_____________ , 2ac 2 2 2 a +b -c cosC=_____________. 2ab
提示:用余弦定理求角时,运算量较大,但角与余弦 值是一一对应的,无须讨论;而用正弦定理求角时,运算 量较小,但由于在区间(0,π)上角与正弦值不是一一对应 的,一般情况下一个正弦值可对应两个角,往往要依据角 的范围讨论解的情况.
3.怎样用余弦定理判断三角形的形状?
提示:(1)在△ABC中,若a2<b2+c2,则0° <A<90° ;反 之,若0° <A<90° ,则a2<b2+c2. (2)在△ABC中,若a2=b2+c2,则A=90° ;反之,若A =90° ,则a2=b2+c2. (3)在△ABC中,若a2>b2+c2,则90° <A<180° ;反之, 若90° <A<180° ,则a2>b2+c2.
(1)利用正、余弦定理化角成边,利用代数运算求出三 边的关系; (2)由正、余弦定理化边为角,通过恒等变形及内角和 定理得到内角关系,从而判定形状.
b+c 变式训练2 在△ABC中,已知cos 2 = 2c (a,b,c分
2A
别为角A,B,C的对边),判断△ABC的形状.
b+c 解:在△ABC中,由已知cos 2 = 2c 得
