九年级数学实际问题与二次函
九年级数学实际问题与二次函数教学反思

九年级数学实际问题与二次函数教学反思(一)二次是函数是函数中的重点、难点,它比较复杂,一般来说我们研究它是先研究其本身性质、图象,进而扩展到应用,它在现实中应用较广,我们在教学中要紧密结合实际,让学生学有所用,在教学中应注意以下几个问题:(一)把握好课标。
九年义务教育初中数学教学大纲却降低了对二次函数的教学要求,只要求学生理解二次函数和抛物线的有关概念,会用描点法画出二次函数的图像;会用配方法确定抛物线的顶点和对称轴;会用待定系数法由已知图像上三点的坐标求二次函数的解析式。
(二)把实际问题数学化。
首先要深入了解实际问题的背景,了解影响问题变化的主要因素,然后在舍弃问题中的非本质因素的基础上,应用有关知识把实际问题抽象成为数学问题,并进而解决它。
(三)函数的教学应注意自变量与函数之间的变化对应。
函数问题是一个研究动态变化的问题,让学生理解动态变化中自变量与函数之间的变化对应,可能更有助于学生对函数的学习。
(四)二次函数的教学应注意数形结合。
要把函数关系式与其图像结合起来学习,让学生感受到数和形结合分析解决问题的优势。
(五)建立二次函数模型。
利用二次函数来解决实际问题,重在建立二次函数模型。
但是在解决最值问题时得注意,有时理论上的最大值(或最小值)不是实际生活中的最值,得考虑实际意义。
(六)注重二次函数与一元二次方程、一元二次不等式的关系。
利用二次函数的图像可以得到对应一元二次方程的解、一元二次不等式的解集。
九年级数学实际问题与二次函数教学反思(二)这节课我是采用先让学生按照学案的提示,自主预习课本,受到课本所给出的分析过程的思维限制,很容易把问题解决了,但没有放手让学生从不同角度去尝试建立坐标系,体会各种情况下所建立的坐标系是否有利于点的表示,没有激发学生学习的热情,没有给予学生以启迪。
用二次函数知识解决实际问题是本章学习的一大难点,遇到实际问题学生往往无从下手,学生在解题过程中遇到一个新的问题该如何去联想?联想什么?怎样联想?这与课堂教学过程中老师解题方法的讲授至关重要,老师在课堂教学过程中应如何引导学生判断、分析、归类。
22-3 实际问题与二次函数(3)

1 2 这条抛物线表示的二次函数为 y x 教材导读 2
2
解得 x1 6 , x2 6 水面的宽度 2 x 2 6 m
水面下降1cm,水面宽度增加____________m. 2 6 4
1 2 解: 3 x 2
x 6
2
1
-2
-1
1 -1 -2
2
-3
解法二
22-3 实际问题与二次函数(3)
人教版九年级数学上册
第
3 课时
利润问题
课件说明
• 二次函数是单变量最优化问题的数学模型,如生活中 涉及的求最大利润,最大面积等。这体现了数学的实 用性,是理论与实践结合的集中体现。本节课主要研 究建立坐标系解决实际问题.
阅读教材第51页至52页,明确学习目标
学习目标:
4 所以该车不能通过隧道
2、一场篮球赛中,球员甲跳起投篮,如图2,已知球在 A处出手时离地面20/9 m,与篮筐中心C的水平距离是 7m,当球运行的水平距离是4 m时,达到最大高度4m (B处),设篮球运行的路线为抛物线。篮筐距地面 3m。 ①问此球能否投中?
测评反馈
(选做)②、此时对 方球员乙前来盖帽。 已知乙跳起后摸到的 最大高度为3.19m, 他如何做才能盖帽成 功?
问题1: 图中是抛物线形拱桥,当拱顶离水面 2 m时,水面 宽 4 m 。水面下降 1 m,水面宽度增加多少? (1)求宽度增加多少需要什 么数据?
教材导读 (2)表示水面宽的线段的端 点在哪条曲线上?
探究“拱桥”问题
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
解决抛物线型建筑问题“三步骤” 1、根据题意,建立恰当的坐标系,合理地设出所求的 函数的表达式。 2、准确转化线段的长与点的坐标之间的关系,得到抛 物线上点的坐标,代入解析式,求出二次函数解析式。 3、应用所求解析式及其性质解决问题。
实际问题与二次函数知识点总结和重难点精析

实际问题与二次函数知识点总结和重难点精析一、实际问题与二次函数的定义和基本性质在九年级数学中,我们学习了二次函数的基本概念、表示方法和性质。
二次函数是指形如y = ax²+bx+c(a≠0)的函数,其中a、b、c为实数。
二次函数的图像是一个抛物线,具有以下基本性质:1.二次项系数a决定抛物线的开口方向和大小。
2.一次项系数b和二次项系数a共同决定抛物线的对称轴位置。
3.常数项c决定抛物线与y轴的交点。
二、实际问题与二次函数的解题方法解决实际问题时,需要灵活运用二次函数的性质和解题方法。
下面列举几种常见的解题方法:1.图像法:通过观察二次函数的图像,直接得出答案。
例如,在解决几何问题时,可以通过画图直接找出答案。
2.公式法:根据二次函数的公式,直接代入已知数进行计算。
例如,在解决代数问题时,可以运用二次方程求根公式等。
3.配方法:将二次函数化为顶点式,然后根据抛物线的性质进行解题。
例如,在解决最大值或最小值问题时,可以采用配方法。
4.因式分解法:将二次函数化为两个一次因式的乘积,然后通过解方程组得出答案。
例如,在解决某些代数问题时,可以采用因式分解法。
三、重难点精析1.重难点知识点介绍(1)二次函数的图像和性质:如何根据图像判断抛物线的开口方向、对称轴、顶点坐标等;如何根据性质求出抛物线的最值、单调区间等。
(2)二次函数的应用题:如何根据实际问题建立二次函数模型;如何求解模型得出实际问题的答案;如何验证答案的正确性。
2.解题思路和技巧(1)对于图像题,可以采用数形结合的方法,将抽象的数学问题转化为形象的图像问题,从而简化解题过程。
(2)对于性质题,需要熟练掌握抛物线的各种性质,例如最值、单调性等,从而可以灵活运用到解题中。
(3)对于应用题,需要认真审题,将实际问题转化为数学问题,然后建立模型求解。
同时需要注意答案的合理性和实际意义的符合性。
3.解题错误分析(1)对于图像题,可能出现的错误是将图像中的信息误解或遗漏,导致答案错误。
22.3实际问题与二次函数 课件人教版数学九年级上册

【综合拓展类作业】
(2)设利润为w 当22≤x≤30 时 ,w=(x-20)(-x+70)=-x²+90x-1400=-(x45)²+625 ∵在22≤x≤30 范 围 内 ,w 随着x的增大而增大, ∴当x=30 时 ,w 取得最大值为400;
当30<x≤45 时 ,w=(x-20)(-2x+100)=-2x²+140x-2000=2(x-35)²+450 ∴当x=35 时 ,w 取得最大值为450 ∵450>400,
篱笆总长为900 m (篱笆的厚度忽略不计),当AB=_ 150 _m 时,矩形土
地ABCD 的面积最大.
B
F
C
【知识技能类作业】选做题:
3. 北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不 同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近 似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A, B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90 米), 以最高点O 为坐标原点,以平行于AB 的直线为x轴建立平面直角坐标系,则此抛物 线钢拱的函数表达式为( B )
(1)求S与x的函数关系式及自变量的取值范围; (2)当x取何值时所围成的花圃面积最大,最大值是多少? (3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
解:1)S=x(24 -4x)=-4x²+24x(0<x<6)
2)当
时,
3)∵墙的可用长度为8米 ∴0<24 -4x ≤8 ∴4≤x<6 ∴当x=4cm时,S最大值=32平方米
有关抛物线形的实际问题的一般解题思路。 (1)建立适当的平面直角坐标系。 (2)根据题意找出已知点的坐标。 (3)求出抛物线解析式。 (4)直接利用图象解决实际问题。
2023年九年级数学中考专题:实际问题与二次函数压轴应用题

2023年九年级数学中考专题:实际问题与二次函数压轴应用题1.某工厂生产A 型产品,每件成本为20元,当A 型产品的销售单价为x 元时,销售量为y 万件.要求每件A 型产品的销售单价不低于20元且不高于28元.经市场调查发现,y 与x 之间满足一次函数关系,且当x =23时,y =34;x =25时,y =30.(1)求y 与x 的函数关系式,并写出自变量x 的取值范围;(2)若某次销售刚好获得182万元的利润,则每件A 型产品的销售单价是多少元?(3)设该工厂销售A 型产品所获得的利润为w 万元,将该产品的销售单价定为多少元时,才能使销售该产品所获得的利润最大?最大利润是多少万元?2.如图,有长为24m 的篱笆,一面利用墙(墙的最大可用长度a 为12m )围成中间隔有一道篱笆的矩形花圃,设花圃的宽AB 为m x ,面积为2m S .(1)求S 与x 的函数表达式.(2)如果要围成面积为245m 的花圃,AB 的长是多少米?(3)根据(1)中求得的函数关系式,判断当x 取何值时,花圃的面积最大?最大面积是多少?3.2022年2月4日,第24届冬季奥林匹克运动会在北京举行,吉祥物“冰墩墩”备受人民的喜爱,某商店经销吉祥物“冰墩墩”玩具,销售成本为每件40元,据市场分析,若按每件50元销售,一个月能售出500件;销售单价每涨1元,月销售量就减少10件,针对这种玩具的销售情况,请解答以下问题:(1)求当销售单价涨多少元时,月销售利润能够达到8000元;(2)商店想在月销售成本不超过9000元的情况下,使得月销售利润达到8000元,求销售定价应为多少元?4.某大型商场准备购买一批A 型和B 型商品,已知一件A 型商品的进价比一件B 型商品的进价多30元,用6000元采购A 型商品的件数是用1200元采购B 型商品的件数的2倍.(1)求一件A ,B 型商品的进价分别为多少元?(2)该商场购进A 型和B 型商品若干,准备采取“买二送一”的优惠销售方案,即:买两件A 型商品赠送一件B型商品,通过一段试销发现A 型商品每天的销售量y (件)与A 型商品的销售单价x (元)满足:2200y x =-+,若商场继续以上述优惠销售方案进行销售,当A 型商品的销售单价定为多少元时,每天的销售利润最大,并求出此时的最大销售利润.5.某数学兴趣小组想借助如图所示的直角墙角ADC ∠(两边足够长),用20m 长的篱笆围成一个矩形花园ABCD (篱笆只围AB ,BC 两边).(1)若围成的花园面积为291m ,求矩形花园AB 的长;(2)在点P 处有一棵树与墙CD ,AD 的距离分别为12m 和6m ,要能将这棵树围在花园内(含边界,不考虑树的粗细),又使得花园面积有最大值,求此时矩形花园AB 的长.6.第一届全国青年运动会射箭项目决赛于10月20-24日在福建省莆田市体育公园举行.我市某工艺厂为青运会设计了一款成本为每件20元的工艺品,投放市场进行试销后发现每天的销售量y (件)是售价x (元/件)的一次函数:当售价为20元/件时,每天销售量为800件;当售价为25元/件时,每天的销售量为750件.(1)求y 与x 的函数关系式(2)如果该工艺品售价最高不能超过每件50元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)7.中秋节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:小王:该水果的进价是每千克22元;小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低1元,每天的销售量将增加40千克.根据他们的对话,解决下面所给问题:设降价(0)x x >元,每天所获得的利润为w 元.(1)超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?(2)这种水果的销售价定为多少时,可使每天销售利润最大?最大的利润是多少?8.贫困户李大爷在某单位精准扶贫工作队的帮扶下,将一片坡地改造后种植了优质水果蓝莓,经核算,种植成本为18元/千克.今年正式上市销售,通过30天的试销发现:①第1天卖出20千克,以后每天比前一天多卖4千克:②销售价格y (元/千克)与时间x (天)之间满足如下函数关系:76(120)(2030)mx m x x y n x x -≤<⎧=⎨≤≤⎩,为正整数,为正整数,且第12天的售价为32元/千克,第23天的售价为25元/千克. (1)填空:m =_______,n =_______;试销中销售量P (千克)与时间x (天)之间的函数关系式为_______;(2)求销售蓝莓第几天时,当天的利润W 最大?最大利润是多少元?(3)求试销的30天中,当天利润W 不低于870元的天数共有几天?9.某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月售出500kg ,销售价每涨价1元,月销售量就减少5kg .(1)当销售单价定为60元时,计算月销售量和销售利润.(2)商店想让顾客获得更多实惠的情况下,使月销售利润达到9000元,销售单价应定为多少?(3)当售价定为多少元时会获得最大利润?求出最大利润.10.某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)](1)根据以上信息,求y关于x的函数关系式.(2)①填空:该产品的成本单价是元,表中a的值是.②求该商品日销售利润的最大值.ABCD,墙长为25米.设11.小茗同学准备用一段长为50米的篱笆在家修建一个一边靠墙的矩形花圃(矩形)花圃的一边AD为x米.(1)如图1,写出花圃的面积S(平方米)与x(米)的函数关系式;(2)图1中花圃的面积能为300平方米吗?若能,请求出x的值;若不能,请说明理由;(3)为方便进出,小茗同学决定在BC边上留一处长为a米(04)<<的门(如图2),且最终围成的花圃的最大a面积为325平方米,直接写出a的值.12.包河区发展农业经济产业,在大圩乡种植多品种的葡萄,已知某葡萄种植户李大爷的葡萄成本为10元/kg,如果在未来40天葡萄的销售单价p(元/kg)与时间t(天)之间的函数关系式为:120(120)4135(2140)2t t t p t t t ⎧+≤<⎪⎪=⎨⎪+<≤⎪⎩,为整数,为整数,且葡萄的日销量y (千克)与时间t (天)的关系如下表:(1)请直接写出y 与t 之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?(2)在后20天(即2140t ≤≤,t 为整数),请求出哪一天的日销售利润最大?日销售利润最大为多少?(3)在实际销售的前20天中,李大爷决定每销售1千克水果就捐赠n 元利润(8n <)给留守儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间t 的增大而增大,请求出n 的取值范围.13.红灯笼,象征着国家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.(1)求甲、乙两种灯笼每对的进价;(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,若规定每对乙灯笼的利润不能高于30元,设乙灯笼每对售价为x 元,小明一天通过乙灯笼获得利润y 元. ①求出y 与x 之间的函数解析式;②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?14.跳台滑雪是冬季奥运会的比赛项目之一,如图,运动员通过助滑道后在点A 处起跳经空中飞行后落在着陆坡BC 上的点P 处,他在空中飞行的路线可以看作抛物线的一部分,这里OA 表示起跳点A 到地面OB 的距离,OC 表示着陆坡BC 的高度,OB 表示着陆坡底端B 到点O 的水平距离,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y (单位:m )与水平距离x (单位:m )近似满足函数关系:2116y x bx c =-++,已知70m OA =,60m OC =,落点P 的水平距离是40m ,竖直高度是30m .(1)点A 的坐标是_____,点P 的坐标是_______;(2)求满足的函数关系2116y x bx c =-++; (3)运动员在空中飞行过程中,当他与着陆坡BC 竖直方向上的距离达到最大时,直接写出此时的水平距离.15.某商家销售一种纪念品.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y 个,销售单价为x 元.(1)在横线上直接写出y 与x 之间的函数关系式;(2)求当每个纪念品的销售单价是多少元时,商家每天获利2400元;(3)将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w 元最大?最大利润是多少元?16.金秋十月,我省某农业合作社有机水稻再获丰收,加工成有机大米后通过实体和电商两种渠道进行销售.该有机大米成本为每千克 14 元,销售价格不低于成本,且不超过 25 元/千克,根据各销售渠道的反馈,发现该有机大米一天的销售量y (千克)是该天的售价x (元/千克)的一次函数,部分情况如表:(1)求一天的销售量y (千克)与售价x (元/千克)之间的函数关系式并写出x 的取值范围.(2)若某天销售这种大米获利 2400 元,那么这天该大米的售价为多少?(3)该有机大米售价定为多少时,当天获利w 最大?最大利润为多少?17.某公司为了宣传一种新产品,在某地先后举行18场产品促销会,已知该产品每台成本为4万元,设第x 场产品的销售量为y (台),在销售过程中获得以下信息:信息1:已知第一场销售产品38台,然后每增加一场,产品就少卖出2台;信息2:产品的每场销售单价p (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场—第10场浮动价与销售场次x 成正比,第11场—第18场浮动价与销售场次x 成反比,经过统计,得到如下数据:(1)求y 与x 之间的函数关系式;(2)求销售单价p 与销售场次x 之间的函数关系式;(3)当产品销售单价为6.5万元时,求销售场次是第几场?(4)在这18场产品促销会中,哪一场获得的利润最大,最大利润是多少?(结果保留整数)18.某商场经营A 种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x 元()40x >,请用含x 的代数式表示该玩具的销售量______.(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润.(3)该商场计划将(2)中所得的利润的一部分采购一批B 种玩具并转手出售,根据调查准备两种方案: 方案①:月初出售,获利15%,并可用本和利再投资C 种玩具,到月末又可获利10%;方案②:只到月末出售直接获利30%,但要另支付仓库保管费350元.请问商场如何使用这笔资金,采用哪种方案获利较多?尝试填写以下表格.参考答案:1.(1)y 与x 的函数关系式为280y x =-+,自变量x 的取值范围是2028x ≤≤(2)每件A 型产品的销售单价是27元(3)该产品的销售单价定为28元时,才能使销售该产品所获得的利润最大,最大利润是192万元2.(1)()232448S x x x =-+≤<;(2)AB 的长为5m ;(3)当4x =时,围成的花圃的面积最大,最大面积为248m .3.(1)涨10元或30元(2)80元4.(1)一件A ,B 型商品的进价分别为50元,20元(2)A 型商品的销售单价定为80元时,每天的销售利润最大,最大销售利润为800元5.(1)13m 和7m .(2)8m6.(1)101000y x =-+(2)当售价定为50元时,该工艺品每天获得的利润最大,最大利润为12000元.7.(1)每千克29元(2)定为32元时可使每天销售利润最大,最大的利润是4000元8.(1)12-,25,416P x =+; (2)第18天的利润最大,最大利润为968元;(3)共有12天9.(1)销售单价定为60元时,月销售量为450千克,销售利润为9000元(2)销售单价应定为60元(3)当售价定为95元时会获得最大利润,求出最大利润为15125元.10.(1)10900y x =-+(2)①40,4560 ②该商品日销售利润的最大值为6250元11.(1)21252S x x =-+(2)能为300平方米,此时x 的值为20(3)a 的值为112.(1)2120y t =-+;90kg(2)21天,1131元(3)58n ≤<13.(1)甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;(2)①222686930y x x =-+-,②乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.14.(1)()0,70A ,()40,30P ; (2)21370162y x x =-++; (3)18m15.(1)()107404452y x x =-+≤≤(2)当每个纪念品的销售单价是50元时,商家每天获利2400元(3)将纪念品的销售单价定为52元时,商家每天销售纪念品获得的利润w 元最大,最大利润是2640元16.(1)5501504201yx x(2)18元11(3)当22x =时,w 有最大值3200元.17.(1)240y x =-+ (2)()()1411044541118x x p x x⎧+≤≤⎪⎪=⎨⎪+≤≤⎪⎩ (3)当产品销售单价为6.5万元时,销售场次是第10场和第18场(4)在这18场产品促销会中,第11场获得的利润最大,最大利润约为74万元18.(1)101000x -+(2)max 11250w =元。
26.3.3实际问题与二次函数(桥洞问题)
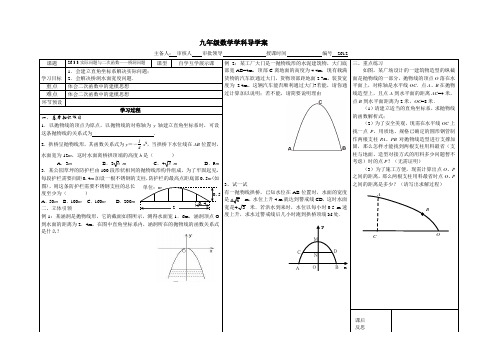
九年级数学学科导学案主备人: 审核人 审批领导 授课时间 编号 2612课题26.3.3实际问题与二次函数——桥洞问题课型 自学互学展示课例2:某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m ,顶部C 离地面的高度为4.4m ,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m ,装货宽度为 2.4m 。
这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.3、试一试有一抛物线拱桥,已知水位在AB 位置时,水面的宽度是 m ,水位上升4 m 就达到警戒线CD ,这时水面宽是 米.若洪水到来时,水位以每小时0.5 m 速度上升,求水过警戒线后几小时淹到拱桥顶端M 处.三、重点练习如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O 落在水平面上,对称轴是水平线OC .点A 、B 在抛物线造型上,且点A 到水平面的距离AC =4米,点B 到水平面距离为2米,OC =8米.(1)请建立适当的直角坐标系,求抛物线的函数解析式;(2)为了安全美观,现需在水平线OC 上找一点P ,用质地、规格已确定的圆形钢管制作两根支柱P A 、PB 对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P ?(无需证明)(3)为了施工方便,现需计算出点O 、P 之间的距离,那么两根支柱用料最省时点O 、P 之间的距离是多少?(请写出求解过程)学习目标 1.会建立直角坐标系解决实际问题; 2.会解决桥洞水面宽度问题.重点 体会二次函数中的建模思想 难点体会二次函数中的建模思想环节预设学习过程一、基本知识练习1.以抛物线的顶点为原点,以抛物线的对称轴为y 轴建立直角坐标系时,可设这条抛物线的关系式为 . 2.拱桥呈抛物线形,其函数关系式为y =-14 x 2,当拱桥下水位线在AB 位置时,水面宽为12m ,这时水面离桥拱顶端的高度h 是( )A .3mB .2 6 mC .4 3 mD .9m 3.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5m (如图),则这条防护栏需要不锈钢支柱的总长度至少为( ) A .50m B .100m C .160m D .200m 二、立体引领例1:某涵洞是抛物线形,它的截面如图所示,测得水面宽1.6m ,涵洞顶点O 到水面的距离为2.4m ,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?课后 反思2 0.5 0.4单位:m 4634ON MC D AB x yCABO。
人教版初中数学九年级上册第二十二章22.3.2实际问题与二次函数——商品利润问题

人教版数学九年级上册某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价180006000为每件40元,则每星期销售额是元,销售利润元.数量关系(1)销售额= 售价×销售量;(2)利润= 销售额-总成本=单件利润×销售量;(3)单件利润=售价-进价.例1某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?涨价销售①每件涨价x元,则每星期售出商品的利润y元,填空:单件利润(元)销售量(件)每星期利润(元)正常销售涨价销售2030020+x300-10x y=(20+x)(300-10x)建立函数关系式:y=(20+x)(300-10x),即:y=-10x2+100x+6000.60001.自变量x 的取值范围如何确定?营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.2.涨价多少元时,利润最大,最大利润是多少?y =-10x 2+100x +6000,当时,y =-10×52+100×5+6000=6250.10052(10)x =-=⨯-即定价65元时,最大利润是6250元.例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?降价销售①每件降价x元,则每星期售出商品的利润y元,填空:单件利润(元)销售量(件)每星期利润(元)正常销售降价销售2030020-x300+18x y=(20-x)(300+18x)建立函数关系式:y=(20-x)(300+18x),即:y=-18x2+60x+6000.6000综合可知,应定价65元时,才能使利润最大.1.自变量x 的取值范围如何确定?营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.2.降价多少元时,利润最大,是多少?当时,6052(18)3x =-=⨯-即定价57.5元时,最大利润是6050元.即:y =-18x 2+60x +6000,25518()6060006050.33y =-⨯+⨯+=由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:单件利润(元)销售量(件)每月利润(元)正常销售涨价销售1018010+x180-10x y=(10+x)(180-10x)1800建立函数关系式:y=(10+x)(180-10x),即:y=-10x2+80x+1800.营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x ≥0,因此自变量的取值范围是x ≤18.③涨价多少元时,利润最大,最大利润是多少?y =-10x 2+80x +1800= -10(x-4)2+1960.当x =4时,即销售单价为34元时,y 取最大值1960元.答:当销售单价为34元时,该店在一个月内能获得最大利润1960元.②自变量x的取值范围如何确定?求解最大利润问题的一般步骤1.建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”2.结合实际意义,确定自变量的取值范围;3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.例2 某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?解:由题意得:当40≤x≤50时,Q = 60(x-30)= 60x-1800∵y= 60 > 0,Q随x的增大而增大= 50时,Q最大= 1200∴当x最大答:此时每月的总利润最多是1200元.(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x 是多少元时,该商店每月获利最大,最大利润是多少元?解:当50≤x ≤70时,设y 与x 函数关系式为y =kx +b ,∵线段过(50,60)和(70,20).50k +b =6070k +b =20∴∴y =-2x +160(50≤x ≤70)解得:k =-2b = 160∴y=-2x+160(50≤x≤70)∴Q=(x-30)y=(x-30)(-2x+ 160)=-2x2+ 220x-4800=-2(x-55)2+1250 (50≤x≤70)∵a = -2<0,图象开口向下,∴当x= 55时,Q= 1250最大∴当售价在50~70元时,售价x是55元时,获利最大,最大利润是1250元.解:∵当40≤x ≤50时,Q 最大= 1200<1218当50≤x ≤70时,Q 最大= 1250>1218∴售价x 应在50~70元之间.∴令:-2(x -55)2+1250=1218解得:x 1=51,x 2=59当x 1=51时,y 1=-2x +160=-2×51+160= 58(件)当x 2=59时,y 2=-2x +160= -2×59+160= 42(件)∴若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?解:Q与x的函数关系式为:60x-1800 (40≤x≤50 )Q =-2(x-55)2+ 1250 (50≤x≤70)由例3可知:若40≤x≤50,则当x=50时,Q= 1200最大= 1250若50≤x≤70,则当x=55时,Q最大∵1200<1250∴售价x是55元时,获利最大,最大利润是1250元.(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x 的取值范围;解:①当40≤x≤50时,= 1200<1218,∵Q最大∴此情况不存在.60x-1800 (40≤x≤50 )Q =-2(x-55)2+ 1250 (50≤x≤70)②当50≤x ≤70时,Q 最大= 1250>1218,令Q = 1218,得-2(x -55)2 +1250=1218解得:x 1=51,x 2=59由Q = -2(x -55)2+1250的图象和性质可知:当51≤x ≤59时,Q≥1218∴若该商品所获利润不低于1218元,则售价x 的取值范围为51≤x ≤59.x Q 055121859511250(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?解:由题意得:51≤x≤5930 (-2 x +160)≥1620解得:51≤x≤53∵Q =-2(x -55)2+1250的顶点不在51≤x ≤53范围内,又∵a =-2<0,∴当51≤x ≤53时,Q 随x 的增大而增大∴当x 最大= 53时,Q 最大= 1242∴此时售价x 应定为53元,利润最大,最大利润是1242元.x Q 055124253511.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x 元(20 ≤x ≤30)出售,可卖出(300-20x )件,使利润最大,则每件售价应定为元.252.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y (件)与衬衣售价x (元)之间的函数关系式为.每月利润w (元)与衬衣售价x (元)之间的函数关系式为.(以上关系式只列式不化简).y =2000-5(x -100)w =[2000-5(x -100)](x -80)3.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?w =[12+2(x -1)][80-4(x -1)]=(10+2x )(84-4x )=-8x 2+128x +840=-8(x -8)2+1352.解:设生产x 档次的产品时,每天所获得的利润为w 元,则当x=8时,w 有最大值,且w 最大=1352.答:该工艺师生产第8档次产品,可使利润最大,最大利润为1352.xy 516O 74. 某种商品每天的销售利润y (元)与销售单价x (元)之间满足关系:y=ax 2+bx -75.其图象如图.(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?解:(1)由题中条件可求y =-x 2+20x -75∵-1<0,对称轴x =10,∴当x =10时,y 值最大,最大值为25.即销售单价定为10元时,销售利润最大,为25元;(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?(2)由对称性知y=16时,x=7和13.故销售单价在7 ≤x ≤13时,利润不低于16元.求解最大利润问题的一般步骤1.建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”2.结合实际意义,确定自变量的取值范围;3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.。
九下数学课件利用二次函数解决实际问题中的最值问题(课件)

【归纳总结】
最大值问题的一般步骤:
(1)利用应用题中已知条件和学过有关数学公式列出关系数;
(2)把关系式转化为二次函数的关系式;
(3)求二次函数的最大值或最小值.
知识点一 根据文字语言解决问题
【变式1】某工厂2019年产品的产量为100吨,该产品产量的年平均增长
率为x(x>0),设2021年该产品的产量为y吨,则y关于x的函数表达式为
解:设药店每天获得的利润为W元,由题意得
W=(x-50)(-2x+220)=-2(x-80)2+1 800.
∵-2<0,
∴当x=80时,W有最大值,最大值是1 800.
答:每桶消毒液的销售价定为80元时,药店每天获得的利润最大,最
大利润是1 800元.
知识点二 根据函数的图像解决问题
【变式2】一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场
k=-500,
解得
5k+b=9 500,
b=12 000.
∴y=-500x+12 000.
知识点二 根据函数的图像解决问题
(2)在销售过程中要求售价不低于进价,且不高于15元/件.若某一周该商品的销
售量不少于6 000件,求这一周该商场销售这种商品获得的最大利润和售价
分别为多少?
解:根据“在销售过程中要求售价不低于进价,且不高于 15 元/
随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售
策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销
售量y(件)与售价x(元/件)满足如图所示的函数关系(其中40≤x≤70,且x为整
数).
(1)写出y与x的函数表达式;
知识点二 根据函数的图像解决问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选]10KV线路的过流保护是该线路的()。A.近后备保护B.远后备保护C.主保护 [单选,A2型题,A1/A2型题]正常情况下血浆葡萄糖去路不包括()A.组织细胞能量来源B.合出 [单选]当前,我国开放式基金已经构建一条()在内的风险由低到高的产品线,以满足不同风险偏好者的需求。A.债券基金、货币市场基金、混合基金、股票基金B.货币市场基金、债券基金、混合基金、股票基金C.债券基金、货币市场基金、混合基金、股票基金D.货币市场基金、债券基金、股票 [多选]入境邮寄物有下列情况之一的,检验检疫机构将作退回或销毁处理。()A.带有规定禁止邮寄进境的B.证单不全的C.在限期内未办理检疫审批或报检手续的D.经检疫不合格又无有效处理方法的 [单选,A2型题,A1/A2型题]治疗花粉症最有效的方法是()。A.鼻腔应用糖皮质激素B.翼管神经切断等手术C.免疫疗法D.避免与变应原接触E.免疫源的检测 [单选]根据《担保法》规定,必须由第三人为当事人提供的担保方式是()。A.保证B.抵押C.质押D.留置 [单选,A2型题,A1/A2型题]以下自杀的相关因素不正确的是()A.重大的负性应激事件可能成为自杀的直接原因或诱因B.独身、离婚、丧偶者自杀率高于婚姻状况稳定者C.从事专门职业的医生、律师、作家、音乐家等的自杀率低于普通人群D.西方国家的自杀率大多是男多于女,而我国则相差不大 [单选]当遇到深度访谈或对问题所知不多时常用()A.专题调查B.定量调查C.半定量调查D.定性调查E.以上都不是 [单选]哪项不是早产原因()A.子宫畸形B.宫颈内口松弛C.胎儿生长受限D.妊娠期高血压疾病E.前置胎盘 [单选]石油凝固点高低与其()量有关。A.蜡B.胶质C.硫D.碳 [单选]下列的会计恒等式,不正确的是()。A.资产=权益=债权人权益+所有者权益B.资产=负债+所有者权益C.所有者权益=资产+负债D.收入一费用=利润 [单选]静止卫星通信的日凌中断发生在()A.卫星处在地球和太阳之间的连线上B.地球处在卫星和太阳之间的连线上C.每天中午12点 [单选,A2型题,A1/A2型题]下列描述的微生物特征中不正确的是()A.分布广泛B.体积微小C.种类繁多D.需借助光学显微镜或电子显微镜观察E.只能在活细胞内生长繁殖 [单选,A2型题,A1/A2型题]以下关于关节运动,错误的是()A.关节组成骨相互靠近,角度减小称为"屈"B.关节骨向腹侧面靠近者为"内收"C.骨绕矢状轴做旋转运动,骨的前面向内旋转称为"旋内"D.内收与外展相对E.部分肢体摄影位置需要关节呈一定运动状态 [单选,A1型题]关于β内酰类抗生素抗菌作用机制的描述哪项错误()。A.抑制菌细胞壁黏肽合成酶B.触发细菌的自溶酶活性C.抑制细菌的自溶酶活性D.阻碍菌细胞壁黏肽合成E.菌体膨胀变形 [单选]()是我国经济与社会发展的基本国策,也是投资建设必须贯彻执行的基本政策。A.永续发展B.可持续发展C.稳步发展D.健康发展 [单选]初孕妇,平素月经规律,孕42周,近2天胎动减少,NST无反应型,宫颈Bishop评分6分,首选的正确处理方法是()A.立即行剖宫产术B.吸氧继续观察C.做OCTD.人工破膜,了解羊水性状E.次日复查NST [单选]接种麻疹疫苗的常见反应为()A.发热B.皮疹C.嗜睡D.局部红肿E.轻微腹泻 [单选]关于传染病感染过程的各种表现,下列哪种说法是正确的()A.隐性感染极为少见B.病原体感染必引起发病C.每个传染病都存在潜伏性感染D.显性感染的传染病不过是各种不同的表现之一,而不是全部E.病原体必引起炎症过程和各种病理改变 [问答题,简答题]电力需求侧管理的内容是什么? [单选]配送网络的处理对象是()A.商流B.信息流C.物流D.资金流 [单选]要复制一个被选中的对象用什么:()A.Ctrl+移动B.Shift+移动C.Alt+移动D.Ctrl+Alt+移动 [单选]区别行政违法与行政不当时,行政违法对应的行为是裁量行为和()。A.意志行为B.羁束行为C.客观行为D.主观行为 [问答题,简答题]中国电信转型新阶段的战略目标是什么? [单选,A2型题,A1/A2型题]休克时最能反映组织和细胞是否缺氧、缺氧程度、休克是否好转与恶化的主要实验室检查是()。A.动脉血pH值B.动脉血乳酸水平C.血清钾离子浓度D.血清乳酸脱氢酶含量E.动脉血二氧化碳结合力 [单选,A2型题,A1/A2型题]A型献血者与受血者作交叉配血试验,主侧不发生凝集,次侧发生凝集,受血者的血型应为()A型B型C.AB型D.O型E.孟买型 [单选]话务员在受理业务时,回答问题要热情、(),不能用讨厌生硬的语调。A、随意B、简单C、严肃D、耐心 [单选]受皮区的血液供应影响皮肤移植成活,以下哪项是错误的()A.颜面部血供好,植皮较易成活B.胫前部血供好,植皮较易成活C.陈旧性肉芽创面血供差,游离植皮成活率低D.老年人或糖尿病患者受皮区血供较一般差,皮肤移植成活率低E.放射性损伤创面除表面损伤外有深部组织损害, [单选,A4型题,A3/A4型题]女,45岁,间歇上腹隐痛、饱胀不适6年,查体无异常。胃镜检查胃窦粘膜稍苍白,变薄,可透见粘膜下紫蓝色血管网。最可能的诊断为()A.慢性浅表性胃炎B.慢性萎缩性胃炎C.慢性肥厚性胃炎D.瘢痕期胃溃疡E.早期胃癌 [单选,A2型题,A1/A2型题]中性粒细胞碱性磷酸酶染色积分明显增加,临床上最常见于下列哪种疾病()A.类白血病反应B.慢性粒细胞白血病C.病毒感染D.恶性淋巴瘤E.急性淋巴细胞白血病 [单选]关于非孕期成人正常子宫,下列说法错误的是()。A.子宫长7~8cmB.子宫容积约50mLC.子宫体位于骨盆腔中央D.子宫颈与子宫体相连处称为峡部,长约1cmE.正常子宫呈前倾前屈位 [问答题,简答题]装置检修后,重新开工,发现新上的某台离心泵出口压力达不到工艺要求,且振动大,问哪些原因可引起以上现象?应怎样排除? [单选]带蒂的子宫浆膜下肌瘤常易误诊为()A.子宫腺肌瘤B.阔韧带肿瘤C.双子宫D.卵巢肿瘤E.残角子宫 [单选]一般情况下,施肥应选择()进行。A、晴天B、雨天C、刮风天D、阴天 [判断题]常开的防火门,当发生火灾时,应具有自行关闭和信号反馈的功能。()A.正确B.错误 [单选]男性,28岁。患急性粒细胞白血病接受化学治疗,中性粒细胞0.4×10/L。近1周来高热,咳嗽脓痰,右肺闻及较多湿啰音。X线胸片见右中肺野大片密影,隐约见密度减低区域。推测肺部感染最可能的病原体是()A.肺炎链球菌B.流感嗜血杆菌C.莫拉卡他菌D.铜绿假单胞菌E.溶血性链球 [填空题]医院医疗保险管理中管理工具包括()、()、()。 [单选,A2型题,A1/A2型题]导致腱反射亢进的病损部位为()。A.脊神经后根B.脊髓前角C.脊髓后索D.锥体束E.锥体外系 [单选,A1型题]尿道损伤后,预防尿道狭窄的主要措施是()A.应用抗生素B.超短波理疗C.留置尿管7~10日D.多饮水E.定期做尿道扩张 [单选,A1型题]全口义齿个别托盘的制作下列错误的是()A.功能性印模时,个别托盘边缘线应比基托边缘线短2~3mmB.个别托盘覆盖范围尽可能大C.个别托盘与黏膜之间可预留间隙也可不预留间隙D.骨隆突处应做缓冲E.个别托盘最后应打磨抛光送回临床
