第三节康普顿效应及其解释(精)
康普顿效应及其解释

13
1.科学研究证明,光子有能量也有动量,当光子与电子碰撞时, 光子的一些能量转移给了电子.假设光子与电子碰撞前的波长为 λ, 碰撞后的波长为 λ′,则碰撞过程中( )
A.能量守恒,动量守恒,且 λ=λ′ B.能量不守恒,动量不守恒,且 λ=λ′ C.能量守恒,动量守恒,且 λ<λ′ D.能量守恒,动量守恒,且 λ>λ′
1.正误判断(正确的打“√”,错误的打“×”)
Байду номын сангаас
(1)散射光波长的变化,是入射光与物质中的自由电子发生碰撞
的结果.
(√ )
(2)光的电磁理论能够解释康普顿效应.
( ×)
×
栏目导航
5
2.一个沿着一定方向运动的光子和一个原来静止的自由电子相 互碰撞,碰撞之后电子向某一方向运动,而光子沿着另一方向散射 出去.则这个散射光子跟原来入射时相比( )
栏目导航
9
栏目导航
10
【例 1】 (多选)美国物理学家康普顿在研究石墨对 X 射线的散 射时,发现在散射的 X 射线中,除了有与入射波长 λ0 相同的成分外, 还有波长大于 λ0 的成分,这个现象称为康普顿效应.关于康普顿效 应,下列说法正确的是( )
A.康普顿效应现象说明光具有波动性 B.康普顿效应现象说明光具有粒子性 C.当光子与晶体中的电子碰撞后,其能量增加 D.当光子与晶体中的电子碰撞后,其能量减少
栏目导航
11
BD [康普顿用光子的模型成功地解释了康普顿效应,在散射过 程中 X 射线的光子与晶体中的电子碰撞时要遵循动量守恒定律和能 量守恒定律,故 B、D 正确,A、C 错误.]
栏目导航
12
对康普顿效应的三点认识 1.光电效应应用于电子吸收光子的问题;而康普顿效应应用于讨论 光子与电子碰撞且没有被电子吸收的问题. 2.假定 X 射线光子与电子发生弹性碰撞.光子和电子相碰撞时,光 子有一部分能量传给电子,散射光子的能量减少,于是散射光的波长大于 入射光的波长. 3.康普顿效应进一步揭示了光的粒子性,也再次证明了爱因斯坦光 子说的正确性.
高中物理第2章第3节康普顿效应及其解释第4节光的波粒二象性课件粤教版选修3

B [光是一种电磁波,不是机械波,故 A 选项错误;光的衍射 现象,说明光具有波动性,可以携带信息,故 B 选项正确,C、D 选 项错误.]
3.康普顿效应证实了光子不仅具有能量,而且具有动量.如图 所示给出了光子与静止电子碰撞后,电子的运动方向,则碰后光子 ()
C [光子与电子碰撞过程中,能量守恒,动量也守恒,因光子 撞击电子的过程中光子将一部分能量传递给电子,光子的能量减少, 由 E=hλc可知,光子的波长增大,即 λ′>λ,故 C 正确.]
对光的波粒二象性的理解
1.光的粒子性的含义 粒子的含义是“不连续”“一份一份”的,光的粒子即光子, 不同于宏观概念的粒子,但也具有动量和能量. (1)当光同物质发生作用时,表现出粒子的性质. (2)少量或个别光子易显示出光的粒子性. (3)频率高,波长短的光,粒子性特征显著.
二、光的波粒二象性 2.概率波 在光的干涉实验中,每个光子按照一定的概率落在感光片的某 一点上.概率大的地方落下的 光子多 ,形成 亮纹 ;概率小的地方 落下的 光子少 ,形成 暗纹.所以,干涉条纹是光子落在感光片上各 点的 概率 分布的反映.这种 概率 分布就好像波干涉时强度的分 布.从这个意义上讲,有人把对光的描述说成是概率波.
λ
二、光的波粒二象性
1.光的波粒二象性的本质 (1)光的 干涉 和 衍射 实验表明,光是一种电磁波,具有波动性. (2) 光电效应 和 康普顿效应 则表明,光在与物体相互作用时, 是以一个个 光子 的形式出现的,具有粒子性. (3)光既有 粒子性 ,又有 波动性 ,单独使用波或粒子的解释都 无法完整地描述光所有的 性质 ,这种性质称为波粒二象性.
康普顿效应及其解释
康普顿效应
[例1]
频率为ν的光子,具有的能量为hν,将这个光
子打在处于静止状态的电子上,光子将偏离原来的运动方 向,这种现象称为光的散射。散射后的光子 A.虽改变原来的运动方向,但频率保持不变 B.光子将从电子处获得能量,因而频率将增大 C.散射后的光子运动方向将与电子运动方向在一条 直线上,但方向相反 D.由于电子受到碰撞,散射后的光子频率低于入射 光的频率 ( )
对康普顿效应的理解
1.康普顿效应现象 用 X 射线照射物体时, 散射出来的 X 射线的波长会变长 的现象称为康普顿效应。 2.康普顿效应的经典解释 单色电磁波作用于比波长尺寸小的带电粒子上时,引起 受迫振动,向各方向辐射同频率的电磁波。 经典理论解释频率不变的一般散射可以,但对康普顿效 应不能作出合理解释。
考向一 考向二
第三节
康普顿效应及其解释
1.用X射线照射物体时,一部分散射出来的X射线 的波长会 变长 ,这个现象称为康普顿效应。 2.按照经典电磁理论,散射前后光的频率 不变 , 因而散射光的波长与入射光的波长 相等 ,不应该出现 波长 变长 的散射光。 3.光子不仅具有能量,其表达式为 ε=hν ,还具
3.康普顿效应的光子理论解释 X射线为一些ε=hν的光子,与自由电子发生完全弹性 碰撞,电子获得一部分能量,散射的光子能量减少,频率 减小,波长变长。
(1)光的散射是光在介质中与物质微粒的相互作 用,使光的传播方向发生改变的现象。 (2)散射光中也有与入射光有相同波长的射线,这 是由于光子与原子碰撞,原子质量很大,光子碰撞 后,能量不变,故散射光频率不变。
[答案]
D
根据光子理论运用能量守恒和动量守恒解释康普顿 效应。理论与实验符合得很好,不仅有力的验证了光子 理论,而且也证实了微观领域的现象也严格遵循能量守 恒和动量守恒。 对康普顿现象的理解,可以类比实物粒子的弹性碰 撞,在散射过程中要遵守动量守恒和能量守恒。
15-3 康普顿效应
Il 较大 I l0
二、光子论对康普顿效应的解释
1. 经典物理遇到的困难 • 根据经典电磁波理论,当电磁波通过物质时,物 质中带电粒子将作受迫振动,其频率等于入射光 频率,所以它所发射的散射光频率应等于入射光 频率: l 0 o 在 • 电磁波为横波, j 90 方向无散射波 经典物理无法解释康普顿效应.
l 10.24nm
'
Ek 4.6610 J
17
44 18
o
'
在康普顿效应中,入射的 x 射线波长为 5.00×10-2nm, 求在散射角为60°方向上 散射 x 射线的波长和引起这种散射的反 冲电子所获得的动能。
h l l0 (1 cos ) m0c h 2.43 1012 m m0c
E p c E
2 2 2
2 0
E0 0 ,
E h h p c c l
E pc
“波粒二象性”
借用经典“波”和“粒子” 术语,但既不是经典波,又 不是经典粒子
描述光的 粒子性
IA IN
2
E h
p h
描述光的 波动性
l
N A2
振幅越大,表示光子数越多, 光子到达该处概率越大
—— 概率波
1.波长为0.710Ǻ的X射线投射到石墨上,在与入射方向 成45o角处,观察到康普顿散射的波长变化为多少Ǻ? A. √ 0.0071 B. 0.071 C. 0.036 D. 0.703 2.波长为=0.0708nm的x射线,在石蜡上受到康普顿散射, 则在方向上所散射的x射线的波长为 :
)m0c 2.0410 ( J )
2
14
Ek l0
hc
康普顿效应
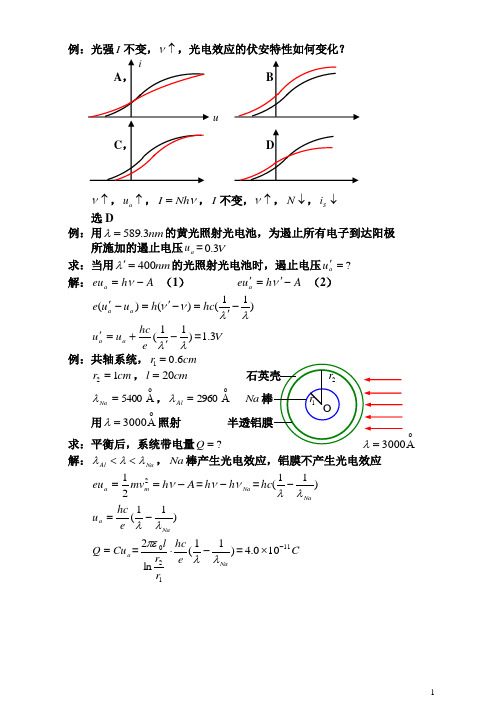
1例:光强I 不变,↑ν,光电效应的伏安特性如何变化?u↑ν,↑a u ,νNh I =,I 不变,↑ν,↓N ,↓S i选D例:用nm 3.589=λ的黄光照射光电池,为遏止所有电子到达阳极 所施加的遏止电压a u =V 3.0求:当用nm 400='λ的光照射光电池时,遏止电压?='au 解:A h eu a -=ν (1) A h u e a-'='ν (2) )11()()(λλνν-'=-'=-'hc h u u e a a)11(λλ-'+='e hc u u a a=V 3.1 例:共轴系统,cm r 6.01=cm r 12=,cm l 20= A=5400Na λ,A =2960Al λ Na 用A =3000λ照射 求:平衡后,系统带电量?=QA 解:Na Al λλλ<<,Na 棒产生光电效应,铝膜不产生光电效应221m a mv eu =A h -=ν=Na h h νν-=)11(Na hc λλ- )11(Naa e hc u λλ-=a Cu Q ==)11(ln 2120Na e hc r r l λλπε-⋅=C 11100.4-⨯2第3节 康普顿效应(1) 光致发光(2)光电效应(3)康普顿效应(4)产生正负电子对光子能量增加 一、 实验规律φ:散射角1、∀φ ∃两种散射x 射线⎩⎨⎧λ>λλ=λ康普顿散射瑞利散射::002、对于康普顿散射0λλ>波长改变量)(0φλλλf =-=∆,↑φ,↑∆λ λ∆与散射体物质种类无关,与0λ无关3、康普顿散射的相对强度与散射体的原子量有关 原子量较大,康普顿散射相对较弱 原子量较小,康普顿散射相对较强 二、 经典解释带电粒子的振动频率=入射电磁波的频率=辐射电磁波的频率 三、 光量子理论对康普顿效应的解释散射过程是光子与散射体中电子弹性碰撞,动量守恒,能量守恒 光子与自由电子碰撞,光子能量↓,↓ν,↑λ:康普顿散射光子与束缚较紧的电子碰撞,光子能量不变,波长不变:瑞利散射 原子量较小时,几乎每一个电子都可视为自由电子 康普顿散射相对较强原子量较大时,原子核对内层电子束缚较紧,只是 对外层电子束缚较弱,康普顿散射相对较弱动量守恒:00n h λ=e P n h +λ, 00n h λe P n h=-λ能量守恒:=+00E hc λE hc +λ, -0λhc E E hc =+0λ20222202cos 2eP h h h =-+φλλλλ,220222222022cos 2e P c c h c h c h =-+φλλλλ222022000022222222)(22e P c E E E E hchcc h c h c h +==+-+-+λλλλλλ2mc E =3=-)cos 1(2022φλλc h 200)(2c m hchc λ-λ=2000)(2c m hc λλλλ- 2sin 2)cos 1(2000φφλλλc m h c m h =-=-=∆令cm h c 0=λ, 2s i n 220φλλλλc=-=∆ c m hc 0=λ= A =⨯⨯⨯⨯--024.01031011.91063.683134:电子的康普顿波长 2πφ=,c c λφλλ==∆2sin 22c λ:垂直入射线方向上散射x 射线的波长改变量20c m hc =λ,c cm h λλ==0 c λ:能量等于电子静止能量的光子的波长↑φ,↑∆λ,πφ≤≤0,c λλ20≤∆≤ 0=φ,0=∆λ,πφ=,c λλ2=∆λ∆仅与φ角有关,与散射体物质种类无关,与0λ无关例:用A =20.00λ的x 射线与自由电子碰撞, 在 90=φ方向观察x 射线 求:(1)散射x 射线的波长(2)反冲电子的动能 (3)反冲电子的动量解:(1)2πφ=,c c λλλλλ==-=∆2sin 220A =+=+=224.0024.020.00c λλλ(2)=+00E hcλE hc +λ,J hc hc E E E k 15001007.1-⨯=-=-=λλ (3)00n h λ=e P n h +λ, 00n h P e λ=n h λ-,222022λλh h P e +=22011λλ+=h P e =1231044.4--⨯kgms224.02.0//00===λλλλθh h tg , 8.41=θ4 例:对于康普顿效应,证明ννννφ002022)(2sin h c m -=动量守恒:00n c h ν=e P n ch+ν, 00n h νe P c n h =-ν 能量守恒:=+00E h νE h +ν, -0νh E E h =+0ν220222202cos 2e P c h h h =-+φνννν222020*********)(22e P c E E E h h h h h +=+ν-ν+νν-ν+ν=-)cos 1(202φννh 200)(2c m h νν- ννννφ002022)(2sin h c m -=第4节 氢原子光谱 玻尔理论一、 氢原子光谱422-=n n B λ,∞=,,5,4,3 nA =7.3645B αH βH γH ∞H∞→n ,B =∞λ巴耳末系,∞H :线系极限B =∞λ=A 7.3645:线系极限波长波数ν~:沿波线单位长度内波的个数 cνλν==1~λ )121()121(4)41(1411~2222222nR n B n B n n B -=-=-=-==λν ,5,4,3=n里德伯公式1710096776.14-⨯==m BR :里德伯恒量帕邢系:)131(1~22n R -==λν, ,6,5,4=n 2mc E =c。
19-03康普顿效应
c
c
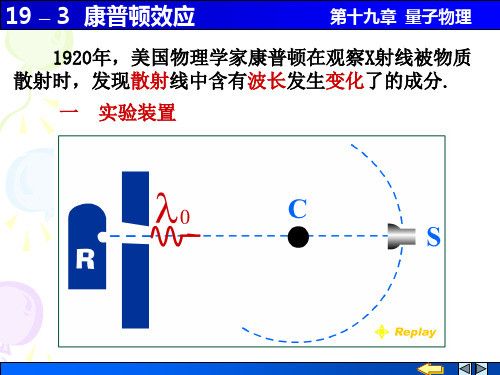
h 2h 2θ λ = (1 cosθ ) = sin m0c m0c 2
h 康普顿波长 λC = = 2.43 × 10 12 m = 2.43 × 10 3 nm m0 c
19 – 3
康普顿效应的解释
康普顿效应
第十九章 量子物理
最后得到: 最后得到:
2h 2 2 λ = λ λ0 = sin = 2λc sin m0c 2 2 h 12 电子的康普顿波长 康普顿波长。 λc = = 2.43×10 m 电子的康普顿波长。 m0c
此式说明:波长改变与散射物质无关, 此式说明:波长改变与散射物质无关,仅决定于散 射角;波长改变随散射角增大而增加。 射角;波长改变随散射角增大而增加。 计算的理论值与实验值符合得很好。 计算的理论值与实验值符合得很好。
19 – 3
康普顿效应
第十九章 量子物理
h 康普顿公式 λ = (1 cosθ ) = λC (1 cosθ ) m0 c
(3)结论 ) 散射光波长的改变量
λ 仅与 θ 有关
θ = 0, λ = 0
θ = π, (λ ) max = 2λC
散射光子能量减小
hν0 e0 c
hν y e c
e θ
λ > λ0 ,ν < ν 0
e0
x
mv
19 – 3
康普顿效应
第十九章 量子物理
h 康普顿公式 λ = (1 cosθ ) = λC (1 cosθ ) m0 c
19 – 2h 康普顿效应 3 2φ 2 φ
λ = m0 c sin 2 = λc 2 sin 2
= λc (1 cos φ )
证明了光的粒子性, 第十九章 量子物理 将光视为光子流是正确的
第四章 第3节 光的波粒二象性

解析:光既具有粒子性,又具有波动性,大量的光子波动性比 较明显,个别光子的粒子性比较明显,故 A 正确;在光的波 粒二象性中,频率越大的光其粒子性越显著,频率越小的光其 波动性越显著,故 B 正确;光在传播时往往表现出波动性, 光在跟物质相互作用时往往表现出粒子性,故 C 正确;光的 波粒二象性是指光有时表现为波动性,有时表现为粒子性,二 者是统一的,故 D 错误。 答案: D
2.下面关于光的波粒二象性的说法中,不正确的是 ( ) A.大量光子产生的效果往往显示出波动性,个别光子产 生的效果往往显示出粒子性 B.频率越大的光其粒子性越显著,频率越小的光其波动 性越显著 C.光在传播时往往表现出波动性,光在跟物质相互作用 时往往表现出粒子性 D.光不可能同时既具有波动性,又具有粒子性
对康普顿效应的理解
[例 1] 康普顿研究 X 射线经物质散射的实验,进一步证 实了爱因斯坦的光子概念。康普顿让一束 X 射线投射到一块 石墨上发生散射,测定不同散射方向上 X 射线的波长情况。 结果在散射的各个方向上测到了波长比原来更长的 X 射线。 这种改变波长的散射实验被称为康普顿效应。试用光子的概念 和能量守恒的概念解释这种波长变长的现象。
磁波 份 光 子 既有波动性又 组成的 有粒子性
2.对光的波粒二象性的理解
实验基础
表现说明Βιβλιοθήκη 1.光是一种概率波,即 1.光的波动性是光子 光子在空间各点出现的 本身的一种属性,不
光的波 干涉和 可能性大小(概率)可用 是光子之间相互作
动性 衍射
波动规律来描述。
用产生的。
2.足够能量的光在传播 2.光的波动性不同 时,表现出波的性质。 于宏观观念的波。
光的粒 子性
光电效 应、康普
顿效应
大学物理(15.3.2)--康普顿效应

Quantum Physics
第三讲 应
康普顿效
Compton Effect
康普顿 pton(1892---1962) 美国实验物理学家,芝加哥大学教授。 因发现康普顿效应而获得 1927 年诺贝尔物理学
奖
一、康普顿效应的实验及其规律
1 、实验装置
K-
X
射
0
自由 电子
1) 入射光子与外层电子弹性碰撞
外层 电子
受原子核束缚较弱 动能<<光子能量
近似自由 近似静止
静止 自由电 子
三、康普顿效应的理论解释
光子理论解释 1) X 射线由 h的光子组成;
2) 光子与实物粒子一样,能与电子等粒子作弹性碰撞。
0
0
0
自由 电子
原子
2) X 射线光子和原子内层电子相互作用
方向成
角的方向上观察,
内层电子被束缚很紧,光子相当于和整个原子发生碰撞。 光子质量远小于原子质量,碰撞时光子不会明显损失能量, 波长不变。
三、康普顿效应的理论解释
光子理论解释 1) X 射线由 h的光子组成;
2) 光子与实物粒子一样,能与电子等粒子作弹性碰撞。
0
自由 电子
结论
波长变化 X 光子
0
p 0
hν0 c
e0
p
hν c
en
碰撞过程中动量守恒
e
x
hν0 c
e0
hν c
en
mv
hν0 c
hν c
cos
mv cos
,
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节康普顿效应及其解释
基础知识
1.用X射线照射物体时,散射出的X射线的波长会,这个现象称为.
2.康普顿效应再次证明了爱因斯坦光子假说的,它不仅证明了光子具有能量,同时还证明了光子具有.
典型例题
λ=1埃的光子做康普顿实验.求:
例1用波长
(1)散射角ϕ=90°的康普顿散射波长是多少?
(2)分配给这个反冲电子的动能是多大?
答案:(1)1.024×10-10 m (2)291 eV
例2在康普顿散射中,入射光子波长为0.03 Å,反冲电子的速度为0.6c,求散射光子的波长及散射角.
答案:0.043Å 62.3°
基础练习
1.用强度为I、波长为λ的X射线(伦琴射线)分别照射锂(z=3)和铁(z=26),若在同一散射角下测得康普顿散射的X射线波长分别为和Fe(、>λ),它们对应的强度分别为I 和I ,则 ( )
A.λLi>λFe,λLi <λFe B.λLi=λFe,λLi=λFe C.λLi=λFe,λLi >λFe D.λLi<λFe,λLi >λFe
2.已知x光子的能量为0.6 MeV,在康普顿散射后,波长变化了20%,求反冲电子的能量。
3.波长为0.708A的x射线在石蜡上受到康普顿散射,求在90°和l80°方向上所散射的x射线波长各是多少?
4.X射线散射后波长会改变,是由于X射线光子和物质中电子的结果.
能力测试
5现有(1)波长为4 000 A的可见光;(2)波长为1 A的X射线束;(3)波长为1.88×10-2 A的γ射线束与自由电子碰撞,如从与入射角成90°角的方向去观察散射辐射,问每种情况下
(a)康普顿波长改变多少?
(b)该波长改变与原波长的比值为多少?
1。
