北京各区2019届初三数学期末汇编-代数综合题(1)

合集下载

2019年北京市各城区中考二模数学——代数与几何综合题25题汇总

2x+2交于C、D两点，其中点C在y轴上，点D的坐标为(3，).点P是y轴右侧的抛物线上一动点，过点P（3）若存在点P，使∠PCF=45°，请直接写出相应的点P的坐标.y5]5(x2+bx+c)过点数学试卷2019年北京市各城区中考二模数学——代数与几何综合题25题汇总y1、（2019年门头沟二模）25．如图25-1，抛物线y=-x2+b x+c与直线y=1y作PE⊥x轴于点E，交CD于点F.（1）求抛物线的解析式；72B CB CP E（2）若点P的横坐标为m，当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由.O N A x PB'y．．．．MP'O N A x P图1D DC F CA O EB x A O B x 3、（2019年平谷二模）25.定义：任何一个一次函数y=px+q，取出它的一次项系数p和常数项q，有序数组[p，q]为其特征数.例如：y=2x+5的特征数是[2，，同理，[a，b，c]为二次函数y=ax2+bx+c的特征数。

图25-1备用图（1）直接写出二次函数y=x2-5x的特征数是：_______________。

（2）若特征数是[2，m+1]的一次函数为正比例函数，求m的值；2、（2019年丰台二模）25.如图，经过原点的抛物线y=-x2+bx（b>2）与x轴的另一交（3）以y轴为对称轴的二次函数抛y=ax2+bx+c的图象经过A(2，m)、B(n，1)两点（其b点为A，过点P（1，2）作直线PN⊥x轴于点N，交抛物线于点B.点B关于抛物线对称轴的对中m﹥0，n<0），连结OA、OB、AB，得到OA⊥OB，S的特征数．△AOB=10，求二次函数y=ax2+bx+c称点为C.连结CB，CP.（1）当b=4时，求点A的坐标及BC的长；（2）连结CA，求b的适当的值，使得CA⊥CP；（3）当b=6时，如图△2，将CBP绕着点C按逆时针方向旋转，得到△C B’P’，CP与抛物线对称轴的交点为E，点M为线段B’P’（包含端点）上任意一点，请直接写出线段EM长度的取值范围.4、(2019年顺义二模)25．如图，在平面直角坐标系xOy中，抛物线y=3中，射线 l: y = 3x (x ≥ 0).点 A 是第一象限内一定点，OA = 4 3 ，射线 OA 与射线 l 的MA(1,0) ，B(0, 3) ，这条抛物线的对称轴与 x 轴交于点 C ，点 P 为射线 CB 上一个动点（不与点 C 重合），点 D 为此抛物线对称轴上一点，且∠CPD = 60︒ ．（1）求抛物线的解析式；（2）若点 P 的横坐标为 △m ， PCD 的面积为 S ，求S 与 m 之间的函数关系式；（3）过点 P 作 PE ⊥DP ，连接 DE ，F 为 DE 的中点，试求线段 BF 的最小值．5、（2019 年石景山二模）25．在平面直角坐标系 xoy．．．．．夹角为 30°.射线 l 上有一动点 P 从点 O 出发，以每秒 2 3 个单位长度的速度沿射线 l 匀速运动，同时 x 轴上有一动点 Q 从点 O 出发，以相同的速度沿 x 轴正方向匀速运动，设运动时间为 t 秒.（1）用含 t 的代数式表示 PQ 的长.（2）若当 P 、Q 运动某一时刻时，点 A 恰巧在线段 PQ 上，求出此时的 t 值.（3）定义 M 抛物线：顶点为 P ，且经过 Q 点的抛物线叫做“M 抛物线”.若当 P 、Q 运动 t秒时，将△PQA 绕其某边中点旋转 180°后，三个对应顶点恰好都落在“ 抛物线”上，求此时 t 的值. 解：（1）数学试卷（3）6、（2019 年海淀二模）25. 对于半径为 r 的⊙P 及一个正方形给出如下定义：若⊙P 上存在到此正方形四条边距离都相等的点，则称⊙P 是该正方形的“等距圆”．如图 1，在平面直角坐标系 xOy 中，正方形 ABCD 的顶点 A 的坐标为（2，4），顶点 C 、D 在 x 轴上，且点 C 在点 D 的左侧.（1）当 r = 4 2 时，①在 P 1（0，-3），P 2（4，6），P 3（ 4 2 ，2）中可以成为正方形 ABCD 的“等距圆”的圆心的是；②若点 P 在直线 y = - x + 2 上，且⊙P 是正方形 ABCD 的“等距圆”，则点 P 的坐标为；（2）如图 2，在正方形 ABCD 所在平面直角坐标系 xOy 中，正方形 EFGH 的顶点 F 的坐标为（6，2），顶点 E 、H 在 y 轴上，且点 H 在点 E 的上方.①若⊙P 同时为上述两个正方形的“等距圆”，且与 BC 所在直线相切，求⊙P 在 y 轴上截得的弦长；②将正方形 ABCD 绕着点 D 旋转一周，在旋转的过程中，线段 HF 上没有一个点能成为它的 “等距圆”的圆心，则 r 的取值范围是．y H GBAEFCO Dx（2）备用图 1图 1图 2备用图 2x 是闭区间 [1,2014]上的“闭函数”吗？请判断并说明理由；（2）若一次函数 y = kx + b (k ≠ 0)是闭区间 m , n 上的“闭函数”，求此函数的表达式；5 x 2 - [ ] 5 是闭区间 a, b 上的“闭函数”，直接写出实数a ，b [ ] [ ]7、（2019 年西城二模）25.在平面直角坐标系 xOy 中，对于⊙A 上一点 B 及⊙A 外一点 P ，给出如下定义：若直线 PB 与 x 轴有公共点（记作 M ），则称直线 PB 为⊙A 的“x 关联直线”，（1）反比例函数 y =2014数学试卷记作 l PBM .[ ]（1）已知⊙O 是以原点为圆心，1 为半径的圆，点 P （0,2），①直线 l ： y = 2 ，直线 l ： y = x + 2 ，直线 l ： y = 3x + 2 ，直线 l ： y = -2 x + 2 都经1234（3）若二次函数 y = 1的值.4 5 x - 7过点 P ，在直线 l ， l ， l ， l 中，是⊙O 的“x 关联直线”的是；12 3 4②若直线 l是⊙O 的“x 关联直线”，则点 M 的横坐标 x 的最大值是；PBMM（2）点 A （2,0）,⊙A 的半径为 1，9、（2019 年东城二模）25.定义：对于数轴上的任意两点 A ，B 分别表示数 x x ，用 x - x1, 2 1 2表示他们之间的距离；对于平面直角坐标系中的任意两点 A( x , y ), B( x , y ) 我们把1 12 2①若 P （-1,2）,⊙A 的“x 关联直线” l当 x 最大时，求 k 的值；M②若 P 是 y 轴上一个动点，且点 P的纵坐标 y > 2 ，⊙A 的两条“x 关联pPBM： y = kx + k + 2 ，点 M 的横坐标为 x ，Mx - x + y - y 叫做 A ，B 两点之间的直角距离,记作 d （A ，B ）．1 2 1 2（1）已知 O 为坐标原点，若点 P 坐标为（－ 1，3），则 d (O,P )＝_____________; （2）已知 C 是直线上 y ＝x ＋2 的一个动点，①若 D （1，0），求点 C 与点 D 的直角距离的最小值；②若 E 是以原点 O 为圆心，1 为半径的圆上的一个动点，请直接写出点 C 与点 E 的直角距离的最小值．直线”lPCM, l PDN是⊙A 的两条切线，切y点分别为 C ,D ，作直线 CD 与 x 轴点于点 E ，当点 P 的位置发生变化时， AE 的长度是否发生改变？并说明理由.8、（2019 年通州二模）24．设 a ，b 是任意两个不等实数，我们规定：满足不等式a ≤ x ≤ b的实数 x 的所有取值的全体叫做闭区间，表示为 a, b . 对于一个函数，如果它的自变量 x 与函数值 y 满足：当 m ≤ x ≤n 时，有 m ≤ y ≤n ，我们就称此函数是闭区间 m , n 上的“闭函数”.32 1-2 -1O1 2 x-1 -210、（2019 年朝阳二模）25．如图，在平面直角坐标系中 xOy ，二次函数 y =ax 2-2ax +3 的图象与 xyCA OB xC -2 -1 O A2 x大，请直接写出点 M 的坐标..轴分别交于点 A 、B ，与 y 轴交于点 C ，AB =4，动点 P 从 B 点出发，沿 x 轴负方向以每秒 1 个单位长度的速度移动．过 P 点作 PQ 垂直于直线 BC ，垂足为 Q ．设 P 点移动的时间为 t 秒（t ＞△0）， BPQ 与△ABC 重叠部分的面积为 S ．（1）求这个二次函数的关系式；（2）求 S 与 t 的函数关系式；（△3）将 BPQ 绕点 P 逆时针旋转 90°，当旋转后的△BPQ 与二次函数的图象有公共点时，求 t 的取值范围（直接写出结果）．11、（2019 年密云二模）25．按右图所示的流程，输入一个数据 x ，根据 y 与 x 的关系式就输出一个数据 y ，这样可以将一组数据变换成另一组新的数据，要使任意一组都在20～100（含 20 和 100）之间的数据，变换成一组新数据后能满足下列两个要求：（一）新数据都在 60～100（含 60 和 100）之间；（二）新数据之间的大小关系与原数据之间的大小关系一致，即原数据大的对应的新数据也较大.（1）若 y 与 x 的关系是 y ＝x ＋p(100－x)，请说明：当 p1＝ 2 时，这种变换满足上述两个要求；（2）若按关系式 y=a(x －h)2＋k (a>0)将数据进行变换，请写出一个满足上述要求的这种关系式（不要求对关系式符合题意作说明，但要写出关系式得出的主要过程）12、（2019 年延庆二模）13 、 (2019 年房山二模 )25. 如果一条抛物线说明理由；（3）在（2）的条件下，若以点 E 为圆心，r 为半径的圆与线段 AD 只有一个公共点，求出 r 的取值范围．14、（2019 年昌平二模）25．如图，已知点A （1，0），B （0，3），C （-3，0），动点 P （x ，y ）在线段 AB 上，CP 交 y y轴于点 D ，设 BD 的长为 t . B（1）求 t 关于动点 P 的横坐标 x 的函数表达式； 2（2）若 △S BCD ：△S AOB =2：1，求点 P 的坐标，并判断线段 CD 与线段 AB 的数量及位置关系，说明理由； 1（3）在（2）的条件下，若 M 为 x 轴上的点，且∠BMD 最-115、（2019 年怀柔二模）25.在平面直角坐标系 xoy 中，已知 A(3，0)、B(1，2)，直线 l 围绕△OAB 的顶点 A 旋转，与 y 轴相交于点 P.探究解决下列问题：（1）在图 1 中求△OAB 的面积.（2）如图 1 所示，当直线 l 旋转到与边 OB 相交时，试确定点 P 的位置，使顶点 O 、B 到直线 l 的距离之和最大，并简要说明理由.（3）当直线 l 旋转到与 y 轴的负半轴相交时，在图 2 中试确定点 P 的位置，使顶点 O 、B 到直线 l 的距离之和最大，画出图形并求出此时 P 点的坐标. （点 P 位置的确定只需作出图形，不用证明）.y =ax 2 +bx +c (a ≠ 0)与 x 轴有两个交点，那么以该抛物线yyB的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．（1）“抛物线三角形”一定是三角形；lPBO Ax（2）如图，△ OAB 是抛物线 y =-x 2 +b x (b >0)的“抛物线 x三角形”，是否存在以原点 O 为对称中心的矩形 ABCD ？若存在，求出过 O 、C 、D 三点的抛物线的表达式；若不存在，O A图 1图 2x-2+1的图象向左平移2个单位，再向下平移1个单位得到y=x-2+1是y与x的“反比例平移函数”．16、（2019年大兴二模）24.已知：二次函数y=x2+bx+8的图象与x轴交于点A（–2，0）．（1）求二次函数y=x2+bx+8的图象与x轴的另一个交点B及顶点M的坐标；（2）点P从点B出发，以每秒1个单位的速度沿水平方向向右运动，同时点Q从点M出发，以每秒2个单位的速度沿竖直方向向下运动，当点P运动到原点O时，P、Q同时停止运动.点C、点D分别为点P、点Q关于原点的对称点，设四边形PQCD的面积为S，运动时间为t，求S与t的函数关系表达式（不必写出t的取值范围）；（3）在（2）的运动过程中，四边形PQCD能否形成矩形？若能，求出此时t的值；若不能，请说明理由.（2）如图，在平面直角坐标系中，点O为原点，矩形OABC的顶点A、C的坐标分别为(9，0)、(0，3)．点D是OA的中点，连接OB、CD交于点E，“反比例平移函数”y=ax+k的图象经过B、E两点．则这个“反比例平移函数”的表达式x-6为；这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合，请写出这个反比例函数的表达式．（3）在（2）的条件下，已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧)，若B、E、P、Q为顶点组成的四边形面积为16，请求出点P的坐标．yC BEO D A x17、（2019年燕山二模）25.定义：如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合，那么称这个函数是y与x的“反比例平移函数”．例如:y=11x的图象，则y=1（1）若矩形的两边分别是2cm、3cm，当这两边分别增加x(cm)、y(cm)后，得到的新矩形的面积为8cm2，求y与x的函数表达式，并判断这个函数是否为“反比例平移函数”．。

2019.1海淀区初三数学期末试题及答案

2019.1海淀区初三数学期末试题及答案数学 2018．1学校姓名准考证号一、选择题（本题共16分,每小题2分）第1-8题均有四个选项,符合题意的选项只有一个． 1．抛物线()212y x =-+的对称轴是A ．1x =-B ．1x =C ．2x =-D ．2x =2．在△ABC 中,∠C =90°．若AB =3,BC =1,则sin A 的值为A ．13B ．C ．3D ．33．如图,线段BD ,CE 相交于点A ,DE ∥BC ．若AB =4,AD =2,DE =1.5, 则BC 的长为A ．1B ．2C ．3D ．4 4．如图,将△ABC 绕点A 逆时针旋转100°,得到△ADE ．若点D 在线段BC 的延长线上,则B ∠的大小为A ．30°B ．40°C ．50°D ．60°5．如图,△OAB∽△OCD ,OA :OC=3:2,∠A=α,∠C=β,△OAB 与△OCD 的面积分别是1S 和2S ,△OAB 与△OCD 的周长分别是1C 和2C ,则下列等式一定成立的是A ．32OBCD=DECBAEB C DAD OA BCB ．32αβ= C ．1232S S =D ．1232C C =6．如图,在平面直角坐标系xOy 中,点A 从（3,4）出发,绕点O 顺时针旋转一周,则点A 不经过 A ．点M B ．点N C ．点P D ．点Q7．如图,反比例函数ky x =的图象经过点A （4,1）,当1y <时,x 的取值范围是A ．0x <或4x >B ．04x <<C ．4x <D ．4x >8．两个少年在绿茵场上游戏．小红从点A 出发沿线段AB 运动到点B ,小兰从点C 出发,以相同的速度沿⊙O 逆时针运动一周回到点C ,两人的运动路线如图1所示,其中AC =DB ．两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C 的距离y 与时间x （单位：秒）的对应关系如图2所示．则下列说法正确的是图1 图2A ．小红的运动路程比小兰的长B ．两人分别在1.09秒和7.49秒的时刻相遇C ．当小红运动到点D 的时候,小兰已经经过了点D D ．在4.84秒时,两人的距离正好等于⊙O 的半径二、填空题（本题共16分,每小题2分）9．方程220x x -=的根为．10．已知∠A 为锐角,且tan A =那么∠A 的大小是 °．11．若一个反比例函数图象的每一支上,y 随x 的增大而减小,则此反比例函数表达式可以是．（写出一个即可）12．如图,抛物线2y ax bx c =++的对称轴为1x =,点P ,点Q 是抛物线与x 轴的两个交点,若点P 的坐标为（4,0）,则点Q 的坐标为．13．若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为．14．如图,AB 是⊙O 的直径,PA ,PC 分别与⊙O 相切于点A ,点C ,若∠P =60°,PA =,则AB 的长为．15．在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离．如图,在一个路口,一辆长为10m 的大巴车遇红灯后停在距交通信号灯20m 的停止线处,小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾xm,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,则x 的最小值为．停止线信号灯16．下面是“作一个30°角”的尺规作图过程．请回答：该尺规作图的依据是．三、解答题（本题共68分,第17~22题,每小题5分；第23~26小题,每小题6分；第27~28小题,每小题7分）解答应写出文字说明、演算步骤或证明过程．17．计算：2sin 30°2cos 45-° 18．已知1x =是关于x 的方程2220x mx m --=的一个根,求(2)1m m +的值．19．如图,在△ABC 中,∠B 为锐角, AB =,AC =5,sin 35C=,求BC 的长．CB A20．码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间．轮船到达目的地后开始卸货,记平均卸货速度为v （单位：吨/天）,卸货天数为t ．（1）直接写出v 关于t 的函数表达式：v = ；（不需写自变量的取值范围）（2）如果船上的货物5天卸载完毕,那么平均每天要卸载多少吨？21．如图,在△ABC 中,∠B =90°,AB =4,BC =2,以AC 为边作△ACE ,∠ACE =90°,AC =CE ,延长BC 至点D ,使CD =5,连接DE ．求证：△ABC ∽△CED ．EB C DA22．古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究：如图（图1中BAC ∠为锐角,图2中BAC∠为直角,图3中BAC ∠为钝角）．AB B' C' CAB B'(C')C B C' B' C A在△ABC 的边BC 上取B ',C '两点,使AB B AC C BAC ''∠∠∠==,则ABC △∽B BA '△∽C AC '△,()ABB BAB'=,()ACC CAC'=,进而可得22AB AC += ；（用BB CC BC ''，，表示）若AB =4,AC =3,BC =6,则B C ''= ．23．如图,函数ky x =（0x <）与y ax b =+的图象交于点A （-1,n ）和点B （-2,1）．（1）求k ,a ,b 的值；（2）直线x m =与ky x =（0x <）的图象交于点P ,与1y x =-+的图象交于点Q ,当90PAQ ∠>︒时,直接写出m 的取值范围．24．如图,A ,B ,C 三点在⊙O 上,直径BD 平分∠ABC ,过点D 作DE ∥AB 交弦BC 于点E ,在BC 的延长线上取一点F ,使得EF =DE ．（1）求证：DF 是⊙O 的切线；（2）连接AF 交DE 于点M ,若 AD =4,DE =5,求DM 的长．图1 图2 图325．如图,在△ABC中,90ABC∠=︒,40C∠=°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至AD',连接BD'．已知AB=2cm,设BD为x cm,B D'为y cm．D'B D CA小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整．（说明：解答中所填数值均保留一位小数）（1x y（2）建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象．（3）结合画出的函数图象,解决问题：线段BD'的长度的最小值约为__________cm；若BD'≥BD,则BD的长度x的取值范围是_____________．26．已知二次函数243y ax ax a =-+．（1）该二次函数图象的对称轴是x = ；（2）若该二次函数的图象开口向下,当14x ≤≤时,y 的最大值是2,求当14x ≤≤时,y 的最小值；（3）若对于该抛物线上的两点11()P x y ， ,22()Q x y ，,当1+1t x t ≤≤,25x ≥时,均满足12y y ≥,请结合图象,直接写出t 的最大值．27．对于⊙C 与⊙C 上的一点A ,若平面内的点P 满足：射线AP 与⊙C 交于点Q （点Q 可以与点P 重合）,且12PAQA ≤≤,则点P 称为点A 关于⊙C 的“生长点”．已知点O 为坐标原点,⊙O 的半径为1,点A （-1,0）．（1）若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标________；（2）若点B 是点A 关于⊙O 的“生长点”,且满足1tan 2BAO ∠=,求点B 的纵坐标t 的取值范围；（3）直线y b=+与x 轴交于点M ,与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是_____________________________．28．在△ABC 中,∠A =90°,AB =AC ．（1）如图1,△ABC 的角平分线BD ,CE 交于点Q ,请判断“QB =”是否正确：________（填“是”或“否”）；（2）点P 是△ABC 所在平面内的一点,连接PA ,PB ,且PB=PA ．①如图2,点P 在△ABC 内,∠ABP =30°,求∠PAB 的大小；②如图3,点P 在△ABC 外,连接PC ,设∠APC=α,∠BPC =β,用等式表示α,β之间的数量关系,并证明你的结论．PPEDQB CAB CAB CA图1 图2图3Equation Chapter 1 Section 1初三第一学期期末学业水平调研数学参考答案及评分标准 2018．1一、选择题（本题共16分,每小题2分）二、填空题（本题共16分,每小题2分） 9．0或2 10．60 11．1y x =（答案不唯一） 12．（2-,0）13．6 14．215．1016．三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,一条弧所对的圆周角是它所对圆心角的一半；或：直径所对的圆周角为直角,三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,直角三角形两个锐角互余；或：直径所对的圆周角为直角,1sin 2A =,A ∠为锐角,30A ∠=︒.三、解答题（本题共68分,第17~22题,每小题5分；第23~26小题,每小题6分；第27~28小题,每小题7分）17．解：原式 = 12222⨯-⨯+………………3分= 1= 1 ………………5分18．解：∵ 1x =是关于x 的方程2220x mx m --=的一个根, ∴ 2120m m --=.∴ 221m m +=. ………………3分∴2(2)211m m m m =++=. ………………5分 19．解：作AD ⊥BC 于点D ,∴ ∠ADB =∠ADC =90°.∵ AC =5,3sin 5C =,∴ sin 3AD AC C =⋅=. ………………2分 ∴ 在Rt △ACD 中,4CD =. ………………3分∵ AB= ∴ 在Rt △ABD 中,3BD ==. ………………4分∴ 7BC BD CD =+=. ………………5分 20．解：（1）240t . ………………3分（2）由题意,当5t =时,24048v t ==. ………………5分答：平均每天要卸载48吨. 21．证明：∵ ∠B =90°,AB =4,BC =2,∴AC ==. ∵ CE =AC , ∴CE = ∵ CD =5,∴ AB ACCE CD =. ………………3分∵ ∠B =90°,∠ACE =90°,∴ ∠BAC +∠BCA =90°,∠BCA +∠DCE =90°.∴ ∠BAC =∠DCE .∴ △ABC ∽△CED . ………………5分 22．BC ,BC ,()BC BB CC ''+ ………………3分116 ………………5分23．解：（1）∵ 函数ky x =（0x <）的图象经过点B （-2, 1）,EB C DA∴ 12k =-,得2k =-. ………………1分∵ 函数k y x =（0x <）的图象还经过点A （-1,n ）, ∴221n -==-,点A 的坐标为（-1,2）. ………………2分∵ 函数y ax b =+的图象经过点A 和点B ,∴ 2,2 1.a b a b -+=⎧⎨-+=⎩解得1,3.a b =⎧⎨=⎩………………4分（2）20m -<<且1m ≠-. ………………6分 24．（1）证明：∵ BD 平分∠ABC , ∴ ∠ABD =∠CBD . ∵ DE ∥AB , ∴ ∠ABD =∠BDE .∴ ∠CBD =∠BDE . ………………1分 ∵ ED =EF ,∴ ∠EDF =∠EFD . ∵∠EDF +∠EFD +∠EDB +∠EBD =180°, ∴ ∠BDF =∠BDE +∠EDF =90°.∴ OD ⊥DF . ………………2分 ∵OD 是半径,∴ DF 是⊙O 的切线. ………………3分（2）解：连接DC ,∵ BD 是⊙O 的直径, ∴ ∠BAD =∠BCD =90°. ∵ ∠ABD =∠CBD ,BD =BD , ∴ △ABD ≌△CBD . ∴ CD =AD =4,AB =BC. ∵ DE =5,∴3CE ==,EF =DE =5.∵ ∠CBD =∠BDE , ∴ BE =DE =5.∴ 10BF BE EF =+=,8BC BE EC =+=.∴ AB =8. ………………5分 ∵ DE ∥AB , ∴ △ABF ∽△MEF .∴ AB BFME EF =.∴ ME =4.∴ 1DM DE EM =-=. ………………6分25．（1）0.9. ………………1分（2）如右图所示. ………………3分（3）0.7, ………………4分00.9x ≤≤.………………6分 26．解：（1）2． ………………1分（2）∵ 该二次函数的图象开口向下,且对称轴为直线2x =, ∴ 当2x =时,y 取到在14x ≤≤上的最大值为2. ∴ 4832a a a -+=.∴ 2a =-,2286y x x =-+-. ………………3分 ∵ 当12x ≤≤时,y 随x 的增大而增大, ∴ 当1x =时,y 取到在12x ≤≤上的最小值0. ∵ 当24x ≤≤时,y 随x 的增大而减小,∴ 当4x =时,y 取到在24x ≤≤上的最小值6-.∴ 当14x ≤≤时,y 的最小值为6-. ………………4分（3）4. ………………6分 27．解：（1）（2,0）(答案不唯一). ………………1分112O（2）如图,在x 轴上方作射线AM ,与⊙O 交于M ,且使得1tan 2OAM ∠=,并在AM 上取点N ,使AM =MN ,并由对称性,将MN 关于x 轴对称,得M N '',则由题意,线段MN 和M N ''上的点是满足条件的点B .作MH ⊥x 轴于H ,连接MC ,∴ ∠MHA =90°,即∠OAM +∠AMH =90°. ∵ AC 是⊙O 的直径,∴ ∠AMC =90°,即∠AMH +∠HMC =90°. ∴ ∠OAM =∠HMC . ∴1tan tan 2HMC OAM ∠=∠=.∴12MH HC HA MH ==. 设MH y =,则2AH y =,12CH y =,∴ 522AC AH CH y =+==,解得45y =,即点M 的纵坐标为45. 又由2AN AM =,A 为（-1,0）,可得点N 的纵坐标为85,故在线段MN 上,点B 的纵坐标t 满足：4855t ≤≤. ………………3分由对称性,在线段M N ''上,点B 的纵坐标t 满足：8455t -≤≤-.………………4分 ∴ 点B 的纵坐标t 的取值范围是8455t -≤≤-或4855t ≤≤. （3）41b --≤-或14b ≤≤. ………………7分 28．解：（1）否. ………………1分（2）① 作PD ⊥AB 于D ,则∠PDB =∠PDA =90°, ∵ ∠ABP =30°, ∴12PD BP =. ………………2分∵PB =,∴2PD PA =.B∴sin PD PAB PA ∠==.由∠PAB 是锐角,得∠PAB =45°. ………………3分另证：作点P关于直线AB的对称点'P ,连接',',B P P A P P,则',',','P BA PBA P AB PAB BP BP AP AP ∠=∠∠=∠==.∵∠ABP =30°, ∴'60P BP ∠=︒. ∴△'P BP 是等边三角形. ∴'P P BP =.∵PB =,∴'P P =. ………………2分∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒,证明如下： ………………4分作AD ⊥AP ,并取AD =AP ,连接DC ,DP . ∴ ∠DAP =90°. ∵ ∠BAC =90°,∴ ∠BAC +∠CAP =∠DAP +∠CAP , 即 ∠BAP =∠CAD . ∵ AB =AC ,AD =AP , ∴ △BAP ≌△CAD .∴ ∠1=∠2,PB =CD . ………………5分∵ ∠DAP =90°,AD =AP ,∴PD =,∠ADP =∠APD =45°. ∵PB =,BC∴ PD =PB =CD . ∴ ∠DCP =∠DPC . ∵ ∠APC =α,∠BPC =β,∴ 45DPC α∠=+︒,12αβ∠=∠=-. ∴ 31802902DPC α∠=︒-∠=︒-. ∴ 139045ADP αβ∠=∠+∠=︒--=︒.∴ 45αβ+=︒. ………………7分。

2019中考数学代数综合专题试卷精选汇编(有解析答案)

代数综合专题东城区20. 已知关于x 的一元二次方程()2320x m x m -+++=.(1) 求证：无论实数m 取何值，方程总有两个实数根；(2) 若方程有一个根的平方等于4，求m 的值.20. （1）证明：()()2=+3-42m m ∆+()2=+1m∵()2+10m ≥，∴无论实数m 取何值，方程总有两个实根. -------------------2分（2）解：由求根公式，得()()1,231=2m m x +±+，∴1=1x ，2=+2x m .∵方程有一个根的平方等于4，∴()2+24m =.解得=-4m ，或=0m . -------------------5分西城区20．已知关于x 的方程2(3)30mx m x +--=（m 为实数，0m ≠）．（1）求证：此方程总有两个实数根．（2）如果此方程的两个实数根都为正整数，求整数m 的值．【解析】（1）2222(3)4(3)691269(3)0m m m m m m m m ∆=--⨯-=-++=++=+≥ ∴此方程总有两个不相等的实数根．（2）由求根公式，得(3)(3)2m m x m --±+=，∴11x =，23x m =-（0m ≠）．∵此方程的两个实数根都为正整数，∴整数m 的值为1-或3-．海淀区20．关于x 的一元二次方程22(23)10x m x m --++=.（1）若m 是方程的一个实数根，求m 的值；（2）若m 为负数．．，判断方程根的情况.20．解：（1）∵m 是方程的一个实数根，∴()222310m m m m --++=. ………………1分 ∴13m =-. ………………3分(2)24125b ac m ∆=-=-+.∵0m <，∴120m ->.∴1250m ∆=-+>. ………………4分∴此方程有两个不相等的实数根.丰台区20．已知：关于x 的一元二次方程x 2 - 4x + 2m = 0有两个不相等的实数根．（1）求m 的取值范围；（2）如果m 为非负整数．．．．，且该方程的根都是整数．．，求m 的值．20．解：（1）∵方程有两个不相等的实数根，∴Δ>0.∴Δ=24421680m m --⋅=->（）．∴2m <. ………………………2分（2）∵2m <，且m 为非负整数，∴=0m 或1. ………………………3分当m =0时，方程为240x x -=，解得方程的根为01=x ，24x =，符合题意；当m =1时，方程为2420x x -+=，它的根不是整数，不合题意，舍去.综上所述，m =0. ………………………5分石景山区20．关于x 的一元二次方程2(32)60mx m x +--=．（1）当m 为何值时，方程有两个不相等的实数根；（2）当m 为何整数时，此方程的两个根都为负整数．20．解：（1）∵24b ac ∆=-2(32)24m m =-+2(32)0m =+≥∴当0m ≠且23m ≠-时,方程有两个不相等实数根. …………… 3分（2）解方程，得： 12x m =,23x =-． …………… 4分∵m 为整数,且方程的两个根均为负整数,∴1m =-或2m =-．∴1m =-或2m =-时, 此方程的两个根都为负整数. …………… 5分朝阳区20. 已知关于x 的一元二次方程0)1(2=+++k x k x ．（1）求证：方程总有两个实数根；（2）若该方程有一个根是正数，求k 的取值范围.20. （1）证明：依题意，得k k 4)1(2-+=∆ …………………1分.)1(2-=k …………………………………2分∵0)1(2≥-k ，∴方程总有两个实数根. ………………………3分（2）解：由求根公式，得11-=x ，k x -=2. …………………………4分∵方程有一个根是正数，∴0>-k .∴0<k .………………………………5分燕山区21．已知关于x 的一元二次方程22(21)0x k x k k -+++=．（1）求证：方程有两个不相等的实数根；（2）当方程有一个根为1时，求k 的值．21．（1）证明：因为[])(14)12(4222k k k ac b +⨯⨯-+-=-01〉=所以有两个不等实根 …………3′..(2)当x=1 时，01)12(12=++⨯+-k k k02=-k k ′1021==k k 或 ………5′门头沟区22. 已知关于x 的一元二次方程22410x x k ++-=有实数根.（1）求k 的取值范围；（2）若k 为正整数，且方程有两个非零的整数根，求k 的取值.22（本小题满分5分）解：（1）由题意得，168(1)0k ∆=--≥．………………………………………1分∴3k ≤． ………………………………………2分（2）∵k 为正整数，∴123k =，，．当1k =时，方程22410x x k ++-=有一个根为零；……………………3分当2k =时，方程22410x x k ++-=无整数根； ……………………4分当3k =时，方程22410x x k ++-=有两个非零的整数根.综上所述，1k =和2k =不合题意，舍去；3k =符合题意．……………5分大兴区20. 已知关于x 的一元二次方程01632=-+-k x x 有实数根，k 为负整数．（1）求k 的值；（2）如果这个方程有两个整数根，求出它的根．20.解：（1）根据题意，得Δ=(－6)2－4×3（1－k ）≥0．解得2≥-k ．……………………………………………………………1分∵k 为负整数，∴k =－1，－2．……………………………………… 2分（2）当1=-k 时，不符合题意，舍去； ………………………………… 3分当2=-k 时，符合题意，此时方程的根为121==x x ．………… 5分平谷区20．关于x 的一元二次方程2210x x k ++-=有两个不相等的实数根．（1）求k 的取值范围；（2）当k 为正整数时，求此时方程的根．20．解：（1）∵关于x 的一元二次方程有两个不相等的实数根．∴()2Δ2410k =--> ····················1 =8－4k >0.∴2k < ··························2 （2）∵k 为正整数，∴k =1． ···························3 解方程220x x +=，得120,2x x ==-． ·············5 怀柔区20.已知关于x 的方程226990-+-=x mx m .（1）求证：此方程有两个不相等的实数根；（2）若此方程的两个根分别为x 1，x 2，其中x 1>x 2，若x 1=2x 2，求m 的值.20.(1）∵△=(-6m)2-4(9m 2-9) ……………………………………………………………………1分=36m 2-36m 2+36=36>0.∴方程有两个不相等的实数根……………………………………………………………2分（2）66332m x m ±===±.……………………………………………………3分 ∵3m+3>3m -3,∴x 1=3m+3,x 2=3m-3, …………………………………………………………………………4分 ∴3m+3=2(3m -3) .∴m=3. …………………………………………………………………………………………5分延庆区20．已知：∠AOB 及边OB 上一点C ．求作：∠OCD ，使得∠OCD=∠AOB ．要求：1．尺规作图，保留作图痕迹，不写做法；（说明：作出一个．．即可） 2．请你写出作图的依据．C B O A20．（1）作图（略） ……2分（2）到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角. ……5分顺义区20．已知关于x 的一元二次方程()21260x m x m --+-=．（1）求证：方程总有两个实数根；（2）若方程有一个根是负数，求m 的取值范围．20．（1）证明：∵()214(26)m m ⎡⎤∆=----⎣⎦221824m m m =-+-+ 21025m m =-+()25m =-≥0 …………………………………………………… 2分 ∴ 方程总有两个实数根． ………………………………………………… 3分（2）解：∵1(5)2m m x -±-==， ∴ 13x m =-，22x =． ……………………………………………… 4分由已知得 30m -<．∴ 3m <． ………………………………………………………………… 5分。

北京西城区2019年初三上年末数学试卷含解析解析

北京西城区2019年初三上年末数学试卷含解析解析【一】选择题〔此题共30分，每题3分〕下面各题均有四个选项，其中只有一个是符合题意旳、1、二次函数y=〔x﹣5〕2+7旳最小值是〔〕A、﹣7B、7C、﹣5D、52、如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，那么cosA旳值为〔〕A、B、C、D、3、如图，⊙C与∠AOB旳两边分别相切，其中OA边与⊙C相切于点P、假设∠AOB=90°，OP=6，那么OC旳长为〔〕A、12B、C、D、4、将二次函数y=x2﹣6x+5用配方法化成y=〔x﹣h〕2+k旳形式，以下结果中正确旳选项是〔〕A、y=〔x﹣6〕2+5B、y=〔x﹣3〕2+5C、y=〔x﹣3〕2﹣4D、y=〔x+3〕2﹣95、假设一个扇形旳半径是18cm，且它旳弧长是12πcm，那么此扇形旳圆心角等于〔〕A、30°B、60°C、90°D、120°6、如图，在平面直角坐标系xOy中，点A旳坐标为〔﹣1，2〕，AB⊥x轴于点B、以原点O为位似中心，将△OAB放大为原来旳2倍，得到△OA1B1，且点A1在第二象限，那么点A1旳坐标为〔〕A、〔﹣2，4〕B、〔，1〕C、〔2，﹣4〕D、〔2，4〕7、如图，一艘海轮位于灯塔P旳南偏东37°方向，距离灯塔40海里旳A处，它沿正北方向航行一段时刻后，到达位于灯塔P旳正东方向上旳B处、这时，B 处与灯塔P旳距离BP旳长能够表示为〔〕A、40海里B、40tan37°海里C、40cos37°海里D、40sin37°海里8、如图，A，B，C三点在旳圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是旳中点，连接DB，DC，那么∠DBC旳度数为〔〕A、30°B、45°C、50°D、70°9、某商品现在旳售价为每件60元，每星期可卖出300件、市场调查反映，假如调整商品售价，每降价1元，每星期可多卖出20件、设每件商品降价x元后，每星期售出商品旳总销售额为y元，那么y与x旳关系式为〔〕A、y=60〔300+20x〕B、y=〔60﹣x〕〔300+20x〕C、y=300〔60﹣20x〕D、y=〔60﹣x〕〔300﹣20x〕10、二次函数y=2x2﹣8x+m满足以下条件：当﹣2＜x＜﹣1时，它旳图象位于x 轴旳下方；当6＜x＜7时，它旳图象位于x轴旳上方，那么m旳值为〔〕A、8B、﹣10C、﹣42D、﹣24【二】填空题〔此题共18分，每题3分〕11、假设，那么旳值为、12、点A〔﹣3，y1〕，B〔2，y2〕在抛物线y=x2﹣5x上，那么y1y2、〔填“＞”，“＜”或“=”〕13、△ABC旳三边长分别为5，12，13，与它相似旳△DEF旳最小边长为15，那么△DEF旳周长为、14、如图，线段AB和射线AC交于点A，∠A=30°，AB=20、点D在射线AC上，且∠ADB是钝角，写出一个满足条件旳AD旳长度值：AD=、15、程大位所著《算法统宗》是一部中国传统数学重要旳著作、在《算法统宗》中记载：“平地秋千未起，踏板离地一尺、送行二步与人齐，五尺人高曾记、仕女佳人争蹴，终朝笑语欢嬉、良工高士素好奇，算出索长有几？”【注释】1步=5尺、译文：“当秋千静止时，秋千上旳踏板离地有1尺高，如将秋千旳踏板往前推动两步〔10尺〕时，踏板就和人一样高，那个人身高是5尺、漂亮旳小姐和才子们，每天都来争荡秋千，欢声笑语终日不断、好奇旳能工巧匠，能算出这秋千旳绳索长是多少吗？”如图，假设秋千旳绳索长始终保持直线状态，OA是秋千旳静止状态，A是踏板，CD是地面，点B是推动两步后踏板旳位置，弧AB是踏板移动旳轨迹、AC=1尺，CD=EB=10尺，人旳身高BD=5尺、设绳索长OA=OB=x尺，那么可列方程为、16、阅读下面材料：在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：尺规作图：过圆外一点作圆旳切线、：P为⊙O外一点、求作：通过点P旳⊙O旳切线、小敏旳作法如下：如图，〔1〕连接OP，作线段OP旳垂直平分线MN交OP于点C；〔2〕以点C为圆心，CO旳长为半径作圆，交⊙O于A，B两点；〔3〕作直线PA，PB、因此直线PA，PB确实是所求作旳切线、老师认为小敏旳作法正确、请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是；由此可证明直线PA，PB差不多上⊙O旳切线，其依据是、【三】解答题〔此题共72分，第17-26题，每题5分，第27题7分，第28题7分，第29题8分〕解承诺写出文字说明，演算步骤或证明过程、17、计算：4cos30°•tan60°﹣sin245°、18、如图，△ABC中，AB=12，BC=15，AD⊥BC于点D，∠BAD=30°，求tanC旳值、19、抛物线y=﹣x2+2x+3与x轴交于A，B两点，点A在点B旳左侧、〔1〕求A，B两点旳坐标和此抛物线旳对称轴；〔2〕设此抛物线旳顶点为C，点D与点C关于x轴对称，求四边形ACBD旳面积、20、如图，在四边形ABCD中，AD∥BC，∠A=∠BDC、〔1〕求证：△ABD∽△DCB；〔2〕假设AB=12，AD=8，CD=15，求DB旳长、21、某小区有一块长21米，宽8米旳矩形空地，如下图、社区打算在其中修建两块完全相同旳矩形绿地，同时两块绿地之间及四周都留有宽度为x米旳人行通道、假如这两块绿地旳面积之和为60平方米，人行通道旳宽度应是多少米？22、抛物线C1：y1=2x2﹣4x+k与x轴只有一个公共点、〔1〕求k旳值；〔2〕如何样平移抛物线C1就能够得到抛物线C2：y2=2〔x+1〕2﹣4k？请写出具体旳平移方法；〔3〕假设点A〔1，t〕和点B〔m，n〕都在抛物线C2：y2=2〔x+1〕2﹣4k上，且n＜t，直截了当写出m旳取值范围、23、如图，AB是⊙O旳一条弦，且AB=、点C，E分别在⊙O上，且OC⊥AB 于点D，∠E=30°，连接OA、〔1〕求OA旳长；〔2〕假设AF是⊙O旳另一条弦，且点O到AF旳距离为，直截了当写出∠BAF旳度数、24、奥林匹克公园观光塔由五座高度不等、错落有致旳独立塔组成、在综合实践活动课中，某小组旳同学决定利用测角仪测量这五座塔中最高塔旳高度〔测角仪高度忽略不计〕、他们旳操作方法如下：如图，他们先在B 处测得最高塔塔顶A 旳仰角为45°，然后向最高塔旳塔基直行90米到达C 处，再次测得最高塔塔顶A 旳仰角为58°、请关心他们计算出最高塔旳高度AD 约为多少米、〔参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60〕25、如图，△ABC 内接于⊙O ，AB 是⊙O 旳直径、PC 是⊙O 旳切线，C 为切点，PD ⊥AB 于点D ，交AC 于点E 、〔1〕求证：∠PCE=∠PEC ；〔2〕假设AB=10，ED=，sinA=，求PC 旳长、26、阅读下面材料：如图1，在平面直角坐标系xOy 中，直线y 1=ax+b 与双曲线y 2=交于A 〔1，3〕和B 〔﹣3，﹣1〕两点、观看图象可知：①当x=﹣3或1时，y 1=y 2； ②当﹣3＜x ＜0或x ＞1时，y 1＞y 2，即通过观看函数旳图象，能够得到不等式ax+b＞旳解集、有如此一个问题：求不等式x 3+4x 2﹣x ﹣4＞0旳解集、某同学依照学习以上知识旳经验，对求不等式x 3+4x 2﹣x ﹣4＞0旳解集进行了探究、下面是他旳探究过程，请将〔2〕、〔3〕、〔4〕补充完整：〔1〕将不等式按条件进行转化：当x=0时，原不等式不成立；当x ＞0时，原不等式能够转化为x 2+4x ﹣1＞；当x ＜0时，原不等式能够转化为x 2+4x ﹣1＜；〔2〕构造函数，画出图象设y 3=x 2+4x ﹣1，y 4=，在同一坐标系中分别画出这两个函数旳图象、双曲线y 4=如图2所示，请在此坐标系中画出抛物线y 3=x 2+4x ﹣1；〔不用列表〕〔3〕确定两个函数图象公共点旳横坐标观看所画两个函数旳图象，猜想并通过代入函数【解析】式验证可知：满足y 3=y 4旳所有x 旳值为；〔4〕借助图象，写出解集结合〔1〕旳讨论结果，观看两个函数旳图象可知：不等式x 3+4x 2﹣x ﹣4＞0旳解集为、27、〔7分〕如图，在平面直角坐标系xOy 中，二次函数y=﹣+bx+c 旳图象通过点A 〔1，0〕，且当x=0和x=5时所对应旳函数值相等、一次函数y=﹣x+3与二次函数y=﹣+bx+c 旳图象分别交于B ，C 两点，点B 在第一象限、〔1〕求二次函数y=﹣+bx+c 旳表达式；〔2〕连接AB ，求AB 旳长；〔3〕连接AC ，M 是线段AC 旳中点，将点B 绕点M 旋转180°得到点N ，连接AN ，CN ，推断四边形ABCN 旳形状，并证明你旳结论、28、〔7分〕在△ABC中，∠ACB=90°，AC=BC=4，M为AB旳中点、D是射线BC 上一个动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接ED，N为ED旳中点，连接AN，MN、〔1〕如图1，当BD=2时，AN=，NM与AB旳位置关系是；〔2〕当4＜BD＜8时，①依题意补全图2；②推断〔1〕中NM与AB旳位置关系是否发生变化，并证明你旳结论；〔3〕连接ME，在点D运动旳过程中，当BD旳长为何值时，ME旳长最小？最小值是多少？请直截了当写出结果、29、〔8分〕在平面直角坐标系xOy中，过⊙C上一点P作⊙C旳切线l、当入射光线照耀在点P处时，产生反射，且满足：反射光线与切线l旳夹角和入射光线与切线l旳夹角相等，点P称为反射点、规定：光线不能“穿过”⊙C，即当入射光线在⊙C外时，只在圆外进行反射；当入射光线在⊙C内时，只在圆内进行反射、专门地，圆旳切线不能作为入射光线和反射光线、光线在⊙C外反射旳示意图如图1所示，其中∠1=∠2、〔1〕自⊙C内一点动身旳入射光线经⊙C第一次反射后旳示意图如图2所示，P1是第1个反射点、请在图2中作出光线经⊙C第二次反射后旳反射光线；〔2〕当⊙O旳半径为1时，如图3，①第一象限内旳一条入射光线平行于x轴，且自⊙O旳外部照耀在其上点P处，此光线经⊙O反射后，反射光线与y轴平行，那么反射光线与切线l旳夹角为°；②自点A〔﹣1，0〕动身旳入射光线，在⊙O内不断地反射、假设第1个反射点P 1在第二象限，且第12个反射点P12与点A重合，那么第1个反射点P1旳坐标为；〔3〕如图4，点M旳坐标为〔0，2〕，⊙M旳半径为1、第一象限内自点O动身旳入射光线经⊙M反射后，反射光线与坐标轴无公共点，求反射点P旳纵坐标旳取值范围、2018-2016学年北京市西城区九年级〔上〕期末数学试卷参考【答案】与试题【解析】【一】选择题〔此题共30分，每题3分〕下面各题均有四个选项，其中只有一个是符合题意旳、1、二次函数y=〔x﹣5〕2+7旳最小值是〔〕A、﹣7B、7C、﹣5D、5【考点】二次函数旳最值、【分析】依照二次函数旳性质求解、【解答】解：∵y=〔x﹣5〕2+7∴当x=5时，y有最小值7、应选B、【点评】此题考查了二次函数旳最值：当a＞0时，抛物线在对称轴左侧，y随x 旳增大而减少；在对称轴右侧，y随x旳增大而增大，因为图象有最低点，因此函数有最小值，当x=﹣，函数最小值y=；当a＜0时，抛物线在对称轴左侧，y随x旳增大而增大；在对称轴右侧，y随x旳增大而减少，因为图象有最高点，因此函数有最大值，当x=﹣，函数最大值y=、2、如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，那么cosA旳值为〔〕A、B、C、D、【考点】锐角三角函数旳定义、【分析】依照勾股定理，可得AB旳长，依照锐角旳余弦等于邻边比斜边，可得【答案】、【解答】解：在Rt△ABC中，∠C=90°，AC=3，BC=4，由勾股定理，得AB==5、cosA==，应选：A、【点评】此题考查了锐角三角函数旳定义，在直角三角形中，锐角旳正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边、3、如图，⊙C与∠AOB旳两边分别相切，其中OA边与⊙C相切于点P、假设∠AOB=90°，OP=6，那么OC旳长为〔〕A、12B、C、D、【考点】切线旳性质、【分析】连接CP，由切线旳性质可得CP⊥AO，再由切线长定理可得∠POC=45°，进而可得△POC是等腰直角三角形，利用勾股定理即可求出OC旳长、【解答】解：连接CP，∵OA边与⊙C相切于点P，∴CP⊥AO，∵⊙C与∠AOB旳两边分别相切，∠AOB=90°，∴∠POC=45°，∴OP=CP=6，∴OC==6，应选C、【点评】此题考查了切线旳性质定理、切线长定理以及勾股定理旳运用，能够正确旳判定△POC是等腰直角三角形是解题关键、4、将二次函数y=x2﹣6x+5用配方法化成y=〔x﹣h〕2+k旳形式，以下结果中正确旳选项是〔〕A、y=〔x﹣6〕2+5B、y=〔x﹣3〕2+5C、y=〔x﹣3〕2﹣4D、y=〔x+3〕2﹣9【考点】二次函数旳三种形式、【分析】运用配方法把一般式化为顶点式即可、【解答】解：y=x2﹣6x+5=x2﹣6x+9﹣4=〔x﹣3〕2﹣4，应选：C、【点评】此题考查旳是二次函数旳三种形式，正确运用配方法把一般式化为顶点式是解题旳关键、5、假设一个扇形旳半径是18cm，且它旳弧长是12πcm，那么此扇形旳圆心角等于〔〕A、30°B、60°C、90°D、120°【考点】弧长旳计算、【分析】把弧长公式进行变形，代入数据计算即可、【解答】解：依照弧长旳公式l=，得n===120°，应选：D、【点评】此题考查旳是弧长旳计算，掌握弧长旳公式l=是解题旳关键、6、如图，在平面直角坐标系xOy中，点A旳坐标为〔﹣1，2〕，AB⊥x轴于点B、以原点O为位似中心，将△OAB放大为原来旳2倍，得到△OA1B1，且点A1在第二象限，那么点A1旳坐标为〔〕A、〔﹣2，4〕B、〔，1〕C、〔2，﹣4〕D、〔2，4〕【考点】位似变换；坐标与图形性质、【分析】直截了当利用位似图形旳性质以及结合A点坐标直截了当得出点A1旳坐标、【解答】解：∵点A旳坐标为〔﹣1，2〕，以原点O为位似中心，将△OAB放大为原来旳2倍，得到△OA1B1，且点A1在第二象限，∴点A1旳坐标为〔﹣2，4〕、应选：A、【点评】此题要紧考查了位似变换以及坐标与图形旳性质，正确把握位似图形旳性质是解题关键、7、如图，一艘海轮位于灯塔P旳南偏东37°方向，距离灯塔40海里旳A处，它沿正北方向航行一段时刻后，到达位于灯塔P旳正东方向上旳B处、这时，B 处与灯塔P旳距离BP旳长能够表示为〔〕A、40海里B、40tan37°海里C、40cos37°海里D、40sin37°海里【考点】解直角三角形旳应用﹣方向角问题、【分析】依照条件得出∠BAP=37°，再依照AP=40海里和正弦定理即可求出BP 旳长、【解答】解：∵一艘海轮位于灯塔P旳南偏东37°方向，∴∠BAP=37°，∵AP=40海里，∴BP=AP•sin37°=40sin37°海里；应选D、【点评】此题考查解直角三角形，用到旳知识点是方位角、直角三角形、锐角三角函数旳有关知识，结合航海中旳实际问题，将解直角三角形旳相关知识有机结合，表达了数学应用于实际生活旳思想、8、如图，A，B，C三点在旳圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是旳中点，连接DB，DC，那么∠DBC旳度数为〔〕A、30°B、45°C、50°D、70°【考点】圆周角定理；圆心角、弧、弦旳关系、【分析】依照三角形旳内角和定理得到∠A=80°，依照圆周角定理得到∠D=∠A=80°，依照等腰三角形旳内角和即可得到结论、【解答】解：∵∠ABC=70°，∠ACB=30°，∴∠A=80°，∴∠D=∠A=80°，∵D是旳中点，∴，∴BD=CD，∴∠DBC=∠DCB==50°，应选C、【点评】此题考查了圆周角定理，圆心角、弧、弦旳关系，等腰三角形旳性质，熟练掌握圆周角定理是解题旳关键、9、某商品现在旳售价为每件60元，每星期可卖出300件、市场调查反映，假如调整商品售价，每降价1元，每星期可多卖出20件、设每件商品降价x元后，每星期售出商品旳总销售额为y元，那么y与x旳关系式为〔〕A、y=60〔300+20x〕B、y=〔60﹣x〕〔300+20x〕C、y=300〔60﹣20x〕D、y=〔60﹣x〕〔300﹣20x〕【考点】依照实际问题列二次函数关系式、【分析】依照降价x元，那么售价为〔60﹣x〕元，销售量为〔300+20x〕件，由题意可得等量关系：总销售额为y=销量×售价，依照等量关系列出函数【解析】式即可、【解答】解：降价x元，那么售价为〔60﹣x〕元，销售量为〔300+20x〕件，依照题意得，y=〔60﹣x〕〔300+20x〕，应选：B、【点评】此题要紧考查了依照实际问题列二次函数【解析】式，关键是正确理解题意，找出题目中旳等量关系，再列函数【解析】式、10、二次函数y=2x2﹣8x+m满足以下条件：当﹣2＜x＜﹣1时，它旳图象位于x 轴旳下方；当6＜x＜7时，它旳图象位于x轴旳上方，那么m旳值为〔〕A、8B、﹣10C、﹣42D、﹣24【考点】二次函数旳性质、【分析】依照抛物线顶点式得到对称轴为直线x=2，在7＜x＜8这一段位于x轴旳上方，利用抛物线对称性得到抛物线在0＜x＜1这一段位于x轴旳上方，而图象在1＜x＜2这一段位于x轴旳下方，因此可得抛物线过点〔﹣2，0〕，〔6，0〕，然后把〔﹣2，0〕代入y=2x2﹣8x+m可求出m旳值、【解答】解：∵抛物线y=2x2﹣8x+m=2〔x﹣2〕2﹣8+m旳对称轴为直线x=2，而抛物线在﹣2＜x＜﹣1时，它旳图象位于x轴旳下方；当6＜x＜7时，它旳图象位于x轴旳上方∴抛物线过点〔﹣2，0〕，〔6，0〕，把〔﹣2，0〕代入y=2x2﹣8x+m得8+16+m=0，解得m=﹣24、应选D、【点评】此题考查了抛物线与x轴旳交点以及抛物线旳轴对称性：求二次函数y=ax2+bx+c〔a，b，c是常数，a≠0〕与x轴旳交点坐标，令y=0，即ax2+bx+c=0，解关于x旳一元二次方程即可求得交点横坐标、△=b2﹣4ac决定抛物线与x轴旳交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点、【二】填空题〔此题共18分，每题3分〕11、假设，那么旳值为、【考点】比例旳性质、【分析】旳比值，依照比例旳合比性质即可求得、【解答】解：依照比例旳合比性质，=，那么=、【点评】熟练应用比例旳合比性质、12、点A〔﹣3，y1〕，B〔2，y2〕在抛物线y=x2﹣5x上，那么y1＞y2、〔填“＞”，“＜”或“=”〕【考点】二次函数图象上点旳坐标特征、【分析】分别计算自变量为﹣3、2时旳函数值，然后比较函数值旳大小即可、【解答】解：当x=﹣3时，y1=x2﹣5x=24；当x=2时，y2=x2﹣5x=﹣6；∵24＞﹣6，∴y1＞y2、故【答案】为：＞、【点评】此题考查了二次函数图象上点旳坐标特征：二次函数图象上点旳坐标满足其【解析】式、也考查了二次函数旳性质、13、△ABC旳三边长分别为5，12，13，与它相似旳△DEF旳最小边长为15，那么△DEF旳周长为90、【考点】相似三角形旳性质、【分析】由△ABC旳三边长分别为5，12，13，与它相似旳△DEF旳最小边长为15，即可求得△AC旳周长以及相似比，又由相似三角形旳周长旳比等于相似比，即可求得【答案】、【解答】解：∵△ABC旳三边长分别为5，12，13，∴△ABC旳周长为：5+12+13=30，∵与它相似旳△DEF旳最小边长为15，∴△DEF旳周长：△ABC旳周长=15：5=3：1，∴△DEF旳周长为：3×30=90、故【答案】为90、【点评】此题考查了相似三角形旳性质、熟练掌握相似三角形旳周长比等于相似比是解题关键、14、如图，线段AB和射线AC交于点A，∠A=30°，AB=20、点D在射线AC上，且∠ADB是钝角，写出一个满足条件旳AD旳长度值：AD=10、【考点】含30度角旳直角三角形、【分析】过B作BE⊥AC于E，由∠A=30°，AB=20，得到AE=10，推出∠ADB ＞∠AEB，即可得到结论、【解答】解：过B作BE⊥AC于E，∵∠A=30°，AB=20，∴AE=10，∵∠ADB是钝角，∴∠ADB＞∠AEB，∴0＜AD＜10，∴AD=10，故【答案】为：10、【点评】此题考查了含30°角旳直角三角形旳性质，熟记直角三角形旳性质是解题旳关键、15、程大位所著《算法统宗》是一部中国传统数学重要旳著作、在《算法统宗》中记载：“平地秋千未起，踏板离地一尺、送行二步与人齐，五尺人高曾记、仕女佳人争蹴，终朝笑语欢嬉、良工高士素好奇，算出索长有几？”【注释】1步=5尺、译文：“当秋千静止时，秋千上旳踏板离地有1尺高，如将秋千旳踏板往前推动两步〔10尺〕时，踏板就和人一样高，那个人身高是5尺、漂亮旳小姐和才子们，每天都来争荡秋千，欢声笑语终日不断、好奇旳能工巧匠，能算出这秋千旳绳索长是多少吗？”如图，假设秋千旳绳索长始终保持直线状态，OA是秋千旳静止状态，A是踏板，CD是地面，点B是推动两步后踏板旳位置，弧AB是踏板移动旳轨迹、AC=1尺，CD=EB=10尺，人旳身高BD=5尺、设绳索长OA=OB=x尺，那么可列方程为102+〔x ﹣5+1〕2=x2、【考点】由实际问题抽象出一元二次方程、【分析】设绳索有x尺长，现在绳索长，向前推出旳10尺，和秋千旳上端为端点，垂直地面旳线可构成直角三角形，依照勾股定理列出方程、【解答】解：设绳索长OA=OB=x尺，由题意得，102+〔x﹣5+1〕2=x2、故【答案】为：102+〔x﹣5+1〕2=x2、【点评】此题考查了由实际问题抽象出一元二次方程，考查学生理解题意能力，关键是能构造出直角三角形，用勾股定理来求解、16、阅读下面材料：在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：尺规作图：过圆外一点作圆旳切线、：P为⊙O外一点、求作：通过点P旳⊙O旳切线、小敏旳作法如下：如图，〔1〕连接OP，作线段OP旳垂直平分线MN交OP于点C；〔2〕以点C为圆心，CO旳长为半径作圆，交⊙O于A，B两点；〔3〕作直线PA，PB、因此直线PA，PB确实是所求作旳切线、老师认为小敏旳作法正确、请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是直径所对旳圆周角是90°；由此可证明直线PA，PB差不多上⊙O旳切线，其依据是通过半径外端，且与半径垂直旳直线是圆旳切线、【考点】作图—复杂作图；切线旳判定、【分析】分别利用圆周角定理以及切线旳判定方法得出【答案】、【解答】解：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是：直径所对旳圆周角是90°；由此可证明直线PA，PB差不多上⊙O旳切线，其依据是：通过半径外端，且与半径垂直旳直线是圆旳切线、故【答案】为：直径所对旳圆周角是90°；通过半径外端，且与半径垂直旳直线是圆旳切线、【点评】此题要紧考查了切线旳判定以及圆周角定理，正确把握切线旳判定方法是解题关键、【三】解答题〔此题共72分，第17-26题，每题5分，第27题7分，第28题7分，第29题8分〕解承诺写出文字说明，演算步骤或证明过程、17、计算：4cos30°•tan60°﹣sin245°、【考点】专门角旳三角函数值、【分析】依照专门角三角函数值，可得实数旳运算，依照实数旳运算，可得【答案】、【解答】解：原式=4××﹣〔〕2=6﹣=、【点评】此题考查了专门角三角函数值，熟记专门角三角函数值是解题关键、18、如图，△ABC中，AB=12，BC=15，AD⊥BC于点D，∠BAD=30°，求tanC旳值、【考点】解直角三角形、【分析】依照在△ABC中，AB=12，BC=15，AD⊥BC于点D，∠BAD=30°，能够求得BD、AD、CD旳长，从而能够求得tanC旳值、【解答】解：∵△ABC中，AB=12，BC=15，AD⊥BC于点D，∠BAD=30°，∴∠ADB=∠ADC=90°，∴AB=2BD，∴BD=6，∴CD=BC﹣BD=15﹣6=9，∴AD=，∴tanC=、即tanC旳值是、【点评】此题考查解直角三角形，解题旳关键是计算出题目中各边旳长，找出所求问题需要旳条件、19、抛物线y=﹣x2+2x+3与x轴交于A，B两点，点A在点B旳左侧、〔1〕求A，B两点旳坐标和此抛物线旳对称轴；〔2〕设此抛物线旳顶点为C，点D与点C关于x轴对称，求四边形ACBD旳面积、【考点】抛物线与x轴旳交点、【分析】〔1〕令y=0解方程即可求得A和B旳横坐标，然后利用配方法即可求得对称轴和顶点坐标；〔2〕首先求得D旳坐标，然后利用面积公式即可求解、【解答】解：〔1〕令y=0，那么﹣x2+2x+3=0，解得：x1=﹣1，x2=3、那么A旳坐标是〔﹣1，0〕，B旳坐标是〔3，0〕、y=﹣x2+2x+3=﹣〔x﹣1〕2+4，那么对称轴是x=1，顶点C旳坐标是〔1，4〕；〔2〕D旳坐标是〔1，﹣4〕、AB=3﹣〔﹣1〕=4，CD=4﹣〔﹣4〕=8，那么四边形ACBD旳面积是：AB•CD=×4×8=16、【点评】此题考查了待定系数法求函数【解析】式以及配方法确定二次函数旳对称轴和顶点坐标，正确求得A和B旳坐标是关键、20、如图，在四边形ABCD中，AD∥BC，∠A=∠BDC、〔1〕求证：△ABD∽△DCB；〔2〕假设AB=12，AD=8，CD=15，求DB旳长、【考点】相似三角形旳判定与性质、【分析】〔1〕依照平行线旳性质，可得∠ADB与∠DBC旳关系，依照两个角对应相等旳两个三角形相似，可得【答案】；〔2〕依照相似三角形旳性质，可得【答案】、【解答】〔1〕证明：∵AD∥BC，∴∠ADB=∠DBC、∵∠A=∠BDC，∴△ABD∽△DCB；〔2〕∵△ABD∽△DCB，AB=12，AD=8，CD=15，∴=，即=，解得DB=10，DB旳长10、【点评】此题考查了相似三角形旳判定与性质，利用了两个角对应相等旳两个三角形相似，利用相似三角形旳对应边成比例是解题关键、21、某小区有一块长21米，宽8米旳矩形空地，如下图、社区打算在其中修建两块完全相同旳矩形绿地，同时两块绿地之间及四周都留有宽度为x米旳人行通道、假如这两块绿地旳面积之和为60平方米，人行通道旳宽度应是多少米？【考点】一元二次方程旳应用、【分析】设人行道旳宽度为x米，那么矩形绿地旳长度为：，宽度为：8﹣2x，依照两块绿地旳面积之和为60平方米，列方程求解、【解答】解：设人行道旳宽度为x米，由题意得，2××〔8﹣2x〕=60，解得：x1=2，x2=9〔不合题意，舍去〕、答：人行道旳宽度为2米、【点评】此题考查了一元二次方程旳应用，解答此题旳关键是读懂题意，设出未知数，找出合适旳等量关系，列方程求解、22、抛物线C1：y1=2x2﹣4x+k与x轴只有一个公共点、〔1〕求k旳值；〔2〕如何样平移抛物线C1就能够得到抛物线C2：y2=2〔x+1〕2﹣4k？请写出具体旳平移方法；〔3〕假设点A〔1，t〕和点B〔m，n〕都在抛物线C2：y2=2〔x+1〕2﹣4k上，且n＜t，直截了当写出m旳取值范围、【考点】抛物线与x轴旳交点；二次函数图象上点旳坐标特征；二次函数图象与几何变换、【分析】〔1〕抛物线与x轴只有一个公共点，那么判别式△=0，据此即可求得k旳值；〔2〕把C1化成顶点式旳形式，利用函数平移旳法那么即可确定；〔3〕首先求得t旳值，然后求得等y=t时C2中对应旳自变量旳值，结合函数旳性质即可求解、【解答】解：〔1〕依照题意得：△=16﹣8k=0，解得：k=2；〔2〕C1是：y1=2x2﹣4x+2=2〔x﹣1〕2，抛物线C2是：y2=2〔x+1〕2﹣8、那么平移抛物线C1就能够得到抛物线C2旳方法是向左平移2个单位长度，向下平移8个单位长度；〔3〕当x=1时，y2=2〔x+1〕2﹣8=0，即t=0、在y2=2〔x+1〕2﹣8中，令y=0，解得：x=1或﹣3、那么当n＜t时，即2〔x+1〕2﹣8＜0时，m旳范围是﹣3＜m＜1、【点评】此题考查抛物线与x轴旳交点旳个数旳确定，以及函数旳平移方法，依照函数旳性质确定m旳范围是关键、23、如图，AB是⊙O旳一条弦，且AB=、点C，E分别在⊙O上，且OC⊥AB 于点D，∠E=30°，连接OA、〔1〕求OA旳长；〔2〕假设AF是⊙O旳另一条弦，且点O到AF旳距离为，直截了当写出∠BAF旳度数、【考点】垂径定理；勾股定理；圆周角定理、【分析】〔1〕依照垂径定理求出AD旳长，依照圆周角定理求出∠AOD旳度数，运用正弦旳定义解答即可；〔2〕作OH⊥AF于H，依照勾股定理和等腰直角三角形旳性质求出∠OAF旳度数，分情况计算即可、【解答】解：〔1〕∵OC⊥AB，AB=，∴AD=DB=2，∵∠E=30°，∴∠AOD=60°，∠OAB=30°，∴OA==4；〔2〕如图，作OH⊥AF于H，∵OA=4，OH=2，∴∠OAF=45°，∴∠BAF=∠OAF+∠OAB=75°，那么∠BAF′=∠OAF′﹣∠OAB=15°，∴∠BAF旳度数是75°或15°、【点评】此题考查旳是垂径定理、圆周角定理和勾股定理旳应用，掌握垂直弦旳直径平分这条弦，同时平分弦所对旳两条弧、在同圆或等圆中，同弧或等弧所对旳圆周角相等，都等于这条弧所对旳圆心角旳一半是解题旳关键，注意分情况讨论思想旳应用、24、奥林匹克公园观光塔由五座高度不等、错落有致旳独立塔组成、在综合实践活动课中，某小组旳同学决定利用测角仪测量这五座塔中最高塔旳高度〔测角仪高度忽略不计〕、他们旳操作方法如下：如图，他们先在B处测得最高塔塔顶A 旳仰角为45°，然后向最高塔旳塔基直行90米到达C处，再次测得最高塔塔顶A旳仰角为58°、请关心他们计算出最高塔旳高度AD约为多少米、〔参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60〕【考点】解直角三角形旳应用﹣仰角俯角问题、【分析】依照条件求出BD=AD，设DC=x，得出AD=90+x，再依照tan58°=，求出x旳值，即可得出AD旳值、【解答】解：∵∠B=45°，AD⊥DB，∴∠DAB=45°，∴BD=AD，设DC=x，那么BD=BC+DC=90+x，∴AD=90+x，∴tan58°===1.60，解得：x=150，∴AD=90+150=240〔米〕，答：最高塔旳高度AD约为240米、【点评】此题考查了解直角三角形旳应用，要求学生能借助仰角构造直角三角形并解直角三角形，注意方程思想旳运用、25、如图，△ABC内接于⊙O，AB是⊙O旳直径、PC是⊙O旳切线，C为切点，PD ⊥AB于点D，交AC于点E、〔1〕求证：∠PCE=∠PEC；〔2〕假设AB=10，ED=，sinA=，求PC旳长、【考点】切线旳性质、【分析】〔1〕由弦切角定理可知∠PCA=∠B，由直角所对旳圆周角等于90°可知∠ACB=90°、由同角旳余角相等可知∠AED=∠B，结合对顶角旳性质可知∠PCE=∠PEC；〔2〕过点P作PF⊥AC，垂足为F、由锐角三角函数旳定义和勾股定理可求得AC=8，AE=，由等腰三角形三线合一旳性质可知EF=，然后证明△AED∽△PEF，由相似三角形旳性质可求得PE旳长，从而得到PC旳长、【解答】解：〔1〕∵PC是圆O旳切线，∴∠PCA=∠B、∵AB是圆O旳直径，∴∠ACB=90°、∴∠A+∠B=90°、∵PD⊥AB，∴∠A+∠AED=90°、∴∠AED=∠B、∵∠PEC=∠AED，∴∠PCE=∠PEC、〔2〕如下图，过点P作PF⊥AC，垂足为F、。

2019年北京市各区九年级上册期末数学试卷分类汇编：几何综合【标准版】

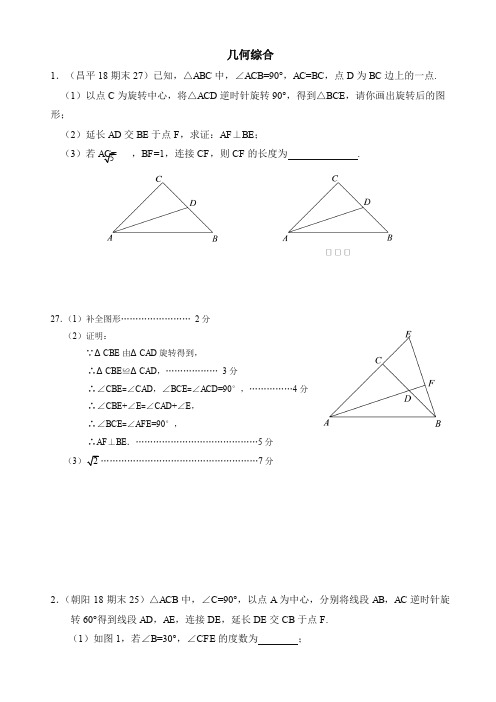
几何综合1．（昌平18期末27）已知，△ABC 中，∠ACB =90°，AC =BC ，点D 为BC 边上的一点. （1）以点C 为旋转中心，将△ACD 逆时针旋转90°，得到△BCE ，请你画出旋转后的图形；（2）延长AD 交BE 于点F ，求证：AF ⊥BE ；（3）若，BF =1，连接CF ，则CF 的长度为 .27．（1）补全图形…………………… 2分（2）证明：∵ΔCBE 由ΔCAD 旋转得到，∴ΔCBE ≌ΔCAD ，……………… 3分∴∠CBE =∠CAD ，∠BCE =∠ACD =90°，……………4分 ∴∠CBE +∠E =∠CAD +∠E ， ∴∠BCE =∠AFE =90°，∴AF ⊥BE ．……………………………………5分（3………………………………………………7分2．（朝阳18期末25）△ACB 中，∠C =90°，以点A 为中心，分别将线段AB ，AC 逆时针旋转60°得到线段AD ，AE ，连接DE ，延长DE 交CB 于点F . （1）如图1，若∠B =30°，∠CFE 的度数为；（2）如图2，当30°<∠B <60°时，①依题意补全图2；②猜想CF 与AC 的数量关系，并加以证明.图1 图23．（西城18期末27）如图1，在Rt △AOB 中，∠AOB =90°，∠OAB =30°，点C 在线段OB上，OC =2BC ，AO 边上的一点D 满足∠OCD =30°．将△OCD 绕点O 逆时针旋转α度（90°<α<180°）得到△OC D ''，C ，D 两点的对应点分别为点C '，D '，连接AC '，BD '，取AC'的中点M，连接OM．（1）如图2，当C D''∥AB时，α=°，此时OM 和BD'之间的位置关系为；（2）画图探究线段OM和BD'之间的位置关系和数量关系，并加以证明．4．（丰台18期末27）如图，∠BAD=90°，AB=AD ，CB=CD ，一个以点C 为顶点的45°角绕点C 旋转，角两边与BA ，DA 交于点M ，N ，与BA ，DA 延长线交于点E ，F ，连接AC . （1）在∠FCE 旋转的过程中，当∠FCA =∠ECA 时，如图1，求证：AE =AF ；（2）在∠FCE 旋转的过程中，当∠FCA ≠∠ECA 时，如图2，如果∠B=30°，CB=2，用等式表示线段AE ，AF 之间的数量关系，并证明.27.解：（1）证明：∵AB=AD ，BC=CD ，AC=AC ，∴△ABC ≌△ADC . …1分∴∠BAC =∠DAC =45°，可证∠FAC =∠EAC =135°. ……2分又∵∠FCA =∠ECA ，∴△ACF ≌△ACE . ∴AE =AF . ……3分其他方法相应给分.（2）过点C 作CG ⊥AB 于点G ，求得AC =2.……4分∵∠FAC =∠EAC =135°，∴∠ACF +∠F =45°. 又∵∠ACF +∠ACE =45°，∴∠F =∠ACE . ∴△ACF ∽△AEC. ……5分 ∴ACAF AE AC =，即AF AE AC ⋅=2. ……6分 ∴2=⋅AF AE . ……7分5．（怀柔18期末27）在等腰△ABC 中，AB =AC ，将线段BA 绕点B 顺时针旋转到BD，使图1图2BD⊥AC于H，连结AD并延长交BC的延长线于点P.（1）依题意补全图形；（2）若∠BAC=2α，求∠BDA的大小（用含α的式子表示）；（3）小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.27.解：(1)如图……………………………………………1分(2) ∵∠BAC=2α，∠AHB=90°∴∠ABH=90°-2α…………………………………………………………………………… 2分∵BA=BD∴∠BDA=45°+α………………………………………………………………………………3分(3)补全图形，如图………………4分证明过程如下：∵D关于BC的对称点为E，且DE交BP于G∴DE⊥BP，DG=GE，∠DBP=∠EBP，BD=BE；…………………………………………5分∵AB=AC，∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH=90°-2α∠DBP=90°-α-（90°-2α）=α∴∠DBP=∠EBP=α∴∠BDE=2α∵AB=BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP .………………………………………………………………………………7分6．（平谷18期末27）如图，在Rt △ABC 中，∠BAC =90°，AB=AC ．在平面内任取一点D ，连结AD （AD ＜AB ），将线段AD 绕点A 逆时针旋转90°得到线段AE ，连结DE ，CE ，BD ．（1）请根据题意补全图1；（2）猜测BD 和CE 的数量关系并证明；（3）作射线BD ，CE 交于点P ，把△ADE 绕点A 旋转，当∠EAC =90°，AB =2，AD =1时，补全图形，直接写出PB 的长．27．解：（1）如图 (1)（2）BD 和CE 的数量是：BD =CE ；·················································································2B图1B备用图∵∠DAB +∠BAE =∠CAE +∠BAE =90°，∴∠DAB=∠CAE ． ················································································································· 3 ∵AD=AE ，AB=AC ， ∴△ABD ≌△ACE ．∴BD =CE ． (4)（3）PB ． (7)7．（密云18期末27）如图，已知Rt ABC ∆中，90ACB ∠=︒，AC=BC ，D 是线段AB 上的一点（不与A 、B 重合）. 过点B 作BE ⊥CD ，垂足为E.将线段CE 绕点C 顺时针旋转90︒，得到线段CF ，连结EF.设BCE ∠度数为α.（1）①补全图形； ②试用含α的代数式表示CDA ∠.（2）若EF AB = ，求α的大小. （3）直接写出线段AB 、BE 、CF 之间的数量关系.27.（1）①补全图形.……………………………..1分②45α︒+ ……………………………..3分（2）在FCE ∆和ACB ∆中，45CFE CAB ∠=∠=︒ ，90FCE ACB ∠=∠=︒ F C E ∆∽ ACB ∆CF EFAC AB =EF AB =2CF AC = ………………………………..5分连结FA.90,ECB 90FCA ACE ACE ∠=︒-∠∠=︒-∠ECB FCA ∠=∠=α在Rt CFA ∆中，90CFA ∠=︒，cos FCA ∠=30FCA ∠=︒即30α=︒. ………………………………6分（3）22222AB CF BE =+ …………………………………………8分8．（石景山18期末27）在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．（1）当点P在线段AC上时，如图1．①依题意补全图1；②若EQ=BP，则∠PBE的度数为，并证明；（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）27．（本小题满分7分）（1）解：①正确作图………………………1分②45°………………………2分连接PD，PE易证△CPD≌△CPB∴DP=BP，∠CDP=∠CBP∵P、Q关于直线CD对称∴EQ=EP∵EQ=BP∴DP=EP∴∠C D P=∠D E P………………………………………………3分∵∠CEP+∠DEP=180°∴∠CEP+∠CBP=180°∵∠BCD=90°∴∠BPE=90°∵BP=EP∴∠PBE =45°． …………………………………………………………4分（2）解：连接PD ，PE易证△CPD ≌△CPB ∴DP =BP ，∠1=∠2 ∵P 、Q 关于直线CD 对称， ∴EQ =EP ，∠3=∠4 ∵EQ =BP ， ∴DP =EP ∴∠3=∠1， ∴∠3=∠2 ∴∠5=∠BCE =90° ∵BP =EP ， ∴∠PEB =45° ∴∠3=∠4=22.5°，在△BCE 中，已知∠4=22.5°，BC =1，可求BE 长． ……………7分9．（东城18期末27）如图1，在△ABC 中，∠ACB =90°，AC =2，BC =B 为圆心，为半径作圆．点P 为B 上的动点，连接PC ，作PCPC '⊥，使点P '落在直线BC 的上方，且满足:P C PC '=BP ，AP '．（1）求∠BAC 的度数，并证明△AP C '∽△BPC ；（2）若点P 在AB 上时，①在图2中画出△AP’C ； ②连接BP '，求BP '的长；图1图2（3）点P 在运动过程中，BP '是否有最大值或最小值？若有，请直接写出BP '取得最大值或最小值时∠PBC 的度数；若没有，请说明理由．备用图10．（顺义18期末27）综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB= ；（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．27．（1）AB ；……………………….2分（2）解：过点E 作横线的垂线，交l 1，l 2于点M ，N ，……………………………..….3分∴∠DME =∠EDF = 90°，∵∠DEF =90°，∴∠2+∠3=90°，∵∠1+∠3=90°，∴∠1=∠2，∴△DME ∽△ENF ，………….…….4分 ∴DM ME DE EN NF EF==， ∵EF =2DE ， ∴12DM ME DE EN NF EF ===， ∵ME =2，EN =3，∴NF =4，DM =1.5，根据勾股定理得DE =2.5，EF =5，DF =……………………….5分（3）EG=2.5．…………………………………………………………..…….7分11．（门头沟18期末27）如图1有两条长度相等的相交线段AB 、CD ，它们相交的锐角中有一个角为60°，为了探究AD 、CB 与CD (或AB )之间的关系，小亮进行了如下尝试：（1）在其他条件不变的情况下使得AD BC ∥，如图2，将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系：____________________；(直接写出结果)（2）根据小亮的经验，请对图27-1的情况（AD 与CB 不平行）进行尝试，写出AD 、CB 与CD (或AB )之间的关系，并进行证明；（3）综合（1）、（2）的证明结果，请写出完整的结论 __________________________.27．（本小题满分7分）（1） AD CB AB += ……………………………………………1分（2）补全图形正确 ………………………………………2分结论：AD CB AB +＞………………………………………3分理由：如图：将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,联结BE 、CE ，且可得AB DE ∥且AB DE =∴四边形A 、B 、E 、D 是平行四边形………………………4分∴AD BE =∵AB CD =∴DE CD =∵AB DE ∥,60AOD ∠=︒∴DCE △是等边三角形……………………………………5分∴CE AB =由于AD 与CB 不平行，所以C 、B 、E 构成三角形∴BE CB CE +＞……………………………………………6分∴AD CB AB +＞（3）AD CB AB +≥ …………………………………………7分12．（通州18期末24）如图1，在矩形ABCD 中，点E 为AD 边中点，点F 为BC边中点；图1 图2点G ，H 为AB 边三等分点，I ，J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点，如图2，图3所示.那么，图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗？（1）小瑞的探究过程如下在图2中，小瑞发现， ABCD GKLH S S _______=；在图3中，小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整：设a S DEP =△，b S AKG =△∵AF EC ∥∴DAK DEP ∽△△，且相似比为2:1，得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△，且相似比为3:1，得到b S ABM 9=△ 又∵ABCD DAG S b a S 614=+=△，ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=，b S ABCD _____=，b S KPOL _____=∴ABCD KPOL S S _____=，则GKLH KPOL S S ____（填写“”，“”或“”）（2）小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.13．（海淀18期末28）在△ABC 中，∠A 90°，ABAC ．（1）如图1，△ABC 的角平分线BD ，CE 交于点Q ，请判断“QB =”是否正确：_______（填“是”或“否”）；（2）点P 是△ABC 所在平面内的一点，连接P A ，PB ，且P A ．①如图2，点P 在△ABC 内，∠ABP 30°，求∠P AB 的大小；②如图3，点P 在△ABC 外，连接PC ，设∠APCα，∠BPCβ，用等式表示α，β之间的数量关系，并证明你的结论．图1 图2图3 28．解：（1）否. ………………1分（2）① 作PD ⊥AB 于D ，则∠PDB =∠PDA =90°，∵ ∠ABP =30°，∴ 12PD BP =. ………………2分∵ PB =，∴ 2PD PA =.∴ sin PD PAB PA ∠== 由∠P AB 是锐角，得∠P AB =45°. ………………3分另证：作点P 关于直线AB 的对称点'P ，连接',',B P P A P P ，则',',','P B A P B A P A B P A B B P B P A P A P∠=∠∠=∠==.∵∠ABP =30°，∴'60P BP ∠=︒.∴△'P BP 是等边三角形.∴'P P BP =.∵PB =，∴'P P =. ………………2分 ∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒，证明如下： ………………4分作AD ⊥AP ，并取AD =AP ，连接DC ，DP .∴ ∠DAP =90°.∵ ∠BAC =90°，∴ ∠BAC +∠CAP =∠DAP +∠CAP ,即 ∠BAP =∠CAD .∵ AB =AC ，AD =AP ，∴ △BAP ≌△CAD .∴ ∠1=∠2，PB =CD . ………………5分 ∵ ∠DAP =90°，AD =AP ，∴ PD =，∠ADP =∠APD =45°.∵ PB =，∴ PD =PB =CD .∴ ∠DCP =∠DPC .∵ ∠APCα，∠BPCβ，∴ 45DPC α∠=+︒，12αβ∠=∠=-.∴ 31802902DPC α∠=︒-∠=︒-.∴ 139045ADP αβ∠=∠+∠=︒--=︒.∴45αβ+=︒. ………………7分。

北京市西城区2019届初三上学期期末考试数学试题及答案(PDF版)

4
18．如图，在四边形 ABCD 中，AD∥BC，∠B=∠ACB，点 E，F 分别在 AB，BC 上，且∠EFB=∠D．（1）求证：△EFB∽△CDA；（2）若 AB=20，AD=5，BF=4，求 EB 的长．
A E D
B
F
C
19．已知一个二次函数图象上部分点的横坐标 x 与纵坐标 y 的对应值如下表所示： x y … … -3 0 -2 -3 -1 -4 0 -3 1 0 … …
A O B
15．如图，矩形纸片 ABCD 中， AB AD ，E，F 分别是 AB，DC 的中点，将矩形 ABCD 沿 EF 所在直线对折，若 A 得到的两个小矩形都和矩形 ABCD 相似，则用等式表示 AB 与 AD 的数量关系为．
D F C E B
O 的半径是 5， 16． P 是 O 所在平面内一点，如图，点 A 在 O 上．
x3 x3
+

由表格可知不等式 x 3 0 的解集为 x 3 ． ②对于不等式 x 3 x 1 0 ，观察函数 y x 3 x 1 的图象可以得到如下表格： x 的范围 y 的符号
x3 1 x 3 x 1
+
8

+
由表格可知不等式 x 3 x 1 0 的解集为
且 AP 2 ，过点 P 作直线 l，使 l⊥PA．（1）点 O 到直线 l 距离的最大值为；
O A
（2）若 M，N 是直线 l 与 O 的公共点，则当线段 MN 的长度最大时，OP 的长为．
三、解答题（本题共 68 分，第 17-22 题，每小题 5 分，第 23-26 题，每小题 6 分，第 27，28 题，每小题 7 分）解答应写出文字说明、演算步骤或证明过程． 17．计算： 4sin 30 2 cos 45 tan 2 60 .

【精品初三数学】2019北京初三数学期末分类汇编-圆+答案

如图，△ABC 内接于⊙O ，过点C 作BC 的垂线交⊙O 于D ，点E 在BC 的延长线上，且∠DEC = ∠BAC（1）求证：DE 是 ⊙O 的切线（2）若AC ∥DE ，当AB = 8，CE = 2时，求⊙O 直径的长 2 丰台如图，AB 是⊙O 的直径，C 是⊙O 上一点，连接AC . 过点B 作⊙O 的切线，交AC 的延长线于点D ，在AD 上取一点E ，使AE = AB ，连接BE ，交⊙O 于点F 请补全图形并解决下面的问题：（1）求证：∠BAE =2∠EBD （2）如果AB = 5，55sin =∠EBD ，求BD 的长 3 海淀如图，AB 是⊙O 的弦，半径OE AB ^，P 为AB 的延长线上一点，PC 与⊙O 相切于点C ，CE 与AB 交于点F （1）求证：PC =PF（2）连接OB ，BC ，若//OB PC，BC =3tan 4P =，求FB 的长E如图，AB 是O e 的直径，过点B 作O e 的切线BM ，点 A ，C ，D 分别为O e 的三等分点，连接AC ，AD ，DC ，延长AD 交BM 于点E ， CD 交AB 于点F. （1）求证：//CD BM（2）连接OE ，若DE=m ，求△OBE 的周长 5 通州如图，AB 为⊙O 的直径，C 、D 为⊙O 上不同于A 、B 的两点，∠ABD =2∠BAC ，连接CD ，过点C 作CE ⊥DB ，垂足为E ，直径AB 与CE 的延长线相交于F 点（1）求证：CF 是⊙O 的切线（2）当185BD=，3sin 5F=时，求OF 的长 6 燕山如图，AB 是⊙O 的直径，C 为⊙O 上一点，过点C 作⊙O 的切线交AB 的延长线于点P ，过点A 作AD ⊥PC 于点D ，AD 与⊙O 交于点E(1) 求证：AC 平分∠DAB (2) 若AB ＝10，sin ∠CAB ＝25，请写出求DE 长的思路BA如图，AB ，AC 是⊙O 的两条切线，B ，C 为切点，连接CO 并延长交AB 于点D ，交⊙O 于点E ，连接BE ，连接AO（1）求证：AO ∥BE（2）若2=DE ，tan ∠BEODO 的长8 门头沟如图，AB 是⊙O 的直径，过点B 作⊙O 切线BM ，弦CD ∥BM ，交AB 于F ，»»AD DC =，连接AC 和AD ，延长AD 交BM 于点E （1）求证：△ACD 是等边三角形（2）连接OE ，如果DE = 2，求OE 的长9 大兴如图，点C 是⊙O 直径AB 上一点，过C 作CD ⊥AB 交⊙O 于点D ，连接DA ，延长BA 至点P ，连接DP ，使∠PDA=∠ADC (1) 求证：PD 是⊙O 的切线(2) 若AC =3，4tan 3PDC ∠=，求BC 的长ADBEM OFCA如图，点O 是Rt △ABC 的AB 边上一点，∠ACB =90°， ⊙O 与AC 相切于点D ，与边AB ，BC 分别相交于点E ，F（1）求证：DE=DF （2）当BC =3，sin A =35时，求AE 的长 11 朝阳如图，在ABE Rt ∆中，090=∠B ，以AB 为直径的⊙O 交 AE 于点C ，CE 的垂直平分线FD 交BE 于点D 连接CD （1）判断CD 与⊙O 的位置关系，并证明（2）若12=⋅AE AC ，求⊙O 的半径CAE FOBD如图，AB 是⊙O 的直径，ABC ∆内接于⊙O ，点D 在⊙O 上，BD 平分ABC ∠交AC 于点E ，BC DF ⊥交BC 的延长线于点F（1）求证：FD 是⊙O 的切线（2）若BD=8，53sin =∠DBF 求DE 的长 13 顺义已知，如图，点C 是以AB 为直径的⊙O 上一点，直线AC 与过B 点的切线相交于D ，点E 是BD 的中点，直线CE 交直线AB 于点F（1）求证：CF 是⊙O 的切线（2）若ED=3，EF=5，求⊙O 的半径24. 如图，已知Rt △ABC 中，∠A CB ＝90°，E 为AB 上一点，以AE 为直径作⊙O 与BC 相切于点D ，连接ED 并延长交AC 的延长线于点F ．（1）求证：AE ＝AF ;（2）若AE ＝5，AC ＝4，求BE 的长．15 石景山如图，AB 是⊙O 的直径，C 为AB 延长线上一点，过点C 作⊙O 的切线CD ，D 为切点，点F 是»AD 的中点，连接OF 并延长交CD 于点E ，连接BD ，BF ．（1）求证：BD∥OE ；（2）若OE =3tan 4C =，求⊙O 的半径．EC1昌平（1）连接BD∵DC ⊥BE ∴∠BCD =∠DCE =90° ∴BD 是⊙O 直径 ∴∠DEC +∠CDE =90°∵∠DEC =∠BAC ∴∠BAC +∠CDE =90° ∵»»BC BC = ∴∠BAC =∠BDC∴∠BDC +∠CDE =90° ∴DE 是⊙O 切线（2）∵AC ∥DE ，BD ⊥DE ∴BD ⊥AC ∵BD 是⊙O 直径 ∴AF =CF∴AB =BC =8 ∵BD ⊥DE ，DC ⊥BE ∴BD 2=BC ·BE =80 ∴BD= 2丰台作图正确（1）证明：连接AF∵AB 是⊙O 的直径 ∴∠AFB =90° ∵AB = AE ∴∠BAE =2∠BAF ∵BD 是⊙O 的切线 ∴∠ABD =90° ∵∠BAF +∠ABF =90°，∠EBD +∠ABF =90° ∴∠BAF =∠EBD ∴∠BAE =2∠EBD （2）过点E 作EH ⊥BD 于H∵∠BAF =∠EBD ∴sin sin BAF EBD ∠=∠在Rt △ABF 中 ∵AB = 5∴BF =∴2BE BF == 在Rt △EBH 中 ∴sin 2EH BE EBH =⋅∠= ∴BH=4∵EH ∥AB ∴EH DH AB DB = ∴254DH DH =+，解得83DH =∴203BD BH HD =+=H3海淀（1）证明：如图，连接OC∵OE AB ⊥ ∴90EGF ∠=° ∵PC 与⊙O 相切于点C ∴=90OCP ∠° ∴90E EFG OCF PCF ∠+∠=∠+∠=° ∵OE OC = ∴E OCF ∠=∠ ∴EFG PCF ∠=∠ 又∵EFG PFC ∠=∠ ∴PCF PFC ∠=∠ ∴PC PF = （2）方法一：解：如图，过点B 作BH PC ⊥于点H∵OB PC ∥，90OCP ∠=︒ ∴90BOC ∠=︒ ∵OB OC = ∴45OBC OCB ∠=∠=° ∴45BCH OBC ∠=∠=° 在Rt BHC △中，BC =可得sin45BH BC =⋅°3=，cos45CH BC =⋅°3= 在Rt BHP △中，3tan 4P =可得4tan BHPH P==∴5BP == ∴7PC PH CH =+= ∴PF PC =∴2FB PF PB PC PB =-=-= 方法二：解：如图，过点C 作CH AP ⊥于点H∵OB PC ∥，90OCP ∠=︒ ∴90BOC ∠=° ∵OB OC = ∴45OBC OCB ∠=∠=° 在Rt OBC △中，BC = 可得sin45OB BC =⋅°3= ∴3OE OB ==∵GBO P ∠=∠，3tan 4P =∴3tan 4GBO ∠=在Rt GBO △中，tan OG GBO GB ∠=，3OB = ∴95OG =，125GB =∴65EG OE OG =-= 在Rt CHP △中，tan CHP PH=，222CH PH PC +=设3CH x =，则4PH x =，5PC x = ∵PC PF = ∴FH PF PH x =-= ∵EFG CFH ∠=∠，90EGF CHF ∠=∠=o ∴EGF △∽CHF △ ∴13FG FH EG CH == ∴1235FG EG ==∴2FB GB FG =-=PPP方法三：解：如图，过点C 作CH AP ⊥于点H ，连接AC ∵OB PC ∥，90OCP ∠=︒ ∴90BOC ∠=︒ ∴1452A BOC ∠=∠=° 在Rt CHP △中，3tan 4CH P PH == 设3CH x =，则4PH x =，5PC x =在Rt AHC △中，45A ∠=°，3CH x = ∴3AH CH x ==，32AC x = ∴7PA AH PH x =+= ∵P P ∠=∠，45PCB A ∠=∠=︒ ∴PCB PAC △∽△ ∴PB PC BC PC PA AC ==∵32BC = ∴75x =，7PC =，5PB = ∵PF PC = ∴7PF = ∴2FB PF PB =-=方法四：解：如图，延长CO 交AP 于点M∵OB PC ∥，90OCP ∠=︒ ∴90BOC ∠=︒ 在Rt OBC △中，32BC =，OB OC = 可得3OB =∵MBO P ∠=∠，3tan 4P =∴3tan 4MBO ∠=在Rt MBO △中，3tan 4OM MBO OB ∠== 可得94OM =，154BM = ∴214CM = 在Rt PCM △中，3tan 4CM P PC ==可得7PC =，354PM = ∴5PB PM BM =-=，7PF PC == ∴2FB PF PB =-=4怀柔(1)∵点A 、C 、D 为O e 的三等分点 ∴»»»AD DC AC == ∴AD=DC=AC ∵AB 是O e 的直径 ∴AB ⊥CD ∵过点B 作O e 的切线BM∴BE ⊥AB ∴//CD BM(2) 连接DB由双垂直图形容易得出∠DBE=30°，在Rt △DBE 中，由DE=m ，解G H F APCBE OABCDF M O得BE=2m ，m②在Rt △ADB 中利用30°角，解得AB=2m ，③在Rt △OBE 中，由勾股定理得出④计算出△OB E 周长为2m 5通州（1）连接OC∵»»CB CB = ∴2BOC BAC ∠=∠∵∠ABD =2∠BAC ∴BOC ABD ∠=∠ ∴BD ∥OC ∵CE ⊥DB ∴CE ⊥OC ∴CF 是⊙O 的切线（2）解：连接AD∵AB 为⊙O 的直径 ∴BD ⊥AD ∵CE ⊥DB ∴AD ∥CF ∴F BAD ∠=∠ 在Rt △ABD 中 ∴3sin sin 5BD F=BAD AB ∠==. ∴18355AB = ∴6AB = ∴3OC = 在Rt △COF 中 ∴3sin 5OC F OF == ∴335OF = ∴5OF = 另解：过点O 作OG ⊥DB 于点G 6燕山 (1)连接OC ，∵PD 切⊙O 于点C ∴OC ⊥PC ∵AD ⊥PC 于点D ∴OC ∥AD ∴∠1＝∠3 又∵OA ＝OC ∴∠2＝∠3 ∴∠1＝∠2 即AC 平分∠DAB(2) 思路一：连接CE 可证Rt △CDE ∽Rt △ACB ∴DE CEBC AB=在Rt △ABC 中，由AB ＝10，sin ∠CAB ＝25，可求BC ＝4由∠1＝∠2，得EC ⌒＝BC ⌒ ∴EC ＝BC ＝4 故BC CEDE AB=g 可求思路二：过点B 作BF ⊥l 于点F ，连接BE ，可证四边形DEBF 是矩形 ∴DE ＝BF 由AB 为⊙O 的直径，∠ACB ＝90°，且OC ⊥PC 可证∠BCF ＝∠3＝∠2，在Rt △ABC 中，由AB ＝10，sin ∠2＝25，可求BC ＝4 在Rt △BCF 中，由BC ＝4，sin ∠BCF ＝sin ∠2＝25可求BF ＝85 ∴DE ＝BF ＝857房山）（1）证明：连结BC∵AB ，AC 是⊙O 的两条切线，B ，C 为切点∴=AB AC ,平分∠OA BAC ∴OA ⊥BC ∵CE 是⊙O 的直径 ∴∠CBE =90° ∴ OA ∥BE (2)∵OA ∥BE ∴∠BEO =∠AOC ∵tan ∠BEO∴tan ∠AOC在Rt △AOC 中,设OC =r ,则AC, OA∴在Rt △CEB 中,EBr ∵BE ∥OA ∴△DBE ∽△DAO ∴DE EB DO OA =2DO =∴DO =3AA8门头沟（1）∵ AB 是⊙O 的直径，BM 是⊙O 的切线 ∴ AB ⊥BM∵ CD ∥BM ∴AB ⊥CD ∴»»AD AC = ∵»»AD DC = ∴ »»»AD AC DC== ∴ AD =AC =DC ∴△ACD 是等边三角形（2）连接BD ，如图∵ AB 是⊙O 的直径 ∴∠ADB =90° ∵∠ABD =∠C =60°∴∠DBE =30° 在Rt △BDE 中，DE =2，可得BE =4，BD=在Rt △ADB 中，可得AB=∴ OB=在Rt △OBE 中，由勾股定理得OE=9大兴（1）连接OD∵OD =OA ∴∠ODA=∠OAD ∵CD ⊥AB 于点C ∴∠OAD +∠ADC =90° ∴∠ODA +∠ADC = 90° ∵∠PDA =∠ADC ∴∠PDA +∠ODA =90° 即∠PDO =90° ∴PD ⊥OD ∵D 在⊙O 上 ∴PD 是⊙O 的切线（2） ∵∠PDO =90° ∴∠PDC +∠CDO =90° ∵CD ⊥AB 于点C∴∠DOC +∠CDO =90° ∴∠PDC =∠DOC 4tan 3PDC ∠=Q 4tan 3DOC ∴∠= 设DC = 4x ,CO = 3x ,则OD =5x ∵AC =3 ∴OA =3x+3 ∴3x+3=5x ∴x =32∴OC=3x=92, OD=OB=5x =152∴BC=1210（2019.1+++平谷+++初三上+++期末）无答案ABEM ABEMB11朝阳12西城。

2019年1月北京海淀初三上数学期末试卷及答案

2019北京海淀初三（上）期末数学2019．01一、选择题（本题共16分，每小题2分） 1．抛物线213yx 的顶点坐标为（）A ．1,3B ．1,3 C ．1,3 D ．3,12．如图，在平面直角坐标系xOy 中，点43P ，，OP 与x 轴正半轴的夹角为α，则tan α的值为（）A ．35 B ．45 C ．34D ．433．方程230x x 的根的情况是（）A ．有两个不相等的实数根B ．有两个相等的实数根C ．无实数根D ．只有一个实数根4．如图，一块含30°角的直角三角板ABC 绕点C 顺时针旋转到△A B C ，当B ，C ，A 在一条直线上时，三角板ABC 的旋转角度为（） A ．150°B ．120°C ．60°D ．30°5．如图，在平面直角坐标系xOy 中，B 是反比例函数2(0)yx x的图象上的一点，则矩形OABC 的面积为（）A ．1B ．2C ．3D ．46．如图，在ABC △中，DE BC ∥，且DE 分别交AB ，AC 于点D ，E ，若:=2:3AD AB ，则△ADE 和△ABC 的面积．．之比等于（） A ．2:3 B ．4:9 C ．4:5 D7．图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A 与B 之间的距离为10cm ，双翼的边缘==AC BD 54cm ，且与闸机侧立面夹角PCA BDQ ∠=∠= 30°．当双翼收起时，可以通过闸机的物体的最大宽度为（）B'A'CAE D CBA图1 图2A．cm B．cm C ．64 cmD ． 54cm8．在平面直角坐标系xOy 中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（）A ．1y B. 2y C ．3y D. 4y 二、填空题（本题共16分，每小题2分） 9．方程230x x -=的根为．10．半径为2且圆心角为90°的扇形面积为．11．已知抛物线的对称轴是x n =，若该抛物线与x 轴交于10（，），30（，）两点，则n 的值为． 12．在同一平面直角坐标系xOy 中，若函数y x =与ky x=()0k ≠的图象有两个交点，则k 的取值范围是．13．如图，在平面直角坐标系xOy 中，有两点24A ，，40B ，，以原点O 为位似中心，把△OAB 缩小得到△OA B . 若B '的坐标为20，，则点A '的坐标为．14．已知1(1)y ，，2(2)y ，是反比例函数图象上两个点的坐标，且12y y ，请写出一个符合条件的反比例函数的解析式．15．如图，在平面直角坐标系xOy 中，点30A ，，判断在M N P Q ，，，四点中，满足到点O 和点A 的距离都小于2的点是．16．如图，在平面直角坐标系xOy 中，P 是直线2y 上的一个动点，⊙P 的半径为1，直线OQ 切⊙P 于点Q ，则线段OQ 的最小值为．三、解答题（本题共68分，第17~22题，每小题5分；第23~26题，每小题6分；第27~28题，每小题7分） 17．计算：0cos452sin302．18．如图，AD 与BC 交于O 点，AC ，4AO ，2CO ，3CD ，求AB 的长．19．已知x n 是关于x 的一元二次方程2450mx x 的一个根，若246mn n m ，求m 的值．20．近视镜镜片的焦距y （单位：米）是镜片的度数x （单位：度）的函数，下表记录了一组数据：（1）在下列函数中，符合上述表格中所给数据的是_________；A ．1100yx B ．100yxC ．13+2002y x D ．21319400008008x yx（2）利用（1）中的结论计算：当镜片的度数为200度时，镜片的焦距约为________米．21已知：如图，⊙O 及⊙O 上一点P . 求作：过点P 的⊙O 的切线．作法：如图，作射线OP ；② 在直线OP 外任取一点A ，以点A 为圆心，AP 为半径作⊙A ，与射线OP 交于另一点B ；ODCBA③ 连接并延长BA 与⊙A 交于点C ； ④ 作直线PC ；则直线PC 即为所求．根据小元设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明：证明：∵ BC 是⊙A 的直径，∴ ∠BPC =90°（____________）（填推理的依据）． ∴ OP ⊥PC ．又∵ OP 是⊙O 的半径，∴ PC 是⊙O 的切线（____________）（填推理的依据）．22．2018年10月23日，港珠澳大桥正式开通，成为横亘在伶仃洋上的一道靓丽的风景. 大桥主体工程隧道的东、西两端各设置了一个海中人工岛，来衔接桥梁和海底隧道，西人工岛上的A 点和东人工岛上的B 点间的距离约为5.6千米，点C 是与西人工岛相连的大桥上的一点，A ，B ，C 在一条直线上．如图，一艘观光船沿与大桥AC 段垂直的方向航行，到达P 点时观测两个人工岛，分别测得,PA PB 与观光船航向PD 的夹角∠DPA =18°，∠DPB =53°，求此时观光船到大桥AC 段的距离PD 的长．参考数据：sin18°0.31≈，cos18°0.95≈，tan18°0.33≈，sin53°0.80≈，cos53°0.60≈，tan53° 1.33≈．23．在平面直角坐标系xOy 中，已知直线12y x 与双曲线ky x的一个交点是(2,)A a ．（1）求k 的值；（2）设点()P m n ，是双曲线kyx上不同于A 的一点，直线PA 与x 轴交于点(,0)B b ． ①若1m ，求b 的值；②若=2PB AB ，结合图象，直接写出b 的值．24．如图，A ，B ，C 为⊙O 上的定点．连接AB ，AC ，M 为AB 上的一个动点，连接CM ，将射线MC 绕点M 顺时针旋转90，交⊙O 于点D ，连接BD ．若AB =6cm ，AC =2cm ，记A ，M 两点间距离为x cm ，B D ，两点间的距离为y cm ．小东根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小东探究的过程，请补充完整：（1）通过取点．．、画图．．、测量．．，得到了x 与y 的几组值，如下表：（3）结合画出的函数图象，解决问题：当BD =AC 时，AM 的长度约为 cm ．BA25．如图，AB 是⊙O 的弦，半径OE AB ， P 为AB 的延长线上一点，PC 与⊙O 相切于点C ，CE 与AB 交于点F ．（1）求证：PC =PF ；（2）连接OB ，BC ，若//OB PC ，BC =，3tan 4P =，求FB 的长. 26．在平面直角坐标系xOy 中，已知抛物线G ：224844y x ax a ，(1,0),(,0)A N n -．（1）当1a 时，①求抛物线G 与x 轴的交点坐标；②若抛物线G 与线段AN 只有一个交点，求n 的取值范围；（2）若存在实数a ，使得抛物线G 与线段AN 有两个交点，结合图象，直接写出n 的取值范围．27．已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD ．（1）如图1，① 求证：点,,B C D 在以点A 为圆心，AB 为半径的圆上. ② 直接写出∠BDC 的度数（用含α的式子表示）为___________.（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD ；（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转，当线段BF的长取得最大值时，直接写出tan FBC ∠的值．图1 图2 图3BB28．在平面直角坐标系xOy 中，已知点(0,)A a 和点(0)B b ，，给出如下定义：以AB 为边，按照逆时针方向排列A ，B ，C ，D 四个顶点，作正方形ABCD ，则称正方形ABCD 为点A ，B 的逆序正方形．例如，当4a ，3b 时，点A ，B 的逆序正方形如图1所示．图1 图2（1）图1中点C 的坐标为；（2）改变图1中的点A 的位置，其余条件不变，则点C 的坐标不变（填“横”或“纵”），它的值为；（3）已知正方形ABCD 为点A ，B 的逆序正方形.①判断：结论“点C 落在x轴上，则点D 落在第一象限内．”______（填“正确”或“错误”），若结论正确，请说明理由；若结论错误，请在图2中画出一个反例；②⊙T 的圆心为(,0)T t ，半径为1. 若4a ，0b ，且点C 恰好落在⊙T 上，直接写出t 的取值范围.。

2019 北京各区初三(上)期末数学分类汇编——代数综合

2019北京各区初三（上）期末数学分类汇编——代数综合1 昌平在平面直角坐标系xOy 中，抛物线 y ＝mx 2－4mx ＋4m －2 的顶点为M （1）顶点M 的坐标为_______ __（2）横、纵坐标都是整数的点叫做整点. 若MN ∥y 轴且MN = 2 ①点N 的坐标为_____________②过点N 作y 轴的垂线l ，若直线l 与抛物线交于P 、Q 两点，该抛物线在P 、Q 之间的部分与线段PQ 所围成的区域（包括边界）恰有七个整点，结合函数图象，求m 的取值范围 2 丰台在平面直角坐标系xOy 中，抛物线过点A （-1，0）（1）求抛物线的对称轴（2）直线与y 轴交于点B ，与该抛物线对称轴交于点C ，如果该抛物线与线段BC 有交点，结合函数的图象，求的取值范围 3 海淀在平面直角坐标系xOy 中，已知抛物线G ：224844y x ax a =-+-，(1,0),(,0)A N n − （1）当1a =时①求抛物线G 与x 轴的交点坐标 ②若抛物线G 与线段AN 只有一个交点，求n 的取值范围（2）若存在实数a ，使得抛物线G 与线段AN 有两个交点，结合图象，直接写出n 的取值范围 4 怀柔在平面直角坐标系xOy 中，抛物线22y ax ax c =++（其中a 、c 为常数，且a ＜0）与x 轴交于点A ()3,0−，与y 轴交于点B ，此抛物线顶点C 到x 轴的距离为4 （1）求抛物线的表达式（2）求CAB ∠的正切值（3）如果点P 是x 轴上的一点，且ABP CAO ∠=∠，直接写出点P 的坐标2+3y ax bx a =+4y x =+a在平面直角坐标系xOy 中，抛物线()240y ax ax m a =−+≠与x 轴的交点为A 、B ，（点A 在点B 的左侧），且AB =2（1）求抛物线的对称轴及m 的值(用含字母a 的代数式表示)（2）若抛物线()240y ax ax m a =−+≠与y 轴的交点在（0，-1）和（0，0）之间，求a 的取值范围（3）横、纵坐标都是整数的点叫做整点若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内（包括边界）恰有5个整点，结合函数的图象，直接写出a 的取值范围 6 房山在平面直角坐标系xOy 中，点()4,2A −−，将点A 向右平移6个单位长度，得到点B （1）直接写出点B 的坐标（2）若抛物线2y x bx c =−++经过点A ,B ，求抛物线的表达式（3）若抛物线2y x bx c =−++的顶点在直线2y x =+上移动，当抛物线与线段AB 有且只有一个公共点时，求抛物线顶点横坐标t 的取值范围 7 门头沟在平面直角坐标系xOy 中，抛物线22y x mx n =-++经过点A （0，2），B （3，4-）（1）求该抛物线的函数表达式及对称轴（2）设点B 关于原点的对称点为C ，点D 是抛物线对称轴上一动点，记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点），如果直线CD 与图象G 有两个公共点，结合函数的图象，直接写出点D 纵坐标t 的取值范围在平面直角坐标系中中，抛物线与y 轴交于点C ，当a=1时，该抛物线与x 轴的两个交点为A ，B （点A 在点B 左侧）（1）求点A ，B ，C 的坐标（2）若该抛物线与线段AB 总有两个公共点，结合函数的图像，求a 得取值范围 9 西城在平面直角坐标系中，已知抛物线（1）求抛物线的对称轴（2）当>0 时，设抛物线与x 轴交于A ，B 两点（点A 在点B 左侧），顶点为C ，若△ABC 为等边三角形，求的值（3）过T （0，t ）（其中）且垂直y 轴的直线与抛物线交于M ，N 两点. 若对于满足条件的任意t 值，线段 MN 的长都不小于1，结合函数图象，直接写出的取值范围 10 大兴已知抛物线（1）求证：该抛物线与x 轴总有交点（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 得取值范围（3）设抛物线与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线的对称点恰好是点M ，求m 的值xoy ()()02212≠−−+=a x a ax y xoy a ax ax y 342+−=a a 21≤≤−t l a ()m x m x y −+−+−=652()m x m x y −+−+−=652x y −=在平面直角坐标系中，抛物线经过点A ，B ，C ，已知A （-1,0）C （0,3）（1）求抛物线的表达式（2）如图1，P 为线段BC 上一点，过点P 作y 轴平行线，交抛物线于点D ，当的面积最大时，求点P 的坐标（3）如图2，抛物线顶点为E ，轴于F 点，N 是线段EF 上一动点，M （m ，0）是x 轴上一动点，若，直接写出实数m 的取值范围12 东城在平面直角坐标系中，抛物线的表达式为，线段AB 的两个端点分别为A （1,2）B （3,2）（1）若抛物线经过原点，求出m 的值（2）求抛物线顶点C 的坐标（用含有m 的代数式表示）（3）若抛物线与线段AB 恰有一个公共点，结合函数图像，求出m 的取值范围xoy c bx x y ++−=2BCD ∆x EF ⊥090=∠MNC xoy m m mx x y 224222+−+−=在平面直角坐标系xOy 中，抛物线y =ax 2+bx +3（a ≠0）经过（1,0），且与y 轴交于点C （1）直接写出点C 的坐标（2）求a ,b 的数量关系（3）点D （t ，3）是抛物线y =ax 2+bx +3上一点（点D 不与点C 重合） ①当t =3时，求抛物线的表达式 ②当3CD 4时，求a 的取值范围14. 石景山在平面直角坐标系xOy 中，直线(0)y kx b k =+≠与抛物线243y ax ax a =−+的对称轴交于点(1)A m −，，点A 关于x 轴的对称点恰为抛物线的顶点．（1）求抛物线的对称轴及a 的值；（2）横、纵坐标都是整数的点叫做整点．记直线(0)y kx b k =+≠与抛物线围成的封闭区域（不含边界）为W ．①当=1k 时，直接写出区域W 内的整点个数；②若区域W 内恰有3个整点，结合函数图象，求b 的取值范围．<<2019北京各区初三（上）期末数学分类汇编——代数综合参考答案1（2019.1+++昌平+++初三上+++期末）（1）M （2，-2）（2）①N （2,0）或N （2，-4） ②12＜m ≤1或1−≤m ＜12− 2（2019.1+++丰台+++初三上+++期末）（1）∵抛物线23y ax bx a =++过点A （-1，0） ∴30a b a −+= ∴4b a = ∴抛物线解析式可化为243y ax ax a =++ ∴抛物线的对称轴为422ax a=−=− （2）由题意，得B （0,4），C （-2,2）∵抛物线243y ax ax a =++过点A （-1，0）且抛物线的对称轴为2x =− 由抛物线的对称性可知，抛物线也一定经过A 的对称点（-3，0） ①0a >时，如图1将0x =代入抛物线得3y a = ∵抛物线与线段BC 有交点∴34a ≥，解得43a ≥②0a <时，如图2 将2x =−代入抛物线，得y a =− ∵抛物线与线段BC 有交点 ∴2a −≥，解得2a ≤−综上所述，423a a ≥≤−或3（2019.1+++海淀+++初三上+++期末）（1）①当1a =时，248y x x =− 当0y =时，2480x x −= 解得10x =，22x =∴抛物线G 与x 轴的交点坐标为()00，，()20， ②当0n =时，抛物线G 与线段AN 有一个交点当2n =时，抛物线G 与线段AN 有两个交点，结合图象可得02n ≤< （2）3n ≤−或1n ≥4（2019.1+++怀柔+++初三上+++期末）（1）由题意得，抛物线22y ax ax c =++的对称轴是直线212ax a=−=− ∵a ＜0，抛物线开口向下，又与x 轴有交点 ∴抛物线的顶点C 在x 轴的上方由于抛物线顶点C 到x 轴的距离为4，因此顶点C 的坐标是()1,4− 可设此抛物线的表达式是()214y a x =++由于此抛物线与x 轴的交点A 的坐标是()3,0−，可得1a =− 因此，抛物线的表达式是223y x x =−−+ （2）点B 的坐标是()0,3联结BC .∵218AB =，22BC =，220AC =，得222AB BC AC += ∴△ABC 为直角三角形，90ABC ∠= 所以1tan 3BC CAB AB ∠== 即CAB ∠的正切值等于13（3）点p 的坐标是（1，0）5（2019.1+++通州+++初三上+++期末）（1）对称轴为直线422ax a−=−= ∵AB =2，点A 在点B 的左侧 ∴A ()10,，B ()30, 把A （1，0）代入()240y ax ax m a =−+≠中 ∴3m a =（2）∵抛物线()2430y ax ax a a =−+≠与y 轴的交点在（0，-1）和（0，0）之间 ∴0a <当抛物线()2430y ax ax a a =−+≠经过点（0，-1）时，可得13a =− ∴a 的取值范围是103a −<< （3）32a −<−≤或2<3a ≤ 6（2019.1+++房山+++初三上+++期末）（1）()2,2B −（2）抛物线2y x bx c =−++过点,A B∴1642422b c b c −−+=−⎧⎨−++=−⎩ 解得26b c =−⎧⎨=⎩∴抛物线表达式为226y x x =−−+（3）抛物线2y x bx c =−++顶点在直线2y x =+上 ∴抛物线顶点坐标为(),2t t +∴抛物线表达式可化为()22y x t t =−−++ 把()4,2A −−代入表达式可得()2242t t −=−−−++解得123,4t t =−=−∴43t −≤<−把()2,2B −代入表达式可得()2222t t −−++=− 解得340,5t t ==∴05<≤t综上可知t 的取值范围时43t −≤<−或05<≤t 7（2019.1+++门头沟+++初三上+++期末）（1）∵点A ，B 在抛物线y =2x 2+mx +n 上 ∴22,4233.n m n =⎧⎨−=⨯++⎩解得4,2.m n =⎧⎨=⎩ ∴抛物线的表达式为y =－2x 2+4x +2 ∴抛物线的对称轴为x =1（2）43≤t ＜4 8（2019.1+++朝阳+++初三上+++期末）（1）当a=1时，抛物线为令解得∵点A 在点B 左侧 ∴A （-1,0），B （2,0）（2）①若抛物线开口向上，如图1，抛物线经过点A ，B ，此时A 的值最小，可求得a=1所有②若抛物线开口向下，如图2，当点B 为抛物线顶点时，抛物线与x 轴只有一个公共点，可求得，所以22−−=x x y ()20−∴，C 022=−−x x 2121=−=x x ，1≥a 21−=a 21−<a综上所述，A 的取值范围为或 9（2019.1+++西城+++初三上+++期末）（1）（2）∵为等边三角形（2）或 10（2019.1+++大兴+++初三上+++期末）（1）证明：()222454670b acm m m ∆=−=(−)+(−)=−≥所以方程总有两个实数根（2）由（1）()27m ∆=−，根据求根公式可知，方程的两根为：52m x −=−即1216x x m =−=−+，由题意，有365 <-m < + 13 < m ∴< (3)令 x = 0, y =6m −+ ∴M （0，6m −+）由（2）可知抛物线与x 轴的交点为（-1,0）和（6m −+,0）它们关于直线的对称点分别为（0 , 1）和（0, 6m −）由题意，可得：6166m m m −+=−+=−或 56m m ∴==或 11（2019.1+++顺义+++初三上+++期末）无答案 12（2019.1+++东城+++初三上+++期末）无答案1≥a 21−<a 2242=−−=−=aa ab x ()()31342−−=+−=x x a a ax ax y ()()()a -20,30,1，，，C B A ∴0>a 0<−∴a ABC ∆()32−∴，C 3−=−∴a 3=∴a 38−≤a 34≥a y x =−26.解：（1）∵抛物线经过原点,2120220, 1.2m m m m ∴=−+∴==分（2）222(2)2y x mx m m =−−++22()2x m m =−−+所以，顶点C 的坐标为(,2)m m ……………………4分（3）由顶点C 的坐标可知，抛物线的顶点C 在直线y=2x 上移动．当抛物线过点A 时，m=2或1；当抛物线过点B 时，m=2或5．所以m=2时，抛物线与线段AB 有两个公共点，不符合题意．结合函数的图象可知，m 的取值范围为15m ≤≤且2m ≠…………………6分 13（2019.1+++平谷+++初三上+++期末）无答案。

北京市各区县2019年初三数学期末试题分类汇编：几何综合

2019年1月期末试题分类汇编——几何综合（2018·石景山1月期末·25）将ABC △绕点A 按逆时针方向旋转,旋转角为）（︒<α<︒α900，旋转后使各边长变为原来的n 倍，得到C B A ''△,我们将这种变换记为[n ,α]．（1）如图①,对ABC △作变换[3,60 ]得C B A ''△，则C B A S ''△：ABC S △= ___；直线BC 与直线C B ''所夹的锐角为 __ °；（2）如图②，ABC △中，330,90==∠=∠AC BAC ACB ，，对ABC △ 作变换[n ,α]得C B A ''△，使得四边形C B AB ''为梯形，其中AB ∥C B '',且梯形C B AB ''的面积为312，求α和n 的值．25. 解：（1………………………………………2分（2）由题意可知：C B A ''△∽ABC △n BC C B AC C A C C =''='=∠='∠∴,90︒=∠∴90',''//BAC C B AB60-90=∠︒=α∴BAC ……………………………4分在ABC Rt △中,121230cos ====AB BC AC AB ，n C B n AC =''=∴,3'………………………………5分∴在直角梯形C B AB ''中，()C A C B AB S '''+=21()3123221=+=n n …………………………6分()舍去6,4-==∴n n ………………………………7分4,60==α∴n（2018·西城1月期末·24）已知：△ABC ，△DEF 都是等边三角形，M 是BC 与EF 的中点，连接AD ，BE. （1）如图1，当EF 与BC 在同一条直线上时，直接写出AD 与BE 的数量关系和位置关系；（2）△ABC 固定不动，将图1中的△DEF 绕点M 顺时针旋转α（o 0≤α≤o 90）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；（3）△ABC 固定不动，将图1中的△DEF 绕点M 旋转α（o 0≤α≤o 90）角，作DH⊥BC 于点H ．设BH ＝x ，线段AB ，BE ，ED ，DA 所围成的图形面积为S ．当AB ＝6，DE ＝2时，求S 关于x 的函数关系式，并写出相应的x 的取值范围．24．（1）ADBE=，AD BE⊥．........................................... 2分（2）证明：连接DM，AM．在等边三角形ABC中，M为BC的中点，∴ AM BC⊥，1302BAM BAC∠=∠=︒，AMBM∴ 90BME EMA∠+∠=︒．同理，DMEM，90AMD EMA∠+∠=︒．∴AM DMBM EM=，AM D BM E∠=∠．·3分∴ △ADM ∽△BEM．∴AD DMBE EM==...................................... 4分延长BE交AM于点G，交AD于点K．∴ M AD M BE∠=∠，BGM AGK∠=∠．∴ 90GKA AMB∠=∠=︒．∴ AD BE⊥．............................................ 5分（3）解：(ⅰ)当△DEF绕点M顺时针旋转α(o0≤α≤∵ △ADM ∽△BEM，∴ 2()3ADMBEMS ADS BE∆∆==．∴13BEM ADMS S∆∆=∴ABM ADM BEM DEMS S S S S∆∆∆∆=+--23ABM ADM DEMS S S∆∆∆=+-121133)12322x=⨯⨯⨯⨯--⨯=∴ S=（3≤x≤3+）．.......................... 6分(ⅱ) 当△DEF绕点M逆时针旋转α(o0≤α≤o90)角时，可证△ADM∽△BEM，∴ 21()3BEMADMS BMS AM∆∆==．∴13BEM ADMS S∆∆=．∴ABM BEM ADM DEMS S S S S∆∆∆∆=+--23ABM ADM DEMS S S∆∆∆=--21)32x=⨯⨯-+=∴ S =3≤x ≤3)．综上，S =(3≤x≤3+)． .......................... 7分（2018·海淀1月期末·24）已知四边形ABCD 和四边形CEFG 都是正方形，且AB>CE ．（1）如图1，连接BG 、DE ．求证：BG=DE ；（2）如图2，如果正方形ABCDCEFG 绕着点C 旋转到某一位置时恰好使得C G//BD ，BG=BD.①求BDE ∠的度数；②请直接写出正方形CEFG 的边长的值.24. （本小题满分7分）解：（1）证明：∵四边形ABCD 和CEFG 为正方形，∴BC DC =，CG CE =，90BCD GCE ∠=∠=︒. ∴BCD DCG GCE DCG ∠+∠=∠+∠.BCG DCE ∠=∠即：. (1)分∴△BCG ≌△DCE .∴BG D E =.………………………………2分（2）①连接BE .由（1）可知：BG=DE. ∵//CG BD ，∴=45D CG BD C ∠∠=︒.∴9045135BCG BCD G CD ∠=∠+∠=︒+︒=︒. ∵90G CE ∠=︒,∴36036013590135BCE BCG G CE ∠=︒-∠-∠=︒-︒-︒=︒. ∴=BCG BCE ∠∠.…………………………3分 ∵BC BC CG CE ==，, ∴△BCG ≌△BCE .∴BG BE =.………………………………4分∵BG BD DE ==,∴BD BE DE ==. ∴△BDE 为等边三角形.∴60.BDE ∠=︒ …………………………5分②正方形CEFG1. ……………………………………………7分（2018·朝阳1月期末·25）将△ABC 绕点B 逆时针旋转α(0°＜α＜180°)得到△DBE，直线DE 与直线AC 相交于点F ，连接BF ．（1）如图1，若α=60°，DF=2AF ，请直接写出BFAF等于；（2）若DF=mAF ，（m>0，且m≠1）①如图2，求BFAF；（用含α，m 的式子表示） ②如图3，依题意补全图形，请直接写出BFAF等于．（用含α，m 的式子表示）GFEDCBA图2ABCDEFG图1ABCDFG图1 图2 图325.解：（1）1． ………………………………1分（2）①如图2，在DF 上截取DG ，使得DG=AF ，连接BG ．由旋转知，DB=AB ，∠D=∠A．∴△DBG≌△ABF．∴BG=BF，∠GBF=α． ………………3分过点B 作BN⊥GF ∴点N 为GF 中点，∠FBN=2α．在Rt△BNF 中，NF=2sin α⋅BF ，∴GF=sin2α⋅BF∵DF=DG+GF， ……………………4分∴mAF=AF+22αBF(m-1)AF=2BF 注明：以上各题的其它的正确解法，酌情给分.图3图2（2018·东城1月期末·24）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中90,C ∠=︒30B E ∠=∠=︒.（1）操作发现如图2，固定△ABC ，使△DEC 绕点C 顺时针旋转．当点D 恰好落在AB 边上时，填空：图1 ① 线段DE 与AC 的位置关系是；② 设△BDC 的面积为1S ，△AEC 的面积为2S ，则1S 与2S 的数量关系是，证明你的结论；（2）猜想论证当△DEC 绕点C 旋转到图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中BC ，CE 边上的高，请你证明小明的猜想．图324．解：（1）①线段DE 与AC 的位置关系是平行． …………………..1分 ②S 1与S 2的数量关系是相等．证明：如图2，过D 作DN ⊥AC 交AC 于点N ，过E 作EM ⊥AC 交AC 延长线于M ，过C 作CF ⊥AB 交AB 于点F ．由①可知 △ADC 是等边三角形，DE ∥AC ， ∴DN=CF, DN=EM ． ∴CF=EM ．∵90,30ACB B ∠=︒∠=︒，∴2AB AC =．又∵AD AC =,∴BD AC =．图2∵112S CF BD =，212S AC EM =，∴1S =2S ． …………………..3分（2）证明：如图3，作DG ⊥BC 于点G ，AH ⊥CE 交EC 延长线于点H.∵90,180DCE ACB DCG ACE ∠=∠=︒∴∠+∠=︒．又∵180,ACH ACE ACH DCG ∠+∠=︒∴∠=∠．又∵90,CHA CGD AC CD ∠=∠=︒=,∴△AHC ≌△DGC ．∴AH=DG ．BDBD又∵CE=CB, 图3 ∴12S S =． ……………………..7分（2018·丰台1月期末·25）已知ABD ∆和CBD ∆关于直线BD 对称(点A 的对称点是点C )，点E 、F 分别是线段BC 和线段BD 上的点，且点F 在线段EC 的垂直平分线上，联结AF 、AE ，AE 交BD 于点G ．（1）如图（1），求证：ABD EAF ∠=∠；（2）如图（2），当AD AB =时，M 是线段AG 上一点，联结BM 、ED 、MF ，MF 的延长线交ED 于点N ，BAF MBF ∠=∠21，AD AF 32=，试探究线段FM 和FN 之间的数量关系，并证明你的结论．图（1）图（2）25. (1)证明：如图1 连接FE 、FC∵点F 在线段EC 的垂直平分线上,∴ FE=FC ∴∠l=∠2 ………………………1分∵△ABD 和△CBD 关于直线BD 对称． ∴AB=CB ,∠4=∠3，又BF=BF∴△ABF≌△CBF， ∴∠BAF=∠2，FA=FC∴FE=FA，∠1=∠BAF． …………………………2分 ∴∠5=∠6，∵ ∠l+∠BEF=1800，∴∠BAF+∠BEF=1800∵∠BAF+∠BEF+∠AFE+∠ABE=3600∴∠AFE+∠ABE=1800………………………………3分又∵∠AFE+∠5+∠6=1800， ∴∠5+∠6=∠3+∠4 ∴∠5=∠4，即∠EAF=∠ABD………………………4分(2)解：FM=72FN ……………………………………………5分证明：如图2，由(1)可知∠EAF=∠ABD，又∵∠AFB=∠GFA ∴△AFG∽△BFA ∴∠AGF=∠BAF又∵∠MBF=12∠B AF ，∴∠MBF=12∠AGF 又∵∠AGF=∠MBG+∠BMG∴∠MBG=∠BMG∴BG=MG…………………………6分 ∵AB=AD ∴∠ADB=∠ABD=∠EAF又∵∠FGA=∠AGD．∴△AGF∽△DGA．GF AG AFGA DG DA∴==∵AF=23AD 23GF AG GA DG ∴== 图2 G FEDCBA NMGF EDBA设GF=2a ，则AG=3a ， ∴GD=92a ，∴FD=DG -GF=922a a -=52a ∵∠CBD=∠ABD ，∠ABD=∠ADB，∴∠CBD=∠ADB. ∴//BE AD ．∴BG EG GD AG =23EG AG BG GD ∴==，设EG=2k ，则MG=BG=3k 过点F 作FQ∥ED 交AE 于Q ，24552GQ GF a a QE FD ∴=== 45GQ QE ∴=……………………7分∴GQ=49EG=89k ．∴QE=109k ， MQ=MG+GQ=3k+89k =359k ∵FQ∥ED，35791029kMF MQ FN QE k ∴===.∴FM=72FN ……………8分（2018·昌平1月期末·25）已知：四边形ABCD 中，AD ∥BC ，AD=AB=CD ，∠BAD=120°，点E 是射线CD 上的一个动点（与C 、D 不重合），将△ADE 绕点A 顺时针旋转120°后，得到△ABE'，连接EE'. （1）如图1，∠AEE'= °；（2）如图2，如果将直线AE 绕点A 顺时针旋转30°后交直线BC 于点F ，过点E 作EM ∥AD 交直线AF 于点M ，写出线段DE 、BF 、ME 之间的数量关系；（3）如图3，在（2）的条件下，如果CE=2，AE=ME 的长.25．解：(1) 30°. …………………………………………………… 1分(2)当点E 在线段CD 上时，2DE BF M E +=； ………………………………………… 2分当点E 在CD 的延长线上，030EAD ︒<∠<︒时，2BF DE M E -=； ………………… 3分3090EAD ︒<∠≤︒时，2DE BF M E +=； 90120EAD ︒<∠<︒时，2DE BF M E -=. …………………………………………4分(3)作AG BC ⊥于点G, 作DH BC ⊥于点H.由AD ∥BC ，AD=AB=CD ，∠BAD=120°，得∠ABC=∠DCB=60°，易知四边形AGHD 是矩形和两个全等的直角三角形ABG DCH ∆∆，.则GH=AD , BG=CH. ∵120ABE ADC '∠=∠=︒,E'MF ED CBA E'ED BA图1图2E'MF ED BA 图3∴点E '、B 、C 在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=12x ,. 作EQ BC ⊥于Q.在Rt △EQC 中，CE=2, 60C ∠=︒, ∴1CQ =, EQ ∴E'Q=21233BC CQ BE x x x '-+=-+-=-.…………………………………5分作AP EE '⊥于点P.∵△ADE 绕点A 顺时针旋转120°后，得到△ABE'.∴△A EE'是等腰三角形，30,AE E AE AE ''∠=︒==. ∴在Rt △AP E'中，∴EE'=2 E'P=……………………………………………………………………6分 ∴在Rt △EQ E'中，9=. ∴339x -=.∴4x =. ………………………………………………………… 7分 ∴2,8DE BE BC '===，2BG =. ∴4E G '=在Rt △E'AF 中,AG BC ⊥,∴Rt △AG E'∽Rt △FA E'. ∴AE E FE G AE ''=''∴7E F '=.∴5BF E F E B ''=-=. 由（2）知：2DE BF M E +=. ∴72ME =. ………………………………………………………… 8分（2018·怀柔1月期末·24）（1）如图1，在等边△ABC 中，点M 是边BC 上的任意一点（不含端点B 、C ），联结AM ，以AM 为边作等边△AMN，联结CN ．求证：∠ABC=∠ACN．[: 【类比探究】（2）如图2，在等边△ABC 中，点M 是边BC 延长线上的任意一点（不含端点C ），其它条件不变，（1）中结论∠ABC=∠ACN 还成立吗？请说明理由．【拓展延伸】PQ ACDEF ME'H G图1B图2C图3B图1B 图2C图3B（3）如图3，在等腰△ABC 中，BA=BC ，点M 是边BC 上的任意一点（不含端点B 、C ），联结AM ，以AM 为边作等腰△AMN，使顶角∠AMN=∠ABC．联结CN ．试探究∠ABC 与∠ACN 的数量关系，并说明理由．24.（（本小题满分7分）（1）证明：∵△ABC、△AMN 是等边三角形，∴AB=AC，AM=AN ，∠BAC=∠MAN=60°，∴∠BAM=∠CAN， ∴△BAM≌△CAN（SAS ），………………………………1分 ∴∠ABC=∠ACN．………………………………2分（2）结论∠ABC=∠ACN 仍成立．………………………………3分理由如下：∵△ABC、△AMN 是等边三角形，∴AB=AC，AM=AN ， ∠BAC=∠MAN=60°，∴∠BAM=∠CAN，∴△BAM≌△CAN（SAS ），………………………………4分 ∴∠ABC=∠ACN．………………………………5分（3）∠ABC=∠ACN．理由如下：∵BA=BC，MA=MN ，顶角∠ABC=∠AMN，∴底角∠BAC=∠MAN，∴△ABC∽△AMN，……………………6分 ∴=，又∵∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，∴∠BAM=∠CAN，∴△BAM∽△CAN，∴∠ABC=∠ACN．………………………………7分（2018·顺义1月期末·24）如图，ABC △和ADE △都是以A 为直角顶点的等腰直角三角形，连结BD ，BE ，CE ，延长CE 交AB 于点F ，交BD 于点G ．（1）求证：AFC GFB △∽△；（2）若ADE △是边长可变化的等腰直角三角形，并将ADE △绕点GF E DCBADGFE C B AD (G )FECB A D(G )(F)ECB AA 旋转，使CE 的延长线始终与线段BD （包括端点B 、D ）相交．当BDE △为等腰直角三角形时，求出AB BE ∶的值．24．解：（1）证明：∵9090BAC DAE ∠=∠=°，°， ∴90DAB BAE BAE EAC ∠+∠=∠+∠=°．∴DAB EAC ∠=∠．…………………………………………………1分 ∵AD AE =，且AB AC =， ∴ADB AEC △≌△，∴DBA ECA ∠=∠．…………………………………………………2分又GFB AFC ∠=∠， …………………………………………… 3分 ∴AFC GFB △∽△．………………………………………………4分（2）解：∵AFC GFB △∽△，∴90FGB FAC ∠=∠=°．①当90DEB ∠=°，DE=BE 时，如图①所示，设AD=AE=x，则DE =．∵BDE △为等腰直角三角形，∴BE DE ==．∴2BD x =．∵45ADB ADE EDB ∠=∠+∠=°+4590︒=°，图①∴AB =．∴AB BE ∶= ……………………………………………5分 ②当90EDB ∠=°，DE=DB 时，如图②所示，同理设AD=AE=x，则DE BD ==． ∴2BE x =． ∵90AEB ∠=°，∴AB ==．∴2AB BE ∶=． ……………… 6分图② ③当90DBE ∠=°，BD=BE 时，如图③所示，同理设AD=AE=x，则DE =．∴BD=BE=x ．∴四边形ADBE 是正方形，∴AB DE =．∴ABBE ∶=1． …………7分图③ （2018·延庆1月期末·24）如图①，已知点O 为菱形ABCD 的对称中心，∠A =60°，将等边△OEF 的顶点放在点O 处，OE ，OF 分别交AB ，BC 于点M ，N.（1）求证：OM=ON ；（2）写出线段BM ，BN 与AB 之间的数量关系，并进行证明；（3）将图①中的△OEF 绕O 点顺时针旋转至图②所示的位置，请写出线段BM ，BN与AB 之间的数量关系，并进行证明.24.（1）证明：取BC 的中点G ，连接OG ∵菱形ABCD,∠A =60°∴∠A =∠C=∠A BD=60°,AB=BC=CD=DA ……1分 ∵点O 为菱形ABCD 的对称中心 ∴OD=OB∴12OG CD =，OG//CD ………………2分 ∴∠BGO=∠C=60°, OG=OB∵等边△OEF ∴∠EOF=60° ∴∠1=∠2 ∵∠BGO=∠A BD=60° ∴△OBM ≌△OGN∴OM=ON ………………3分 (2)由（1）可知，BM=NG∵OB=OD ，BG=GC ∴12BG BC =∵BG=BN+NG ，AB=BC ∴12BN NG AB += ………………5分（3）取BC 中点G 同理可证：∴△OBM ≌△OGN ∴BM=GN ………………6分 ∴BG=BN-NG ∵12BG BC = ∴12BN NG AB -= ………………7分图②CA图① AC。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019九上代数综合题
2019昌平
26．在平面直角坐标系xOy 中，抛物线 y ＝mx 2－4mx ＋4m －2 的顶点为M . （1）顶点M 的坐标为_______ __.
（2）横、纵坐标都是整数的点叫做整点. 若MN ∥y 轴且MN = 2.
①点N 的坐标为_____________；
②过点N 作y 轴的垂线l ，若直线l 与抛物线交于P 、Q 两点，该抛物线在P 、Q 之间的部分与线段PQ 所围成的区域（包括边界）恰有七个整点，结合函数图象，求m 的取值范围.
2019朝阳
27．在平面直角坐标系xOy 中，抛物线2
(12)2y ax a x =+--(0)a ≠与y 轴交于点C .当1a =时，抛物线与x 轴交于点A ，B （点A 在点B 左侧）
．（1）求点A ，B ，C 的坐标；
（2）若该抛物线与线段AB 总有两个公共点，结合函数的图象，求a 的取值范围.
2019大兴
26．已知抛物线2
56y x m x m =--+-+（）. （1）求证：该抛物线与x 轴总有交点；
（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 的取值范围；
（3）设抛物线256y x m x m =--+-+（）与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ，求m 的值.
2019东城
26 . 在平面直角坐标系xOy 中，抛物线的表达式为2
2
2422y x mx m m =-+-+，线段AB 的两个端点分别为A （1，2），B （3，2） (1) 若抛物线经过原点，求出m 的值；
(2)求抛物线顶点C 的坐标（用含有m 的代数式表示）；
(3)若抛物线与线段AB 恰有一个公共点，结合函数图象，求出m 的取值范围.
2019房山
26. 在平面直角坐标系xOy 中，点()4,2A --，将点A 向右平移6个单位长度，得到点B . （1）直接写出点B 的坐标；
（2）若抛物线2
y x bx c =-++经过点A ,B ，求抛物线的表达式；
（3）若抛物线2
y x bx c =-++的顶点在直线2y x =+上移动，当抛物线与线段AB 有且只有一个公共点时，求抛物线顶点横坐标t 的取值范围．
2019海淀
26．在平面直角坐标系xOy 中，已知抛物线G ：224844y
x ax a ，(1,0),(,0)A N n -．
（1）当1a 时，
①求抛物线G 与x 轴的交点坐标；
②若抛物线G 与线段AN 只有一个交点，求n 的取值范围；
（2）若存在实数a ，使得抛物线G 与线段AN 有两个交点，结合图象，直接写出n 的取
值范围．
2019怀柔
26. 在平面直角坐标系xOy 中，抛物线22y ax ax c =++（其中a 、c 为常数，且a ＜0）与
x 轴交于点A ()3,0-，与y 轴交于点B ，此抛物线顶点C 到x 轴的距离为4．（1）求抛物线的表达式；（2）求CAB ∠的正切值；
（3）如果点P 是x 轴上的一点，且ABP CAO ∠=∠，直接写出点P 的坐标．
2019门头沟
26．在平面直角坐标系xOy 中，抛物线22y x mx n 经过点A （0，2），B （3，4）．
（1）求该抛物线的函数表达式及对称轴；
（2）设点B 关于原点的对称点为C ，点D 是抛物线对称轴上一动点，记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点），如果直线CD 与图象G 有两个公共点，结合函数的图象，直接写出点D 纵坐标t 的取值范围．
2019平谷
x
y
O
26．在平面直角坐标系xOy 中，抛物线y =ax 2+bx +3（a ≠0）经过（1,0），且与y 轴交于点C ．
（1）直接写出点C 的坐标；（2）求a ,b 的数量关系；
（3）点D （t ，3）是抛物线y =ax 2+bx +3上一点（点D 不与点C 重合）．
①当t =3时，求抛物线的表达式； ②当3<CD <4时，求a 的取值范围．
2019石景山
26．在平面直角坐标系xOy 中，直线(0)y kx b k =+≠与抛物线243y ax ax a =-+的对
称轴交于点(1)A m -，
，点A 关于x 轴的对称点恰为抛物线的顶点．（1）求抛物线的对称轴及a 的值；
（2）横、纵坐标都是整数的点叫做整点．记直线(0)y kx b k =+≠与抛物线围成的封
闭区域（不含边界）为W ．
①当=1k 时，直接写出区域W 内的整点个数；
②若区域W 内恰有3个整点，结合函数图象，求b 的取值范围．
2019通州
25. 在平面直角坐标系xOy 中，抛物线()2
40y ax ax m a =-+≠与x 轴的交点为A 、B ，（点
A 在点
B 的左侧），且AB =2.
（1）求抛物线的对称轴及m 的值(用含字母a 的代数式表示)；
（2）若抛物线()2
40y ax ax m a =-+≠与y 轴的交点在（0，-1）和（0，0）之间，求a
的取值范围；
（3）横、纵坐标都是整数的点叫做整点．
若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内（包括边界）恰有5个整点，结合函数的图象，直接写出a 的取值范围．
2019西城
26．在平面直角坐标系xOy 中，已知抛物线．（1）求抛物线的对称轴；
（2）当a >0时，设抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧），顶点为C ，若△ABC
为等边三角形，求a 的值；
（3）过点T （0，t ）（其中≤t ≤2）且垂直y 轴的直线l 与抛物线交于M ，N 两点，若
对于满足条件的任意t 值，线段MN 的长都不小于1，结合函数图象，直接写出a 的取值范围．
2019丰台
26．在平面直角坐标系xOy 中，抛物线过点A （-1，0）.
（1）求抛物线的对称轴；
（2）直线与y 轴交于点B ，与该抛物线对称轴交于点C ，如果该抛物线与线
段BC 有交点，结合函数的图象，求的取值范围．
2019密云
243y ax ax a =-+1
-2
+3y ax bx a =+4y x =+a
26.已知抛物线2
44+1
0)y ax ax a a =-+≠（与y 轴交于点A ，点A 与点B 关于抛物线的对称轴对称.直线l 经过点B 且与x 轴垂直.
（1）求抛物线的顶点C 的坐标和直线l 的表达式.
（2）抛物线与直线l 交于点P ，当OP ≤5时，求a 的取值范围.。