K-Hessian方程的一个Liouville型结果
热分析 Icepak V0.3

杨建林 (yangjianlin@)
2010 年 4 月 5 日 Rev. 0.3 beta
本文版本号为 0.3,一共收录有 129 个问题。如果大家有任何疑问可以到 米克仿真论坛 上参 与讨论。如果你对 FAQ 中的问题有自己的看法,欢迎到 米克仿真论坛 上提出,或者联系本文 档的维护人。在经过确认以后,你的方法将被收录到 FAQ 的新版本中。本文档会不定期更新, 并在 米克仿真论坛 提供最新版下载。 本文档的主要目的是帮助你快速的找到问题的答案,因此可能不是非常详细。如果你想系统 的学习 Icepak 请参考专门的资料 (见 问题 128 ) 。 本文档使用 Latex 系统排版,采用 CTX faq 这份文档的模板,对模板作者吴凌云表示感谢。
目录 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 C 建模 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 My model is very complicated, what is the best way to build it? . . . . . . . . . . How can I simplify my model? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Icepak 支持哪些建模方式? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 如何设定环境温度? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Icepak 快捷键及鼠标操作 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Opening 和 Grill 有什么区别,通风口改用什么建模? . . . . . . . . . . . . . . . . Plate 和 Block 有什么区别?Plate 有厚度,看起来也是一个体啊。 . . . . . . . . 求解区域大概设多大才合适? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Icepak 中可以画曲面吗? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . How large should my cabinet be? . . . . . . . . . . . . . . . . . . . . . . . . . . . Cabinet 的缺省特性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 怎么在 Block 上建孔特征? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对齐工具如何使用? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 模型的优先级有何作用,如何调整优先级? . . . . . . . . . . . . . . . . . . . . . . 如何设置散热器的接触热阻? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 排气式和吸入式风扇各有什么特点? . . . . . . . . . . . . . . . . . . . . . . . . . My package is not surrounded by walls on all sides, is it OK to use the cabinet walls or should I put openings on these walls? . . . . . . . . . . . . . . . . . . . . Should I include the effect of gravity in my model? . . . . . . . . . . . . . . . . . How accurate is a CFD solution? . . . . . . . . . . . . . . . . . . . . . . . . . . . How do I verify that the solution is correct? . . . . . . . . . . . . . . . . . . . . . What is the difference between laminar flows and turbulent flows? . . . . . . . . . What are turbulence models? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . What is conjugate heat transfer? . . . . . . . . . . . . . . . . . . . . . . . . . . . 雷诺数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 层流和紊流 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 热阻 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 常用的散热方式有哪些? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 风冷散热原理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 温度对电子元器件有哪些影响? . . . . . . . . . . . . . . . . . . . . . . . . . . . . 风道的设计原则 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 什么情况下需考虑辐射换热? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 什么情况下需使用强迫风冷方式散热? . . . . . . . . . . . . . . . . . . . . . . . . 风扇噪音与转速有何关系? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 湍流模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . k-ε 模型中的 K 和 ε 物理意义 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 7 8 8 8 8 9 9 10 11 11 11 12 12 12 13 14 15 15 16 16 16 16 18 18 18 18 18 18 18 19 19 19 20 20 20 2
K-Hessian方程的一个Liouville型结果

K-Hessian方程的一个Liouville型结果【摘要】本文研究了K-Hessian方程的一个Liouville型结果,首先介绍了K-Hessian方程的定义和性质,然后讨论了K-Hessian方程解的存在性。
接着我们详细阐述了K-Hessian方程的Liouville型结果以及相关证明方法。
进一步探讨了这一结果的意义,并展望了未来的研究方向。
通过本文的研究,我们得出了K-Hessian方程的一个Liouville型结果对于微分几何领域的重要意义,为相关领域的研究提供了新的思路。
【关键词】K-Hessian方程, Liouville型结果, 正定Hessian矩阵, 解的存在性, 相关证明方法, 研究背景, 研究目的, 研究意义, 结论总结, 未来研究展望1. 引言1.1 研究背景K-Hessian方程是极小曲面理论中一个重要的方程,它在几何分析和偏微分方程领域有着广泛的应用。
研究K-Hessian方程可以帮助我们更好地理解曲面的性质和演化。
在过去的研究中,学者们已经取得了一些有趣的结果,但仍然存在许多未解决的问题。
深入研究K-Hessian方程及其相关的Liouville型结果具有重要的理论意义和实际意义。
1.2 研究目的研究目的: 本文旨在探讨K-Hessian方程的一个Liouville型结果,通过分析K-Hessian方程的性质、解的存在性以及相关证明方法,进一步揭示该方程的特殊性质和数学规律。
我们的研究目的是为了揭示K-Hessian方程在几何分析和微分方程领域中的重要性,并为更深入的研究和应用提供理论基础。
通过研究K-Hessian方程的Liouville型结果,我们希望能够拓展对该方程解的理解,揭示其在几何学和物理学中的应用意义,为解决相关问题提供新的思路和方法。
我们将以严谨的数学推导和分析方法,探讨K-Hessian方程的Liouville型结果及其意义,为深入理解和应用K-Hessian方程奠定理论基础。
浅谈线性方程组的数值解法及其应用

浅谈线性方程组的数值解法及其应用1、相关定义1.1、分形油藏基本概念定义3.1[32]:维数为的分形渗透网嵌入到d(d=2,3)维岩块中,即整个导流系统是一个分形体,称具有这种特性的油藏为分形油藏。
df 3.1.1 分形孔隙度θf和渗透率Kf (r) 假设分形体内流体储集在体积为的座点处(设每个座点体积相同),座点密度为。
分形体中,座点孔隙体积为常数。
用描述某种相应对称性(如, Vs N( r ) Vs B B= A 2π h和4π 分别描述直线对称,圆柱面对称和球对称),a为位置-浓度参数[33], 为岩块的欧几里德维数,定义分形孔隙度d θf有: θf= aBVs rdf ?d (3-1) 这说明分形网格的θf 不再是常数,而是随波及半径r 成幂律关系。
取,则有: w r =r df d f w w r θ θr θw=aVBs rwd f ? d,得到分形孔隙度= ,θw 为r = rw 处的孔隙度。
同样渗透率定义为:Kf( r)= aVsB m rd f ?d ? θ (3-2) ( ) r= rw处的渗透率Kw=aVs Bm r wdf ?d ?θ ,得到渗透率Kf r= Kw rrw d f? d ?θ 。
3.1.2 分形参数的物理意义(1)分形维数df 分形维数df 严格地是一个分形体的几何特征,是分形体复杂程度的重要标志。
一般认为,d f值不同,复杂程度也不一样。
随复杂程度加剧,d f 值会愈高。
151.2、分数阶的基本定义从十七世纪分数阶微积分诞生之日起,数学家们就不断的探讨分数阶算子的理论体系。
后经多位数学家的努力,从不同的角度入手,建立了多种不同形式的分数阶算子定义,现在主要通用的三种定义[1]形式为: (1). Grümwald-Letnikov 定义:对于任意的实数α ,记α 的整数部分为[α ] ([α ] 为小于α 的最大整数),假如函数f ( t ) 在区间[α,t ]上有m+ 1 阶连续的导数,α > 0 时, m 至少取[α ],则定义分数阶α 阶导数为: ( ) li0m 0 ( ) n G aD tα f tΔ nhh→ =t ?a h ?α i =∑ ??? ?iα ??? f t ? ih (1-1) ( )( 1)( 2) ( 1) ! i i i 其中,?α = ?α ?α + ?α + L ?α + ? 。
K-Hessian方程的一个Liouville型结果

K-Hessian方程的一个Liouville型结果1. 引言1.1 K-Hessian方程的背景介绍K-Hessian方程是一个重要的偏微分方程,在几何分析和非线性偏微分方程研究中起着重要的作用。
它最早由美国数学家D.C.中提出,在几何分析中有广泛的应用。
K-Hessian方程是一个高阶非线性椭圆型偏微分方程,它的解与曲率和Hessian矩阵之间的关系密切相关。
K-Hessian方程在几何学、概率论、最优控制理论等领域都有着重要的应用。
研究K-Hessian方程的Liouville型结果对于理解非线性偏微分方程的性质和解的结构具有重要意义。
Liouville型结果是指:满足一定约束条件下的非负解的结构和分类。
通过研究K-Hessian方程的Liouville型结果,可以揭示解的性质、特征和分布规律,进一步推动相关领域的理论研究和应用发展。
探讨K-Hessian方程的Liouville型结果对于推动数学领域的发展具有重要意义。
1.2 Liouville型问题的研究意义1.在微分几何中,Liouville型问题可以帮助我们更深入地理解曲率的性质和几何结构。
通过研究Liouville型问题,可以揭示曲率与几何流形的关系,从而推动微分几何理论的发展。
Liouville型问题在数学领域中扮演着重要的角色,其研究意义不仅限于理论层面,还涉及到实际问题的建模和解决。
深入研究Liouville型问题将有助于推动数学领域的发展并解决实际问题。
2. 正文2.1 K-Hessian方程的定义与性质K-Hessian方程是一类非线性椭圆型偏微分方程,具有重要的数学和物理背景。
它的定义与性质包括以下几个重要方面:1. K-Hessian方程的定义:K-Hessian方程是指具有如下形式的二阶非线性椭圆型偏微分方程:\[ F(D^2u)=f(x,u,Du) \]\( F(D^2u) \)表示Hessian矩阵的K-拉普拉斯算子,由方程中的K 决定,通常表达为对Hessian矩阵的第K大本征值的求和,而\( f(x,u,Du) \)为给定的非线性项。
数理方程Sturm-Liouville问题

在前面几节中,我们讨论过常微分方程 X ''( x) X ( x) 0 的固有值问题 以后,我们还将研究如下的方程
d dy v2 ( x ) ( x ) y 0 dx dx x
d 2 dy (1 x ) y 0 dx dx
第三章 Sturm-Liouville问题
2
d dy ( p ( x) ) ( ( x) q ( x )) y 0 dx dx
S-L型方程附加上齐次的第一类、第二类、第三类边 界条件,或者是自然边界条件,就构成S-L型固有值 问题 称为固有值 满足S-L型方程及相应的边界条件的非零解就是固 有函数
第三章 Sturm-Liouville问题
4
Sturm-Liouville固有值问题的共有性质
d dy ( p( x) ) ( ( x) q( x)) y 0, x [a, b] 加上合适的边界条件 dx dx
性质5 固有函数系 yn ( x)在区间构成一个完备的正交 函数系. 即:函数f(x)如果具有连续一阶导数和逐段连 续二阶导数敛的级数
n
f n (n 1,2,) 叫做 f ( x) 的广义傅里叶系数
b
即
( x) f ( x) y ( x)dx
n
f n ( x)
a
b 2 ( x ) y n ( x ) dx a
.
第三章 Sturm-Liouville问题
6
d d
贝赛尔方程
d sin sin 0 勒让德方程 d
它们都可以归纳为下面的一般形式
d dy ( p ( x) ) ( ( x) q ( x )) y 0 dx dx
liouville函数

liouville函数Liouville函数是数论中的一个重要函数,它是一个周期为1的函数,其定义如下:$$\lambda(n) = (-1)^{\omega(n)}$$其中,$\omega(n)$表示$n$的不同质因数的个数。
Liouville函数最早由法国数学家Liouville在19世纪提出,它在数论中有着广泛的应用。
下面我们来看一下Liouville函数的一些性质。
Liouville函数的值只有两种可能,即$1$和$-1$。
当$n$的不同质因数的个数为偶数时,$\lambda(n)=1$;当$n$的不同质因数的个数为奇数时,$\lambda(n)=-1$。
Liouville函数是一个完全积性函数,即对于任意的正整数$m$和$n$,有$\lambda(mn)=\lambda(m)\lambda(n)$。
这个性质在数论中有着重要的应用,例如在研究数论中的一些问题时,可以通过将一个数分解成若干个质数的积,然后利用Liouville函数的完全积性来简化问题。
Liouville函数还有一个重要的性质,即对于任意的正整数$n$,有$$\sum_{d|n}\lambda(d) =\begin{cases}1 & \text{if } n=1 \\0 & \text{if } n>1\end{cases}$$这个性质被称为Liouville反演公式,它在数论中也有着广泛的应用。
例如,在研究数论中的一些问题时,可以通过利用Liouville反演公式将一个问题转化为求Liouville函数的和的问题,然后再利用Liouville函数的性质来解决问题。
Liouville函数是数论中的一个重要函数,它具有周期性、完全积性和Liouville反演公式等重要性质,这些性质在数论中有着广泛的应用。
因此,研究Liouville函数的性质和应用是数论研究的一个重要方向。
2010下-化工热力学期末考试闭卷A及答案
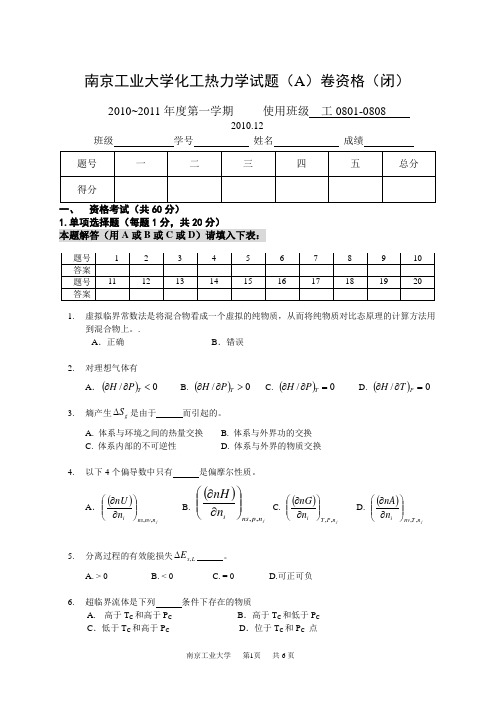
南京工业大学化工热力学试题(A )卷资格(闭)2010~2011年度第一学期 使用班级 工0801-08082010.12班级 学号 姓名 成绩1.单项选择题(每题1分,共20分)本题解答(用A 或B 或C 或D )请填入下表:1. 虚拟临界常数法是将混合物看成一个虚拟的纯物质,从而将纯物质对比态原理的计算方法用到混合物上。
.A .正确B .错误2. 对理想气体有A .()0/<∂∂T P H B. ()0/>∂∂T P H C. ()0/=∂∂T P H D. ()0/=∂∂P T H 3. 熵产生g S ∆是由于 而引起的。
A. 体系与环境之间的热量交换B. 体系与外界功的交换C. 体系内部的不可逆性D. 体系与外界的物质交换4. 以下4个偏导数中只有 是偏摩尔性质。
A .()jn nv ns i n nU ,,⎪⎪⎭⎫ ⎝⎛∂∂ B. ()j n p ns i n nH ,,⎪⎪⎭⎫ ⎝⎛∂∂ C. ()jnP T i n nG ,,⎪⎪⎭⎫ ⎝⎛∂∂ D. ()jnT nv i n nA ,,⎪⎪⎭⎫⎝⎛∂∂5. 分离过程的有效能损失,x L E ∆ 。
A. > 0B. < 0C. = 0D.可正可负6. 超临界流体是下列 条件下存在的物质A. 高于T C 和高于P C B .高于T C 和低于P C C .低于T C 和高于P C D .位于T C 和P C 点7. 纯流体在一定温度下,如压力低于该温度下的饱和蒸汽压,则此物质的状态为 。
A .饱和蒸汽 B.饱和液体 C .过冷液体 D.过热蒸汽8. 对理想溶液具有负偏差的体系中,各组分活度系数γi 。
A . >1 B. = 0 C. = 1 D. < 19. 气体经过稳流绝热过程,对外作功,如忽略动能和位能变化,无摩擦损失,则此过程气体焓值 。
A. 增加 B . 减少 C .不变 D. 不能确定10. 对同一朗肯循环装置,在绝热条件下如果提高汽轮机入口蒸汽压力,而温度等其余条件不变,则其热效率 。
溶液热力学性质的计算

=μi
9
注意化学位与偏摩尔性质的区别!
化学位的定义 偏摩尔性质的定义 它们的区别就在于下标!
10
化学位
偏摩尔性质
i
(nU [
ni
) ]nV
,nS ,n j i
i U i
U
i
[(nU ni
) ]T , P ,n j i
化学位:在V,S和其它组
偏摩尔内能:在T、P和其它
[(nU ni
) ]nV ,nS ,n j i
[
(nH ni
)
]P
,nS ,n j i
(nA) [ ni ]T ,nV ,n j i
[
(nG ni
)
]T
,P
,nj i
( 5
)
化学位的说明: 1. μi是状态函数,
强度性质 2. μi表示物质的逃
逸倾向和相变化或 化学变化的推动力。 变化方向高化学位 低化学位. 3.注意四个定义的重 点在于下标.
17
18
19
上式描述了偏摩尔性质之间的相互依赖关系, 它适用于均相系统中任何热力学函数M
20
Gibbs-Duhem方程
T,P一定 (xid M)i T,P 0
二元体系: x1d M1 x2d M 2 0
x(1 ddMx11) x(2 ddMx12) 0 x(1 ddMx11) x(2 ddMx22)
(nG)
d(nG) (nS)dT (nV )dP [ ni ]T ,P,nj i dni (4)
§4.1.3 化学位
定
义
化
学
位 i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K-Hessian方程的一个Liouville型结果
K-Hessian方程是一个非常重要的偏微分方程,它在几何分析和非线性偏微分方程理论中具有重要的应用。
在研究K-Hessian方程的解的性质时,Liouville型结果是非常关键的一个内容。
本文将介绍K-Hessian方程的基本概念和一些相关的Liouville型结果,并对其在数学和几何分析领域的重要性进行讨论。
1. K-Hessian方程的简介
K-Hessian方程是指具有如下形式的二阶非线性椭圆型偏微分方程:
\[ F(D^2 u) = f(x, u, Du) \]
\( D^2 u \)表示Hessian矩阵,\( f(x, u, Du) \)是一个给定的函数,\( F(D^2 u) \)是一个由Hessian矩阵的特征值和特征向量构成的函数。
当\( F \)具有特定的形式时,即可得到K-Hessian方程的特定形式。
K-Hessian方程广泛应用于几何分析、微分几何、非线性偏微分方程等领域,是一个非常活跃的研究方向。
2. Liouville型结果的概念
Liouville型结果是指对于某类特定的偏微分方程,如果其解满足一定的条件,那么这些解必然具有特定的形式。
一般来说,Liouville型结果是指对于椭圆型或拟线性椭圆型方程,在满足一定的增长条件或者衰减条件下,解的形式受到严格的限制,不能自由地增长或衰减。
Liouville型结果通常表明了方程解的全局性质,对于研究方程解的性质具有非常重要的意义。
目前,对于K-Hessian方程的Liouville型结果的研究已经取得了一些进展,但仍然有许多问题有待深入研究。
在K-Hessian方程的Liouville型结果的研究中,涉及到许多重要的数学工具和技术,包括凸几何、凸分析、局部和全局椭圆估计、梯度估计、Harnack不等式等。
通过这些数学工具和技术的运用,人们希望可以得到K-Hessian方程解的严格性质,这对于理解方程解的性质具有非常重要的意义。
